热-力-粘弹耦合多孔FGVM梁的动力学特性

周凤玺，蒲 育,2

(1.兰州理工大学土木工程学院，兰州730050；2.兰州工业学院土木工程学院，兰州730050)

功能梯度材料(FGM)梁因其可设计性、具有良好的热-机力学性能而被广泛应用于许多工程领域，如FGM 制备而成的梁式智能一体化传感器具有高灵敏度感知、适应环境强等优点、FGM 梁式人造骨骼等器官，具有极好的生物相容性和良好的柔韧性、FGM支撑构件用于核反应堆第一壁结构可以有效地克服高温环境中的热应力集中等问题。分析FGM 梁服役于特定工况时的静动态力学特性关乎结构的安全与设计、功能与优化，因而一直备受学者们关注和重视，目前已取得了丰硕的研究成果。

例如，基于Euler 梁理论(CBT)，Pradhan 等[1]采用微分求积法(DQM)数值研究了双参数Winkler-Pasternak 变弹性地基FGM 夹层梁的热弹性自由振动问题。赵凤群和王忠民[2]应用小波微分求积法(WDQ)数值研究了热载荷和切向随从力共同作用下FGM 梁的振动特性及稳定性。Mahi等[3]考虑了材料物性随温度变化的相关性，推导得出了材料物性关于几何中面对称FGM 梁自由振动响应的精确解。文献[4]采用Reddy 三阶剪切梁理论(TBT)，应用Ritz 法分析了均匀升温FGM 梁的热振动及热屈曲问题。同样采用TBT，Trinh 等[5]应用状态空间法(SSM)数值研究了热载荷和初始轴向力共同作用下多因素对FGM 梁振动及屈曲特性的影响。文献[6-9]均考虑了几何非线性因素，先后采用不同的数值分析方法研究了FGM梁的热后屈曲以及非线性振动问题。张靖华等[10]则应用辛方法分析了FGM 梁受热冲击时的动力屈曲特性。最近，蒲育和周凤玺[11]采用n阶广义梁理论(GBT)并提出一种改进型广义微分求积法(MGDQ)数值研究了3种典型边界FGM梁的热-力耦合振动特性和稳定性。文献[12- 14]则仅针对简支边界梁采用Navier 法求解其静动态输出响应，Ebrahimi 等[12]分析了多孔FGM梁的热-力耦合振动特性。文献[13- 14]在两类位移场描述法下基于GBT，探讨了多因素对湿-热-力耦合作用下FGM 梁振动特性和稳定性的影响。Zahedinejad[15]则分析了弹性地基FGM 梁在热环境中的自由振动特性。最近，蒲育等[16]基于二元耦联性解耦并应用MGDQ法数值研究了多孔FGM梁的热-力耦合振动和屈曲特性。文献[17- 18]基于CBT 并采用复数解法分析了FGM微梁的热弹性阻尼问题。综上所述，目前针对多孔功能梯度粘弹性材料(FGVM)梁的力学行为，尤其是动力学特性的研究鲜有文献报道。

本文从能量耗散角度出发，采用Kelvin-Voigt模型描述多孔功能梯度材料的粘弹性，提出三参数Winkler-Pasternak 粘弹性地基上多孔FGVM 梁模型，采用GBT 并应用Hamilton 原理建立热-力-粘弹耦合作用下FGVM梁的动力学控制方程，应用广义Navier 法求解该复杂耦合系统的有阻尼自由振动响应。通过算例，着重分析了梁理论、边界条件、热-力耦合效应、地基粘性外阻尼系数、地基弹性刚度、材料结构的内阻尼、孔隙率、梯度指标、跨厚比、振型阶次等诸多参数对多孔FGVM梁有阻尼自由振动频率特性的影响。

1 动力学控制微分方程

1.1 多孔FGVM梁模型及材料属性描述

如图1所示为Winkler-Pasternak 三参数粘弹性地基上内含均匀孔隙的功能梯度粘弹性材料(FGVM)梁，其几何尺寸长、宽、高分别为L×b×h，xoy为几何中面，梁的上表面为纯陶瓷材料，下表面为纯金属材料。假设梁两端受初始准静态轴向机械力为N(压力为正)，横向动载荷为q，粘弹性Winkler 地基刚度为kw，Pasternak 地基剪切刚度为kp，粘性外阻尼系数为cd，温度T沿梁厚度方向稳态分布，材料的物性依赖于温度变化且沿梁厚呈梯度连续分布。采用Kelvin-Voigt 模型表征功能梯度材料的粘弹性，设材料结构的内阻尼系数为cs，应用含孔隙率 γ修正后的Voigt 混合幂律模型，各物性参数(弹性模量E，泊松比ν，热膨胀系数 α，热传导率κ，密度 ρ)与坐标z及温度T可采用统一式表示为[13]：

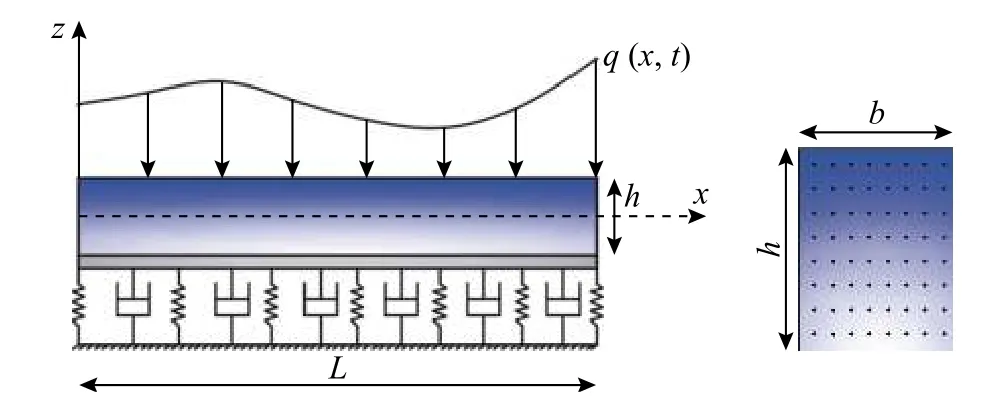
图1 三参数粘弹性地基上多孔FGVM 梁Fig.1 porous FGVM beam resting on three-parameterviscoelastic foundation

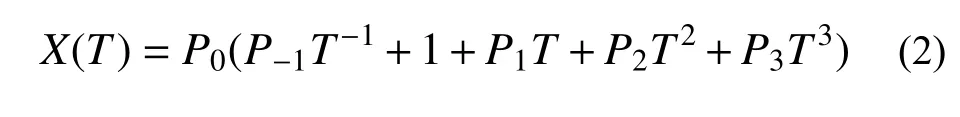
金属与陶瓷这两种材料的某一物性参数X随温度T的变化可统一表述为[13]：式中：Pi(i=-1,0,1,2,3)为随温度变化的材料系数。表1给出了金属(SUS 304)和陶瓷(Al2O3)这两种材料相应的温度相关系数[13]。

基于一维稳态热(传导方程：)

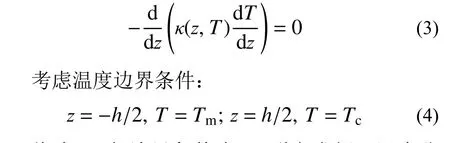
将式(3)与边界条件式(4)联立求解，温度分布T(z)可由热传导微分方程边值问题的定解给出[13]：

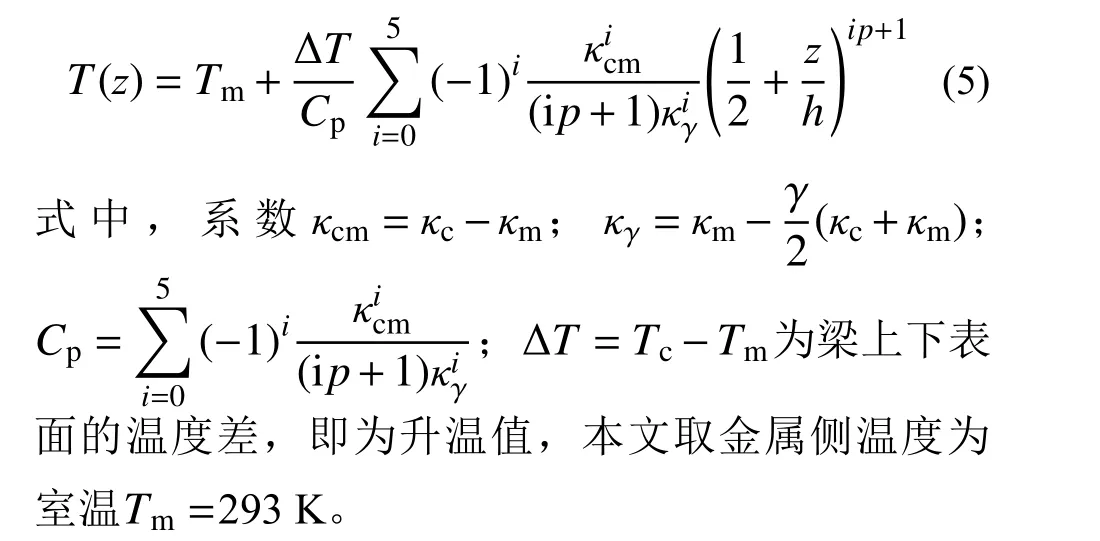
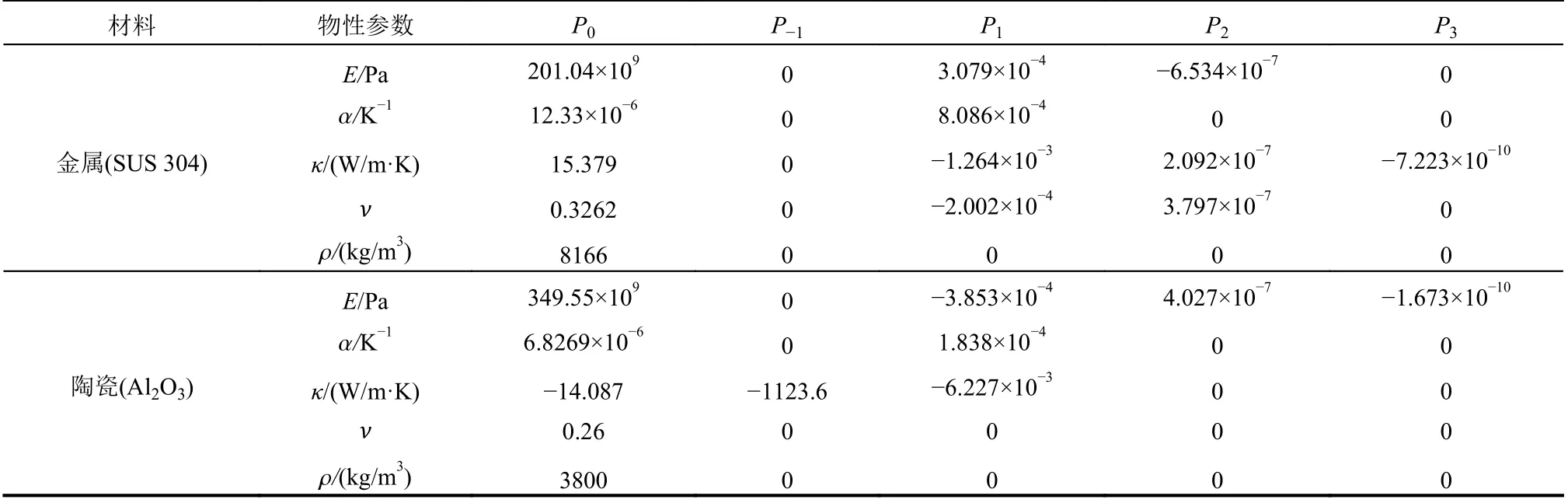
表1 金属(SUS 304)和陶瓷(Al2O3)两种材料随温度变化的物性系数[13]Table 1 Temperature-dependent coefficients for metal (SUS 304)and ceramic(Al2O3)

1.2 FGVM 梁的动力学方程

将式(6)～式(11)代入式(12)进行变分和积分运算化简后可得热-力-粘弹耦合多孔FGVM梁的动力学控制方程：

显然，动力学式(13)中存在热-力-黏弹载荷的耦合，弹性系数与惯性系数项中存在拉/压-剪切-弯曲变形的耦合。此外，式(13)中令动载荷q=0时，横向动载荷作用下结构的强迫振动方程则退化为有阻尼自由振动控制方程，下文将着重分析热-力-粘弹耦合作用下多孔FGVM 梁的自由振动问题。

1.3 多孔FGVM梁的有阻尼自由振动控制方程

考虑梁结构的自由振动，位移分量可设为：

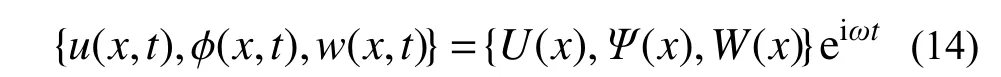
令动载荷q=0时，将式(14)代入式(13)化简后可得热-力-粘弹耦合多孔FGVM 梁的有阻尼自由振动控制微分方程：

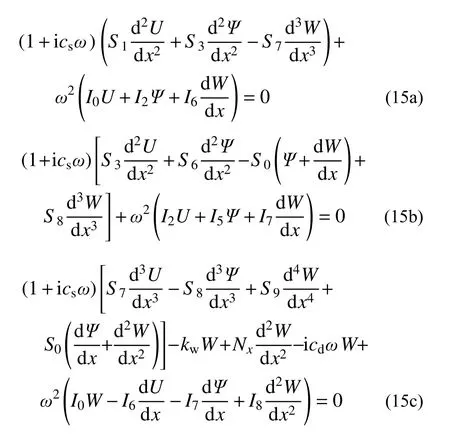
2 广义Navier 解析法

考虑以下3种典型梁边界：

(ⅰ)两端固支(C-C)

显然，控制方程式(15)与边界条件式(16)～式(18)联立后便描述了不同典型边界多孔FGVM梁在热-力-粘弹耦合作用下的自由振动问题。

2004 年，Elishakoff[19]，Reddy[20]在他们的著作中提出一种非平凡解析解用于典型边界复合材料梁板结构的静动态响应求解，该方法类似于Navier 法求解简支边界梁板结构的静动态响应，其实质仍是位移级数法求解，但它扩大了典型边界下获得梁板结构静动态响应解析解的使用范围，因此称其为广义Navier 法。

应用广义Navier 法[19-20]，梁轴线上任意一点的位移分量可由级数表示为：

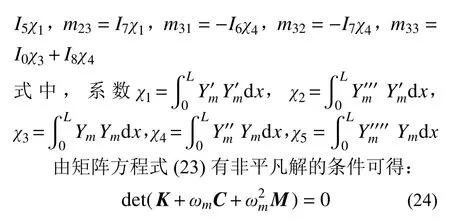
显然，求解式(24)可获得热-力-粘弹耦合多孔FGVM梁的有阻尼自由振动响应。

不失一般性，各参数采用如下的无量纲化形式：

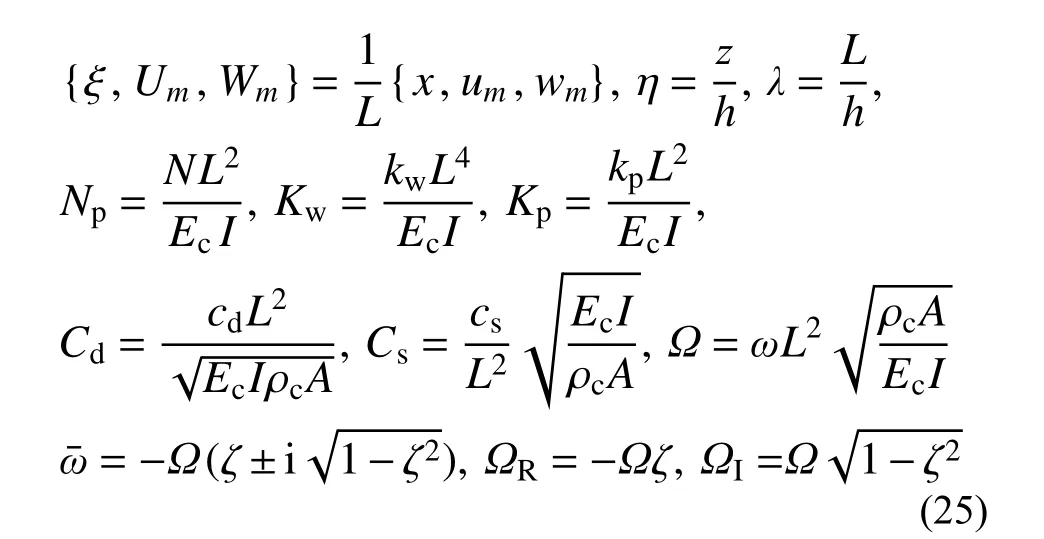
式中：Cd为无量纲粘性外阻尼系数；Cs为材料结构的无量纲内阻尼系数；Np为无量纲轴向机械力； Ω为无阻尼自振的无量纲频率；ω¯为无量纲特征复频率， ΩR和 ΩI分别为ω¯的实部和虚部； ζ为阻尼比；λ为梁的跨厚比；I为惯性矩。

根据以上所采用的无量纲频率定义式(25)，不难看出：无量纲特征复频率的实部 ΩR为负数，它反映了阻尼对位移输出响应衰减特性的影响。当0 ＜ζ ＜1时，复频率的虚部 ΩI表示欠阻尼自振频率；ζ =1则为临界阻尼；ζ ＞1则为过阻尼的情况。

3 算例与讨论

3.1 n阶GBT对FGVM梁欠阻尼振动特性的影响

本小节主要探讨GBT 阶数n对多孔FGVM 梁欠阻尼自由振动特性的影响。显然，GBT 可退化为常见的3种梁理论：取n=1，GBT 退化为Euler梁理论(CBT)；取n=3，退化为Reddy 三阶剪切梁理论(TBT)；取n=∞，则退化为Timoshenko一阶剪切梁理论(FSBT)。

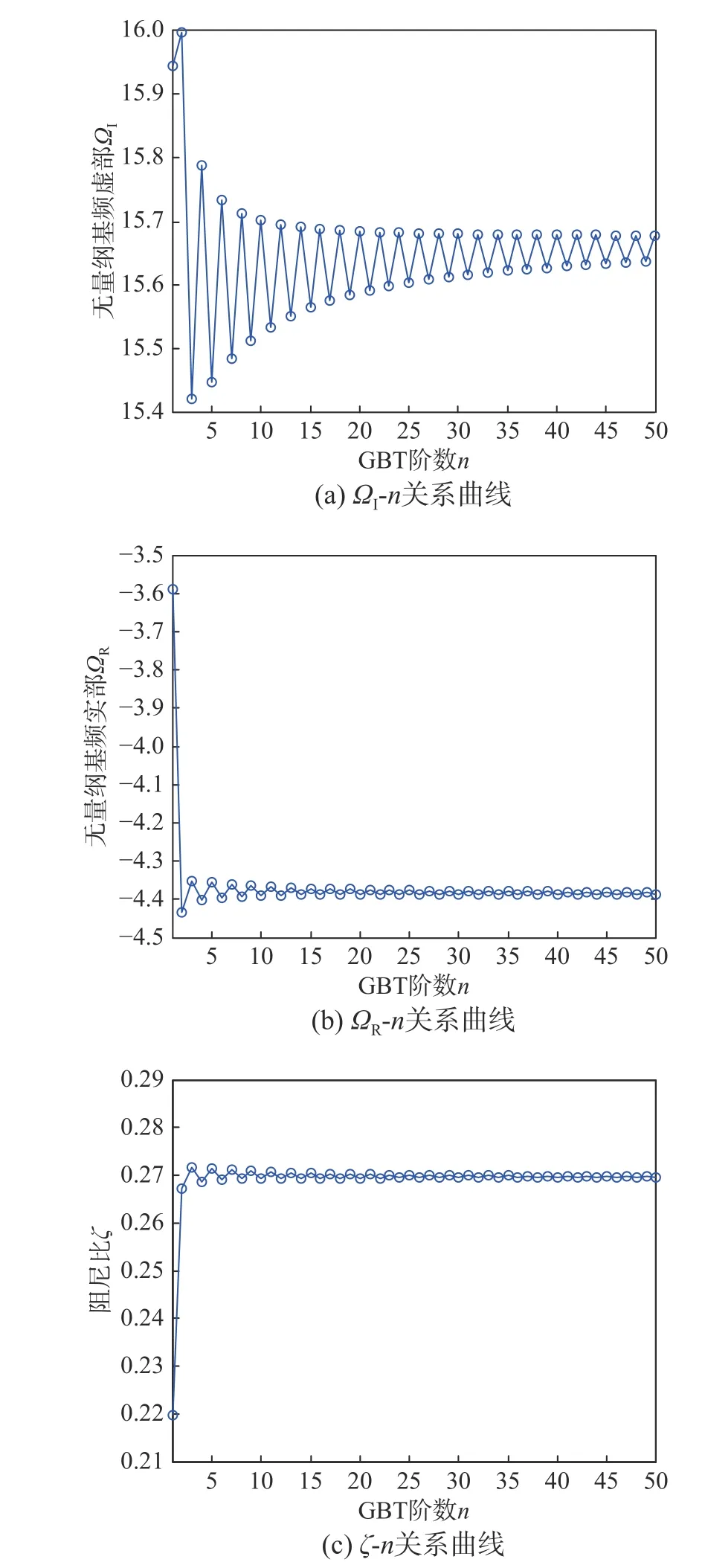
图2 多孔FGVM 固支梁的无量纲基频及阻尼比随GBT阶数n的变化关系曲线Fig.2 The dimensionless fundamental frequency and damping ratio of C-Cporous FGVM beam versusorder n for GBT

图2(a)～图2(c)分别给出了多孔FGVM固支短梁在热-粘弹耦合作用下其欠阻尼振动的无量纲特征基频虚部ΩI、实部ΩR及阻尼比 ζ随GBT 阶数n变化的关系曲线，其中取参数：p=1,λ=5,ΔT=200 K,γ=0.1,Kw=50,Kp=5,Cd=10,Cs=0.01。计算结果表明：n=1时，ΩI=15.944 13，ΩR=-3.589 03，ζ=0.219 60；n=2 时，ΩI=15.996 91，ΩR=-4.433 52，ζ=0.267 08；n=3 时，ΩI=15.422 80，ΩR=-4.352 11，ζ=0.271 58。由图2(a)来看：ΩI随正整数n的增大其变化波动较小且逐渐趋于稳定，直至趋于FSBT的预测值，且无需引入剪切修正系数。取n=2预测的ΩI值为最大，取n=3预测的ΩI值为最小，其极差为0.574 11。此外，CBT 相比于其它剪切梁理论(除n=2外)，CBT 预测的ΩI值偏高，与TBT 相比，其相对误差达3.38%。由图2(b)～图2(c)来看：除n=1以外，阶数n对ΩR和 ζ预测值的变化波动极小，相差无几，但CBT明显高估了ΩR，低估了 ζ值；CBT与TBT相比，其预测的ΩR和ζ值的相对误差分别可达17.53%和19.14%，其不容小觑。

综上所述，注意到算例中λ=5为短梁，CBT与TBT 及FSBT 相比，由于CBT忽略了剪切变形的作用影响，进而高估了短梁结构的刚度，因而CBT 高估了FGVM 短梁欠阻尼振动的频率ΩI值，即低估了衰减振动的周期；明显高估了ΩR值，进而明显高估了衰减振动的振幅；明显低估了阻尼比ζ值，进而明显高估了欠阻尼自振基频ΩI值。

3.2 其它因素对多孔FGVM 梁动力学特性的影响

本节均采用TBT，着重探讨热-力-粘弹耦合作用下多因素对多孔FGVM梁动力学特性的影响。

图3(a)～ 图3(c)分别反映了3种边界下多孔FGVM梁在热-粘弹耦合作用下其无量纲特征基频虚部ΩI、实部ΩR及阻尼比 ζ随无量纲外阻尼系数Cd变化的关系曲线，其中参数p=1,λ=20,ΔT=200 K,γ=0.1,Kw=25,Kp=5,Cs=0.01。由图3(a)可见：在欠阻尼状态，C-C、C-S和S-S这3种边界对应的各ΩI曲线值均随Cd的增大而单调减小，直至当Cd=Ccr达到各自临界阻尼状态时ΩI刚好为0，之后随着Cd的继续增加，FGVM 梁将进入过阻尼，此时ΩI保持不变恒为0，梁将不发生振动而变为纯衰减的运动，直至停止运动。此外，取相同的Cd值，边界约束越强，FGVM梁欠阻尼自振的频率越大，进而衰减振动的周期越小；达到各自临界阻尼状态时，C-C梁对应的Ccr=46.20为最大，S-S梁对应的Ccr=28.24为最小，C-S梁对应的Ccr=35.82则介于其间。

由图3(b)可见：当Cd＜Ccr在欠阻尼范围，3种边界梁的ΩR值均随Cd的增加而呈线性减小；同时注意到ΩR为一负值，这表明FGVM梁的欠阻尼振动为振幅减小的衰减运动；取相同的Cd值，S-S边界对应的ΩR值略微偏高，直线部分比较密集，这表明边界条件对振幅响应的影响较小。当Cd=Ccr达到各自的临界阻尼时，此时ΩI刚好为0，特征频率方程有2个相等的负实数根，即3种边界FGVM梁对应的临界阻尼Ccr为各自欠阻尼ΩR-Cd直线部分和相应过阻尼ΩR-Cd曲线部分交点的横坐标值。当Cd＞Ccr在过阻尼范围内，ΩI≡0，特征频率方程有2个不相等的负实数根，此时振动特性消失而变为纯衰减运动，ΩRCd为开口向右的关系曲线，且C-C边界开口较小、S-S边界开口较大，同时注意到3种边界对应的ΩR-Cd曲线明显疏离，这表明过阻尼时梁边界对位移输出响应影响十分显著。

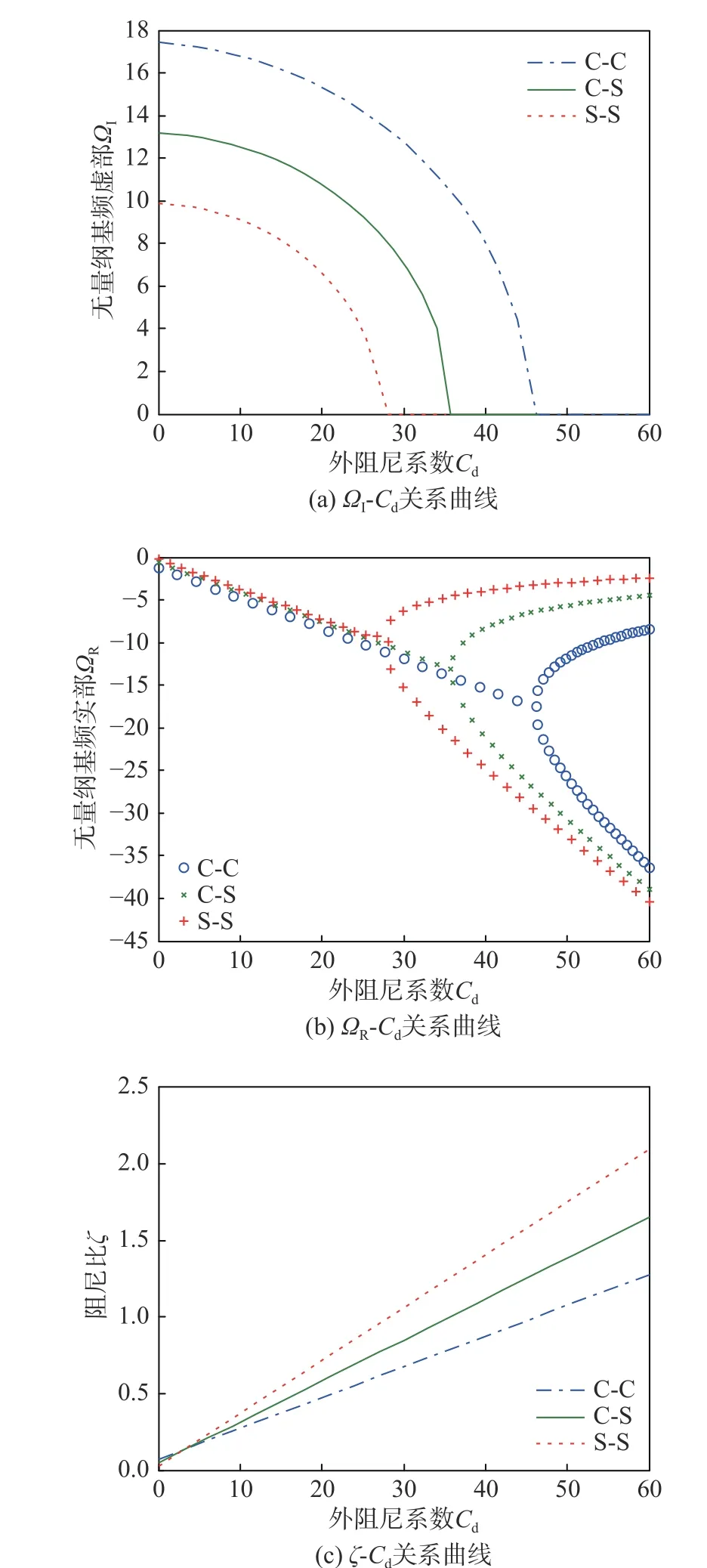
图3 无量纲基频和阻尼比随外阻尼系数的变化关系曲线Fig.3 Curves of dimensionlessfundamental frequency and damping ratio versus external damping coefficient

由图3(c)来看：3种边界FGVM 梁的阻尼比ζ随外阻尼系数Cd的增加而单调增大；当Cd＜5，边界条件对 ζ影响十分有限；当Cd＞10，取相同的Cd值，S-S边界对应的 ζ值明显偏高，C-C边界对应的 ζ值反而明显偏低，即简支梁具有高阻尼比，固支梁具有低阻尼比，C-S 梁则介于其间。

考虑了热-力-粘弹耦合作用，图4(a)～图4(c)分别刻画了多孔FGVM 固支梁的无量纲基频虚部ΩI、实部ΩR及阻尼比 ζ随外阻尼系数Cd变化的关系曲线，其中取参数p=1,λ=20,γ=0.1,Kw=20,Kp=2,Cs=0.01。由图4(a)来看：在欠阻尼范围内，取相同的Cd值，升温ΔT和初始轴向机械静载荷Np值越大，ΩI值反而越小，即频率ΩI随着热-力耦合效应的加剧而降低了；此外，当达到各自临界阻尼状态时，热-力耦合值越大，其临界阻尼Ccr值越小。这是由于升温ΔT值越高，热轴力就越大，且热轴力和初始轴向机械载荷均为压力，进而这两类载荷增大均削弱了FGVM梁结构的整体刚度。

由图4(b)来看：在Cd＜Ccr欠阻尼范围，ΩRCd直线部分十分密集，几乎重合，这表明热-力耦合效应对ΩR影响极其有限，即热-力耦合效应对FGVM梁欠阻尼振幅响应的影响几乎可以忽略；在Cd＞Ccr过阻尼的初始阶段，ΩR-Cd曲线部分明显疏离，这表明热-力耦合效应对纯衰减位移输出响应的影响十分显著，但随着Cd的持续增加(如Cd＞50)，ΩR-Cd曲线部分变的愈加密集，这表明热-力耦合效应在该阶段对位移响应的影响减弱，此时外阻尼对位移响应起主导影响因素。

由图4(c)来看：阻尼比 ζ随着Cd的增加而线性增大。当Cd＜ 5对于小阻尼， ζ-Cd关系曲线十分密集，表明热-力耦合效应对阻尼比影响极其有限；随着Cd的逐渐增大，取相同的Cd值，升温ΔT和机械力Np越大， ζ也越大，即阻尼比 ζ随着热-力耦合效应的加剧而增大。

结合图4(a)～图4(c)整体来看：对某一特定取值的热-力耦合载荷，3个子图均得出了与之对应相同的临界阻尼Ccr值。同时该算例也表明：对于小阻尼(如Cd＜5)，此时Cd对梁结构欠阻尼自振频率的影响甚微，在一般计算中，虽说是结构的有阻尼振动，但可以忽略阻尼对自振频率的影响，因而仍可使用无阻尼自振频率，与此同时，阻尼对振幅的影响则不容小觑，由于振幅按指数变化而迅速衰减，不久之后振幅将趋于零，使振动停止。

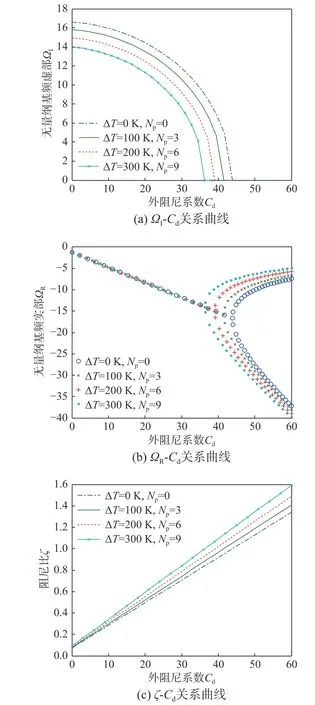
图4 热-力耦合载荷和外阻尼系数共同对多孔FGVM 固支梁无量纲基频和阻尼比的影响Fig.4 Effects of thermal-mechanical loads and external damping coefficient on dimensionless fundamental frequency and damping ratio of porous C-CFGVM beam

图5(a)～图5(b)分别反映了孔隙率和升温共同对FGVM固支梁的无量纲基频虚部ΩI和实部ΩR的影响关系曲线，其中取参数p=1,λ=20,Kw=50,Kp=5,Cd=10,Cs=0.01。由图5(a)可见：ΩI随着孔隙率γ 的增加而单调增大，即热环境中FGVM梁欠阻尼衰减振动的周期随着孔隙率的增加反而减小；取相同的γ 值，升温ΔT值越大，ΩI值反而越小，进而衰减振动的周期随ΔT的增加而增大。由图5(b)可见：ΩR随着孔隙率γ 的增加而单调减小，即振幅随着孔隙率的增加而显著衰减；由于5种升温取值所对应的各ΩR-γ 关系曲线十分密集，这表明升温ΔT对ΩR影响极小，即热效应对振幅衰减的影响十分有限。

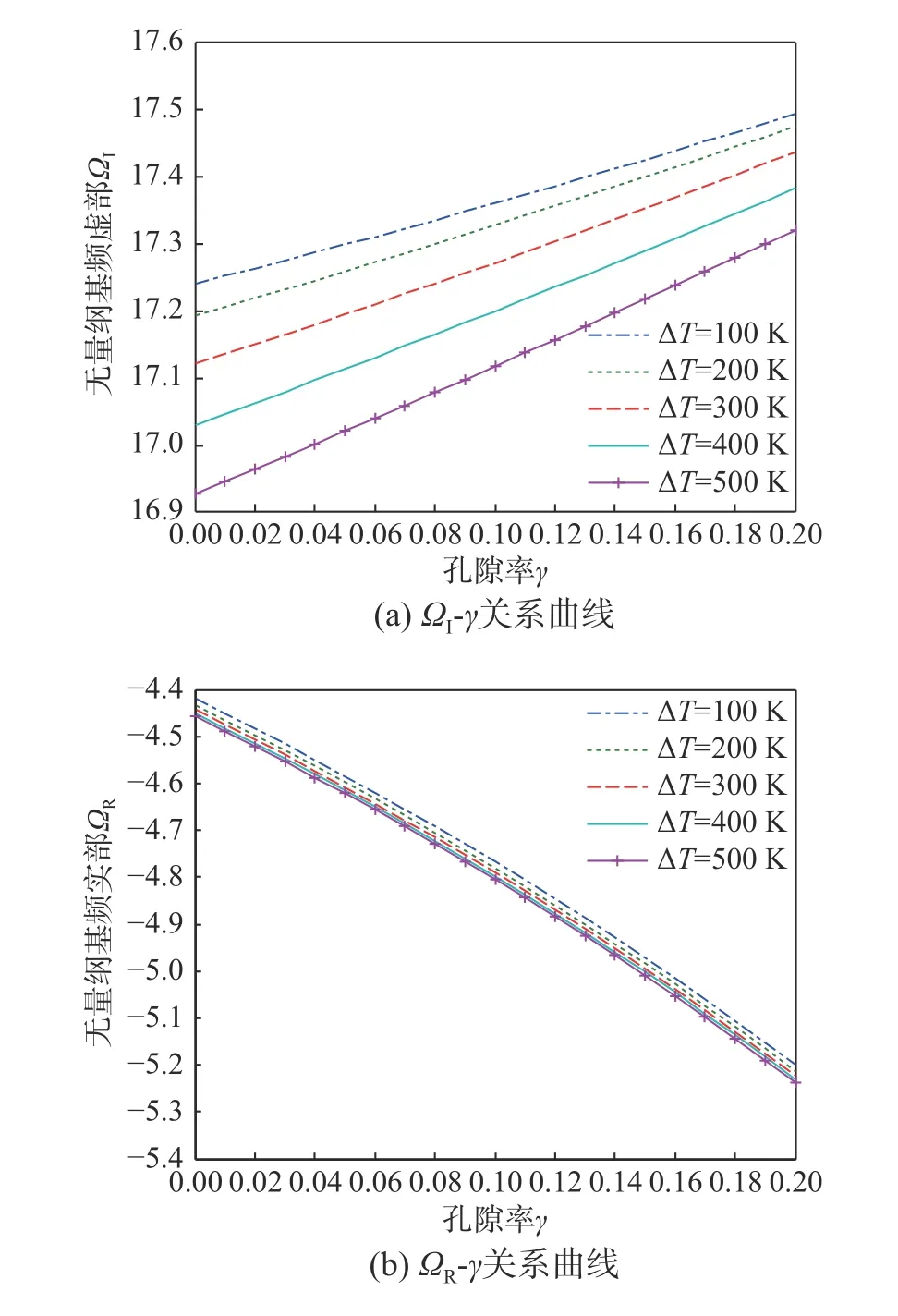
图5 孔隙率和升温共同对FGVM 固支梁无量纲基频虚部和实部的影响Fig.5 Effects of porosity and temperature rise on imaginary part and real part of dimensionless fundamental frequency for C-CFGVM beam

图6(a)～图6(b)分别反映了材料梯度指标p和结构的内阻尼系数Cs共同对多孔FGVM固支-简支(C-S)梁的无量纲基频虚部ΩI和实部ΩR的影响关系曲线，其中取参数λ=20,ΔT=200 K,γ=0.1,Kw=100,Kp=10,Cd=10。由图6(a)来看：基频ΩI随着p的增加而减小，在p=[0,2]范围内由于陶瓷材料Al2O3的组分体积含量骤减，梁结构的整体刚度显著降低，故而在此范围内ΩI减小最为明显，当p＞2以后，ΩI减小趋于缓慢；取相同的p值，FGVM梁结构的内阻尼系数Cs越大，ΩI反而越小，即ΩI随着Cs的增加而减小，其欠阻尼衰减振动的周期则随之而增大。由图6(b)来看：ΩR随着p的增加起先明显增大，当p＞2以后，ΩR增加趋于缓慢，换言之，欠阻尼振动的振幅随着金属材料SUS 304组份的逐渐增加起先明显增大，之后趋于缓慢；取相同的p值，Cs越大，ΩR值反而越小，进而欠阻尼振动的振幅随Cs的增加而迅速衰减，直至振幅减小为零而停止振动。

图6 材料梯度指标和内阻尼系数共同对多孔FGVM C-S梁无量纲基频虚部和实部的影响Fig.6 Effects of material graded index and internal damping coefficient on imaginary part and real part of dimensionless fundamental frequency for C-SFGVM beam

图7(a)～图7(b)分别反映了跨厚比λ和内外阻尼系数共同对多孔FGVM固支梁的无量纲基频虚部ΩI和实部ΩR的影响关系曲线，其中参数p=1,ΔT=300 K,γ=0.1,Kw=50,Kp=5。由图7(a)可见：基频虚部ΩI随着跨厚比λ的增加起先明显增大，之后随之而逐渐减小，特别地，当λ=[5,10]在短梁范围内，ΩI随着跨厚比λ的增加显著增大，进而衰减振动的周期随之而减小；取相同的λ值，内外阻尼系数越大，ΩI越小，即衰减振动周期随内外阻尼值的增加而增大。由图7(b)可见：基频实部ΩR随着λ的增加起先略有减小，当λ＞10以后，增加跨厚比λ对ΩR影响甚微，几乎无影响，换言之，FGVM长梁的跨厚比对欠阻尼振动振幅响应的影响可以忽略不计。

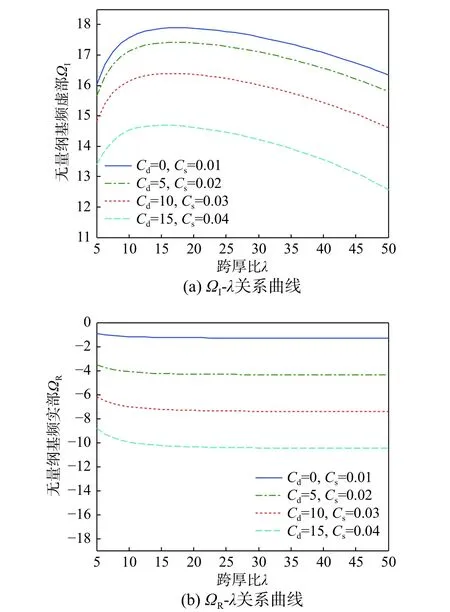
图7 跨厚比和阻尼系数共同对多孔FGVM 固支梁无量纲基频虚部和实部的影响Fig.7 Effectsof length-to-thicknessratio and damping coefficient on imaginary part and real part of dimensionless fundamental frequency for C-C FGVM beam

图8(a)～图8(b)分别刻画了Winkler 地基弹性刚度Kw以及Pasternak 地基剪切刚度Kp与内外阻尼系数共同对多孔FGVM固支-简支(C-S)梁的无量纲基频虚部ΩI的影响关系曲线，其中取参数p=1,λ=20,ΔT=200 K,γ=0.1，算例图8(a)中取Kp=5，图8(b)中取Kw=50。由图8(a)～图8(b)这2个子图总的来看：当内外阻尼不致于使FGVM梁越过临界阻尼状态时，欠阻尼自振基频ΩI都随Kw的增加而增大，ΩI也都随Kp的增加而增大，进而衰减振动的周期随地基弹性刚度的增加反而减小；特别地，当内外阻尼较大以致梁结构达到过阻尼而使ΩI≡0，如图8(a)～图8(b)中Cd=30，Cs=0.05所对应ΩI曲线的水平起始部分，但随着地基刚度的逐渐增加，FGVM梁之后的运动状态可由过阻尼转化为临界阻尼，直至达到欠阻尼。

图9(a)～图9(c)分别给出了C-C、C-S和S-S这3种边界下多孔FGVM 梁的前三阶无量纲频率虚部ΩI随内阻尼系数Cs变化的关系曲线，其中参数p=1,λ=20,γ=0.1,ΔT=200 K,Kw=50,Kp=5,Cd=10。总的来看：3种边界FGVM 梁的2阶和3阶频率ΩI均随结构内阻尼系数Cs的增加而明显单调减小，直至达到各自阶次的临界阻尼而使ΩI=0，随后进入过阻尼而使得ΩI≡0，且振动阶次越高，临界阻尼值越小，进而梁更易达到过阻尼而使位移输出响应迅速衰减。此外，边界约束越强，同一高阶次对应的临界阻尼值反而越小。特别注意到，3种边界FGVM 梁的基频ΩI均随着Cs的增加而略有减小。

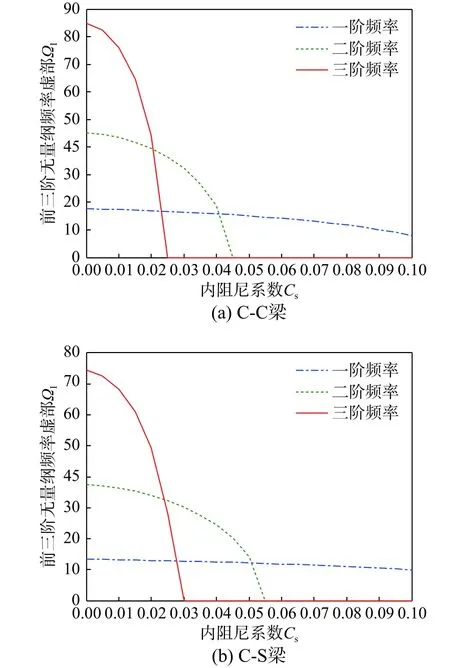
图8 地基弹性刚度和阻尼系数共同对多孔FGVM C-S梁无量纲基频虚部的影响Fig.8 Effects of foundation elastic parameters and damping coefficient on imaginary part of dimensionless fundamental frequency for C-SFGVM beam

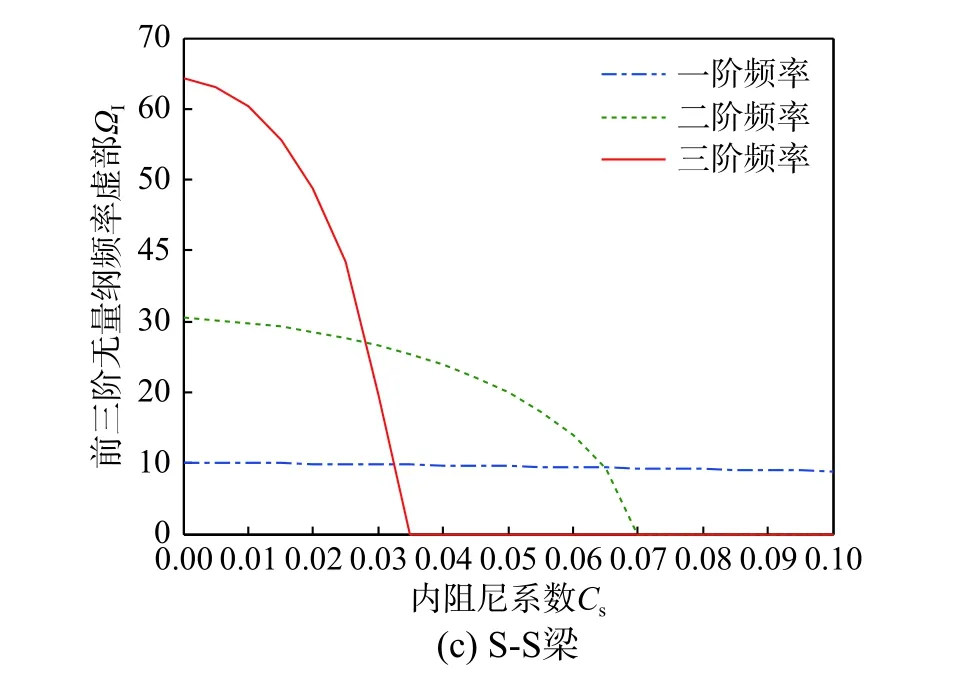
图9 前三阶无量纲频率虚部ΩI 与内阻尼系数C s 关系曲线Fig.9 Curves of imaginary parts of the first three dimensionless frequency ΩI versus internal damping coefficient C s

综上可知，结构内阻尼使得FGVM 梁高阶次的振动频率ΩI迅速减小，但对基频Ω1的影响较小，且振动阶次越高，梁结构更易达到过阻尼而使高阶次位移输出响应迅速衰减，换言之，高阶次的位移输出响应这时可忽略不计。

4 结论

采用n阶GBT，应用Hamilton 原理建立了3参数粘弹性地基上多孔FGVM 梁的动力学模型，应用广义Navier 法分析了热-力-粘弹耦合多孔FGVM梁的自由振动特性。结果表明：

(1)与TBT 和FSBT相比，CBT 低估了欠阻尼自振的周期；明显高估了衰减振动的振幅；明显低估了阻尼比。

(2)随着外阻尼的逐渐增大，FGVM梁经历欠阻尼、临界阻尼和过阻尼，其特征频率方程具有不同形式的复数根；C-C梁具有低阻尼比、高临界阻尼，S-S梁具有高阻尼比、低临界阻尼，C-S梁则介于其间。

(3)热-力-粘弹耦合FGVM 梁的欠阻尼自振频率随外阻尼、内阻尼、升温、热-力耦合载荷、梯度指标的增加而减小；但随孔隙率、粘弹性地基刚度的增加而增大；随跨厚比起先明显增大，之后单调减小。振幅随外阻尼、内阻尼、孔隙率的增加明显衰减；随梯度指标的增加起先明显增大，之后趋于缓慢；边界条件、升温、热-力耦合载荷、跨厚比对振幅响应的影响则比较有限。

(4)对于小阻尼，在一般计算中，可以忽略阻尼对自振频率的影响，与此同时，阻尼对振幅的影响则不容小觑，由于振幅按指数变化而迅速衰减，不久之后振幅将趋于零，使振动停止。

(5)当内外阻尼较大以致FGVM 梁结构进入过阻尼，这时可通过逐渐增加地基弹性刚度，可实现过阻尼到临界阻尼，直至欠阻尼之间的转化。

(6)振动阶次越高，FGVM 梁结构更易达到过阻尼而使高阶次位移输出响应迅速衰减，即高阶次的位移输出响应这时可忽略不计。