变拓扑混合双12脉波整流器的电流预测控制

2021-03-02张达敏张强曾汉超吕征宇

电机与控制学报 2021年1期

张达敏，张强，曾汉超，吕征宇

(1.厦门理工学院电气工程与自动化学院，福建厦门 361024；2.浙江大学电气工程学院，杭州 310027)

0 引言

随着电力电子及功率半导体技术的发展，电力电子装置在电力系统、工业现场的应用越来越广泛。AC-DC变换作为获取直流电能最基本的变换方式，在电力电子装置中作用重大。基于相控技术的功率二极管和晶闸管是上世纪六七十年代广泛使用的主流整流器件，在电路结构、可靠性、性价比、效率和鲁棒性上具有显著优势[1-2]。然而，相控整流器自身具有的低功率因数和高谐波电流的缺陷，使之应用范围受到限制，随着全控型器件的出现和性能的不断提升，在中小功率领域逐渐被全控型器件所取代[3]，然而大功率相控整流器仍广泛应用于直流电弧炉、等离子电弧炉、电解冶金、电动汽车充电站和高压直流输电等场合[4-6]。

为了抑制谐波污染和低功率因数，研究人员提出很多方法，总体而言，这些方法可分为两类[7-8]。其一，采用有源、无源或混合型电力滤波器。该方案虽然可以使网侧输入电流接近正弦波，但是电力滤波器的功率等级几乎接近整流器的功率等级，在谐波抑制的成本和电路损耗上没有优势[9]。其二，从谐波源着手，通过改造电力电子装置使其谐波下降或消失，如采用PWM(pulse width modulation)整流或多脉波整流技术。PWM整流器应用在大功率场合具有开关损耗大、效率低等不足，具有一定的局限性[10-12]。多脉波整流通过移相变压器产生若干组具有特定相位差的三相电源，同时给负载供电，依靠特定相位差的电流叠加来消除谐波，具有结构简单、成本低、效率和可靠性高、实现简单的优点[13]，如文[11-12,14]提出的基于二极管的多脉波整流器，然而，输出电压不可调限制了它在某些需要调压的场合的应用。对于多脉波相控整流器而言，当输入输出电压比值较大时，触发角较大(处于深控状态)，仅通过增加输出电压/电流的脉波数来提高网侧功率因数、抑制谐波电流的效果有限。因此，在输入电压不变的情况下，输出电压的范围将受到制约，难以适应负载需求。文献[15]提出柔性变拓扑概念，并将其应用于DC-DC变换器中，通过若干个投切开关的不同组合获得多种电路拓扑。文献[16]提出的变拓扑相控整流器只有2种工作模式：并联和串联。随着输出脉波数的增加，串联和并联输出的电压差值越来越大，导致串联工作模式的网侧功率因数下降。

针对上述问题，本文研究了一种变拓扑多脉波整流器(HDTPFTTR,hybrid double twelve-pulse flexible-topology thyristor rectifier)，通过改变拓扑结构尽可能缩小输入输出的电压差值，旨在降低网侧电流的谐波含量，同时，拓宽输出电压范围。采用电流预测控制策略控制整流器的输出电流，实现输出电流的快速响应。

1 HDTPFTTR工作模式分析

HDTPFTTR电路拓扑如图1所示。移相变压器输出4组相互隔离的交流电源(相位差为15°)，4组6脉波相控整流器与若干辅助开关组成一个拓扑结构可变的双12脉波整流器，开关状态的不同组合代表不同的工作模式。

图1 HDTPFTTR电路拓扑

与文献[16]相比，本文讨论的电路拓扑虽然只增加了2个开关(Sw9,Sw10)，但额外获得3种工作模式，尤其可贵的是获得了混合模式。混合模式工作时，4组整流器#1和#2、#3和#4先串联形成2个12脉波串联整流器，再并联输出24脉波，因此称为双12脉波整流器，其输出电压介于并联模式和串联模式之间。由于输入输出电压比下降，其网侧谐波电流含量小于串联模式，混合模式等效电路拓扑如图2所示。

图2 混合模式等效电路

除了输出24脉波的3种工作模式外，HDTPFTTR还能够工作于12脉波模式，等效为12脉波整流器，此时，只有2组整流器串联或并联工作，实现冗余设计。串联12脉波和并联12脉波各有2种等效电路，其等效电路对应的开关组合如表1所示。表中，1表示开关导通，0表示开关截止。

表1 开关状态与工作模式的关系

设定输入三相电压表达式如下：

(1)

并定义HDTPFTTR的输入电压矢量如下：

j=1,2,…,24。

(2)

式中：Ur为三相电源线电压有效值；vj代表输入的电压矢量。由图1及表1可知，双12脉波整流器工作于串联模式时，每个周期输出的电流为24脉波。因此，任意时刻其等效输入电压由4个相位差依次为15°的电压矢量合成，表达式如下

vjs=vj-1+vj+vj+1+vj+2。

(3)

式中vjs代表输入电压矢量的合成量。将式(2)代入式(3)中，得到下式

vjs=vj-1+vj+vj+1+vj+2=

j=1,2,…,24

(4)

其幅值如下式所示

(5)

再根据多脉波整流器的输出电压平均值与输入电压的关系，得到HDTPFTTR最大输出电压平均值如下式所示

5.17Urcosα。

(6)

式中：α为晶闸管触发角；U24ser为串联模式工作时整流器的等效输入电压幅值；Ud24ser为对应的输出电压平均值最大值。

同理，对于HDTPFTTR工作于混合模式，其输出电压的理论最大值与12脉串联模式工作时的输出电压理论最大值相同。任意时刻的等效输入电压矢量由2个电压矢量合成，如下式所示

vjs=vj+vj+1=

j=1,2,…,12。

(7)

因此，等效输入电压幅值与相应的整流输出电压平均值分别如下式所示：

(8)

2.61Urcosα。

(9)

式中：U24hyb为混合模式时整流器的等效输入电压幅值；Ud24hyb为相应的直流侧输出电压平均值。

2 电流预测控制实现

传统的多脉波整流器一般采用PI控制策略，其控制结构如图3所示。负载电流经低通滤波器后与给定的参考电流比较，输出的电流误差经PI控制器调节后传递给反余弦变换器，得到相应的触发角度；相位同步电路始终跟踪交流侧电压相位，最后根据触发角的大小调节晶闸管的触发时刻，即可改变输出电流。

图3 PI控制结构示意图

由于负载电流和触发角的函数关系为非线性关系(解析式为超越方程)，通过线性化处理得到的传递函数，对信号模型的折中处理降低了动态性能；其次，触发角的调整过程中存在较大的时滞环节，PI参数整定时需要考虑足够的相角和幅值裕度才能保证系统稳定，使得控制器的增益和带宽均受限。因此，采用PI控制的多脉波整流器难以达到满意的电流动态响应速度。

电流预测控制具有算法简单易实现、电流响应速度快的优点，因此在非线性系统如电力电子变换器、电机驱动中得到广泛应用[17-19]。本文采用电流预测控制策略来预测晶闸管的触发时刻，不需要计算触发角，仅包含简单的迭代运算，因此非常适合用DSP(digital signal processor)来实现。算法的本质是通过提前计算电感的储能量来实现预测，其简要计算过程如图4所示。

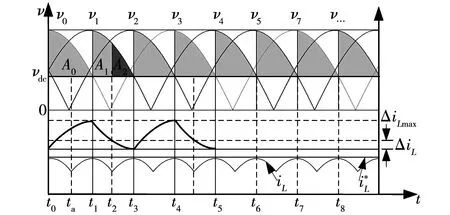
图4 电流预测控制原理图

从图4中交流电压和电感电流的稳态变化曲线可知，电感电流iL在交流电压和直流电压相交的时刻取得最大值，即此时电感的储能达到最大值，例如图中v0与vdc的交点对应的时刻t1，如果在此时刻触发v1，则施加于电感L上的电压差值(v1-vdc)的伏秒积分将使电感开始储能，电感电流上升，可以预测电感电流增量ΔiL将于v1-vdc=0的时刻(即t3时刻)达到最大值，记为ΔiLmax，满足

(10)

ΔiLmax是每个换相周期内电感电流能够获得的最大增量，实际上不是每个周期都需要最大增量(取决于负载电流参考值)，因此可以通过控制晶闸管的导通角来改变导通时刻，从而获得期望的电感电流增量。如果在(t1～t3)时段内的某个时刻(例如t2时刻)触发晶闸管，那么时刻的电感电流iL(t3)由可由式(11)～式(13)确定，实现了在时刻t2预测t3时刻的电流值。同理，其他时刻的电感电流值如iL(t4)、iL(t5)、iL(t6)等亦可被预测。

(11)

式中：

(12)

进一步，式(11)可化为

(13)

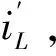
图5 电感电流增量图解

(14)

同时，脉动电流最大值ΔIm和t2,t3,t4分别由下式确定；

(15)

(16)

根据式(14)～式(16)，即可确定电感值的大小。而电感两端电压瞬时值uL(t)由输入和输出电压决定，即

uL(t)=vjs(t)-vdc。

(17)

式中：输入电压vjs(t)为HDTPFTTR输入电压的合成矢量，其大小与工作模式有关，不同工作模式对应不同的输入电压矢量。例如，在24脉波串联模式时，vjs(t)由式(3)决定。相应地，每个中断周期内控制器需要计算的电压矢量个数也决定于工作模式。

对于24脉波串联工作模式，每个中断周期需要计算24个电压矢量，其合成关系如式(4)所示；对于混合工作模式，24个电压合成矢量可通过下式求得：

vjs(t)=vj(t)+vj+1(t)=

j=1,2,…,24。

(18)

对于并联模式，输出电流不论是12脉波还是24脉波，其电压矢量均可表示为

j=1,2,…,N。

(19)

式中：N=12或N=24。

根据工作模式，分别计算该模式下每个电压矢量对应的电感电流瞬时值，当该瞬时值与参考电流相等时，即满足以下关系，

(20)

那么产生iL(tn)的电压矢量所对应的晶闸管将在下一个中断周期被触发导通，从而实现电流预测控制。

3 仿真与实验分析

为了测试HDTPFTTR基于电流预测控制策略的电流动态响应性能，利用MATLAB仿真平台分别搭建了HDTPFTTR基于电流预测控制和基于PI控制的仿真模型，选取蓄电池作为负载，仿真和实验参数设置如表2所示。

表2 仿真与实验参数配置

3.1 电流预测控制仿真分析

图6所示为HDTPFTTR工作于混合模式，以标称电流(120 A)对蓄电池充电的电压和电流波形。图示在恒流作用下电池端电压缓慢上升，电压纹波非常小(<0.1 V)，电流为24脉波，纹波为1 A。电池模型来源于国产某电动汽车蓄电池，容量为60 kWh，标称电压为500 V，初始容量为50%，初始电压494 V。HDTPFTTR工作于串联和并联模式的电压、电流响应与混合模式类似，所不同的只是网侧输入电流的谐波含量。

图6 混合模式工况的负载电压和电流

HDTPFTTR具有5种等效工作拓扑，图7、图8分别为HDTPFTTR工作于串联12脉波和串联24脉波的电流动态响应波形，由图可见，当参考电流阶跃突变时(120～80 A或100～80 A)，采用电流预测控制策略，负载电流可以平滑过渡，并且负载电流能够快速跟随参考电流。HDTPFTTR工作于其他模式的电流动态响应结果类似，不赘述。

图7 串联12脉波模式工作的电流动态响应

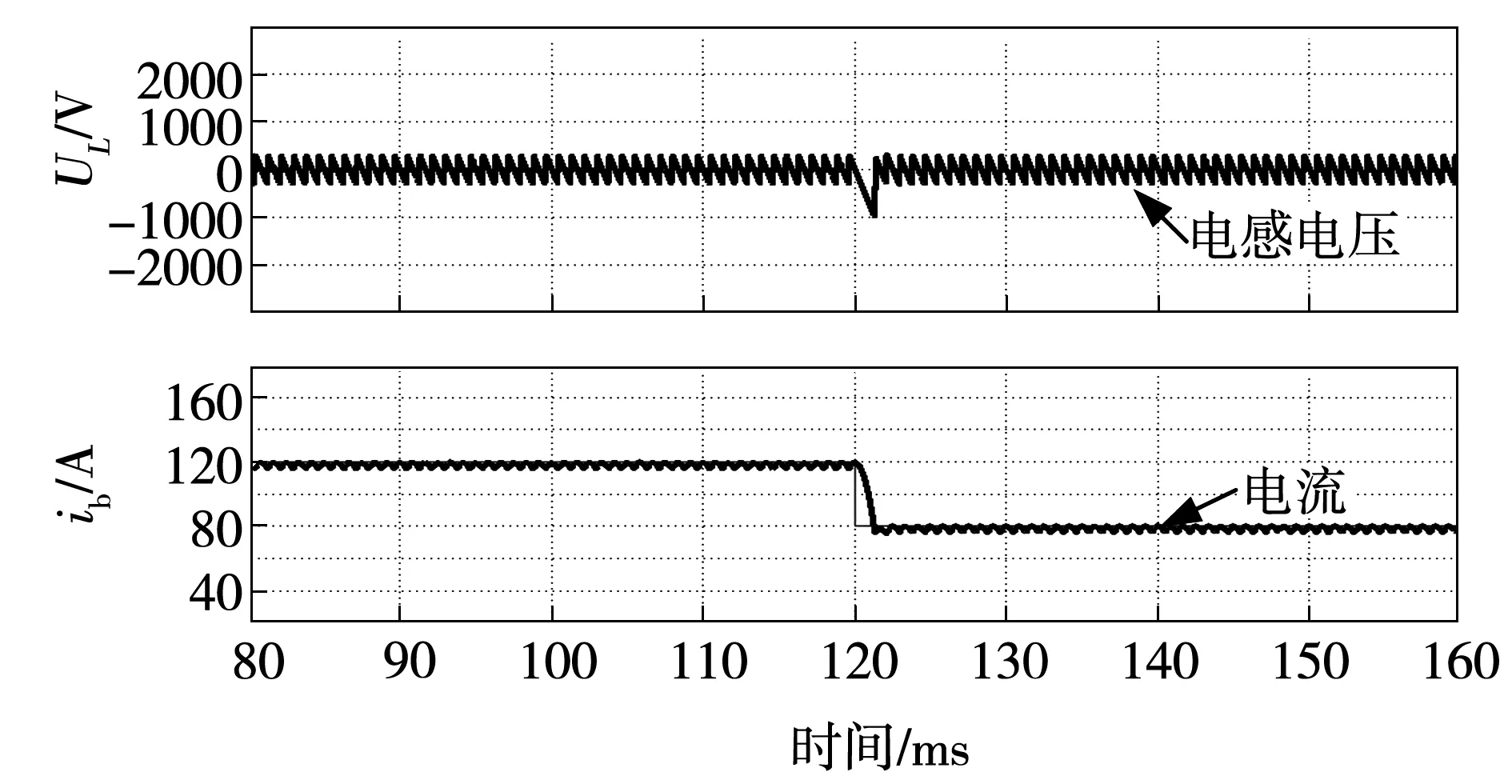
图8 串联24脉波模式工作的电流动态响应

图9～图11分别为HDTPFTTR在混合、并联12脉波和串联12脉波等工作模式间切换时的电流动态响应结果，此时负载电流为80 A。由图可见，得益于电流预测控制策略的快速响应，并且由于仿真模型中元器件设置为理想参数，因此HDTPFTTR在不同工作模式间切换时，负载电流能够平滑过渡。

对于图9、图10所示电感电压，由于混合模式和并联12脉波所对应的电压矢量不同，每个脉波所占的电角度也不同(混合模式为15°，并联12脉波为30°)，导致混合模式的电感伏秒积分大于并联12脉波模式，切换瞬间存在电感能量的突变，因此电感两侧出现较大的电压突变；图11所示为混合模式切换到串联12脉波模式，由于两者的等效电压矢量相同，电感伏秒积分也相同，切换瞬间不存在能量突变，因此，切换过程中电感电压平滑过渡，无冲击。HDTPFTTR在其他工作模式间切换结果类似。

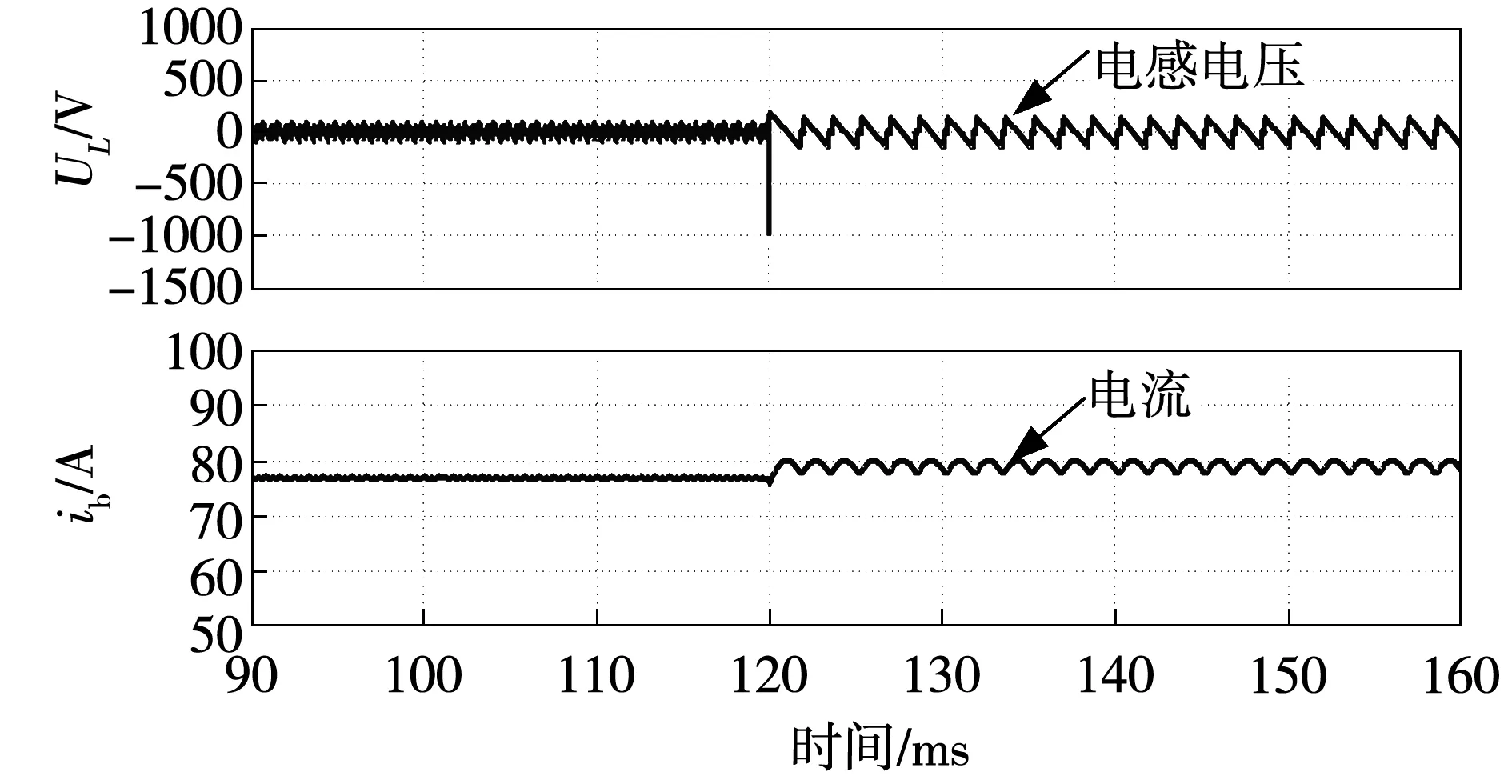
图9 混合模式切换到并联12脉波模式的电流响应

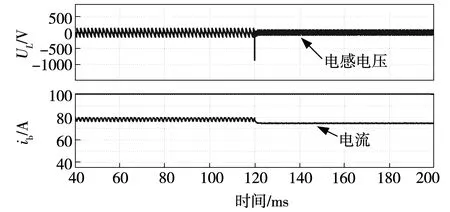
图10 并联12脉波模式切换到混合模式的电流响应

图11 混合模式切换到串联12脉波模式的电流响应

图12 串联12脉波切换到混合模式的电流响应

3.2 PI控制仿真分析

为了验证PI控制器的控制效果，根据图3所示控制原理框图搭建HDTPFTTR的仿真模型及其PI控制环路，分析不同工作模式下的电流阶跃响应，仿真结果如图13～图18所示。由图可见，采用PI控制策略，当电流给定值发生突变时，负载电流无法快速响应，需要经过1个周期(20 ms)以上的调整时间才能趋于稳定值，此外，电流超调量也比较大，如图18所示并联模式的电流超调量达到20%，同样工况下采用电流预测控制策略，其电流超调量仅为5%，并且仅需2个脉波(约1.67 ms)的时间即趋于稳定值，如图19所示。

图13 串联模式下的电流阶跃响应(80 A→100 A)

图14 串联模式下的电流阶跃响应(100 A→80 A)

图15 混合模式下的电流阶跃响应(80 A→100 A)

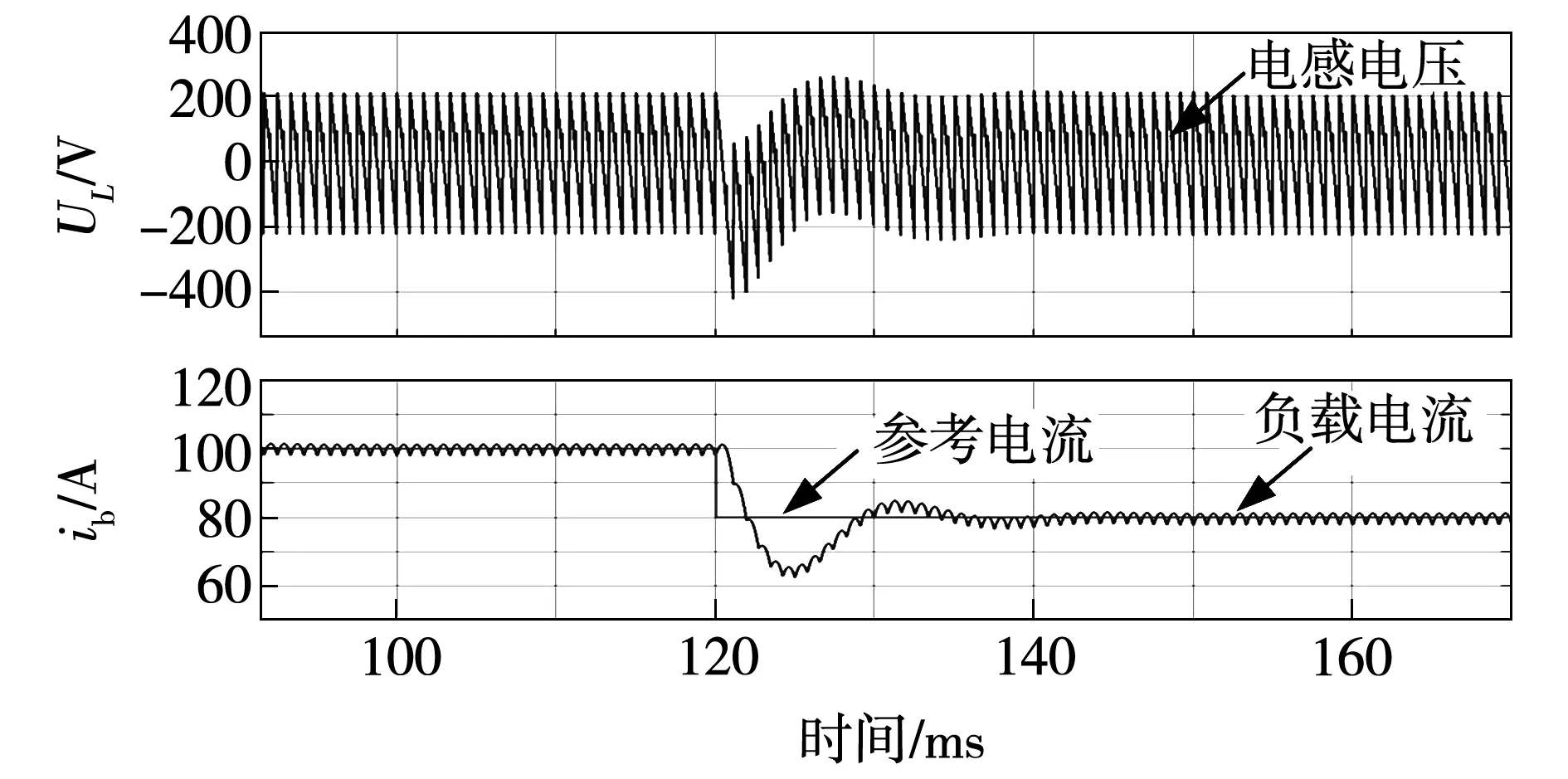
图16 混合模式下的电流阶跃响应(100 A→80 A)

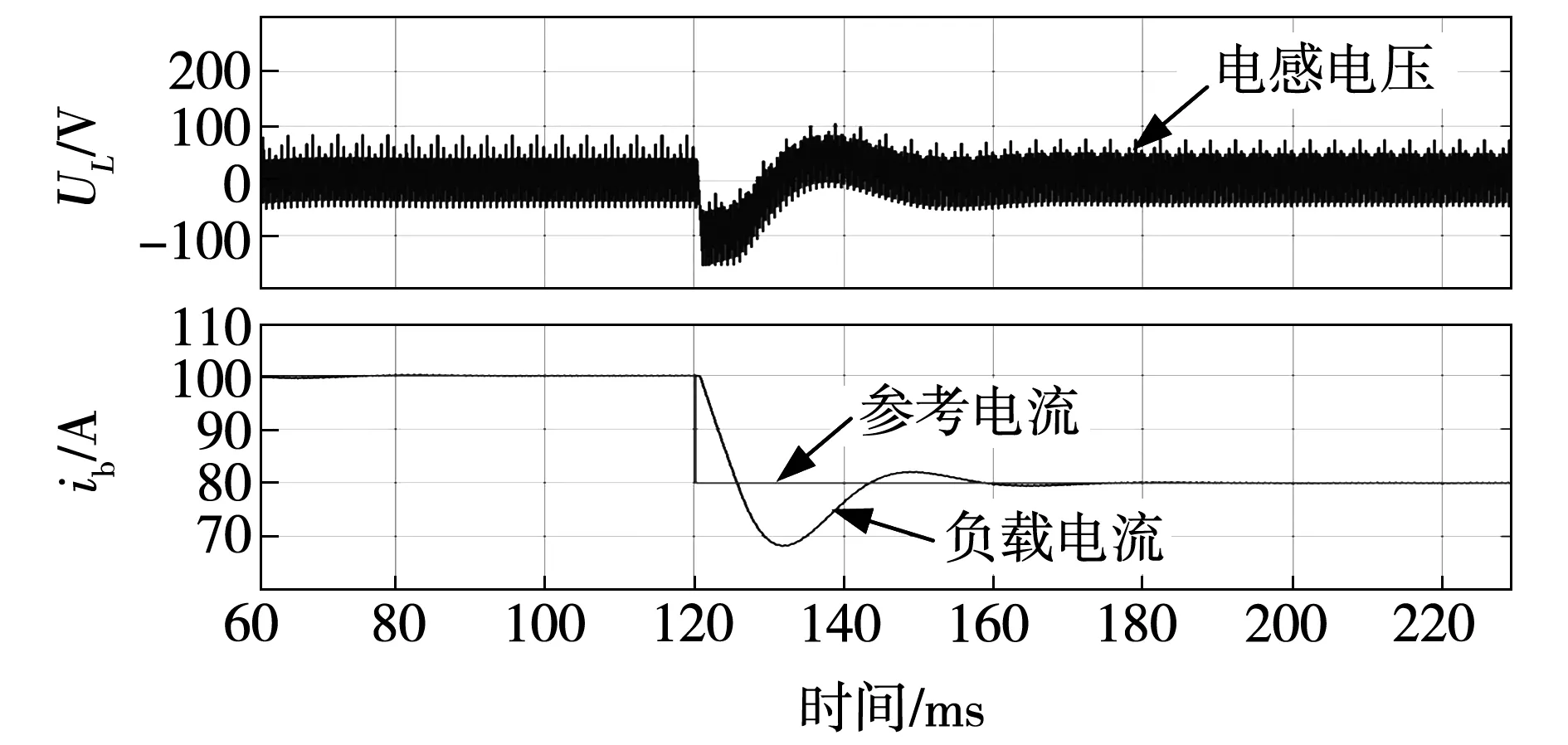
图17 并联模式下的电流阶跃响应(100 A→80 A)

图18 并联模式下的电流阶跃响应(80 A→100 A)

图19 基于电流预测控制的电流阶跃响应(80 A→100 A)

图20所示为电流阶跃响应时触发角的变化曲线，电流发生阶跃时，触发角发生较大幅值的变化，需要经过1个周期以上的时间才能趋于稳定。图21、图22所示分别为HDTPFTTR从串联24脉波模式切换至并联模式、混合模式切换至并联模式的电流响应曲线，仿真结果表明，基于PI控制策略，电流出现较大振荡，切换过程中电感电压峰值也远远大于电流预测控制工况(与图9、图10对比)。模式切换时的触发角变化曲线如图23所示，与电流阶跃响应类似，触发角也存在较大幅度振荡，需要20 ms以上的时间才能趋于稳定。其他模式之间的切换结果与此类似，不赘述。

图20 触发角变化曲线(100 A→80 A)

图21 串联模式切换至并联模式

图22 串联模式切换至混合模式

图23 模式切换时的触发角变化曲线

3.3 实验样机测试

为了进一步验证HDTPFTTR及电流预测控制策略的可行性，在仿真分析的基础上，搭建了一台3.5 kW的实验样机，如图24所示，电池负载由可编程直流电子负载(Chroma 63804)模拟，电流预测控制策略通过TMS320F2812数字控制器实现。4组交流电源由15°移相的Zigzag变压器输出。HDTPFTTR工作于混合模式，以恒定电流工作的负载电压和电流波形如图25所示。电压信号经电压霍尔传感器(HV03-10/25MA-P)输出端量测得到。图26为HDTPFTTR工作于混合模式的电流动态响应结果，电流切换期间无过冲，电流响应迅速，实验结果与仿真结果一致。图27和图28为HDTPFTTR在不同模式间切换的电流响应结果。实际电路中由于变压器存在漏感，电感电压突变造成负载电流存在过冲。优化移相变压器设计能够减小电流过冲。以实际的器件参数代入仿真模型中，将HDTPFTTR工作于混合模式时与常规的24脉波整流器工作于串联模式时的输入电流THD(total harmonic distortion)值对比，得到的仿真结果如图29所示。

图24 实验样机

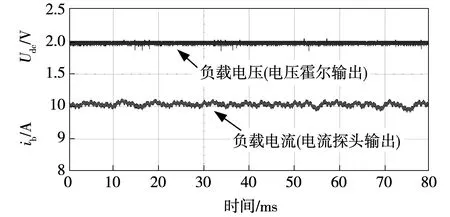
图25 混合模式的负载电压和电流波形

图26 负载电流动态响应(8 A→5 A)

图27 串联与混合工作模式切换

图28 不同工作模式间切换

图29 网侧输入电流THD值对比结果

由图29可见，混合模式下的输入电流THD显著小于24脉串联整流器。因此，在并联和串联模式之间引入混合模式，可以显著降低网侧输入电流的谐波含量(相对于串联模式)。当负载电流为120 A时，常规的24脉波串联整流器和HDTPFTTR工作于混合模式对应的网侧电流THD值依次为7.04%、2.44%。随着负载功率的增加，网侧输入电流的谐波含量将进一步降低，表明根据负载电压选取合适的工作模式(图示为混合模式)，可以显著降低输入电流THD值。将输入线电压设为380 V，负载电流100 A，并以实际的器件参数代入仿真模型，得到网侧输入电流的谐波分析结果如图30所示。图31所示为HDTPFTTR工作于混合模式和串联24脉波模式时的输入相电流仿真结果，电流波形进一步验证了图30的谐波分析结果。