基于图Laplacian的多机编队目标跟踪方法

张 毅,方国伟,杨秀霞

(1.海军航空大学航空作战勤务学院,山东 烟台 264001;2.海军航空大学岸防兵学院,山东 烟台 264001)

0 引 言

无人机(unmanned aerial vehicle,UAV)已日渐成为现代化战争中十分重要的装备[1]。UAV被应用于执行一些特殊任务,其中对地面或海面目标进行跟踪就是一项重要任务[2-4]。然而由于UAV自身机载传感器的限制和战场环境的复杂性,使得单架UAV的任务执行能力有限。因此,研究多无人机(multiple unmanned aerial vehicles,UAVs)协同执行任务成为了当前的热门问题。

对于UAVs协同目标跟踪问题,前期许多学者通过矢量场导引各UAV到预定轨道的方式实现了UAVs协同目标跟踪[5-7]。这种方法首先利用矢量场导引UAVs至目标周围的圆上,再控制各UAV间的相位差,实现UAVs对目标的协同跟踪。但该方法存在各UAV间的相位协同时间长,且对于跟踪目标速度有较大限制的问题。文献[6]更是明确指出被跟踪目标不得超过UAV速度的30%,当目标速度超过UAV速度30%时,就会导致UAV无法跟踪目标,显然这种情况无法满足实际的作战需求。针对上述问题,更多的学者将目光投向了通过编队对目标进行跟踪的方法,以克服矢量场导引方法的弊端[8-11]。

当前对于编队控制的研究主要有领导者-跟随者法[12-13]、虚拟结构法[14-15]、人工势场法[16-17]、基于行为法[18]以及一致性编队控制法[19-20]。无论采用何种编队控制思想,其根本目的都是使UAV编队能够生成并保持预期的编队队形进行飞行。然而在面对复杂作战环境以及不同任务条件时,编队往往需要处于时变的状态,即动态编队状态,以应对在飞行环境发生变化时能够视情况改变队形。因此,设计一个满足要求的编队控制器是保证UAV执行任务的关键。参照当前多智能体控制的研究现状,关于如何确定特定的编队队形主要有4种方法:基于绝对位置[21]、相对位置[22]、UAV间的距离[23]以及UAV间的方位[24]。可以发现，现有的4种确定编队形状的方法在旋转、平移和缩放3种简单运动下,编队的队形并非是不变的。例如，基于UAV间距离的编队队形控制方法,在旋转运动与平移运动下编队队形是不变的,但是在缩放运动下并不是不变的,因此编队队形控制的方法也是本文的一个重要内容。

文献[25]基于领导者-跟随者编队结构设计了编队目标跟踪制导律,通过设计领导者UAV的制导律,使得UAV编队实现对目标的跟踪,并克服了对被跟踪目标的速度限制。然而其虽实现了UAV间的相位协同,但各UAV仅仅与领导者UAV间相位协同,而非与目标间的相位协同,因此并不能达到对目标协同跟踪的目的。

综上所述,固定翼UAV编队协同目标跟踪的难点主要在于:① 如何在跟踪目标初期,在UAV满足飞行约束的情况下,设计一种能够实现动态编队飞行的控制方法,并使其具有更强的鲁棒性,以保证在遇到不同的飞行条件时,编队队形可精确变换;② 如何使UAV编队在目标跟踪过程中,实现UAV均匀分布在目标周围进行协同跟踪,使跟踪效果更佳;③ 如何克服对跟踪目标速度的限制。

本文采用基于UAV 3种运动方式的编队生成策略,提出了一种可随时间变化的UAV编队动态目标跟踪方法。首先在双积分模型的基础上,提出一种以旋转、平移和缩放3种运动为基础的UAV编队控制方法,设计了生成UAV编队的控制律,并给出了相应的稳定性证明;其次将编队控制的思想转化到UAV编队目标跟踪问题上,使各UAV能够保持相位协同并对目标进行跟踪;最后通过仿真,验证了本文设计的UAV编队目标跟踪算法的有效性。

1 问题描述

1.1 UAV模型建立

本文主要研究二维平面上的UAVs编队目标跟踪问题。设计UAVs二维质点运动模型为

(1)

为便于下文分析,此处将式(1)简化表述为

(2)

式中,pi=[xi,yi]T;ui(t)=[uix,uiy]T。

1.2 图论相关概念

定义有向图G=(V,ε),其中V为顶点的集合,ε为边的集合。若有向图的边(i,j)∈ε,则表示i能够传输信息至j,且称i是j的邻居,两者是邻接的。i的邻居集合可表示为Ni={j:(i,j)∈ε,j∈V,i≠j}。定义邻接矩阵A=[aij]∈RN×N,其中aij代表边(i,j)的权值,且

(3)

在有向图G中,分别定义顶点i的权值入度为

(4)

定义有向图G的Laplacian矩阵L∈RN×N为

L=[lij]=D-A

(5)

式中,D=diag{d1,d2,…,dN}∈RN×N为权值入度矩阵。

考虑到本文所建立的UAV模型中,UAV的状态是二维的,进一步定义邻接矩阵A=(Aij)∈RnN×nN,其中Aij=aijOij;Oij∈SO(2);SO(2)表示单位正交矩阵,定义为{Q∈Rn×n:det(Q)=1}。

2 编队控制方法

2.1 基于3种运动的编队控制方法

若要实现UAV编队对目标进行跟踪,首先需要对UAV编队的形成进行研究。为更好地描述UAV编队的控制问题,本文引入了两架虚拟UAV,作为UAV编队的参考量与基准量,分别记作UAVl和UAVb,定义UAVl的动态模型为

(6)

式中,pl=(xl,yl)T表示UAVl的位置;vl和ul分别为UAVl的速度与控制输入。

定义UAVb的动态模型为

(7)

需要注意的是,与UAVl不同,此处UAVb为编队的基准量,非实际意义的UAV,ub为预定参数,pb和vb受ub的控制,pb和vb在此处分别代表基准向量和基准变化向量,而不作为UAVb的位置与速度量。

假设 1UAVl和UAVb均至少存在一条到达所有UAVi的有向信息流,且各UAV之间关于UAVl和UAVb的信息传递是相同的，如图1所示。

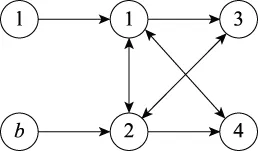
图1 编队通信拓扑示意图Fig.1 Formation communications topology

本文放弃采用以各UAV相对位置或相对方位的方法对编队队形进行描述,提出一种基于平移、缩放和旋转3种基本运动的编队控制方法。

为使UAV编队队形可以被唯一表示,此处构造编队参数组为

(pl(t),pb(t),r1(t),R1(t),r2(t)，R2(t),…,rN(t),RN(t))

(8)

式中,UAVi的平移运动由pl控制;缩放运动由缩放因子ri控制,且ri∈R,ri>0;旋转运动由旋转因子Ri控制,且Ri∈SO(2)。在3种运动中,UAV编队队形主要取决于ri与Ri控制,而编队移动主要取决于pl控制。为了简化表达,设编队因子为

Ci(t)=ri(t)Ri(t),i∈Θ

(9)

此时,式(8)可变换为

(pl(t),pb(t),C1(t),C2(t),…,CN(t))

(10)

以下给出基于3种运动的UAV编队控制问题的具体定义。

定义 1对于任意的初始状态,若满足:

(11)

则称通过式(10)实现了对UAV编队队形的控制。

本文考虑的缩放运动是UAVi以pb为基准,通过缩放因子ri进行控制;而旋转运动是指UAVi以pb为轴,旋转一定的角度,这也是将UAVb作为编队基准的原因。除此之外,定义1描述的是刚性编队,UAV编队的运动趋势取决于pl,可将其UAVl视作编队的虚拟长机。

为了更清晰地阐明定义1中所表述的控制意义,利用图2所示的编队控制示意图进行具体说明。

图2 编队控制示意图Fig.2 Formation control schematic

设编队的UAV数量N=4,采用图1所示的编队间通信拓扑关系。考虑pl是时变的,

显然,Ri∈SO(2)是满足条件的。此处设θ(t)=0,即pb=[0,1]T,可以发现,当pb确定后,编队中所有UAV将会沿着pb逆时针旋转角度θi,到达各自位置,说明UAV编队的队形可由式(10)控制形成。同时也说明,pb是可以时变的。

从这个例子中可以发现,即使pl是时变的,但pl并未对UAV编队的队形变化产生任何影响,而仅作为整个UAV编队的中心位置,控制编队运动轨迹。同时,更改pb的值对于编队队形的形状也不会产生影响,仅会导致编队相对于空间的位置发生变化。因此,UAVl与UAVb并不会对UAV编队队形产生影响。

如若考虑动态编队队形,则需控制Ri与ri为时变的,即控制θi与ri为时变的,ri的变化将使得UAVi与UAVl间的相对距离发生变化,即使得编队队形大小发生变化。

2.2 编队控制律设计

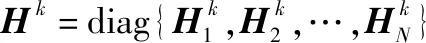
为了令编队能够在有限时间内实现编队队形,以下给出一种基于图Laplacian方法的编队控制律。

考虑到编队控制主要取决于编队中各UAV位置pi和速度vi,为此分别设计速度与位置控制律:

(12)

(13)

则UAV编队控制律为

ui=upi+uv i=χi-

(14)

此处在假设UAVl与UAVb均明确自身信息的前提下,给出估计值的状态更新律:

(15)

(16)

(17)

(18)

(19)

(20)

(21)

式中,⊗为Kroneckr积；Ml=L′+l;Mb=L′+

结合式(20)和式(21),可得式(16)～式(20)的表达形式:

(22)

(23)

(24)

(25)

(26)

式中,

给出定理1前,介绍本文所应用到的相关引理,便于后续证明。

引理 1[26]在假设1成立的前提下,满足:①Mk,k∈{l,b}是非奇异的;②Mk的所有特征根均有正实部;③M-1存在且为非负的;④ 存在正对角矩阵Q=[q1,q2,…,qN],使得QMk+(QMk)T是正定的且为严格对角的。

引理 2[27]考虑二次多项式

f(λ)=λ2+a1λ+a2

(27)

式中,a1与a2均为复数,则使f(λ)=0的所有特征根均具有负实部,当且仅当满足:

(28)

定理 1对于任意的

(29)

证明对于式(23),选取Lyapunov函数

(30)

对V1求导可得

(31)

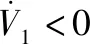
显然,存在正实数T1>0,使得t>T1时,el=0。

取T0=max{T1,T2,T3,T4},即存在T0>0,对于t>T0,el=ep=ev=eb=0。

证毕

将式(14)代入式(2),可得

(32)

式中,

M0=L+b⊗I2

C=diag{C1,C2,…,CN}

定理 2基于假设1和定理1,若满足:

(33)

(34)

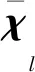
(35)

Al的特征多项式为

(36)

(37)

由于A为时变的,因此式(37)为线性时变系统。由文献[28]可知,当t≥T0时,

综上所述,式(14)可精准实现动态编队队形的控制。

证毕

值得注意的是,k1和k2数值大小的选择不仅与系统稳定性相关(满足式(33)的要求),而且与UAV编队的收敛速度也密切相关。

3 基于编队控制的目标跟踪算法

基于第2节编队队形控制的思想,本节对UAV编队目标跟踪问题进研究。

3.1 编队目标跟踪模型

当前按照UAV跟踪目标时的运动方式,主要将跟踪方式分为Standoff跟踪[5,29]与Persistent跟踪[30]。其中Persistent跟踪是使被跟踪对象持续保持在UAV传感器的有效观测范围内的一种方式;Standoff跟踪是UAV在目标周围保持定距盘旋跟踪的一种方式。两种跟踪方式主要区别在于是否存在盘旋运动。

从第2节的分析中可知,通过引入两架虚拟UAVl与UAVb的概念,对编队控制设立了参考量与基准量,实现了对编队队形控制。UAVl作为整个编队的领导者,决定了整个编队的运动趋势,UAVb作为基准者,充当了整个编队队形控制的基准量。

基于第2节的编队控制思想,本节通过考虑以UAVl模拟追踪目标运动的方法,同时保留编队基准UAVb,最终形成以目标为中心的编队跟踪方法,从而将UAV编队目标跟踪问题转换为以目标为中心的UAV编队队形控制问题。UAVl模拟追踪目标运动示意图如图所示,为了更好地说明问题,此处以目标匀速直线运动为例进行描述,UAVl以

为运动方向不断逼近目标,在时刻4追踪上目标,之后保持与目标同步运动。

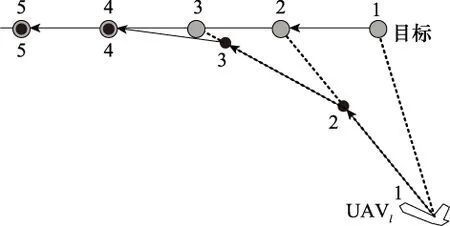
图3 UAVl模拟目标运动示意图Fig.3 UAVl simulates target motion

本文研究的是固定翼UAV编队对目标的跟踪问题,但由于固定翼UAV不同于旋翼UAV,其在飞行速度以及转弯半径上具有明确的约束,如下所示：

(38)

因此就必须要考虑到UAV编队目标跟踪期间的飞行情况[31]。其中,‖vmin‖、‖vmax‖、‖rmin‖分别代表固定翼UAV飞行速度的上下约束范围以及最小飞行转弯半径。

为了实现UAV对目标的持续跟踪,在考虑UAV与目标飞行速度vt关系的前提下,以下主要从UAV飞行速度约束层面,分两种情况对UAV编队目标跟踪问题进行了研究。

3.2 不同目标速度下的模型分析

3.2.1 ‖vt‖<‖vmin‖

为避免失速坠毁,UAV飞行速度不得小于最小飞行速度‖vmin‖。然而当目标运动速度‖vt‖<‖vmin‖时,此时若只考虑以时不变的UAV编队队形对目标实施跟踪,则UAV只能通过降低飞行速度‖vi‖保持跟踪,但这将可能导致UAV的失速坠毁。

针对这种情况,结合Standoff跟踪与编队控制方法,提出一种基于编队旋转因子Ci的UAV编队Standoff跟踪新方法。

考虑Standoff跟踪要求UAV与目标间保持一定的距离rs,并需在目标周围做持续盘旋运动,将这个问题转换为UAV编队队形控制问题式(11)上,即对编队因子Ci(t)进行讨论,根据式(9)分别对缩放因子ri(t)与旋转因子Ri(t)进行讨论。

对于ri(t)而言,其大小决定了编队队形的大小。在编队控制中，ri(t)控制了UAVi与UAVl的距离,而在此处ri(t)的大小决定了UAVi与目标间的距离rs的大小,考虑到rs是个定值,因此,此处仅考虑ri(t)为一个常值,即

ri(t)=rs/‖pb‖

(39)

由于‖vt‖<‖vmin‖,因此UAV需要在目标周围进行盘旋运动以保证UAV在不失速的前提下能够对目标进行持续跟踪。而对于Ri(t)而言,它控制了UAVi相对UAVb的旋转角度,而在Standoff跟踪问题上,UAV需要围绕着目标进行盘旋飞行,因此必须考虑Ri(t)为时变的,即θi(t)为时变的,此处令

(40)

式中,θi(t)=ωi(t-t0)+θ0i;ωi为UAVi的旋转角速度;θ0i为盘旋飞行前的角度;t0为盘旋运动的时刻。由于UAVi在目标周围保持匀速的圆周盘旋运动,因此这里考虑ωi为常值,使得θi(t)随时间线性变化,从而控制UAVi的盘旋运动是匀速的。

在UAV对目标进行Standoff跟踪期间,UAV主要包含对目标的盘旋运动与对目标的跟踪两个方面,因而考虑UAVi的速度为

(41)

为了保证‖vi‖≥‖vmin‖,则旋转角速度需满足

(42)

在式(10)的作用下,UAV编队可实现对目标的Standoff跟踪。

3.2.2 ‖vt‖≥‖vmin‖

当‖vmin‖≤‖vt‖≤‖vmax‖时,UAV对目标进行跟踪期间无需降低飞行速度,且‖vt‖在UAV速度约束范围内,此时设定UAV对目标跟踪期间仅保持编队飞行,不再进行盘旋运动,即此时仅需考虑UAV编队Persistent跟踪即可。

以下基于式(9)对编队因子Ci进行讨论。在‖vt‖≥‖vmin‖的情况下,对于缩放因子ri(t)而言,仅需满足:

0

(43)

式中,rc为UAV间的有效通信距离,即仅需保证UAV通信要求,ri(t)的取值不受过多约束。

与‖vt‖<‖vmin‖情况不同,一是由于编队不再需要在目标周围继续做盘旋运动,因而考虑旋转因子Ri(t)可以保持时不变状态,即θi∈R;二是考虑到编队中各UAV需保持均匀的相位,以实现对目标的协同跟踪,因此需要对各UAV的Ri进行前期约定,此处设定式(40)中的θi(t)为

(44)

即各架UAV均匀地保持在目标周围的圆形轨道上,实现协同目标跟踪。

值得注意的是,对于‖vt‖≥‖vmin‖的情况,实际上与编队队形控制无异,均是以时不变的编队队形实现对目标的持续跟踪。在式(10)的作用下,UAV编队可实现对目标的Persistent跟踪。

4 仿真验证

为了验证本文所提的编队控制方法和目标协同跟踪算法设计的合理性与有效性,本节令N=4,即利用4架UAV组成的编队为例,对在两种不同目标速度vt下的编队跟踪问题进行仿真验证,同时对不同取值的k1和k2对UAV编队性能影响进行仿真验证,以及对文献[6]的方法与本文所提的方法进行仿真对比。

仿真之初,对UAV与目标的初始状态进行设定。设定UAV的最小飞行速度为6 m/s,令4架UAV初始位置分别为(-500,0) m、(0,500) m、(0,-500) m和(500,0) m;初始速度vi为[20,0]Tm/s;UAVl的初始位置为4架UAV位置的中心点,速度为[20,0]Tm/s;目标初始位置为(200,200) m。同时设系统参数k1=3;k2=2;k3=k4=k5=k6=1;α1=α2=α3=α4=0.5;ri=200,i∈Θ;旋转因子R中参数θ=[π,π/2,3π/2,0];pb=[0,1]T。

4.1 情况1:‖vt‖<‖vmin‖时编队目标跟踪

设定目标速度vt为[4,4]Tm/s,由式(42)可得最小旋转角速度ωi=1/150 rad/s。‖vt‖<‖vmin‖时UAV编队目标跟踪如图4所示。

图4 ‖vt‖<‖vmin‖时UAV编队目标跟踪Fig.4 Target tracking when ‖vt‖<‖vmin‖

图4(a)展现了4架UAV从各自位置出发,在追踪目标的过程中生成圆形编队,随后保持编队飞行状态对目标实施追踪,在UAV编队追踪到目标后,由于目标速度‖vt‖未达到固定翼UAV最小飞行速度‖vmin‖,因此UAV编队在目标周围保持定距Standoff跟踪。图4(b)为UAV编队生成前后的误差ei=pi-pl-Cipb的图像,从图中可以发现,约在10.8 s时编队误差趋于0,这是UAV间已形成预期的编队状态;在19.7 s时误差曲线出现小幅抖动,但在24.4 s时误差重新趋于0,这是由于在19.7 s时,UAV编队已跟踪上目标,但由于目标速度较小使得UAV的速度不得不进行调整,这个误差是由于速度变化导致的,在24.4 s时UAV编队完成速度调整,误差重新为0。

4.2 情况2:‖vt‖≥‖vmin‖时编队目标跟踪

设定目标速度vt为[10,10]Tm/s,‖vt‖≥‖vmin‖时UAV编队目标跟踪如图5所示。

图5 ‖vt‖≥‖vmin‖时UAV编队目标跟踪Fig.5 Target tracking when ‖vt‖≥‖vmin‖

图5(a)展现了4架UAV以编队状态对目标实施跟踪的轨迹,由于目标速度‖vt‖大于固定翼UAV最小飞行速度‖vmin‖,因此UAV编队无需在目标周围进行盘旋飞行,仅需在目标周围保持相位对目标进行跟踪。图5(b)为UAV编队的误差‖ei‖图像,同‖vt‖<‖vmin‖一致,在10.8 s时,UAV间形成预期的编队队形,编队误差趋于0;在48.3 s时误差曲线出现小幅抖动,但在52.4 s时误差重新趋于0,这种情况同样是因为UAV的速度调整导致的。

4.3 不同k1和k2的影响

为了验证本文所提方法对于机动目标的跟踪效果以及不同数值的k1和k2选择对编队收敛速度的影响。此处令目标初始速度为[6,6]Tm/s;加速度为[4 cost,4 sint]Tm/s2;选择两组k1和k2参数值,分别为3和2,以及6和8,即令增加倍数κ为1.5;其余参数不变。

图6展示了在k1和k2取不同数值时UAV编队目标跟踪的情况,图6中，虚线为k1=3和k2=2时的仿真曲线,实线为k1=6和k2=8时的仿真曲线。从图6(a)可以看出,在两组参数下,UAV编队均实现了对机动目标的跟踪。从图6(b)可以看出，两组参数下的编队误差曲线变化,显然,在其他条件不变的情况,可以发现实线的收敛速度要快于虚线部分,也就是说增大k1和k2的数值将加快UAV编队的收敛速度,也验证了前文中对k1和k2数值大小的分析。

图6 不同k1和k2仿真对比图Fig.6 Comparison of different k1 and k2

4.4 仿真对比

图7 本文方法仿真结果图Fig.7 Simulation results of this method

比较图7与图8的仿真结果可以发现:① 由于文献[6]方法的局限性,使得UAV飞行速度被削减,导致跟踪上目标的时刻远远大于本文所给出的方法;② 本文的方法保证了UAVs相位快速协同,当编队跟踪上目标时就满足了相位协同的要求;而通过图5(b)和图8(c)可以发现,文献[6]则是在各UAV均跟踪上目标后,在Standoff跟踪圆上进行相位调整,导致实现UAVs对目标协同跟踪的整个过程耗时长。

图8 文献[6]方法仿真结果图Fig.8 Simulation results in method of [6]

综上分析可以得出:本文所提方法主要在两个方面表现出算法的优越性,一是满足了UAVs组成编队进行飞行的同时,各架UAV均能以目标为中心,实现对目标的协同跟踪观测;二是本文算法实现了协同跟踪速度快,用时短的优势。

5 结 论

本文针对平移、旋转和缩放3种基础运动形态,基于图Laplacian方法提出一种分布式固定翼UAV编队目标跟踪的方法。首先,基于3种运动形态提出一种由两架虚拟引导UAV的编队控制方法,通过设计UAV运动参数组来实现所需的特定编队队形,该方法能够满足动态编队队形变化需求,实际价值大。其次,通过考虑编队队形参数组的变化,结合UAV飞行约束条件,将编队控制方法应用于目标跟踪问题,成功克服了UAVs协同目标跟踪带来的协同时间长和跟踪目标速度受限的问题,并改善了UAV编队对目标的相位协同性问题。最后,通过仿真证实了本文方法的有效性和优势。值得一提的是,本文方法不仅能够应用于目标跟踪,同时也能够应用于编队避障、队形重构等问题,拓展研究价值大。

同时,本文在设计控制律的过程中假定UAV间信息传输不存在时间延迟的问题,因此下一步将考虑在时延情况下的UAV编队跟踪问题。