新型旋转抛物面换能器阵列的设计
2021-03-02谭笑枫李夕海曾小牛康志谦李广帅
谭笑枫,李夕海,曾小牛,康志谦,李广帅
(1.火箭军工程大学核工程学院,陕西 西安 710025;2.火箭军士官学校,山东 青州 262500)
0 引 言
从20世纪80年代开始,基于声参量效应的声频定向传输技术开始引起学术界的广泛关注[1-5]。因其具有一般扬声器不具备的高指向性和可控性等特点,在军事[6]、材料[7-11]、测量[12-13]、水声[6,14-15]、医疗[16]、成像[17]等领域都具有重要的研究意义和广阔的应用前景。在声频定向传输系统中,利用超声换能器组成的发射阵列是该系统的关键组成部分,对最终声波发射功率和指向性特点起着决定性的作用[1,18]。不少学者对于如何提高阵列的指向性进行了优化设计,但多针对于常规一维线阵、二维平面矩形阵和多边形阵[19-25]。无论是何种类型的平面阵列,都需要通过增加阵元数目的方法来提高指向性,造成换能器阵列成本上升;并且,为了避免栅瓣的出现,阵元间距必须控制在一定的范围,且该间距随着辐射声频的上升而缩小[26-27]。这显然与换能器自身的尺寸是一对难以调和的矛盾,在实际生产中难以兼顾,所以大大影响了声频定向传输的效果。本文在前人研究的基础之上,统筹考虑换能器阵元和点源阵列两者的指向性特点,构建了适用于任何几何形状排列的阵列指向性分析函数。在此基础上,设计了一种旋转抛物面式的曲面换能器阵列,并分析讨论了不同换能器个数、间距、抛物面焦距等参数对该阵列指向性的影响。
1 声场指向性理论
将描述一个声源发射或接收响应在远场区上的空间分布函数称为指向性函数,将其对应的函数图像称为指向性图。本文中关于声源指向性的推导皆基于下列条件[28]:
(1) 在没有特殊说明时,文中换能器和指向性均指发射换能器和发射响应所对应的指向性;
(2) 声源中心到观察点的距离远大于声源尺寸,即满足指向性函数中关于远场区的定义;
(3) 将声源中沿z轴向外发射的声波称作主波束,将其方向定为(0,0)方向。
1.1 单个阵元的指向性
在一个换能器的尺寸可与其所在介质中的声波波长相比拟时,其所辐射的声能将集中在某些方向上,这就说明该换能器具有指向性。对于单个换能器而言,其指向性取决于自身所发射的声波波长与尺寸的比[2]。将换能器看作一种平面状的振子,沿法线振动时其面上各点的振动速度幅值和相位都是相等的,也就是将单个换能器阵元等效为无限大障板上的圆形活塞声源(实际中只要障板的尺寸远大于声波在媒介中的波长,就可以认为是无限大障板)。
如图1所示,圆形的活塞换能器阵元置于xoy平面上,坐标原点选在阵元圆心处,阵元半径为r,定向面选在xoz平面,将该换能器阵元发射声波波长记为λ,频率记为f,根据文献[28]可知,其指向性函数D0(α,θ)可表达为
(1)
式中,J1(·)为一阶柱贝塞尔函数;k=2π/λ,为波数。声束与z轴的夹角记为θ;声束在xoy平面上的投影与x轴的夹角记为α。图2即为单个换能器声源的指向性示意图。从图2可以看出,其指向性同阵元的尺寸与波长的比值有关:随着活塞尺寸的增大或辐射频率的提高,声源的指向性越来越尖锐。

图1 无限大障板上圆形活塞声场示意图Fig.1 Sound field schematic diagram of circular piston on infinite baffle

图2 圆形的活塞换能器的指向特性Fig.2 Directional characteristics of circular piston transducer
1.2 阵列的指向性
对于发射阵列而言,阵列指向性的形成是由于其各个组成部分的阵元所发射的声波在远场中干涉叠加的结果。对于离散点声源组成的阵列,其在三维空间内的指向性函数Ds(α,θ)[28]为
(2)
式中,N为阵元数目;Δφn为阵列中第n个阵元沿任意方向(α,θ)发射的声波相对于其自身沿主瓣方向(0,0)发射声波的相位差,如图3所示;An为第n号阵元所产生响应的幅值,对于采用相同灵敏度阵元(即各阵元An相等)构成的阵列,式(2)可简化为
(3)

图3 任意阵列坐标分布示意图Fig.3 Diagram of coordinate distribution of arbitrary array
对于任意分布的各阵元,其位置用矢径rn=(xn,yn,zn)表示。在任意方向(α,θ),第n号阵元所辐射声波的单位矢量为
m=mxi+myj+mzk
(4)
根据图3中坐标的几何关系可以得到
(5)
同理,将该阵元沿主波束方向辐射声波的单位矢量记为
e=exi+eyj+ezk
(6)
主波束在(0,0)方向上,则
(7)
取坐标原点o为参考点,第n号阵元沿任意方向(α,θ)辐射的声波相对于o点的声程差ξi为
ξn=rnm=xnmx+ynmy+znmz
(8)
同理,第i号阵元沿主波束方向(0,0)辐射的声波相对于o点的声程差ξ0为
ξ0=rne=xnex+yney+znez
(9)
因此,第n号阵元沿任意方向辐射的声波相对于主波束方向的相位差Δφn为

(10)
式中,ω为角频率;c为声速。根据乘积定理[8],实际中阵列的指向性等效于阵元指向性与阵列本身(阵元为点声源)指向性的乘积。结合式(1)、式(3)和式(10)可知,只需要知道各阵元自身的基本参数和在阵列中的坐标位置,便可以完成对旋转阵列指向性D(α,θ)的计算:
D(α,θ)=D0(α,θ)Ds(α,θ)
(11)
1.3 指向性因数
为了更好地描述阵列指向性的性能优劣,本文引入指向性参数γ作为评价标准之一。γ表示对于一个具有指向性的声源,在主波束方向上对于远场中某点所辐射声能所占各个方向上声能的比。γ的计算公式为
(12)

2 旋转抛物面式的曲面阵列
2.1 阵列模型
首先,将超声换能器阵元组成常规平面阵列,作为该新型旋转抛物面阵列在平面xoy上的投影,然后根据旋转抛物面公式:
x2+y2=2pz
(13)
将其转化为焦距为p的旋转抛物面型阵列。此时,已经得到了阵列中所有阵元的参数和位置信息,即可根据式(11)对其指向性特点进行计算分析。
2.2 旋转抛物面型阵列指向性特点分析
按照上述方法,将100个同规格(发射频率为30 kHz,换能器直径10 mm)的换能器阵元按照各阵元圆心间距dx=dy=30 mm构造为一个10×10、焦距p=90 mm的旋转抛物面阵列,结果如图4所示。图4所构造阵列的二维和三维指向性图如图5所示。从图5可以看出,由于该旋转抛物面型阵列关于z轴对称。因此,无论定向面是xoz或yoz,阵列都拥有相同的二维指向性图。而且,此时绝大部分位置上的旁瓣能量都比主瓣低20 dB以上,说明该旋转抛物面型阵列对旁瓣干扰具有一定的抑制能力。下面分别就阵元个数N、阵列焦距p对γ的影响进行分析。如图6所示,当阵列其他条件保持不变时,该旋转抛物面型阵列的指向性因数γ总体上是随着N的增多而升高的,这与阵元数目对平面阵列指向性影响规律一致。然而γ与p并非呈线性关系,如图7所示,在p=140 mm时,γ取得最大值0.829。随着焦距的继续增加,抛物面逐渐演化并趋近于平面,自聚焦的优势开始丧失,γ随之下降;当p过小,弧面上所布设阵元互辐射干扰严重,γ急剧恶化。

图4 旋转抛物面型阵列的构造Fig.4 Structure of rotating paraboloid array

图5 旋转抛物面型阵列指向性Fig.5 Directivity of rotating paraboloid array

图6 阵元数目对指向性参数γ的影响Fig.6 Influence of array element number of directivity parameter γ
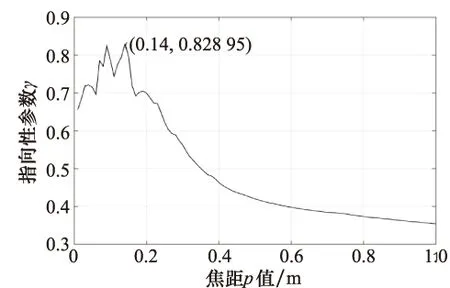
图7 阵列焦距对指向性参数γ的影响Fig.7 Influence of focal length array for directivity parameter γ
3 抛物面型阵列与常规平面型阵列对比
按照第2.2节的方法构造旋转抛物面型阵列,当p=140 mm时,计算此时的平面型阵列γ=0.263 7。两种阵列所对应的三维指向性如图8所示,二维指向性对比如图9所示。

图8 旋转抛物面型和平面型阵列的三维指向性Fig.8 Three dimensional directivity of rotating paraboloid and planar array

图9 两种阵列指向性对比Fig.9 Comparison of directivity of two arrays
从图8可以看出,同样的阵元间距,平面型阵列出现了较多的栅瓣,而本文所设计的旋转抛物面型阵列避免了这一情况的发生。对于分布在xoy平面上M×N的平面型阵列而言,消灭栅瓣的条件是
(14)
这就要求阵元间距必须控制在很小的范围内,并且该范围随着换能器发射频率的提高而缩小。对于上文中的常规平面阵列,换能器圆心间距必须小于或等于10.2 mm才能保证没有栅瓣的出现。但是,在实际应用中,换能器阵元的尺寸不得不考虑。常见的压电陶瓷换能器元件尺寸大都在10 mm左右,因此对换能器元件和阵列的加工工艺提出了很大的挑战。然而,阵元过于密集时,互辐射阻抗又会给阵列的指向性带来很大的危害[29]。对于旋转抛物面型阵列而言,这方面的要求就会宽松很多。如图9所示,当阵元间距为30 mm时,该旋转抛物面型阵列并未像平面型阵列一样出现栅瓣,且主瓣宽度未发生改变,指向性参数γ提高为平面阵列的3.14倍,仅在远离主瓣方位的±35°和±70°附近处,旁瓣级相较平面阵列有所提高。
在该旋转抛物面型阵列的基础之上,将阵元个数减少至81,其余条件不变。求得此时焦距p=90 mm时,指向性参数γ取得最大值0.721。将该阵列与阵元圆心间距为10 mm、排列为10×10的平面阵列进行指向性对比。如图10所示,在阵元数目用量减少的情况下,旋转抛物面型阵列相较于平面阵列,主瓣宽度减少16°左右,且对主瓣附近的旁瓣级抑制明显,在偏离主瓣±25°~±60°旁瓣级有所提高,平面阵列的γ=0.578 6。相比之下,旋转抛物面型阵列在减少19%阵元使用数量、扩大阵元间距的情况下,将提高指向性参数γ提高了24.61%。可见,旋转抛物面型阵列相较于常规的平面型阵列,主瓣更加尖锐,主瓣附近旁瓣级抑制明显,更有利于声波能量的集中。而且,换能器阵元使用数量更少,对阵元间距的要求更为宽松,降低了实际生产中的成本和难度。
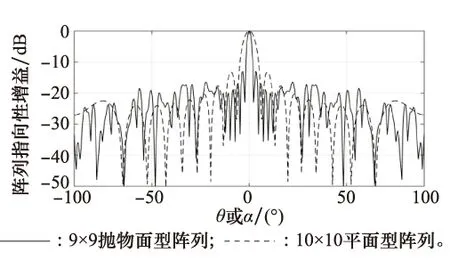
图10 阵元数目不等时两种阵列指向性对比Fig.10 Comparison of directivity of two arrays with different numbers of elements
4 结 论
本文基于阵列换能器指向性的原理,同时考虑了阵列构型和换能器阵元对指向性的影响,设计了一种新型的旋转抛物面型换能器阵列,提出了一种评价指向性优劣的参数,可基于此求得上述抛物面的最佳焦距。通过对比实验发现,该旋转抛物面型换能器阵列抑制旁瓣和栅瓣的能力更强,可以在主瓣方向获得更为集中的声能,且降低了在换能器数量和间距方面的要求,为新型声频定向传输系统的设计和创新提供了参考。
