基于小波域的图像超分辨率重建方法

董本志， 于明聪， 赵 鹏

(东北林业大学 信息与计算机工程学院，黑龙江 哈尔滨150040)

1 引 言

图像超分辨率重建[1](Super-Reconstruction，SR)是通过低分辨率 (Low Resolution, LR)图像或者图像序列恢复出高分辨率(High Resolution, HR)图像的技术，由Harris[2]等人在20世纪60年代首次提出，之后在卫星成像[3]、医学成像[4]、光学成像[5]、图像生成[6]、生物成像[7]等计算机视觉任务和图像处理领域均取得了突出成就。目前主流方法有基于插值、基于重构、基于学习3种。

基于插值和基于重构的方法对自然图像的先验知识具有较大的依赖性，从而导致处理复杂图像时无法恢复出更多的细节信息，重建能力有限。基于学习的方法通过建立高、低分辨率图像两者之间的映射关系，利用学习获得的先验知识来完成高分辨率图像的重建。目前基于学习的方法主要有基于稀疏表示、近邻嵌入和深度学习的方法。Timofte[8]等人将稀疏字典和领域嵌入进行结合，提出了锚定领域回归算法和改进后的锚定领域回归(A+)算法，计算效率得到了提高，但图像细节恢复效果较差。传统学习模型的特征提取和表达能力极其有限，很大程度上限制了重建效果，而基于深度学习的方法以其强大的学习能力在超分辨率领域得到了广泛的应用，重建效果相较于其他方法具有大幅提升。

基于深度学习的SR研究中，Dong[9]等人首次提出了基于卷积神经网络(CNN)的超分辨率图像重建方法SRCNN，通过端对端的训练学习来解决SR问题。SRCNN具有3个卷积层，分别代表图像块的特征提取、表示和重构，显著提高了传统方法的重构进度。但是该网络学习到的特征单一且感受野太小，缺乏语境信息，收敛速度慢，同时计算花销很大。随后FSRCNN[10]、ESPCN[11]等利用反卷积层以及亚像素卷积层替代SRCNN 模型中双三次插值的操作，有效减少了总计算复杂度，但是随着网络层数的加深，训练花销和构建难度逐渐增大。何凯明[12]于2015年提出的残差网络(Resnet)使网络深度大幅加深得以实现，在减少训练时间和加快收敛速度方面展现了较强的优势 。基于这一思想，Kim等人在SRCNN的基础上，提出了超分辨率重建深度网络[13](VDSR)和循环超分辨率神经网络[14](DRCN)。通过梯度裁剪、跳跃连接、递归监督等方法，降低了深度网络训练的难度。但是其输入图像需要进行双三次线性插值放大的预处理，会丢失低分辨率图像的原始信息，导致最终结果出现伪影问题。随后的基于残差网络的超分辨率模型，如DRNN[15]，LapSRN[16]，SRResNet[17]，DenseNet[18]等陆续被提出。然而上述模型都是通过单尺寸卷积模块的线性叠加实现网络纵向加深，以追求其更高的表达能力和抽象能力。然而伴随着网络的加深，从原始图像中提取到的浅层特征逐渐被淡化，在逐层卷积和过滤计算的过程中会出现结构信息丢失从而出现伪像。2018年Li[19]等人提出了双通道卷积神经网络，该网络通过特有的深、浅双通道提取特征信息，获取了更多原始图像信息，具有较好的重建效果。同年，Du[20]等人通过引入多尺度卷积滤波器竞争策略来增强网络的重建能力，可以自适应地选择图像重建信息的最优尺度，并在有限的计算资源下构建了浅层网络，扩展性较强，处理实际问题时效果很好。但是这两种算法仍不能充分利用原始图像信息的结构与细节信息。

小波变换具有多分辨率分析功能和逐步分解等特性，能够在图像重建过程中全面利用图像的结构与细节信息，使得超分辨率重建后的图像信息丰富且细节清晰。Bae[21]等人于2017年提出利用小波残差网络来进行图像超分辨率重建和图像去噪；相似地，Guo[22]等人提出一种基于小波变换的深度网络来恢复图像损失的细节，并取得了较好的结果。2018年，Liu[23]等人以U-NET[24]为网络基本架构，加入小波变换来进行图像超分辨率重建等任务。上述3种网络在小波域内重建效果可观，但仍然未能充分利用每一个卷积层的信息。

针对上述方法的不足，本文提出基于小波域的残差密集网络(WRDSR)。WRDSR以神经网络预测小波系数，将图像重建从低维到高维的映射过程转化为同等维度的预测，能够更有效地重建出清晰图像。同时，网络采用密集连接、跳跃连接以及特征融合来加强网络各层次的信息交流，防止了因激活层中线性整流函数(Rectified Linear Unit, ReLU)的截断效应导致信息在传递过程中出现丢失的现象[25]，更好地捕捉上下文之间的信息，最后通过亚像素卷积与小波逆变换进行图像重构，缓解棋盘效应，进而提高图像重建质量。

2 模型设计

基于小波域的残差密集网络模型(WRDSR)通过空域到小波域的变换来实现超分辨率图像的重建。为了更加有效地提取特征并降低运算的复杂度，网络直接将LR 图像的小波子带图像作为网络的输入，最终映射到HR图像的小波域下，共分为小波分解、特征提取和小波重建3个模块。首先，小波分解模块利用二维离散小波变换将低分辨率图像分解成4个不同频率的子带图像以分离结构与细节信息，使得后续网络能够对结构与细节分别进行最大程度的特征提取与留存。在特征提取过程中，模块采用残差密集网络对小波分解输出的4个LR小波子带图像实现特征提取。最后，小波重建模块将残差密集网络输出的特征图通过亚像素卷积生成4个对应的HR小波子带图像，经二维离散小波逆变换生成最终的HR图像。整体结构如图1所示。

图1 网络模型结构

2.1 小波分解

小波变换已被证明是一种高效的特征提取方法[26]。它可以充分表达和利用一张图像在不同水平上的上下文和纹理信息，二维离散小波变换(2DDWT)如图2所示。同时小波变换具有正交性，因而可将其应用到图像超分辨率重建中。

图2 二维离散小波变换

Huang等人[27]证明，图像的高频小波系数会随着其模糊程度的增加而逐渐消失，获得清晰SR图像的关键在于还原低频信息的同时也能还原高频小波系数。所以SR可以看作是恢复输入LR图像细节的问题，这可以与小波变换相结合，如果把变换后低频小波图像表示为LR 图像，那么其它的小波子带图像就是想要的重建图像易缺失的高频细节。WRDSR采用哈尔小波进行2DDWT，其具体步骤为：首先对图像的每一行进行1DDWT，获得原始图像在水平方向上的低频分量L和高频分量H；然后分别对L、H的每一列进行1DDWT，获得原始图像的水平和垂直低频分量LL、水平低频和垂直高频分量LH、水平高频和垂直低频分量HL以及对角线高频分量HH。输入的LR图像经过2DDWT得到4个小波子带图像LRWav，即：

LRWav={LLL,LLH,LHL,LHH}∶=2DDWT{LR}，

(1)

式中，LLL,LLH,LHL,LHH是LR图像生成的小波子带图像，分别对应低频分量、水平低频垂直高频分量、水平高频垂直低频分量和对角线高频分量，2DDWT{LR}表示对LR图像进行2DDWT操作。

2.2 特征提取

特征提取模块中的网络由密集连接块(Dense Block，DB)以及特征融合层组成，拥有4个输入通道，分别对应于2DDWT模块中输出的4个小波子带图像LLL,LLH,LHL,LHH，通过神经网络向前传播表示为一系列特征图。

首先，LRWav通过一个初始3×3的卷积层对4个输入进行浅层特征提取操作F1，得到浅层特征ILR：

ILR=F1(LRWav)

.

(2)

ILR随后进入由密集连接块组成的深度特征提取层，其中每个密集连接块内分别含有3个3×3用于提取特征的卷积层以及3个用于调整神经元的活跃度，增强网络的非线性的ReLU层。层与层之间采用密集连接，同时前一个DB的输出和每一层的输出直接连接到后一层，既保持了前馈的特性，又可以结合图像浅层低维特征(纹理、彩色、形状)和深层的高维语义特征生成质量更好的特征表示，减少了信息流在网络中传递的损失。随后在末端进行块内特征融合并通过1×1卷积层实现降维，得到每个DB块的特征图输出。DB结构如图3所示。

图3 DB结构

第i个DB输出fd表示为：

fd=(FDBi(FDBi-1(…FDB1(ILR)…)))，

(3)

式中，FDBi表示第i个DB的特征提取操作。

每个DB的输出，不仅作为下一个DB的输入，同时也输入到块外特征融合来充分利用原始图像中的分层特征，通过网络的不同域信息流保留尽可能多的特征，对最后特征融合层的输出利用1×1卷积层进行降维得到最终小波预测系数f(LRWav)：

f(LRWav)=Fconcat(f1,f2,…,fd)，

(4)

式中，Fconcat为特征融合操作，fd为第i个DB输出。为了整个深度网络训练的稳定性和特征提取的高效性，在DB块内以及整体特征提取模块中加入残差链接来避免梯度爆炸和梯度消失的问题。

2.3 小波系数重建损失

在相机成像过程中，由于硬件方面的限制，生成的图像上每个像素只代表附近的颜色，而在微观上，实际物理像素之间还存在许多像素，即亚像素。在SR过程中，无法被传感器检测出来的亚像素可以通过算法近似计算出来，相当于推理出图像缺失的纹理细节等高频信息。

WRDSR在提取了LR空间的特征后，采用亚像素卷积用于完成将非线性映射得到的高维小波特征图超分辨率重建成高分辨率小波深度图。假设目标倍数为r，输入的低分辨率特征图大小为H×W，将其与通道数为r2的H×W亚像素卷积核进行卷积，得到H×W×r2个像素值，再将其重新排列组合成大小为rH×rW的目标图像。上采样过程如图4所示。

图4 亚像素卷积

小波逆变换得到最终重建结果SR，即：

SR=2DIDWT{f(LRWav)}，

(5)

式中，2DIDWT{f(LRWav)}表示对f(LRWav)进行2DIDWT操作。

2.4 小波系数重建损失

神经网络训练过程是一个通过迭代不断降低损失值并得到最优解的过程。在图像空间常用的损失函数是对HR图像和SR图像逐像素进行均方误差操作，本文同样采取这种方式，不同之处在于对图像对应的小波系数进行这一操作。本文针对SR采用小波系数重建损失，标签为 HR图像的小波系数HRWav：

HRWav={HLL,HLH,HHL,HHH}∶=2DDWT{HR}，

(6)

式中，HLL,HLH,HHL,HHH分别对应低频分量、水平低频垂直高频分量、水平高频垂直低频分量和对角线高频分量的小波系数。

整体网络的损失函数为：

(7)

3 实 验

3.1 实验环境

实验硬件设备为PC：Intel(R)Core(TM)i7-6700 CPU@3.40 GHz处理器，4G运行内存，利用NVIDIA GeForce RTX 2080 Ti进行GPU加速。软件环境为window 10 系统下的Tensorflow机器学习框架。

3.2 实验数据及实验参数设置

实验数据分为训练集和测试集。训练集采用DIV2K数据集并通过水平、垂直方向反转以及90°旋转来增强数据集，其中DIV2K是Timofte[28]等发布的2K分辨率的高质量数据集，近几年被广泛运用在超分辨率领域，包含800张训练图片，100张验证图片和100张测试图片。为了验证算法的有效性，选取4个标准测试集：Set5[29]，Set14[30]，BSD100[31]，Urban100[32]进行测试。SET5、SET14和BSD100数据集中的图像由自然场景组成，URBAN100数据集包含具有挑战性的城市场景图像以及不同频段的细节。

训练时，碍于内存限制，DB块采用6块，同时利用双三次插值法以因子k(k=2,3,4)对原始HR图像进行下采样，生成相应的低分辨率图像，并将HR图像对应的小波图像作为训练标准，然后对每一次迭代后的结果利用式(7)进行损失计算，采用ADAM优化器进行更新权重和偏置，初始学习率设置为0.001，训练过程中当连续10个epochs损失函数没有降低时将学习率削减一半，当学习率低于0.000 02时停止整个训练过程。

对于原始彩色图像，将每张彩色图像从RGB颜色空间转换为YCbCr彩色空间。由于人眼视觉相比于颜色对图像亮度更加敏感，且在Y通道做映射关系不会影响图像的重建质量，所以仅对Y通道即亮度通道做训练从而得到对应的映射关系，对Cb、Cr 颜色分量进行简单的插值放大，这样可以在减轻计算开销的同时保证图像的重建质量。

3.3 实验结果及分析

基于文中算法流程，分别利用训练集和测试集进行了实验，同时对SRCNN[9]、VDSR[13]、LapSRN[16]、DWSR[22]等进行了复现。由于实验环境等差异，复现后的数据可能与原文献实验数据有些许差异。

评价超分辨率图像质量主要分为主观评价和客观评价，前者是通过观察者的主观感受来评价重构图像质量，后者是根据量化指标来衡量输出图像质量。其中，量化指标采用图像超分辨率常用的峰值信噪比(Peak Signal to Noise Ratio, PSNR)和图像的结构相似性(Structural Similarity, SSIM)。PSNR是基于MSE定义：

.

(8)

PSNR定义为：

(9)

式中，I和K表示两个m×n的图像，MAXI是图像可能的最大像素值，通常PSNR越大，失真度越小。SSIM定义：

(10)

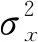
在客观评价上将本文算法同双三次线性插值(Bicubic)、SRCNN、VDSR、LapSRN、DWSR、Du[20]和SDSR 7种方法在4个测试集上的×2、×3、×4放大倍数进行对比，对比结果为6次实验的平均值，指标最高的数据加粗显示，如表1所示。从表1可以看出，相比传统Bicubic方法，基于学习的超分辨率重建方法在PSNR和SSIM上有着显著的优势。在基于深度CNN的方法中，本文算法指标全面优于SRCNN。相比于DWSR的10层简单网络，采用残差密集网络后，图像特征提取能力更强，同时获取浅层结构和细节信息更多，重建效果更优。相比于VDSR、LapSRN和SDSR，WRDSR在Set5、Set14和BSD100上测试结果基本持平，Set5和Set14上个别PSNR稍稍逊色于Du[20]。相比于其他算法，WRDSR在Urban100上优势明显，并且SSIM普遍高于其他算法，这得益于小波变换与残差密集网络相结合获取到了更多图像中不同层次的结构性信息，并且Urban100中以城市场景图像为主，富含不同频段的细节，结构性信息丰富，从而结构相似性更高，重建效果更加优秀。

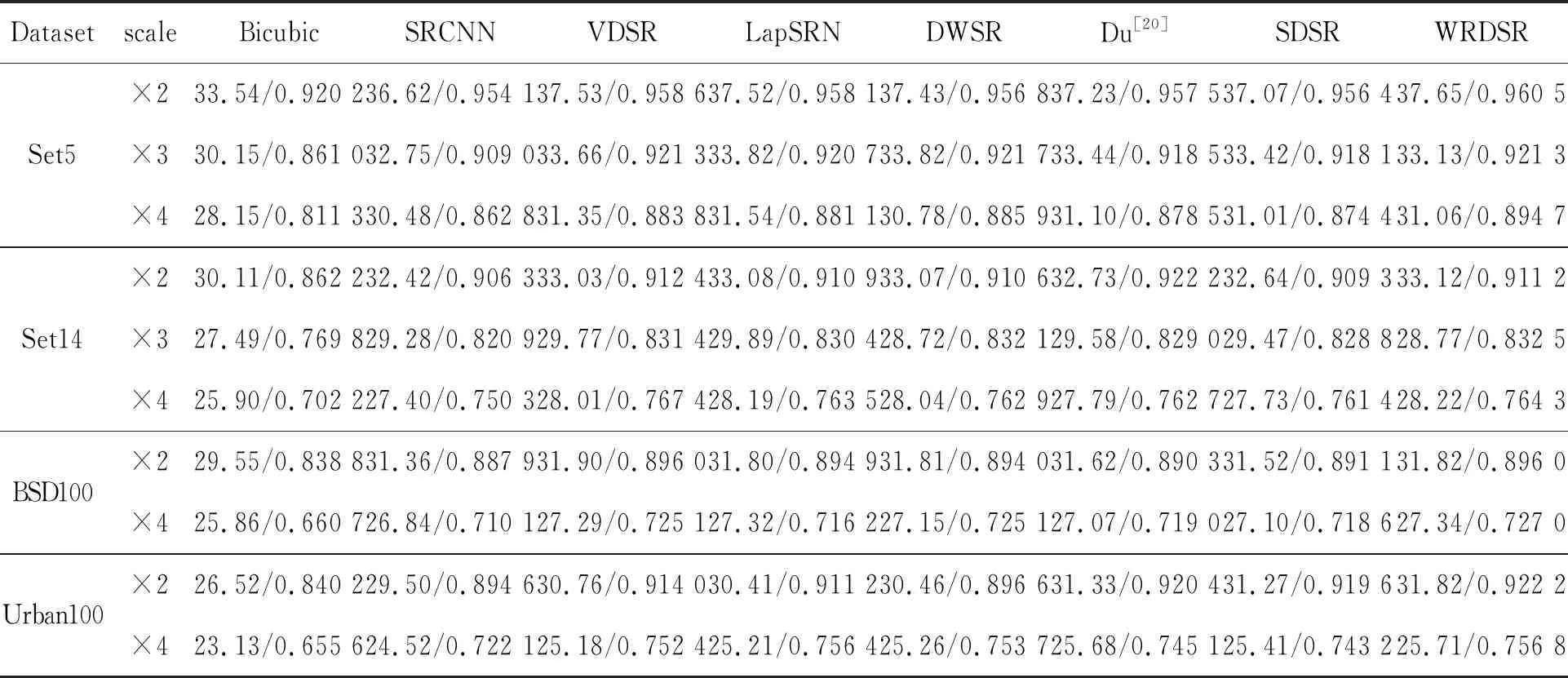
表1 PSNR/SSIM结果对比表

图5 标准测试集测试结果

在主观评价上，为了更加清晰地对比本文算法与其他算法的重建结果，分别从Set5的×2结果、Set14的×3结果、Urban100的×4结果中分别挑选一张图片进行比较，如图5所示。图5中，Set5蝴蝶图像测试结果很好地保留了黑色线条上的豁口以及纹理边缘的不平整性，而其他结果线条过于平滑，并未完整保留原始图像特征。Set14中No.1的重建结果在胡须等细节恢复优秀的基础上，整体直观感受更接近于原图。对于Urban100中No.92重建图像，本文方法生成的图像线条纹理更加清晰和锐利，线条沟壑的结构清晰可见，而其他结果中线条边缘比较模糊，信息损失严重。上述结果图中直观感受更强的原因是残差密集网络在提取图像特征时，有效地获取到更多由小波变换所提供的结构性信息，使得在重建图像时结构性更强，更加接近于原始图像。

本文算法在非标准测试集上也进行了测试以验证算法的普适性。测试集数据采集地点为东北林业大学帽儿山实验林场，以其30～40 年生的大叶榆、大果榆、裂叶榆、春榆等榆树上榆紫叶甲虫为研究对象，拍摄到200 张像素大小为500×375 的图片数据。测试图像进行3倍Bicubic下采样并通过WRDSR进行3倍放大得到测试结果，平均PSNR为35.29 dB，平均SSIM为0.938 9，测试结果如图6所示，其中第1行为原始图像，第2行为退化后图像经WRDSR恢复后图像。在对实际图像进行重建时，无论是榆紫叶甲虫还是树叶等背景图像，均得到很好地重建，树叶纹理清晰，孔洞等结构性信息很好地保留了下来。

图6 非标准测试集测试结果。(a)原始图像；(b)退化后经WRDSR恢复图像。

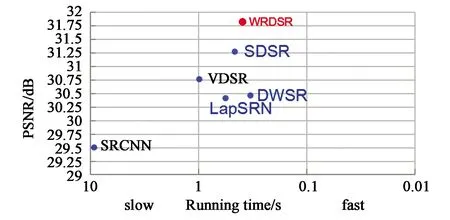
图7 WRDSR与其他5个算法在urban100数据集×2超分辨率重建的平均运行时间比较

(a) Learning rate： 0.01

(b) Learning rate: 0.001图8 收敛速度对比

基于深度CNN的6个SISR方法在urban100上×3超分辨率重建的平均运行时间对比上, WRDSR在保证了恢复质量的同时，算法的重建速度方面也具有一定的优势，参见图7。相较于DWSR的10层简单网络，WRDSR网络层数更多，结构更复杂，所以重建速度稍慢于DWSR。同时也可看出，WRDSR和DWSR两种基于小波变换的算法在重建速度上优于其他非小波域算法，这是缘于小波变换的稀疏性，使得网络参数大幅度减少，提高了网络的整体性能。

3.4 收敛速率

本文算法除主观评价与客观评价外，在收敛速率上较其他算法也存在优势。如图8所示，分别以0.01和0.001的学习率进行收敛速率实验，其中本文算法和DWSR在小波域下进行训练，Bicubic、SRCNN和VDSR在非小波域下进行训练。

通过两种学习率下的结果均可看出，小波域训练算法相较于非小波域训练算法收敛速度具有一定的优势，其具体原因如图9所示。大小为40×40的原始图像经小波变换后分成4个20×20的子图像，这样在训练时大大减少了卷积计算量，也缩小了重建所需的最小接收域。而相较于DWSR在小波域下，本文算法通过密集连接充分获取了各层次特征，在同等epoch下获取到了更多重建所需的信息，因而PSNR平均增长速度更快，收敛更早。

图9 小波变换样例

4 结 论

基于小波域的残差密集网络，可以很好地利用小波变换分离结构与细节信息的能力，同时也利用了残差密集网络对底层信息获取力强的优点，有效解决了传统图像超分辨率重建算法原始图像信息利用不足的问题。在客观评价上与算法Bicubic、SRCNN、VDSR、LapSRN、DWSR和SDSR相比，WRDSR在评价指标PSNR/SSIM上平均提高了2.824 dB/0.059 5、0.747 dB/0.016 8、0.016 dB/0.002 4、0.025 dB/0.004 3、0.21 dB/0.004 7和0.20 dB/0.005 7。主观评价上，重建图像具有更锐利的边缘和清晰的轮廓，更多地保留了原始图像的信息，具有更好的图像辨识度和视觉效果。