深水海底管道抛石防护结构石块粒径设计
2021-03-02孙青
孙 青
中海油田服务股份有限公司物探事业部,天津 300451
抛石技术在海底管道防护中应用广泛。抛石是指将一定直径的碎石沿管道路由堆积成石坝,用以保护管道以免管道受到拖锚和落物的冲击,可限制管道的屈曲位移,预防水流对结构物附近海床土壤的冲刷;而对于悬空管道,碎石还可以对管道下方空隙起到有效的填充和支撑作用。近年来,抛石技术向深水区域应用的趋势逐渐明显,南海多条海底管道采用抛石法进行防护,但随着水深的增加,由于深水抛石船舶的应用,造成作业成本的急剧增加,对石堆结构的防护效果也提出更高的要求。石块粒径对抛石防护结构的稳定性、耐久性以及海底管道的安全性起到至关重要的作用。针对在南海区域应用抛石防护结构对石块粒径选取的要求,国内学者获得以下研究成果:王裕霜[1]对海南联网工程后续抛石保护工程的石堆稳定性进行了设计论证和试验研究,给出了石料级配;王猛[2]以荔湾3-1管道的抛石保护为例,结合石块堆积的稳定性和管道抗冲击性能,计算了满足要求的石块粒径和石料分级方法;王怡[3]对采用局部抛石法治理管道悬空进行了水池试验,得到了不同水流流速下的石块稳定粒径;徐国[4]在琼州海峡海底电缆抛石防护工程中通过计算分析及试验研究确定了抛石块体的尺寸。在这些研究成果中,所做的水池试验针对性较强,但普适性较差,也存在计算公式形式单一、考虑因素不全面等问题。本文结合国内外抛石技术用于海底管道防护的研究和应用成果,对石块粒径的设计方法和计算公式进行梳理,为抛石防护结构设计中的粒径选择提供参考。
1 基于稳定性的粒径设计
抛石防护结构稳定性设计的目的在于确定石块在给定的石堆形状和波流条件下的最小稳定粒径。稳定性设计包括试验法和公式法两种,经过不断发展,石块稳定性计算的公式已有多种形式,可计算石块的静态稳定性和动态稳定性[5]。静态稳定性计算是基于单个石块起动的分析方法,该方法认为在设计环境条件下,不仅石堆的整体保持稳定,而且任意单个的石块也不会发生起动。而动态稳定性设计法则是一种允许石堆损失的设计方法,即允许石堆在极限风暴条件下存在一定的损失量。两种稳定性设计方法均可以给出石堆的中值粒径D50。
1.1 静态稳定性设计
根据CIRIA岩石手册[6]以及Thusyanthan[7]的研究,通常采用基于石块起动的临界剪应力理论进行静态稳定性分析,该方法计算的石堆稳定性由临界剪应力和外载荷作用在石块上的剪应力两者的比较结果决定。
Shields数ψ为环境载荷作用在石块上的剪应力的无量纲值,根据以下公式计算:

式中:τ为作用在石块上的剪应力,Pa;ρr为石块密度,kg/m3;D50为石块中值粒径,m;ρw为海水密度,kg/m3;g为重力加速度,m/s2。
CIRIA岩石手册推荐的临界Shields数Ψcr为:当Ψcr=0.03~0.035时,石块开始起动;当Ψcr=0.05~0.055时,石块有限制地运动。
1.1.1 海流作用下的剪应力
对于水深>40 m的海域,仅海流起决定性作用。海流作为定常流引起的剪应力τc(Pa) 计算公式为:

式中:U为剖面平均流速,m/s;C为Ch é zy系数,C=18 lg(1+12 h/ks);h为水深,m;ks为水动力粗糙度,m,对于石块可以取ks=4 D50。
1.1.2 波浪作用下的剪应力
对于水深≤5 m的海域,如近岸区,波浪起主导作用。在波浪引起的振荡流作用下,剪应力τw(Pa) 计算公式为:

式中:fw为摩擦因子;u0为海床表面处的波动轨迹峰值速度,m/s。
根据线性波理论:


式中:a0为海床表面处的波浪水平轨道运动幅值,m;T为波浪周期,s。
1.1.3 波流联合作用下的剪应力
在5~40 m水深范围内,需考虑波浪和海流联合作用下的剪应力,两者作用下的平均剪应力τm(Pa) 计算公式为:

波流联合作用最大剪应力τmax(Pa) 用于计算石块起动,计算公式为:
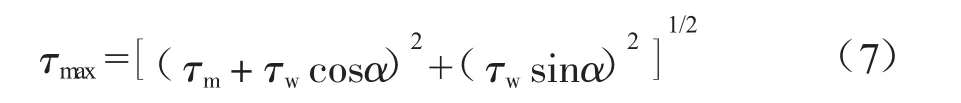
式中:α为波浪和海流之间的夹角,(°)。
1.1.4 位于斜坡上石块的临界剪应力
对于石堆来说,最易起动的是位于背流面斜坡上的石块,石块沿斜坡的重力分量会降低临界剪应力。对于有坡度的石块,其临界剪应力相比于水平面上石块的临界剪应力有一定折减,由下式计算:

式中:τβcr为石块位于坡角为β的斜坡上的临界剪应力,Pa;τcr为石块位于水平面上的临界剪应力,Pa;γ为水流相对坡度的遭遇角度,(°);φ为石堆的休止角,(°);β为坡度倾角,(°)。
1.2 动态稳定性设计
石堆的动态稳定性设计考虑了石块在波浪作用下的动态运动,石块个体的移动会导致石堆整体轮廓形状不断改变,直到最后形成一个新的石堆,进而需判断新石堆是否稳定。大部分用于计算石堆动态稳定性的公式采用石堆横截面损失面积的无量纲数S来表征。Van Gent和Wallast[8]对石堆在波流联合作用下的稳定性进行了模拟试验,根据试验结果,推导出了石堆损失量的计算公式,这也是CIRIA岩石手册推荐使用的计算公式。

式中:N为石堆整个设计寿命期内经历的波浪个数;θ为用来描述石堆移动性的无量纲参数;u0为波浪在石堆顶位置处产生的最大轨道速度,m/s;Δ为石块密度与海水密度的比值。
Tørumd等[9]的研究表明,用于覆盖海底油气管道的石堆,可允许的石堆损失量很小,允许损失量S可设为50。
2 基于安全性的粒径校核
根据管道及其附属设施能够承受的石块最大冲击力来确定石块的最大粒径D100。参考挪威船级社DNV-RP-F107规范[10]中对于管道受重物冲击的建议,对管道及其混凝土配重层等进行校核,将不规则形状的石块按照等效立方体和等效球体分别进行计算[6]。
单个石块在水中下落过程中受到石块自身重力W、浮力B以及下落过程中阻力的作用,根据牛顿第二定律,有如下关系:

式中:v为石块下落速度,m/s;t为下落时间,s;m为石块质量,kg;CD为石块在水中的阻力系数;A为石块截面积,m2。
通过求解微分方程可以计算得到石块下落速度随时间的变化情况,石块下落距离与下落时间关系可以根据公式计算得到:
根据石块下落初始位置到管道之间的距离,确定石块下落到碰到管道所经历的时间t,再根据下落时间t确定单个石块下落并触碰到管道时刻的冲击速度v。当大量石块同时下落时拖曳力系数会显著下降,使石块到达管道时的速度大幅提高,通常是单个石块下落速度的2~3倍。根据修正后的冲击速度计算对管道及混凝土配重层的冲击功Eimpact(J) 为:
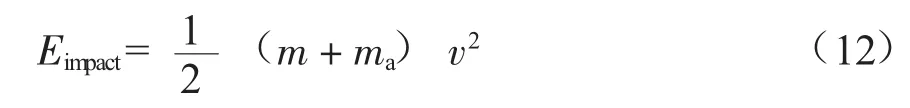
式中:ma为石块下落过程中的附加质量,kg。
根据DNV-RP-F107推荐公式,计算海底管道钢管最大允许吸收能量E(J):
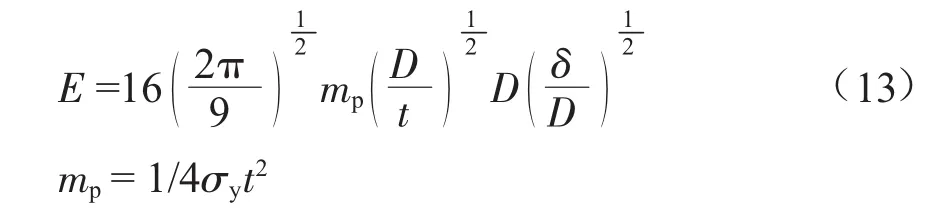
式中:mp为管壁极限塑性弯矩,N;t为钢管壁厚,m;D为钢管外径,m;δ为凹痕尺寸,m,最大允许凹痕尺寸的计算基于材料破坏等级D1(微小损伤),该损伤下不会造成烃泄漏并且无需修理;σy为管壁屈服应力,Pa。
根据DNV-RP-F107规范,混凝土配重层最大允许的吸收能量为:

式中:Y为混凝土层的压碎强度,Pa,通常为3~5倍的立方体强度;b为石块宽度,m;h为石块高度,m;x0为石块冲击混凝土层时的下陷深度,m,取混凝土层厚度的5%。
3 基于防渗功能的粒径设计
抛石防护结构的防渗设计是一种考虑防止海床沉积物受水流冲刷而从石堆孔隙中渗出的设计。在进行防渗设计时,既要保证海床沉积物不会渗出,又要保证石堆具有一定的渗透性,能够允许水流通过,以防止孔隙水压力过大。一般抛石防护结构设计成多层形式,内层为防渗层,外层为防护层。基于De Graauw[11]公式进行的石堆防渗层设计,要求水流引起的防渗层的水力坡降小于临界水力坡降icr,防渗层水平临界水力坡降计算公式:
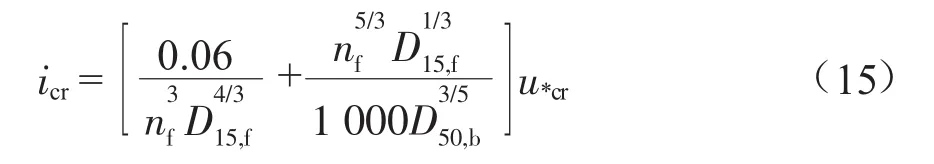
式中:icr为临界水力坡降,m,平行于防渗层与海床之间的接触面;D15,f为防渗层石块的15%筛上粒径,m;D50,b为海床沉积物的中值粒径,m;nf为防渗层石堆的孔隙率;u*cr为海床沉积物临界剪切速度,m/s,当海床沉积物为砂性土时,可以采用公式:
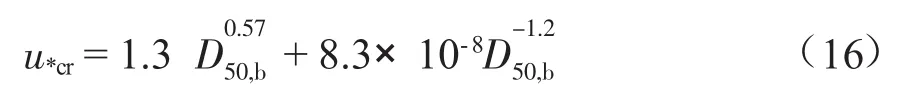
水流流经石堆引起的压力变化值ΔP根据以下公式计算:

式中:Cp为压力系数,定常水流下Cp=1,波浪下Cp=3。
根据以上公式,由海床沉积物粒径D50计算得到防渗层可用最大的D15粒径石块。为了防止防渗层石块从防护层渗出,防护层也要满足最小水力坡降要求。由防护层的石块D15粒径计算得到防渗层可用最小中值粒径D50。
4 管道抛石粒径设计案例
南海某管道钢管外径508 mm,壁厚14.3 mm,采用X65钢,混凝土配重层厚度为50 mm。为了预防和治理管道悬空而采取抛石方法,石堆设计横截面如图1所示,石堆共分两层,内层与管顶平齐,填充管道下方悬空部分,外层高出管顶0.5 m,起到增加稳定性和保护作用。石堆整体坡度比为1∶2.5,所选石块密度为2 600 kg/m3。
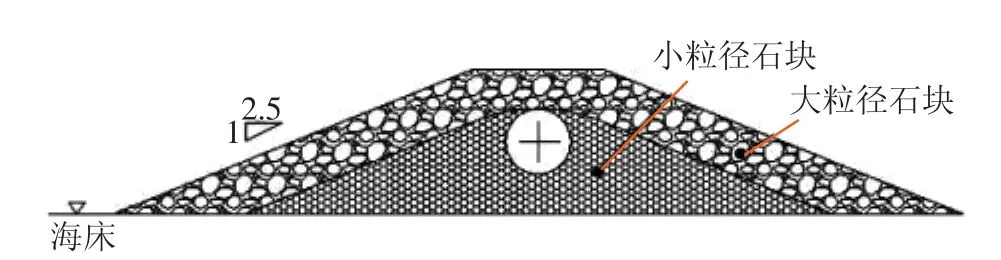
图1 石堆横截面
管道位于110 m水深的海域,所处位置的设计底部水流速度为2.2 m/s,由于水深较深,不考虑波浪载荷作用,所处海域抛锚风险低,不涉及拖锚防护问题。
4.1 外层石堆最小允许D50粒径
基于静态稳定性设计,对海流在石块上产生的剪切力与临界剪切力进行比较,得到当坡度比为1∶2.5时的最小允许D50粒径为70 mm。
4.2 内、外层可用最大粒径D100
根据DNV-RP-F107规范,对最大粒径200mm的石块从距海床5 m高度下落进行冲击校核,管道的最大允许吸收能量为6 071 J,混凝土层最大允许吸收能量为8 973 J。通过校核计算,其结果如表1所示,200 mm粒径石块下落的冲击能量在管道整体承受能力范围之内。

表1 石块下落冲击校核
4.3 内层允许最大D15粒径
管道路由海床沉积物为松散的砂性土,土壤中值粒径为0.13 mm。通过比较海流引起的水力坡降与临界水力坡降,计算当内层石块D15为200 mm时,石堆内层的临界水力坡降为0.025,海流流经管道附近引起的水力坡降为0.027。根据计算结果,内层石块D15小于200 mm可以满足防渗设计要求。
4.4 内层允许最小D50粒径
按照4.3节同样的方法,计算当外层石块D50为100 mm时,内层允许的最小中值粒径D50为0.2 mm。
5 结论
从海底管道抛石防护结构稳定性、安全性、防渗性等方面的考虑,根据公式计算出石堆设计石块的特征粒径,包括:外层石堆最小允许D50粒径,经校核通过的内、外层可用最大粒径D100,以及可以满足防渗要求内层允许最大D15粒径和最小D50粒径。
从结果可以看出:因波浪作用可忽略不计,深水抛石防护结构即使选择较小中值粒径石块(小于125 mm),仍能在海流作用下保持良好的稳定性。
对于表层为砂性土的海底,相比于需要考虑波浪的浅水来说,深水底部水流引起的水力坡降较小,即使不设置防渗层仍能满足防渗要求,因此对于有混凝土配重层管道的抛石防护,可以设计成单层石堆,这也将在一定程度上节约作业成本。
