基于弹性地基梁法的LNG储罐环向预应力方案设计

王志超，孙长军，张志红，沈 殷

1.柳州欧维姆机械股份有限公司，广西柳州 545006

2.同济大学，上海 200092

近年来国内外天然气市场需求旺盛，因此对于天然气的存储需求也逐渐增多，许多地区纷纷规划建设液化天然气接收站[1]。无论是LNG的液化站还是接收站，都需要格外关注其安全问题，通常做法是将LNG封存于一个密闭的安全容器中，以保证天然气不会泄漏或泄漏后事态可控。一般大型LNG储罐按照结构形式可分为单容罐、双容罐、薄膜罐及全容罐，由于全容罐可以承受内罐泄漏的LNG及其气体，不至于进一步扩散至外界，安全性较高，因此全容罐已成为目前LNG储罐的主流形式[2]。

本文以弹性地基梁理论为基础，对LNG全容罐的力学模型进行简要分析，给出了基于弹性地基梁的LNG储罐罐壁内力计算公式，可为储罐的环向预应力方案设计提供理论参考。

1 计算理论

1.1 LNG储罐外罐受力特性

典型的LNG储罐外罐结构形式如图1所示，由刚性底板、储罐罐壁及拱形穹顶三部分组成。罐壁与底板通常现浇为一个整体，穹顶与罐壁通常分别浇筑后连接在一起。穹顶结构承受自重、罐顶活荷载（风、雪、人等）以及内部气压荷载，在上述荷载的组合下，穹顶结构受力并不大，因此仅在穹顶内布置普通钢筋就可以满足混凝土抗裂要求。罐壁结构在正常工作时，承受罐顶传递的荷载、罐壁自重；在发生泄漏工况时，液体会对罐壁产生静水压力和泄漏的气体气压，同时也会受到温度荷载的作用。在上述荷载的组合作用下，罐壁的竖向和环向均会受到很大的拉力，这些力如果全部由混凝土承担则需要将混凝土构件的截面设计得非常大，因此通常配置预应力钢筋来平衡截面拉力，以减小罐壁厚度，提高结构经济性。储罐底板刚度较大，通常坐落在地基或桩基上，仅配置普通钢筋即可满足要求。

图1 LNG储罐结构示意

由于LNG储罐结构复杂，在进行结构设计时通常采用有限元法进行设计结果校验，有限元法模拟结果虽然相对准确，但建模和分析过程复杂，且需要定义预应力筋位置和数量[3]，试算所花费的时间成本相对较高，因此比较适合于后期施工图设计阶段。显然，在LNG储罐初期的方案设计阶段，希望得到一种快速简便的预应力布置方法。郑建华等[4]基于等效预应力荷载平衡的方法，提出了一种快速简便的储罐罐壁预应力计算方法，但是该方法没有考虑顶板、底板对储罐罐壁的约束作用，且需要根据工程师的主观经验多次调整才能最终确定预应力配筋方案。

根据LNG外罐的受力特征，在进行环向预应力设计时，可以将储罐进行适当简化。储罐底板简化为刚性体，罐壁与底板简化为刚性连接，罐壁与穹顶简化为弹性连接，并假定罐壁为薄壁型圆筒结构。进行内力计算时，罐壁设计液面以上受到泄漏气压PA（Pa）作用，设计液面以下受到LNG液体静水压力PL（Pa） 及泄漏气压PA（Pa） 作用，罐壁顶部受到穹顶结构的水平推力FH（N/m） 作用，穹顶对罐壁的约束可等效为弹性支撑，弹性系数为kd（N/m2），如图2所示。

图2 LNG储罐罐壁荷载分解模型简化示意

1.2 薄壁筒结构弹性地基梁模型

在轴对称荷载作用下的罐状容器如LNG储罐等，沿竖向取其一部分模型，可将其简化为弹性地基梁模型，其中“地基”与“梁”的概念都是抽象的[5]。圆柱形薄壁壳体受力简图见图3。

图3 圆柱形薄壁壳体受力分析

图3中储罐壁厚为t（m），半径为R（m），取单位弧长（1 m宽弧长）的罐壁进行分析，沿壁由上至下建立直角坐标系。则在轴向对称荷载P（x）（N/m2）的作用下罐壁产生径向位移y（m），则罐壁的环向应变εt为：

应力σt（Pa） 为：

式中：E为罐壁弹性模量，Pa。

轴向单位高度内的环向拉力T（x）（N/m）为：

因此，单位弧长罐壁环向张力形成的径向合力N（x）（N/m2） 为：

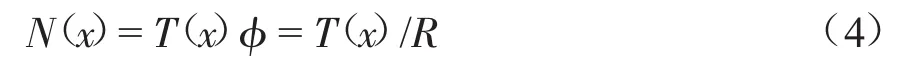
式中：φ=1/R，为单位弧长罐壁对应的弧度。

环向张力对筒壁径向变形形成地基反力N（N/m2），其地基反力弹性系数k（N/m3） 为：

由此建立的罐壁弹性地基梁位移微分方程为：

式中：I为单位宽度（弧长方向）罐壁截面惯性矩， m3。

罐壁在发生轴向弯曲时，径向变形会受到约束，这种约束可视为环向弯矩Mt（N·m/m），而环向弯矩与单位宽度内罐壁上的轴向弯矩M（N·m/m） 关系为：

式中：μ为材料泊松比。

由于罐壁与穹顶连接，罐顶径向位移也会带动穹顶变形，并在穹顶内产生环向张力T（dr）（N/m）。假定可以将拱形穹顶简化为三角形穹顶，见图4，则根据穹顶不同位置半径（rm） 与穹顶边缘R（m）的几何关系，就可以得到穹顶内不同位置的环向张力：

图4 拱形穹顶简化为三角形拱顶（剖面图）

式中：αqd（rad）为穹顶倾角，其值为穹顶矢高f（m）与罐壁半径R（m） 比值的反正切值，即αqd=arctan（f/R）。

进一步可得单位宽度范围内水平径向力N（dr）=cos（αqd）T（dr）φ=cos（αqd）T（dr）/r，N（dr）（N/m2）沿径向积分可得径向力合力N（dN/m）。

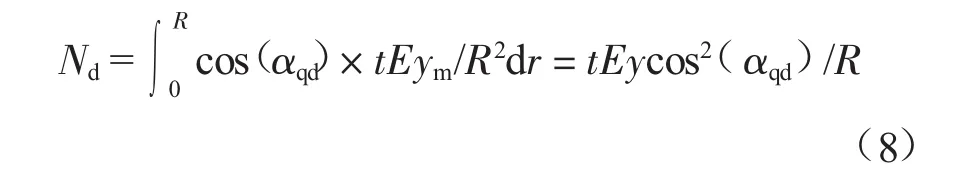
故可求得穹顶结构对罐顶水平位移产生的地基反力弹性系数kd（N/m2）：

引入4λ4=k（/EI），则可求得式（6）对应的齐次通解：

式中：Y0（m）、θ0（rad）、Q0（N/m） 及M0（N·m/m）分别为筒壁原点处的位移、转角、剪力和弯矩值，其中Y0、θ0为待定参数，M0=0，Q0=FH-kdY0（M0和Q0储罐弯矩和剪力的边界条件，其中将罐顶弹性支撑取消，代之以支反力）。由于式（6）右边的荷载并非连续函数，因此在求式（6）的非齐次通解项时，需要将等式右边的荷载项P（x）拆分成3个连续函数，再进行叠加求解。式（6）的非齐次通解解析式如下：

式中：PLH为液体在罐底产生的静水压力，即PLH=PL（H）=γ（H-HL）；γ为液体容重，N/m3，其分布范围由设计泄漏液面HL至罐底H。根据地基梁挠度与各参量之间的关系，可得：

对于壁底固结的结构，其边界条件为：

将式（13） 代入式（11）、式（12），可得到对应的未知参数Y0、θ0，得到方程特解。

2 计算实例

在上述推导过程中，进行了一定程度的简化，势必会造成理论计算结果与实际结果的差异，为此通过LNG储罐实例来分析理论计算公式的精确性，计算以通用有限元软件ABAQUS求解的结果为参考值。某LNG储罐模型参数见表1。在计算时，不考虑穹顶上部的设备自重及人员等附属荷载，以便对计算结果进行对比分析。

2.1 LNG储罐有限元模型

LNG储罐模型全部采用实体单元建模，结构采用弹性设计分析，故计算中混凝土材料采用线弹性材料。由于理论公式中未考虑钢筋的作用，为了便于对比，在进行有限元验证时，同样不考虑混凝土内配筋。

由于结构及边界条件的对称性，因此可以仅建立1/4模型进行计算，其有限元模型如图5所示。

图5 LNG储罐1/4有限元模型

2.2 计算结果对比

本文采用两种方案计算LNG储罐的径向位移及罐壁环向内力，第一种方法是采用弹性地基梁模型计算出罐壁径向位移，进一步计算出罐壁环向拉力T；第二种方法是采用有限元软件ABAQUS对储罐进行同工况分析，求出罐壁径向位移及罐壁应力，并采用池壁厚度的中心垂向路径应力换算出池 壁环向拉力T。采用有限元软件计算得到的径向位移云图如图6所示。

图6 LNG储罐径向位移云图/m

从图6可以看出：LNG储罐罐壁径向位移由下至上先增大后减小，超过LNG泄漏液面后逐渐趋于平缓，到罐顶之后会有小幅增大。罐壁最大径向位移位于距罐底12倍壁厚高度位置处。罐壁受力最大的底部径向位移反而不大，这是因为越靠近罐底的位置，罐壁受到罐底底板的约束作用越大，径向位移越小。

图7为弹性地基梁法理论结果与有限元结果的对比图，可以看出两种方法的径向位移结果基本一致，但在罐顶范围内有部分误差，罐顶附近的最大误差率约35%，除罐顶附近的位置外，其余部分二者的误差率均在5%以内。

图7 两种方法径向位移对比

图8为LNG储罐环向应力云图。

图8 LNG储罐环向应力云图/Pa

根据LNG储罐环向应力云图，沿罐壁中心设置一道路径，导出沿路径上的应力值，进一步换算出等效环向拉力，将其与理论公式计算的结果进行对比，如图9所示。

图9 两种方法环向拉力对比

LNG储罐的环向拉力与其径向位移成线性关系，同径向位移一样，采用弹性地基梁法理论公式得到的环向拉力与有限元结果基本一致，但在罐顶范围内有一定的误差。罐顶附近的最大误差率约30%左右，其余位置误差率均在5%以内。

造成罐顶计算误差的主要原因如下：

（1）在计算穹顶在罐顶形成的地基弹性系数时，将拱形穹顶简化为三角形穹顶，导致计算的地基弹性系数偏大。

（2）本文的计算理论中，假定穹顶罐壁铰接，忽略了少量的罐顶弯矩。

（3）本文的计算理论中，假定穹顶剪力作用于罐壁顶部，且未考虑环梁作用。

2.3 环向预应力钢筋的方案设计

根据前述罐壁内力计算结果，分段配置环向预应力筋，并在储罐顶部进行加强设计。配置原则如下：

（1）按照施工能力，拟定施工段高度，同高度范围内的预应力束配置应尽量相同。

（2）根据施工段内的环向拉力，绘制包络图，并留有一定余量使混凝土罐壁始终处于受压状态，如图10所示。

图10 LNG储罐罐壁环向预应力筋配置包络图

（3）储罐罐顶位置受力相对复杂，应进行设计加强。

本计算实例的预应力筋配置的设计包络，不同位置的预应力筋配置数量可以依据本设计包络进行设计，计算公式为：

式中：nx为施工段内单位高度配置的预应力束数量；Td为储罐罐壁单位高度范围内环向拉力设计值；σpAp为单束环向预应力筋在储罐内建立的有效预应力，可参考相关规范[6]进行计算。

3 结束语

从弹性地基梁法及有限元法内力计算结果的对比来看，两种方法的计算结果非常接近，表明了通过弹性地基梁法进行LNG储罐环向预应力设计的可行性。在本文的设计案例中没有考虑LNG储罐穹顶承受的设备、人员等附属荷载，在进行实际工程的方案设计时，可以将除穹顶自重荷载外的其他附属荷载产生的水平荷载叠加于罐顶。由于本文的理论公式是在简化模型的基础上推导的，其径向位移在储罐顶部的计算结果较小，因此参考本文公式进行储罐环向预应力方案设计时，需要注意将储罐顶部进行配筋加强。待环向预应力筋配置方案确定之后，可以进一步通过有限元法进行细化设计。