基于CFD收敛提前终止和变复杂度模型的两级气动优化方法

2021-03-02缪佶龚春林李春娜

西北工业大学学报 2021年1期

缪佶, 龚春林, 李春娜

(西北工业大学航天学院, 陕西西安 710072)

小型无人飞行器由于其具有尺寸小、使用灵活、任务执行能力强等多项优势,近些年来在各个领域都受到了广泛关注。为了使飞行器具有更宽的飞行包线,更广泛的应用范围,其翼型需要拥有更优良的气动性能。因此,对小型无人飞行器翼型进行气动优化设计具有重要的意义。

气动优化对于飞行器设计是一种有效的辅助方法。早期的气动优化设计采用工程估算或面元法等低精度模型,单次分析耗时非常短,可以直接进行优化。随着CFD理论和高性能计算机的发展,CFD数值模拟由于具有较高精度而越来越多地被应用于气动优化问题求解。然而,由于CFD计算耗时很长,难以应用于大设计空间的全局优化。

基于代理模型的优化方法,由于能够大大缩减CFD计算成本,逐渐成为气动优化研究的重要分支和关键技术[1]。代理模型的概念最早在20世纪80年代被提出,其作用之一是在分析和优化设计过程中替代那些比较复杂和费时的分析[2]。代理模型方法不仅可以提高优化设计效率,而且有利于滤除数值噪声和实现并行优化设计[3]。常用的代理模型方法主要包括:径向基神经网络模型[4]、多项式响应面[5]、Kriging模型等。然而直接构建代理模型也存在一定的局限性,当样本点少时难以保证模型精度,样本点多时计算耗时很长。对于外形复杂、设计变量较多的气动优化问题,为了确保代理模型的精度,往往需要大量的样本点,从而导致计算成本过大。为了解决这一问题,变复杂度建模方法(variable-fidelity modeling,VFM)被提出[6],其主要原理是:同时引入高精度分析模型和低精度分析模型,通过计算高、低精度分析模型在样本点处的差异构建出变复杂度模型来描述优化问题,从而在保证优化精度的同时有效降低计算成本[7]。

Chang等[8]提出使用乘法标度函数得到低精度与高精度模型的差异,并据此建立变复杂度模型。Alexandrov等[9]提出了一阶加法标度和一阶乘法标度函数,基于标度函数建立了变复杂度模型并分别用于三维机翼和二维翼型的优化问题。Gano等[10]分别通过进行Taylor一阶和二阶展开的方式建立标度函数。该方法虽然能够降低模型的构建成本,但该建模方法属于局部近似建模,并不适用于全局优化问题。Leifsson等[11]提出了一种基于VFM的快速优化方法,其中大量的低精度气动数据通过结合半工程方法快速计算得到,少量高精度气动数据通过CFD计算得到,从而实现对机翼气动外形的快速优化。Zhang等[12]将VFM和期望改进(expected improvement,EI)加点准则相结合,提出VF-EI方法,并结合分层Kriging代理模型,高效求解全局优化问题。Song等[13]提出了一种新的变复杂度优化策略,初始只构建基于低精度样本点的Kriging代理模型,高精度样本点则通过EI等加点策略添加到样本点集中,不断对低精度代理模型进行修正,构建变复杂度代理模型,该方法能够有效降低由初始高精度样本点带来的计算成本。Han等[14]通过构建多级变复杂度分层Kriging代理模型的方法对二维翼型和三维机翼进行优化,相比单精度代理模型和两级变复杂度代理模型方法,其进一步降低了计算成本。

当前的变复杂度模型通过少量计算成本大的高精度样本数据修正大量计算成本小的低精度样本数据。为了缩减计算成本,气动优化问题中的低精度样本可以由以下方式得到[15]:对复杂外形进行简化,CFD数值模拟过程中采用网格数量少的粗糙网格。Leifur等[15]通过半工程方法计算低精度样本的气动参数,诱导阻力通过涡格法求得,零升阻力和激波阻力由片条理论得到,计算一个低精度样本的气动数据大约需要15 s,其结果与高精度的偏差在33%～50%。Alexandrov等[9]通过构建粗糙CFD网格的方式得到低精度样本响应值,计算成本仅为高精度样本的四分之一。Jiang等[7]将变复杂度模型应用于小水线面双体船的设计中,低精度样本响应值也通过粗糙CFD网格计算得到,其网格量为高精度样本的五分之一。Mifsud等[16]为得到低精度样本数据,不仅构建了粗糙CFD网格,且仅采用了一阶精度进行迭代计算,从而进一步降低了低精度模型的计算耗时,高精度样本数据则采用细网格和三阶精度迭代计算得到。

针对小型无人飞行器的翼型气动优化问题,为了使计算成本维持在较低水平,并保证优化结果精度足够,本文提出一种基于CFD收敛提前终止和变复杂度模型的两级气动优化方法:首先,通过CFD收敛提前终止的方法获得低精度样本响应值,通过CFD完全收敛获得高精度样本响应值,并利用加法桥接函数构建变复杂度模型。为得到精确的最优解,先后利用多岛遗传算法和Hooke-Jeeves算法分别基于变复杂度模型和高精度CFD分析进行全局-局部两级优化。最后,采用该优化方法对小型无人飞行器的翼型优化问题进行求解,表明了该优化方法的可行性和有效性。

1 优化方法原理

1.1 Kriging代理模型

Kriging模型最早由南非地质学家 Krige提出,并成功应用于地质勘查中。至今,Kriging模型已成为优化设计领域最具代表性、应用最广泛的代理模型构建方法之一[17]。Kriging模型是一种预测方差最小的无偏估计模型,具有较好的拟合能力,适用于强非线性问题的拟合[18]。

(1)

式中:f(x)=[f1(x),f2(x),…,fj(x)],j=1,2,…,k为回归函数;β={β1,…,βj}T为回归系数;z(x)为满足N(0,σ2)正态分布的随机变量,方程右侧两项分别代表预测值的总体趋势和局部偏差。定义n×k的矩阵

F=[fT(x(1)),fT(x(2)),…,fT(x(n))]T

(2)

在整个设计空间内,不同样本点之间的关联程度通过相关函数来描述。常用相关函数有高斯函数、指数函数、线性函数、球函数、三次函数和样条函数等[19]。本文选用高斯函数作为相关函数,则样本点的协方矩阵表示为

Cov[z(xi),z(xj)]=σ2R[z(xj),z(xj)]

(3)

1.2 变复杂度模型

单独基于CFD数据建模会导致建模代价过大,而单独基于低精度数据建模会难以保证模型精度。为了兼顾计算代价大的高精度模型和精度低的低精度模型,建立变复杂度模型是一种十分有效的方法。变复杂度方法可通过少量高、低精度样本的差异构建差异响应模型,从而修正其他低精度响应值以建立代理模型或直接针对修正后的响应值进行优化,变复杂度模型通常可以表示为

(10)

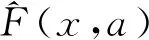
首先,对低精度模型和高精度模型选取m个相同的采样点并计算相应的高、低精度响应值,然后计算m个采样点处高低响应值间的差异,并建立差异响应模型。最后将差异响应模型作为低精度与高精度响应的桥接,修正低精度响应值,从而建立变复杂度模型。修正方法可采用乘法标度或加法标度,表示如下

在加法修正和乘法修正中,C(x,a)是差异响应模型,预测高、低精度模型的差异。在实际应用中,加法标度函数在气动优化问题中适用性更广,而乘法标度函数可能出现奇异点,故本文采用加法标度函数构建变复杂度模型。由于低精度样本的计算成本很低,不需要选取大量低精度样本构建代理模型,可以直接基于修正后的响应值进行优化。

2 基于CFD收敛提前终止和变复杂度模型的两级优化方法

2.1 CFD提前终止收敛

构建变复杂度模型所基于的低精度样本与高精度样本数据存在一定误差。文献[15]通过半工程方法得到低精度样本零升阻力、诱导阻力以及激波阻力,与高精度样本结果的相对误差范围为33%～50%,这种过大的差异会导致需要更多的高精度样本,使得计算成本增加。根据经验,高、低精度数据的相对差异在20%以内往往可以获得精度较高的变复杂度模型,且低精度样本的计算耗时应维持在较低水平,以确保优化成本较低。

文献[8]通过使用粗糙CFD网格的方法获得低精度数据,使得低精度模型构建成本仅为高精度模型的1/8。然而,粗糙网格受几何模型的影响较大,外形越复杂的模型所需要的网格数越多。若对外形复杂的模型生成粗糙网格,由于优化过程中几何外形在不断地改变,有可能因网格量少或网格尺寸大,导致网格质量过差,从而使得CFD结果精度过低或网格生成过程失败。因此,采用粗糙网格的方法存在不稳定因素,会影响外形复杂模型优化的可靠性。为了在保证结果精度足够的同时尽可能缩减计算成本,本文采用CFD收敛提前终止的方法获得低精度数据。

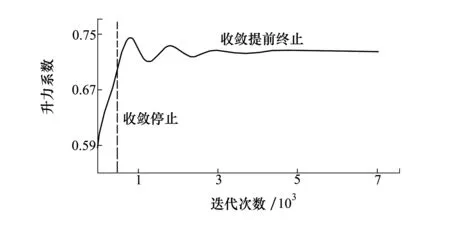
图1 CFD收敛提前终止示意图

CFD的收敛过程往往初始收敛很快,之后随着迭代步数的增加其收敛速度逐渐减缓。由图1所示,气动力系数仅需很少的迭代步数即可接近完全收敛的解,若提前终止收敛,则计算成本远远小于完全收敛,且结果相差不大。而且,对于高、低精度样本如果采用一样的细网格,网格质量能得到保证,使得气动优化过程具有很好的鲁棒性。

由于残差反映了当前流场与收敛的流场之间的差距,可以采用残差来作为流场提前终止收敛的判定准则。对于网格质量高的细网格模型,残差往往需要收敛到1×10-6才能使升阻力系数完全平稳,但残差越小气动力系数变化越小且收敛越缓慢,因此不等残差完全收敛即提前终止的话可以大大减少计算耗时。

本文采用RAE2822翼型作为小型无人飞行器的基准翼型。为了获得收敛提前终止准则,分别对残差收敛到1×10-2,1×10-3和1×10-4时的计算耗时和计算精度进行对比。采用RAE2822翼型的标准算例来对比不同残差收敛标准,该翼型的计算状态为:Ma=0.729,Re=6.5×106,α=2.31°。

首先通过网格收敛性验证,生成RAE2822翼型的细网格A1。网格收敛性验证结果如表1所示:

表1 网格收敛性验证

收敛性验证后确定的细网格A1的网格单元数量为82 643,壁面附面层满足Y+≈1,细网格A1的情况如图2所示。

基于该网格,对不同收敛准则下的计算耗时和计算精度进行对比,情况如表2所示。

综合考虑计算耗时和计算精度,选择1×10-3作为提前收敛的残差,此时计算耗时很少,仅为80 s,且与完全收敛结果的相对误差不大,均在20%以内,能够满足变复杂度模型所需的低精度数据要求。因此,本文将残差作为CFD收敛提前终止的条件:当残差达到1×10-3时即终止收敛。

图2 细网格

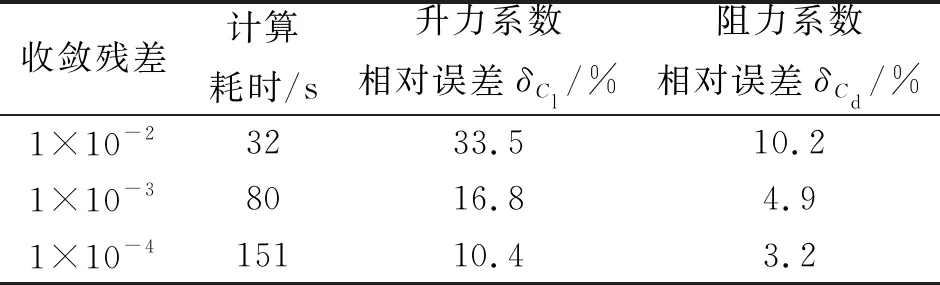
表2 不同收敛准则对比情况

为了确保细网格A1的计算结果准确,将其与相同计算状态的实验结果进行对比,对比情况如表3所示。为了将收敛提前终止方法与粗糙网格方法进行对比,除细网格A1外,再生成3个粗糙程度不一的网格M1,M2,M3,维持壁面Y+和边界层网格层数不变,适当降低壁面网格密度,M1,M2和M3的网格单元量分别为54 841,26 409和13 195。分别将这4个不同精度的网格用于CFD分析,并与CFD收敛提前终止方法得到的结果进行对比,结果如表3所示。

表3 采用不同粗糙度网格的CFD结果对比

可以看出,细网格A1得到的结果与实验结果十分接近,升阻力的相对误差可由(13)至(14)式计算得到

(13)

(14)

升力系数误差δCl约为1.2%,阻力系数误差δCd仅为0.8%,故可将A1网格视为基准网格。M1网格的计算结果与基准网格差别不大,与实验结果也比较接近。其运行时间相比基准网格减小了接近一半,但计算一个样本点仍然需要430 s的时间。M2的网格数为M1的一半,由于网格数的减小,网格质量有少量下降,依然需要运行360 s才能使结果收敛,M2得到的气动力系数仍较为接近真实结果。M3的网格数进一步减小了一半,但此时得到的结果已远远偏离了真实结果,且由于网格数量少,网格质量下降较多,仍需要300 s才能基本收敛,在优化过程的其他状态下存在发散的可能。

然而,细网格A1收敛提前终止得到的结果精确度虽然不如M1和M2网格,但与真实结果误差在20%以内,其升力系数Cl的误差为16.8%,阻力系数Cd的误差为4.9%,可以满足构建变复杂度模型的低精度样本需求。此外,其计算时间仅80 s,远远低于各粗糙网格的计算成本,更有利于全局优化问题的效率提高。

上述算例表明,随着网格量的减小,CFD的结果误差会逐渐加大。当网格数量减小到一定量时,相对误差会急剧增大,由5%增至45%。因此,当网格粗糙到一定程度时,其结果与精确结果的误差会骤增,从而无法作为低精度样本参与优化过程。为了生成合适的粗糙网格,需要做不同粗糙度网格的验证,否则随着气动外形优化的进行,模型的几何外形一直在变化,生成的粗糙网格非常容易在优化过程中引起迭代发散或精度过低。相比而言,CFD收敛提前终止方法的计算成本低于粗糙网格,相对误差同样可以满足低精度样本的要求;更重要的是,CFD收敛提前终止的方法不需要生成低精度网格,低精度样本和高精度样本都采用同一套细网格,在降低工作量的同时提高了优化过程的鲁棒性。

2.2 优化方法框架

本文提出的基于CFD收敛提前终止和变复杂度模型的两级气动优化方法的流程如图3所示,具体介绍如下:

图3 优化框架流程图

第一步对优化问题建模,包括目标函数,设计变量和约束条件。

第二步通过拉丁超立方试验设计方法[21]生成少量用于构建差异响应代理模型的样本点。

第三步在样本点处进行CFD模拟,获得相应的高、低精度响应值。

第四步在这些样本点处计算高、低精度响应值的差异,利用Kriging建模方法,构造差异响应代理模型

C(xi)=F(xi)-fl(xi)

(15)

F(xi)为样本点xi处高精度响应值,fl(xi)为相同样本点处的低精度响应值。

第五步将差异响应代理模型叠加在低精度样本点上,即可建立变复杂度模型,从而获得样本点处变复杂度模型的响应值。随机选取测试点,对比测试点处的高精度响应值与变复杂度响应值的差异,以验证变复杂度模型精度是否满足要求。若其精度足够,则继续第六步;若其精度不满足要求,则在代理模型误差最大处添加样本点,并返回第三步。

第六步基于建立的变复杂度模型进行第一级优化。采用多岛遗传算法直接基于变复杂度模型进行全局优化,获得最优解。

第七步以第一级全局优化得到的最优解为初值,进行第二级局部优化。采用Hooke-Jeeves算法直接基于高精度CFD分析进行局部优化,从而获得更精确的最优解。

3 小型无人飞行器翼型优化

3.1 优化问题建模

类别形状函数变换方法(class and shape transformation,CST)[22]是一种有效的几何外形参数表达方法,可以用较少的设计变量描述复杂外形[23],常应用于飞行器翼型和外形的设计。CST方法通过类型函数和形状函数来构建二维或三维的外形。根据文献,5阶伯恩斯坦多项式即可将原翼型拟合得十分精确,故本文采用5阶伯恩斯坦多项式描述RAE2822翼型的几何外形。因此,气动优化问题的设计变量一共12个,分别为描述上下翼面几何外形的12个伯恩斯坦多项式系数增量。

由于高亚声速状态下飞行器周围的流场变化更为复杂,对飞行器的飞行性能要求更高,故应重点考虑高亚声速下的翼型气动特性。参考多型高亚声速无人飞行器的飞行状态,本优化问题的设计状态确定如下:Ma=0.75,H=7 500 m,α=1°。优化问题的数学模型可表示为:

(16)

式中:s(x),Cl(x)分别为翼型面积和升力系数;S0(x)为优化前的翼型面积,其值为0.078,Cl0(t)为优化前的升力系数,其值为0.51。对于该翼型优化问题,由于飞行状态为跨声速,翼型表面会存在局部激波,故在该飞行工况下优化方向以降低激波阻力为主。而翼型面积大小主要影响摩擦阻力,故该优化问题将翼型面积作为约束条件,以体现该优化方法对减小激波阻力起到的效果。优化后的翼型面积不应小于初始翼型面积,优化后的升力系数不应小于初始升力系数。伯恩斯坦多项式系数增量变化范围应在-0.02和0.02之间。

小型无人飞行器初始翼型的气动网格采用前面分析过的细网格A1。CFD数值求解过程中采用有限体积法求解N-S方程,湍流模型为SSTk-ω两方程模型,空间离散采用二阶迎风格式,远场边界条件为压力远场,物面边界条件为无滑移壁面。

在构建初始VFM时,采用拉丁超立方取样方法生成35个样本点。为了证明低精度样本数据的有效性,对35个样本的高、低精度响应分布进行了对比,如图4所示。可以发现,低精度响应值与高精度响应值的相对误差不大,且变化趋势基本相同,升力系数Cl的平均误差约为13.69%,阻力系数Cd的平均误差约为5.04%,说明残差收敛到1×10-3时,低精度样本与高精度样本的相对误差保持在20%以内。此时的误差可以满足低精度数据的要求,即高、低精度样本可用于构建差异响应代理模型。

图4 高、低精度响应值对比

为验证变复杂度模型的精度,随机选取15个试验点,分别在试验点处进行CFD模拟得到高、低精度响应分布,通过差异响应代理模型修正低精度响应值,并将修正后的响应值与高精度响应值进行对比,结果如图5所示。对比图4和图5,变复杂度模型的精度相比低精度模型有了明显提升,修正后的响应值接近于高精度响应值。修正后的升力系数Cl与高精度结果平均误差为1.63%,修正后的阻力系数Cd与高精度结果平均误差为2.49%。因此,所建立的变复杂度模型可以代替高精度模型,并用于气动优化问题的求解。

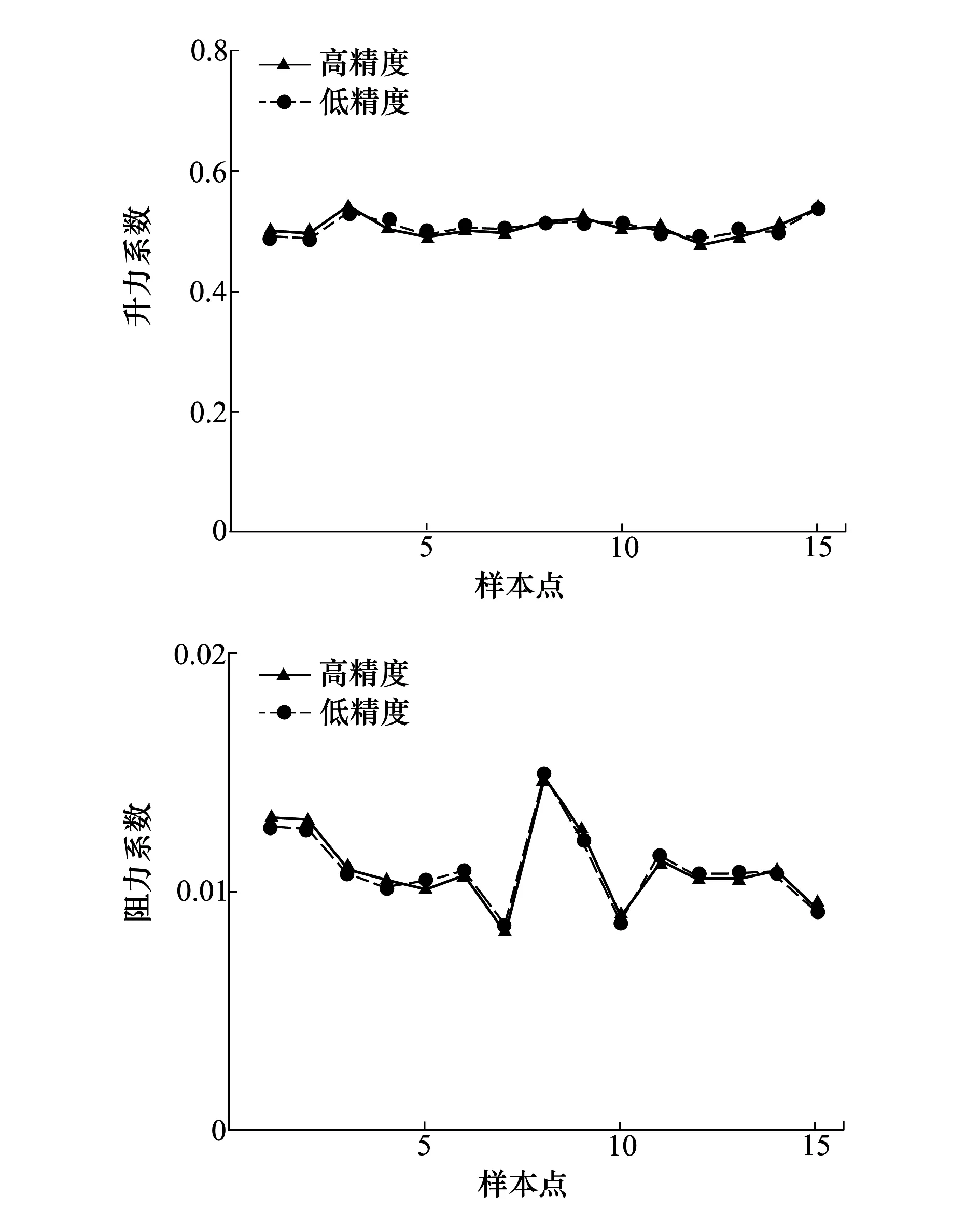
图5 变复杂度模型精度验证

3.2 优化结果

首先,直接基于变复杂度模型进行第一级优化,优化算法采用多岛遗传算法。相比于传统遗传算法,多岛遗传算法具有更好的全局求解能力和更高的计算效率。根据设计变量的个数和优化问题复杂度,多岛遗传算法的控制参数设置如下:岛数为5,子种群规模np=20,进化代数g=20,交叉概率pc=0.8,变异概率pm=0.01,岛间迁移率pt=0.1。

第一级全局优化收敛历程如图6所示,其中图6a)为目标函数阻力系数Cd的收敛历程,图6b)～6c)分别为2个约束条件升力系数Cl和翼型面积S的收敛历程。图6表明,目标函数Cd在收敛过程中有了明显降低,约束条件随着迭代进行在约束边界附近波动,故第一级全局优化效果比较明显。

用高精度CFD模型计算最优外形的气动性能,并计算相应的目标函数值和约束函数值。表4对全局优化得到的最优解与CFD计算的结果进行了对比。

图6 第一级全局优化迭代历程

由表4可以看出,变复杂度模型精度较好,优化结果与真实结果相差很小。其中,优化得到的阻力系数Cd与CFD计算结果相对误差为1.82%,升力系数Cl与CFD计算结果的相对误差仅为1.46%。上述表明,第一级基于变复杂度模型的最优解与高精度结果相对误差在2%以内,变复杂度模型具备较好的精度。

对比RAE2822翼型,阻力系数Cd经第一级全局优化有了显著改善,降低了约13.3 counts;由约束条件分析,升力系数Cl变化较小,依然满足约束条件,翼型面积S也与基准翼型相同,均为0.078,满足约束条件。

表4 基于变复杂度模型优化结果与该点对应的CFD分析结果对比

为了提高最优解的质量,以第一级优化得到的最优解为初值,采用Hooke-Jeeves算法直接基于高精度模型进行局部搜索。Hooke-Jeeves算法的原理是从基点出发,通过轴向移动依次沿着不同坐标轴搜索函数值更小的点,作为新的基点,之后沿着相邻两个基点的连线方向继续进行模式搜索,试图使函数值更快地减小。该方法程序简单,无需计算梯度,适应性较强,且局部搜索收敛快、效果好,适用于该优化问题。第二级局部优化迭代历程如图7所示,根据该算法的原理,选择目标函数在连续25个迭代步均无法进一步改善作为优化终止判断标准。当目标函数无法进一步改善时,即认为优化已达到局部最优,故可取优化过程中的目标函数最优值作为该优化问题的局部最优解。

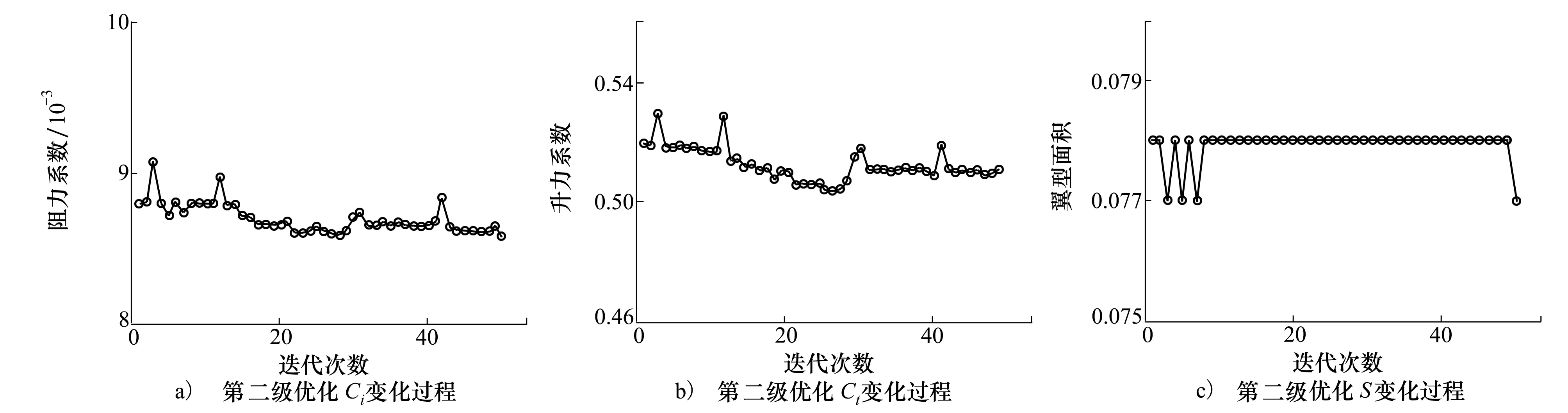
图7 第二级局部优化迭代历程

图8 优化前后翼型对比

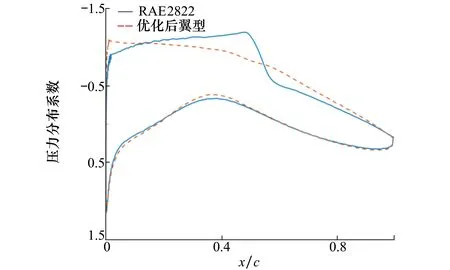
图9 优化前后压力分布对比

第二级局部优化共调用50次高精度模型,计算耗时约为10 h。可以看出,相比第一轮优化的结果,目标函数Cd在第一轮优化的基础上继续降低了2 counts,这说明第二轮优化可以进一步提升优化结果的精度,体现了两级气动优化的有效性。约束条件Cl相比第一轮优化结果也仅有微小变化,仍然满足约束要求。小型无人飞行器的初始RAE2822翼型与优化后翼型的气动性能对比情况如表5所示。

表5 初始翼型与最优翼型气动性能对比

小型无人飞行器的初始翼型与优化后翼型的外形和压力分布对比如图8和9所示。由图8外形对比可以看出,翼型中前段弯度变小使压力峰值前移,压力恢复变缓,激波变弱。由图9压强分布对比可以看出,翼型下表面的压强分布在优化前后变化不大,主要差异在于翼型上表面。初始翼型在上表面前部压强缓慢减小,在中部达到峰值后压强激增,从而产生强激波,而优化后由于压强峰值前移,整个上表面压强始终在缓慢增加,因此避免了压强的激增,激波大大减弱。

图10a)至10b)分别为小型无人飞行器的初始翼型和优化后翼型的流场压强云图。可以看出,初始RAE2822翼型在上表面中部存在非常明显的强激波,而优化后消除了强激波,显著地减小了激波阻力。

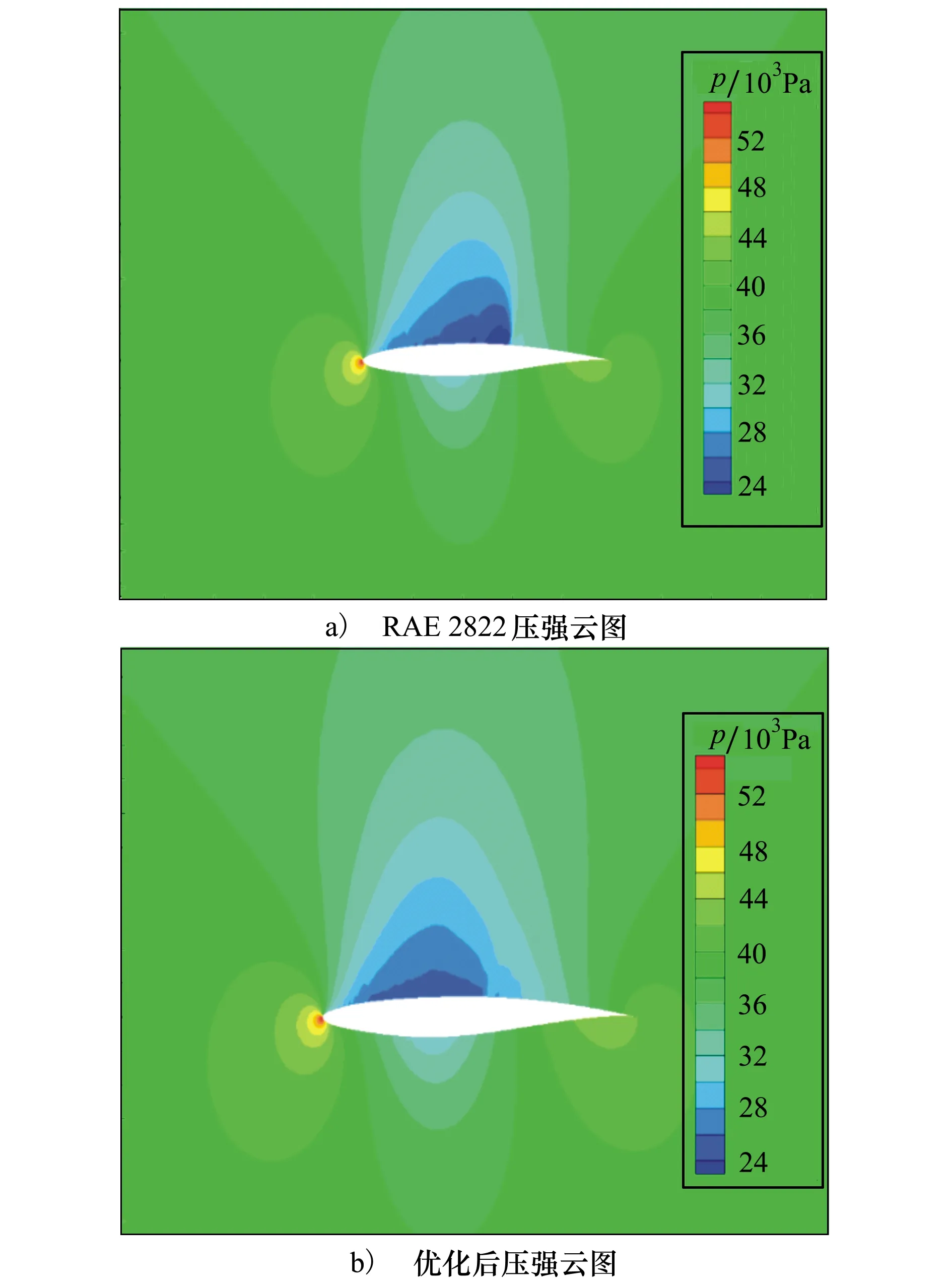
图10 优化前后压强云图对比

采用本文基于CFD收敛提前终止和变复杂度模型的两级气动优化方法对飞行器翼型进行优化设计后,目标函数Cd总共降低了15.1 counts,且Cl和S均满足约束条件,因此提出的气动优化方法效果良好,可以获得理想的最优解。

3.3 与基于单一精度代理模型的优化结果对比

为了评估本文提出的两级气动优化方法的性能,采用基于单一精度Kriging代理模型的EGO方法对该翼型优化问题进行了求解,并将优化结果与3.2节中结果进行了对比。其中,CFD计算从网格到流场求解器均与3.1节中设置相同。文献[24]指出,为了使初始代理模型精度足够,通过试验设计获得的初始样本点数应该大于m(m+1)/2,m为设计变量个数,故将构建VFM用到的34个样本点和额外生成的44个样本点共同作为初始样本点,用CFD完全收敛的高精度模型求解相应的响应值来构建初始Kriging代理模型。此后,采用EGO方法对该翼型优化问题进行求解。最终,采用EGO方法获得的最优Cd为0.008 56,相比基准状态降低了15.7 counts,而本文提出方法获得的最优Cd为0.008 62,2种方法的优化结果差异不到0.7%,故2种方法获得的最优解很接近。EGO方法的整个优化过程耗时约为84 h,而本文提出方法的总耗时约为50 h,故本文方法的优化耗时更低。优化结果对比如表6所示。