整体叶盘侧铣加工颤振可靠性预测

张楠, 史耀耀, 陈振, 陈红霞, 刘佳, 赵盼

(1.西北工业大学 航空发动机高性能制造工业和信息化部重点实验室, 陕西 西安 710072;2.内蒙古工业大学 机械工程学院, 内蒙古 呼和浩特 010062;3.内蒙古工业大学 航空学院, 内蒙古 呼和浩特 010062)

整体叶盘是新一代航空发动机实现结构创新与性能跨越的核心零部件[1-2]。整体叶盘将叶片与轮盘集成一体,省去了中间榫接结构,具有减轻质量、简化结构、减小气流损失、提高推重比、改善安全性和可靠性等优点。整体叶盘的叶片型面复杂弯扭大,叶盘通道窄而深,且毛坯材料通常为钛合金、高温合金等难加工材料。使其加工难度极大,被誉为制造业皇冠上的明珠[3-4]。

多轴数控铣削广泛应用于整体叶盘加工,侧铣常用于整体叶盘型面精加工[5]。由于整体叶盘通道较深,刀具的悬长较大,径向刚度较小,加工过程中容易发生颤振。颤振导致工件表面质量下降、刀具磨损加剧、生产效率受限[6-10]。因此,抑制颤振对加工过程至关重要。使用稳定性叶瓣图是避免颤振最有效的方法。稳定性叶瓣图为提高加工效率和参数优化提供了理论依据[11-17]。

传统的稳定性叶瓣图不考虑随机变量对切削稳定性的影响[18-21],Duncan等[22]首次研究了随机变量对稳定性叶瓣图的影响;根据标准偏差,利用结构参数的平均值、上界和下界确定3条稳定性叶瓣图的曲线;但没有给出表示不确定度影响的量化指标。为了解决此问题,Liu等[23]研究了随机变量对车削系统颤振稳定性预测的影响,并首次提出了可靠性叶瓣图。可靠性叶瓣图可用于确定颤振和无颤振区域,代替了传统的稳定性叶瓣图。颤振可靠性定义为加工系统的稳定性概率,可用可靠性叶瓣图来确定。

本文应用可靠性叶瓣图来判断侧铣加工系统的稳定性概率。将结构参数和主轴转速视为随机变量,以单自由度和二自由度铣削的轴向极限切削深度构造临界稳定状态下的性能函数;采用一次二阶矩法求解铣削加工系统的可靠性模型,确定系统的稳定性概率。

1 侧铣颤振的动态模型

1.1 侧铣加工动态模型

侧铣加工系统有2个自由度,如图1所示。假设侧铣刀有Nt个刀齿,则动态切屑厚度可以表示为[24]

hj(t)=[Δx(t)sinφj(t)+Δy(t)cosφj(t)]g(φj(t))

(1)

式中：

(2)

Δx(t)=x(t)-x(t-T)；Δy(t)=y(t)-y(t-T)；T是两齿之间的切削间隔时间;φst和φex分别是刀具的切入角与切出角。

图1 侧铣加工过程的动态模型

X,Y向的切削力可以表示为[24]

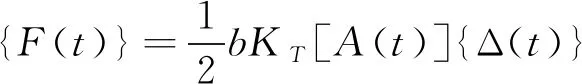
(3)

式中：

(4)

(5)

式中,KT,KR分别为切向和径向切削力系数,b为轴向切深。

当刀具旋转时,方向系数随着时间而变化。[A(t)]是以刀齿切削频率(ω(t)=2πnNt/60)为周期的,因此可以展开为傅里叶级数。利用傅里叶级数的平均分量,[A(t)]可以近似表示为[A0][24]

(6)

其中积分函数可以表示为[24]

(7)

动态铣削公式(3)可以简化为[24]

(8)

1.2 颤振稳定性叶瓣图

刀具-工件接触区域的传递函数矩阵可以表示为[24]

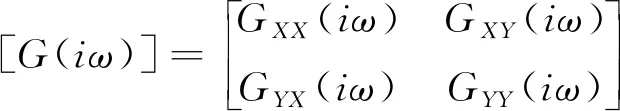
(9)

对于单自由度铣削系统,无颤振时极限轴向切深可以表示为[24]

(10)

式中:ωc为给定颤振频率,mX、kX、cX分别为X向的模态质量、模态刚度和模态阻尼。

对于二自由度铣削系统,无颤振极限轴向切深可以表示为[24]

dlim=

(11)

式中:

(12)

(13)

2 铣削颤振可靠性模型

将铣削加工系统的极限状态作为临界稳定状态。“失效”表示不稳定的加工状态,刀具的振动随着切削力无限地增加。“可靠”表示稳定的加工状态,刀具的振动会在阻尼作用下减弱。

铣削过程中刀具和工件的相互作用产生颤振。颤振频率与结构参数有关。铣刀的结构参数m,c,k和主轴转速S是铣削系统基本的随机变量。

考虑颤振的铣削系统极限状态函数可以表示为[25-26]

fX(X)=dlim-d

(14)

动态铣削过程的可靠性是在给定的时间和参数下不发生颤振的概率,该可靠性可以定义为[25]

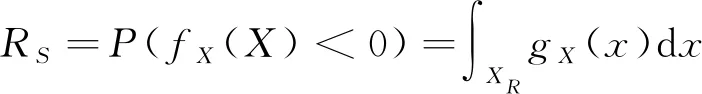
(15)

式中:X为随机变量向量,X=(m,c,k,ωc);结构参数m,c,k是独立的变量且服从正态分布;颤振频率ωc与m,c,k相关,它的分布规律与随机变量m,c,k和S有关。

3 一次二阶矩法

一次二阶矩法将失效面泰勒展开点的性能函数线性化。下面将介绍基于一次二阶矩法的铣削系统可靠性评估方法。

铣削系统的极限状态函数为[25]

Z=fX(X)=0

(16)

对于一个二自由度铣削系统,基本的随机变量X=(x1,x2…xi)T是不相关的,且服从正态分布,其中xi分别为mX,mY,cX,cY,kX,kY和ωc。颤振频率ωc与mX,mY,cX,cY,kX,kY相关。铣削系统的相关矩阵可以表示为

(17)

式中:ρxixj是变量xi和xj的相关系数。

标准偏差ζmX,ζmY,ζcX,ζcY,ζkX,ζkY,ζSc分别用ζ1,ζ2,ζ3,ζ4,ζ5,ζ6,ζ7表示。 铣削系统的协方差矩阵为

(18)

矩阵D是7阶正定对称矩阵。该矩阵有7个实特征值和7个线性无关的正交特征向量。

矩阵B的列向量由矩阵D的正则化特征向量构成。对铣削系统的随机向量X做正交变换[25]

X=BY

(19)

μY=BTμX

(20)

ζY=BTζX

(21)

极限状态函数可以表示为独立随机变量Y的函数[25]

Z=fX(X)=fX(BY)=fY(Y)

(22)

基于设计点法,变量Y的导数为[25]

(23)

Y*=BTμX

(24)

在空间Y中,Z=0是通过点Y*的极限状态切平面。根据独立随机变量线性组合的性质,可以得到Z的均值和标准差[25]

(25)

(26)

铣削系统的可靠性指标为[25]

(27)

定义变量Yi的敏感度系数为[25]

(28)

新Y*可以表示为[25]

Y*=μYi+βζYicosδYi

(29)

新X*可以表示为[25]

X*=BY*

(30)

设置误差为ε=10-6, 一直迭代直到2次迭代的偏差小于ε。将β值代入公式(29)可计算得到Y*的值。

铣削系统的可靠性概率定义为[25]

pr=1-Φ(-β)

(31)

式中，Φ(·)是标准正态分布的累积函数。

该工程区的大地构造单元为长江三角洲褶皱带中的景潭斑块褶皱束，由前震旦系变质岩组成。隧道的边坡坡度陡，地形陡峭。隧道位于地形的陡峭交交汇处。边坡围岩发育一组外部斜坡接头，在外部接缝面应力进行了重新分布并伴随着剪切位移及卸荷裂缝。边坡围岩地貌照片见图1。边坡围岩有一组外倾节理发育，沿节理面发生了应力剪切错动，并伴着应力重分布及卸荷裂隙。边坡主要软弱结构面发育照片见图2。隧道设计的本段围岩等级为Ⅴ级，支护类型为锚网喷护加钢拱架，断面结构类型为半明半暗，开挖方式为全断面，见图3。

4 应 用

4.1 整体叶盘侧铣加工实验

实验在五轴加工中心上进行。利用模态冲击锤(PCB 086C03)、加速度传感器(Kistler 8778A500)、振动信号采集卡(NI 9233)和分析软件(Cutpro V9.0)完成侧铣加工系统模态参数的识别,如图2所示。

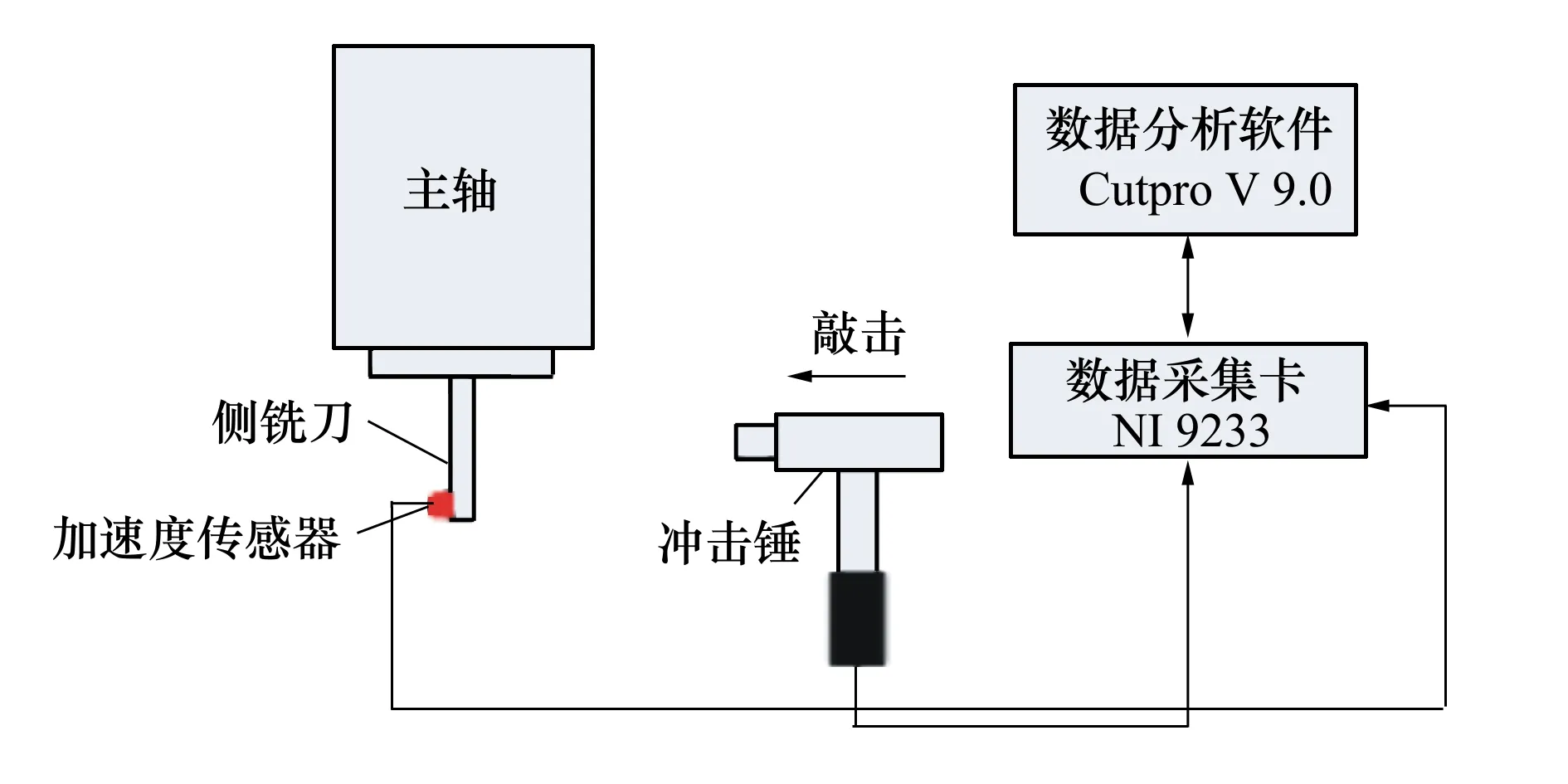
图2 振动信号采集过程

模态实验沿着侧铣刀的X和Y向进行。X,Y向的频响函数如图3和4所示。表1和2列出了X,Y向模态参数的多次实验测量结果。侧铣加工系统结构参数平均值和标准差计算结果如表3所示[27-28]。

图3 侧铣刀X向频响函数

图4 侧铣刀Y向频响函数

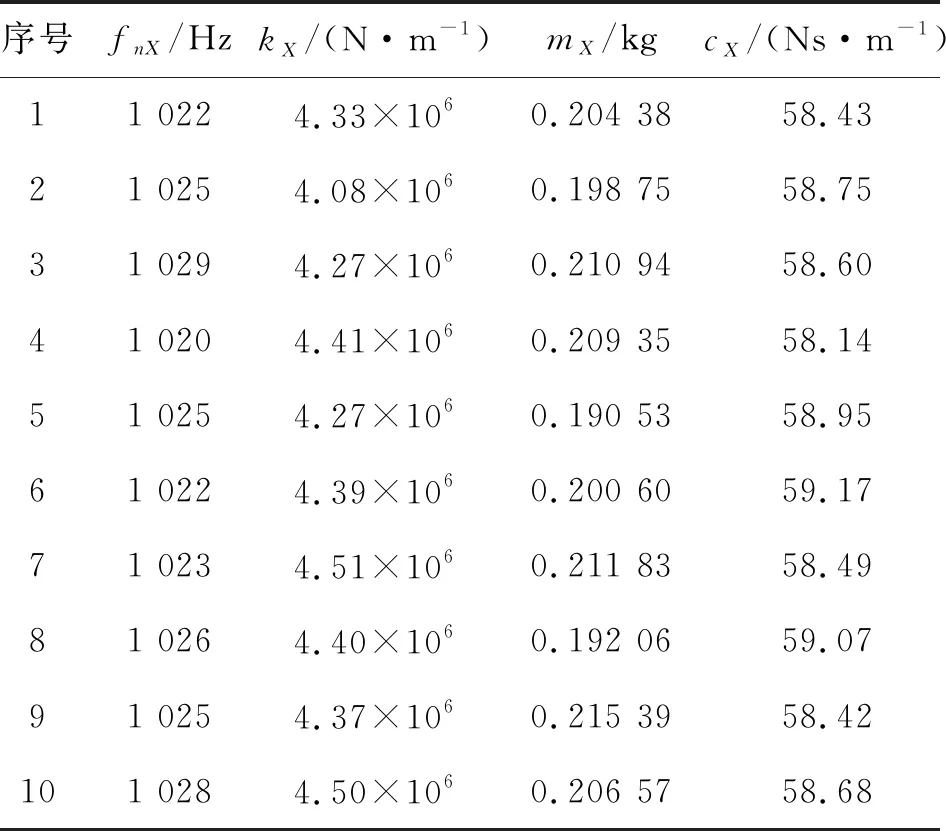
表1 侧铣刀X向模态参数测量值

表2 侧铣刀Y向模态参数测量值

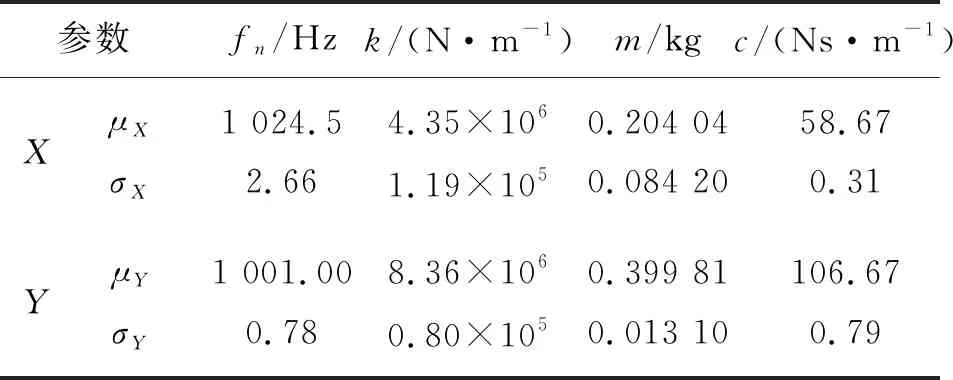
表3 侧铣刀模态参数平均值及标准差

4.2 侧铣颤振频率的分布

对于二自由度的侧铣加工系统,结构参数mX,mY,cX,cY,kX,kY取为实验测量结果的平均值。图5给出了侧铣加工系统的稳定性叶瓣图和颤振频率图,稳定性叶瓣图如黑色实线所示,颤振频率随主轴转速变化图如图蓝色点线所示。

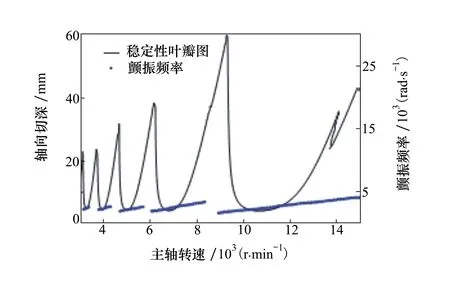
图5 侧铣加工系统稳定性叶瓣图与颤振频率图

4.3 侧铣加工系统的可靠度计算

侧铣加工系统稳定运行条件必须满足fX(X)<0。当已知切削深度时,侧铣加工系统的可靠度可由一次二阶矩法[24,26]和蒙特卡罗法得到。初始点设为侧铣加工系统随机变量平均值。一次二阶矩法和蒙特卡罗法得到的可靠度比较结果如表4所示。结果表明,一次二阶矩法的计算结果与蒙特卡罗法的计算结果吻合较好。相对误差最大的是7.43%。因此,一次二阶矩法可以应用于侧铣加工系统颤振可靠度的计算。

表4 给定切削深度主轴转速6 000 r/min的可靠度

4.4 可靠性叶瓣图

可靠度值设置为0.99。可靠性叶瓣图与稳定性叶瓣图对比如图6所示,黑色实线为稳定性叶瓣图,蓝色虚线为可靠性叶瓣图。蓝色虚线下方是可靠区域,可靠度大于0.99,蓝色虚线上方是不可靠区域,可靠度小于0.99。黑色实线下方与蓝色虚线上方的区域是稳定但不可靠区域,可靠度小于0.99。蓝色虚线下方的区域是即稳定又可靠的区域,可靠性大于0.99。黑色实线上方的区域是即不稳定也不可靠区域,可靠性小于0.99。

图6 侧铣加工系统稳定性与可靠性叶瓣图对比图

4.5 实验验证

侧铣验证实验在五轴加工中心上进行,主轴转速设置为6 000,8 000和14 000 r/min。切削深度为10～60 mm。当主轴转速为6 000 r/min,切削深度为20 mm时,加工表面光滑,可靠度值为0.999 86。当主轴转速为8 000 r/min,切削深度为20 mm时,加工表面呈波纹状,如图7所示,可靠度值趋近于0。

在可靠性叶瓣图上得到了关键可靠性值和极限可靠性值,如图8中的黑色圆点所示。当主轴转速为6 000 r/min,切削深度为26.6 mm时,可靠度为0.99,切削深度继续增加时,可靠度值下降,直到发生颤振,可靠度为零;当主轴转速为15 000 r/min,切削深度为36.8 mm时,可靠度为0.99,随着切削深度的增加,可靠度值会一直下降到零。验证实验的结果在图8中标出,五角形代表稳定点即无颤振发生,三角形代表不稳定点即发生颤振。实验结果与预测结果保持一致。实验结果表明可靠性叶瓣图可用于预测侧铣加工系统的稳定性概率。

图8 验证实验结果

5 结 论

本文建立了考虑随机变量影响的侧铣加工系统颤振可靠性预测模型。通过模态实验获得了侧铣加工系统X向和Y向的结构参数。利用结构参数的平均值绘制了侧铣加工系统的稳定性叶瓣图和颤振频率图。利用一次二阶矩法计算了侧铣加工系统的可靠性指标和可靠性概率,并与模特卡罗法的计算结果进行了对比。利用可靠性叶瓣图对侧铣加工系统的颤振区域与非颤振区域进行识别。可以得出以下结论:

1) 颤振频率是一个随机变量,它与结构参数m,c,k和主轴转速S有关;

2) 用一次二阶矩法和蒙特卡罗法对侧铣加工系统的可靠性概率计算结果具有较高的一致性。利用一次二阶矩法可以计算侧铣系统的可靠性概率。

3) 可靠性叶瓣图可较好地预测侧铣加工系统的颤振可靠性;可靠性叶瓣图可用于侧铣加工系统的稳定性概率估计。