基于双样条拟合的五轴插补算法

黎红石 樊留群 赵建华 黄云鹰

(①同济大学中德学院，上海200092；②沈阳机床(集团)设计研究院有限公司上海分公司，上海 200433)

五轴数控加工是获取高精度复杂曲面的有效手段之一，在船舶、汽车、航空航天等领域都有重要意义[1]，其中刀具路径规划则是保障加工质量的关键环节。常见的五轴加工采用单样条曲线进行插补[2]，利用微段平滑加工算法实现加工表面优化，但拟合算法无法区分三轴位置坐标和旋转轴角度信息，拟合得到的信息是位置和姿态互相影响的结果。双样条插补则提出将位于刀位文件中的刀尖点坐标与刀轴矢量分开，利用两条样条分别刻画这两类信息，以兼顾刀具在加工时位置和姿态两方面的表现[3-5]。除此还出现多样条的插补方法，来追求对加工路径更精确的控制[6]，但由此带来的计算量也会显著增加。本文借助于五轴加工标准测试样件S样件的刀位文件，采用文献[2]中的方法对数据点进行分段，针对其工件加工路径中采取单样条插补的数据点段，对其使用双样条插补，同时结合前瞻速度规划理论，实现完整的插补计算过程，再对插补结果进行分析对比，验证双样条插补的可行性和实用性。

1 刀位文件生成双样条曲线拟合方法的研究

1.1 双样条拟合

在现今五轴加工中，常使用的拟合工具为NURBS样条[7]。NURBS曲线主要由控制点和节点向量构成，样条拟合目标即控制点和节点向量的求解。双样条拟合则涉及到刀尖点和刀柄点两条样条的求解。

双样条拟合旨在从刀位文件里获取两条样条。每次循环从刀位文件中读取若干行数据，经过坐标变换。由刀尖点qm=(xm,ym,zm)组成第m个刀尖数据点Q(um)。结合刀轴矢量Om=(Oi,m,Oj,m,Ok,m)以及设定的刀柄长度Lt可以计算出一系列刀柄数据点q′(w)。至此得到刀尖点和刀柄点如图1所示。

1.2 控制点求解

曲线控制点求解方法采用带权因子和一阶导数约束的最小二乘逼近算法，详见文献[7]。

以刀尖点拟合为例，刀柄点曲线拟合与此相同。待拟合数据点qm(m=0，…，r)，其中每个数据点带有一阶导数约束，导数约束向量矩阵用Dm(m=0，…，r)表示。每个数据点qm和Dm都设置由一个称为权因子的参数进行控制，权因子是用来衡量曲线满足这项给出数据要求的严格程度，如数据点q3的权因子为0时，曲线就必须穿过q3，类似插值。权因子常见取1。

数据点qm和Dm以权因子为判定标准，分为完全约束(权因子为0)和非完全约束(权因子不为0)。参与方程计算的各个矩阵：S表示非完全约束的数据；T表示完全约束的数据；W=[wk]为对角阵，对角线上记录没有完全约束时对应的数据权因子值；P=[Pk]为控制点；N记录非完全约束的数据项的基函数或基函数一阶导数信息；M记录完全约束的数据项的基函数或基函数一阶导数信息；

接下来引入拉格朗日乘子A=[λk]，k=0，…，mC，然后列出方程。

在满足完全约束方程MP=T的情况下，需要时非完全约束方程NP=S等号两边误差最小，即S-NP最小。利用A=[λk]，即需要式(1)达到最小：

(ST-PTNT)W(S-NP)+aT(MP-T)

(1)

将其求导并令导数为0，结合MP=T，可以计算出控制点P=[Pk]。

1.3 节点向量求解

同样以刀尖点数据为例，要获得节点向量，需要先将数据点参数化，参数化的方法有很多：均匀参数化、弦长参数化和向心参数化等[7]。本文采用弦长参数化：

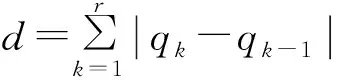
(2)

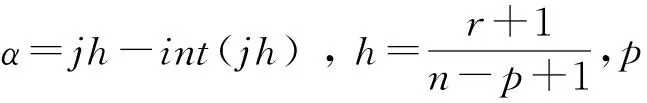
至此可以计算出刀尖点C(u)和刀柄点C′(u)拟合曲线的控制点和节点向量P、U，P′、u′。

2 双样条曲线插补研究

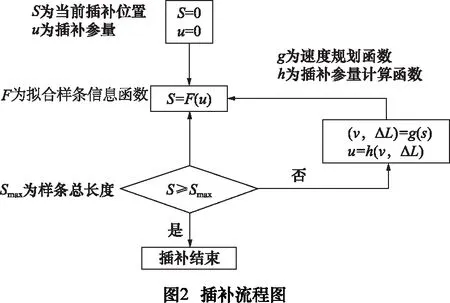
利用曲线拟合得到的双样条，采用图2的步骤进行插补。

2.1 曲线插补原理

双样条曲线插补需要求得刀尖点样条的参量uj+1和刀柄点样条的参量wj+1，插补过程以刀尖点曲线为插补路径，将其作为主要插补规划对象，故首先计算刀尖点的参量uj+1。常见的曲线参量计算方法有等参数法、泰勒展开式、四阶Adams方法、预测-校正方法[8],本文采用四阶Runge-Kutta法进行参量计算[9]。应用到NURBS插补表现为：

(3)

式中:ΔL为一个插补周期中规划的步长

除了后续教育，澳大利亚对资产评估培养中最大的特点在于其更加注重高等教育。缺乏扎实的基础的资产评估从业人员在资产评估业务活动中是致命的，会影响了资产评估人员的就职上限。所以澳大利亚各类高校基本都开设了资产评估相关课程并拥有一套完整的高等教育体系。这类体系对资产评估人才的培养有益无害，澳大利亚的资产评估人员只要在大学获得相关学位并拥有2年相关工作经验后就可以直接申请成为资产评估师，并不需要通过资产评估师考试。

于是

(4)

2.2 插补参量同步

得到刀尖点样条的插补参量uj+1后，需要计算此时刀柄点曲线上的插补点，即确定刀柄点曲线的参量wj+1。为了能从拟合的双样条上正确选取反映刀轴矢量原始走向的刀柄点和刀尖点，需要完成插补参量的同步如图3。常用的同步方法[10]为，当uj+1处于刀尖点曲线节点向量区间[uk,uk+1]时，对应的wj+1也应处于刀柄点曲线节点向量区间[wk,wk+1]。

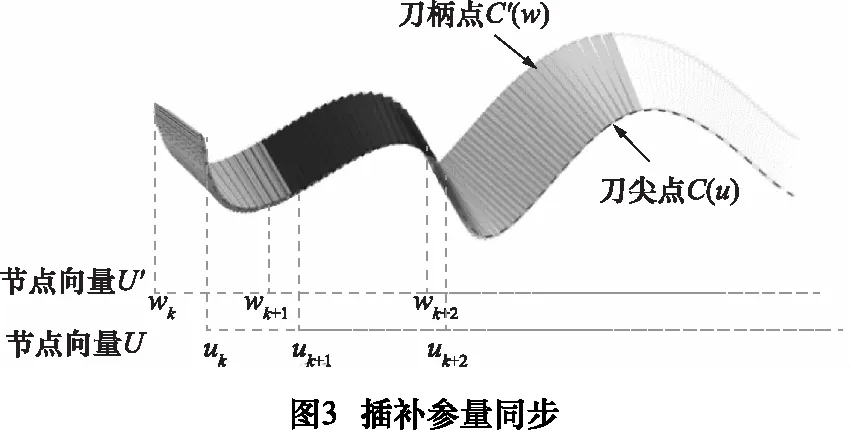
在保证两条样条的参量始终处于同一角标的节点区间后，可以定义区间内参量uj+1与wj+1的对应关系，一般以其线性变化关系建立等比关系式如式(5)：

(5)

3 前瞻速度规划

在双样条插补过程中，为了保证刀具的运动特性良好、减缓机床振动和改善工件质量，也同样会面临速度规划的问题。前瞻速度规划指在动态缓冲区预读若干程序段，获得多根样条的点位信息，提前计算是否存在危险点并在发现时为其分配速度，以此确定出各个速度节点，形成速度分段。然后按给定的速度曲线计算段内的加减速情况，完成每一个插补点的步长计算，从而为插补器提供信息，并在有新的拟合样条信息加入缓冲区时进行刷新，更新各节点给定的速度[11-12]。其中段内加减速采用S曲线加减速规划图[13]。

以整体加速过程为例， 即vs≤ve，需要计算两个临界距离，一个是按照上述S型曲线加减速图从vs加速到最大速度从F再减速到ve的距离Rmaxl，一个是直接从vs加速到ve的距离Rminl，然后与该段本身相距长度D进行比较，情况如下：

(1)D>Rmaxl：则速度规划为，从vs加速到最大速度F，然后以F匀速加工D-Rmaxl长度，再减速到ve；

(2)Rminl≤D≤Rmaxl：此时刀具无法做到加速到最大速度F再减速，但又有过于充足的距离加速到ve，便根据节点间距离D的大小反算得到一个中间速度vtemp，通过加速到vtemp再减速到ve来实现最大加工效率。但值得注意的是，vtemp的大小需要保证vs到vtemp的加速段长和vtemp到ve的减速段长大于插补周期T内按照S型加减速该位置对应的插补步长ΔL，否则插补时得到的插补点会越过该中间速度点。

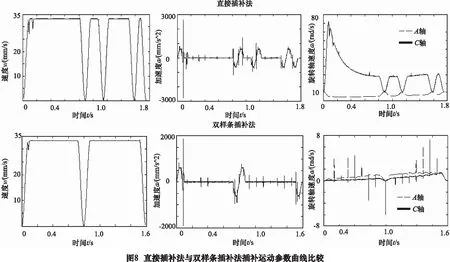
(3)D

减速过程同理，计算两个临界距离，也有3种规划情况。

完成速度规划之后，通过计算起始点到当前插补点的弧长来确定该点在速度规划里的位置，从而获得对应的速度。但由于本文是采用Runge-Kutta法求解插补参量的，公式中不是直接使用瞬时速度，而是一个插补周期T内的步长ΔL，即速度图上当前点向后一个T时间范围走过的面积。

所以在给定一个参量uj后，按照速度规划的结果，得到的是一个步长ΔLj。但到现在为止速度规划仅考虑了单条样条的插补情况，反映在五轴加工上即只顾及了刀尖点qm=(xm,ym,zm)的运动状态。于是在实时获得ΔLj且计算出uj+1后，还需要利用式(5)得到刀柄曲线wj和wj+1，分别计算出C(uj)、C′(wj)以及C(uj+1)、C′(wj+1)。并结合C(uj-1)、C′(wj-1)来计算刀轴矢量A(uj)变化的速度和加速度如图4。

(6)

如果求得的速度和加速度满足最大角速度、角加速度约束，则ΔLj可以使用，否则按照最大角速度、角加速度约束反解允许的最大步长ΔLjmax，然后再利用式(3)求插补参量uj+1。

4 实验结果与分析

实验采用S样件的刀位文件，利用最小二乘法，分别对直接插补 (利用坐标变换前X,Y,Z,A,C形成的五维向量作为原始点) 和双样条插补进行拟合。得到结果图5～7。

从结果图中可以看出，S样件的数据点中会出现刀轴矢量突变的情况，采用平移坐标和旋转坐标合并的直接插补法拟合，矢量拟合误差小，但会沿袭这样的曲线特性；而采用双样条插补的计算方法进行拟合，会填补刀轴矢量使其平滑过渡，但拟合误差会增大。

插补过程中，采用参数：插补周期T=1 ms、最大进给速度F=2 000 mm/min、最大加速度为a=600 mm/s2、最大加加速度J=20 000 mm/s3、最大弦高误差error=0.01 mm。插补结果如图8。

在两种插补方法中，实验数据点被分为了三段进行拟合，在采用相同的速度规划策略的前提下，直接插补法在样条内部会多产生几个危险点，使其最终插补速度曲线呈现多次加减速；双样条插补也因平均速度更大，整个插补所用时间也更短。从加速度曲线来看，双样条插补能保证所有点的加速度都满足最大加速度要求且波动次数更少。最后旋转轴速度运动表现上，也如同拟合结果分析的那样，双样条插补的旋转轴速度过渡更平滑。

5 结语

本文对五轴加工中双样条插补的整个计算过程进行了仿真模拟，并将其与常见的直接样条插补法进行了比较。两种插补方法均采用相同的最小二乘拟合方法以及S型曲线速度规划，从模拟结果数据可以看出，双样条插补与直接插补法在刀尖点的拟合精度上差别不大，但在刀轴矢量上，双样条插补牺牲了一定的拟合精度。但不管是刀尖点还是旋转轴，双样条插补得到的运动参数曲线表现都更出色。在五轴加工中，根据原始点数据信息和机床自身特性，可以适当采取不同的插补方法，双样条插补不失为不错的选择之一。