隔振器组合系统稳态振动特性研究

洪鹤庭，孙红春

（1.宁夏理工学院，宁夏石嘴山 753000；2.东北大学机械与自动化学院，沈阳 110819）

0 引言

随着社会的发展与进步，生活与工程中的振动现象越来越普遍，振动不仅影响设备的工作精度、加剧构件磨损、引起结构疲劳破坏、还会对操作工人的身体健康造成极大影响[1]。其对设备的影响主要表现在两个方面：一是在某激振频率下，设备产生共振，其响应值超过设备的限定值而导致其本身结构的损坏或降低其效率；二是长期的振动引起设备的疲劳破坏[2]。因此有效地隔离振动是现代工业中非常重要的问题。

目前，减小振动与冲击的危害主要有3 个途径。一是减小或消除振动源的激励。例如，改善机构或设备的平衡性能，提供机构设备的动、静平衡要求；对具有较大辐射表面的薄壁结构涂以阻尼层，以减弱声音激励引起的振动。二是防止系统共振。例如改变系统固有频率，防止扰动特性与共振特性的不良耦合。三是采用隔振器或其他隔振设施以减小振动的传递。

1 工程应用

目前，随着振动冲击的危害逐渐加深，目前国内外已经研究出成百上千种产品。例如国外学者所研究的HLSDS隔振器[3]，广泛应用于汽车领域，并且具有良好的隔振效果。如图1所示，国内某公司所生产的高性能隔振器广泛应用于地铁、桥梁房屋、普通机电设备（如：压力机、振动筛、风机、发动机组等）。其在舰艇上尤为重要，在舰艇上，许多电机都安装了橡胶减震器来隔振，大型电机更是直接安装在减振浮筏上；装舰的电子设备基本上都安装了各种隔振器以防止振动所带来的危害，这样当发射或遭到攻击时，才能为电子设备提供足够的保护。

图1 传统隔振器

2 原理描述

针对一般的弹簧减震器存在自振现象、阻尼比太小、对于共振频率附近的振动隔离能力较差、橡胶隔振器易老化、产生蠕变、气垫隔振器价格过于昂贵等缺点，设计了一款新型隔振器组合系统，既能够解决低频段隔振，又能够增加其阻尼，还不易老化且价格低廉。

本隔振器组合系统通过基座、缓冲、质量块和钢丝绳隔振器连接成为一个整体。其中，由质量块M和弹簧ks组成的系统为主系统[4]。为了拓宽系统的工作频率范围，同时使主系统的振动减少到最低，设计了由可调节质量块m、弹簧ke、弹簧kt和黏性阻尼器c组成的系统。可以看出，在传统的有阻尼动力减振器的基础上，在质量块和基座之间增加了一根负刚度弹簧和一个黏性阻尼器，能够消除一些在较宽激振频率范围工作设备的振动。

3 问题简化与建模

通常将隔振对象看成质量—弹簧—阻尼3元素构成的单自由度系统，而实际工程中的隔振对象远比此复杂。考虑如图1（a）所示的系统，由质量m1和弹簧k1组成的系统为主系统，由质量块m2、弹簧k2和阻尼器c组成的系统为分系统，所构成的为传统有阻尼动力减振器。

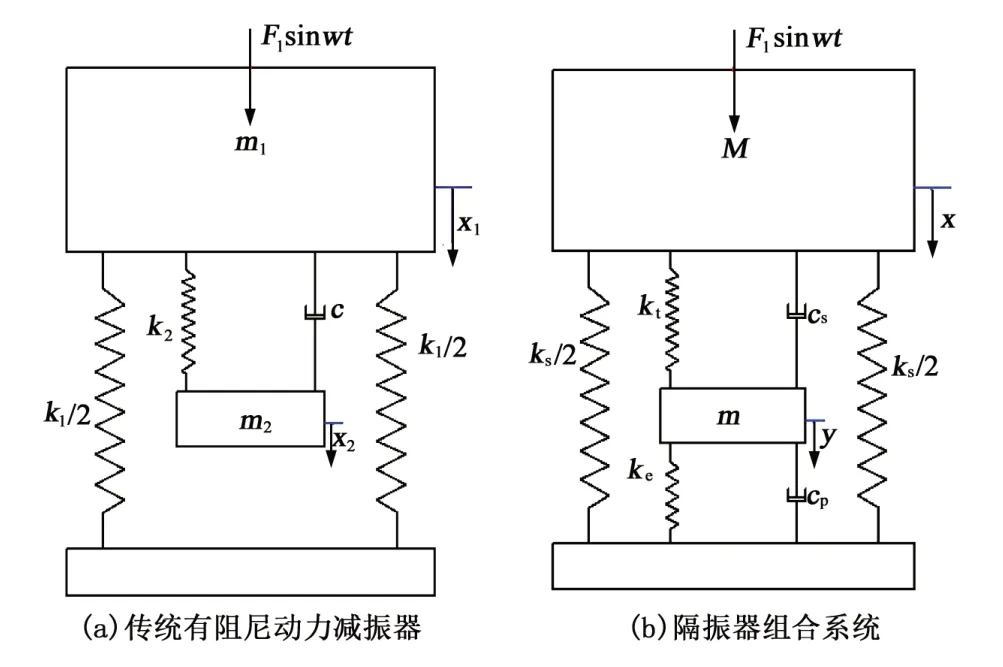
图2 两种隔振器对比图

目前，关于隔振器系统的最优设计方法都是以单自由度系统为对象。由图1（b）所示系统可以看出，为了使系统的隔振能力最大化，在传统有阻尼动力减振器的基础上，在可调节质量块和基座之间增加了一根负刚性弹簧和一个黏性阻尼器c，建立简化的隔振系统模型。

根据图1（b），应用牛顿定律可建立隔振器组合系统的振动微分方程为（此处用复量表示法，以F1eiwt为方程激励F1sinwt）：

4 计算与分析

设稳态响应为：

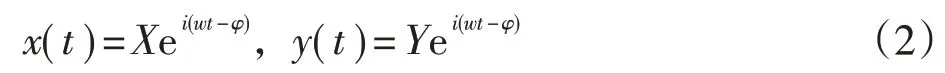
将式（2）代入式（1）得到：

可得相应的频率方程为：

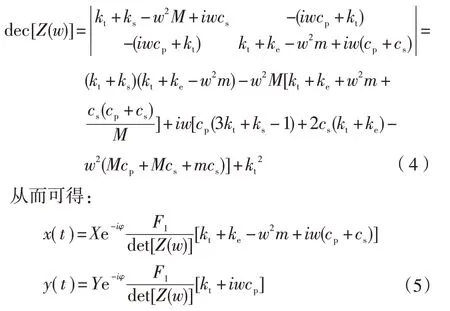
因而可解出稳态响应幅值为：

由于振动源的力在此处通过弹簧和阻尼器传递给质量块，这些力为：

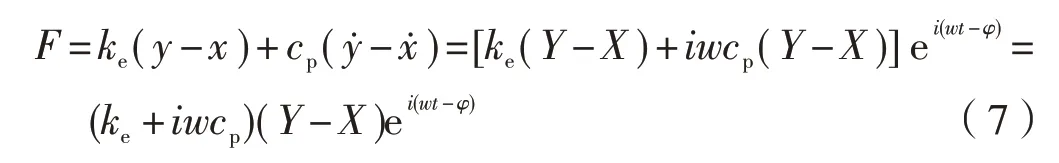
故传递力的幅值为：

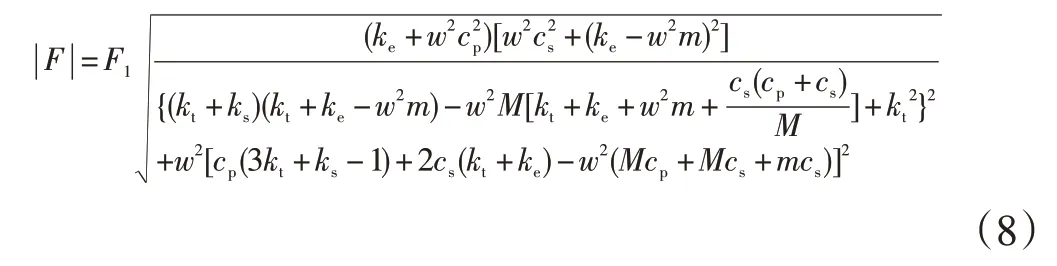
则实际传递力的幅值与激励幅值之比，即传递率为：

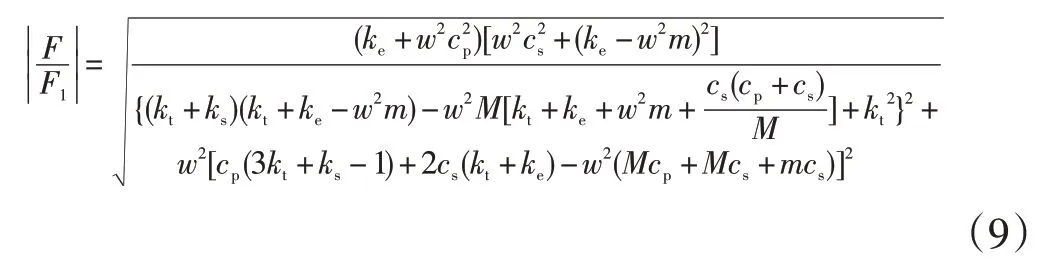
根据Roth-Hurwitz 稳定性判据[5]，必须保证其各项系数全部为正，且其顺序主子式全部大于0，才能使隔振器组合系统的固有频率不会出现负值，系统稳定。同时设备的重量一般不得超过隔振系统所能承受总载荷的80%。

明显可以看出，在保证隔振器组合系统工作条件的情况下，传递率永远小于1，即安装了隔振器组合系统的设备所承受的振动冲击远小于没有安装隔振器组合系统设备所承受的振动冲击。

5 计算与分析

5.1 算例分析

已知隔振器系统的最大正压力P=9 800 N，均匀分布，其材料选择为60Si2Mn，材料的弹性模量为210 GPa，泊松比为0.3，质量密度为7 900 kg/m，材料的屈服强度约为1 175 MPa。

5.2 数值计算验证

通过Simulation-express，首先对隔振器组合系统模型进行六面体网络划分，为保证与现实工程运用最大化相似，固定其底面，在载物板上施加9 800 N的均匀分布力，第一次仿真模拟中采用了如图2（a）所示的传统有阻尼动力隔振器对其进行静应力分析，其静应力—位移结果如图3所示。可以看出，在9 800 N的均布压力下，载物板位移量为0.468 0 mm，其最大等效应力为414 MPa，在两侧弹簧处承受的力最大，其产生的应变也较大。

图3 传统有阻尼动力隔振器静应力—位移云图

图4 隔振器组合系统静应力—位移云图

在第二次实验中，不改变测试力和其他参数的条件下，采用图2（b）中所设计的隔振器组合系统进行建模，为了分析新结构与传统结构对隔离性能的影响，在设置隔振器参数时采用了最优阻尼比，得到的静应力—位移结果如图4 所示。可以看出，在9 800 N 的均布压力下，载物板位移量为0.466 2 mm，其最大等效应力为410 MPa，相对传统隔振器，其静应力作用下的位移量与最大等效应力均有所下降，基于此，为了确保所设计系统的动态特性，还对隔振器组合系统进行了无规则振动下的线性动态分析，结果如图5所示。可以看出，本文所设计的隔振器组合系统在不同频率下均有着优良的动态性能，相比传统有阻尼动力隔振器在各项指数上均有所提升。

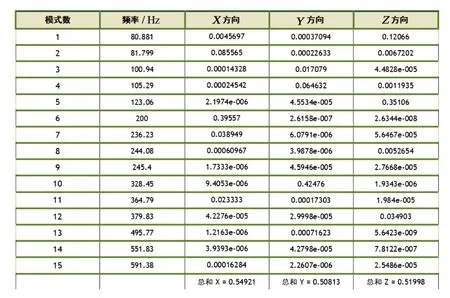
图5 隔振器组合系统线性动态分析

6 结束语

通过使用硅锰弹簧钢60Si2Mn制作隔振器组合系统，并选用合适的方式进行布置，使用Solidworks建模，并运用Simulation-express 进行隔振系统的有限元模型[6]可以发现，在隔振器组合系统的作用下，在一定频率范围内共振峰值有明显减弱，并且在设计频率范围内能达到最优隔振效果。在实际工程应用中，在已经选择好隔振器制作材料的条件下，如何将其组合起来形成隔振效果最大化是一个难题，本文已经提出一种有效组合系统的方法，并对其进行了建模与仿真测试，证明了其有效性。但须注意的是，设计人员还需考虑如何满足质量快大振幅要求以及弹簧元件的疲劳等问题，才能更好地在工程中应用。