轨道检测中角速度与加速度测量法误差分析
2021-03-01陈仕明秦哲杨爱红魏世斌
陈仕明,秦哲,杨爱红,魏世斌
(1.中国铁道科学研究院研究生部,北京 100081;2.中国铁道科学研究院集团有限公司 基础设施检测研究所,北京 100081)
0 引言
良好的轨道平顺性是保证列车安全运行的前提。高低不平顺会影响车体的垂向加速度和轮重减载率;轨向不平顺会影响车体的横向加速度和脱轨系数,进而威胁行车安全。目前,国内外常采用弦测法和惯性基准法测量轨道的高低及轨向不平顺。其中,弦测法存在测量结果明显失真的缺点,不能直接反应轨道形变;惯性基准法将惯性传感器和测距传感器的数据融合处理,可以较真实地反映轨道不平顺情况[1]。
在铁路线路中,轨道不平顺波长范围较宽,30~150 m波段多由路基工后沉降不均、路基施工高程偏差以及跨度较大的桥梁动扰度等形成;150 m以上波段多由地形起伏、线路坡度变化等形成。采用惯性基准法检测时,必须提高伺服加速度传感器的精度及滤波部分的性能,以保证在增大可测波长范围时,幅值、分辨率精度仍符合要求,波形失真较小。另外,需要进行剔除线路坡度、曲线曲率变化等影响的处理,才能得到符合实际情况的长波不平顺数据。
陀螺仪测量是轨检小车静态相对测量的主要方式[2]。邢宗义等[3-5]讨论了采用安装在构架上的陀螺仪测量不平顺的方法;Westeon等[6-7]指出陀螺仪测量对短波不平顺存在一定衰减,在低速条件下陀螺仪测量的效果优于加速度计。以上文献仅对比了不同测量方式的测量结果,并未从理论上对比其造成的误差。受传感器噪声和地球自转的干扰,高精度光纤陀螺仪(FOG)会产生低频漂移;加速度计受检测梁振动影响较大,会产生大量高频噪声。研究推导2种测量方式的算法,从理论上分析可能产生的误差,以及测量精度与传感器分辨率、噪声系数之间的关系。
1 测量算法
1.1 加速度测量法
根据相关测量原理,轨道的高低不平顺和轨向不平顺具有一致性,可选择高低不平顺为测量对象,介绍其测量算法。加速度测量法原理示意见图1。

图1 加速度测量法原理示意图
安装在转向架上的垂向加速度计可提供检测梁的垂向运动信息;安装在检测梁上的激光摄像组件可提供检测梁与轨面的垂向/横向位移变化值。加速度测量法可用公式表示为:
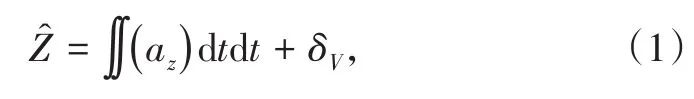
式中:aZ为加速度计测量的垂向加速度;δv为激光摄像组件测量的垂向位移变化。
1.2 角速度测量法
角速度测量法垂向坐标示意见图2,相应的轨道高低不平顺估计值为:


图2 角速度测量法垂向坐标示意图
式中:φ为水平基准面与轨面切线方向的夹角(轨面倾角);φ̇为轨面倾角的一阶微分。
由式(2)可知,高低不平顺可认为是对角度φ的空间步长的一阶积分,也可转换为采样所得点头角速度的时域信号与列车前进速度的二次积分。
2 传感器分析
2.1 实测数据分析
对实际传感器采集的垂向加速度计、点头陀螺仪的数据进行频谱分析,采用Welch法并选用矩形窗函数,选取某高铁线路列车时速140 km时的传感器实测数据为分析对象,传感器实测数据分析示意见图3。CRH5的转向架垂向固有频率为7.45 Hz,则时速140 km对应敏感波长约5.2 m。由图3(a)可知,PSD曲线在4.683 0 m存在1个峰值,为转向架与轨道不平顺输入激励共振产生;在32.900 0 m存在1个峰值,为该线路中的32 m波长不平顺产生;在0.629 5 m处存在1个峰值,且高达0.086 77g2/m,可能为加速度传感器高频噪声,应通过传感器数据预处理将该频段信号滤除。
点头角速度峰值位置与加速度计类似。对于基于惯性基准法的加速度计,在0.62 m处的有害信号会对不平顺测量带来较大干扰。该高频噪声主要由转向架振动和电磁环境引起的,可视为白噪声。
由图3b可知,当列车自振频率与轨道输入激励接近时,相对于加速度计,陀螺仪在1.0 m波长以下高频分量的功率谱密度较小,说明陀螺仪受车体高频振动影响较低。同时,检测梁的点头动态响应范围与轨道倾角变化的动态范围较接近,对于长波长不平顺信号反应明显。因此,将滤波器截止波长提升至1.5 m,可有效对振动产生的传感器噪声进行衰减,且不影响不平顺信号的参数估计,有效提升了信噪比。

图3 传感器实测数据分析示意图
2.2 传感器选型
用正弦函数表示线路中的轨道不平顺:
式中:A为幅值;v为列车行驶速度;λ为波长。
理论上加速度计的敏感信号为:
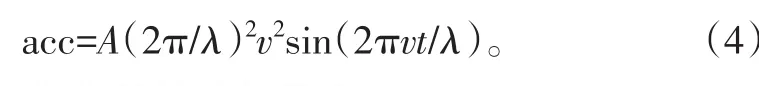
理论上陀螺仪的敏感信号为:

假设A为1 mm,根据式(3)—式(5),整理得到不同波长的不平顺测量对应的惯组理论值(见表1)。
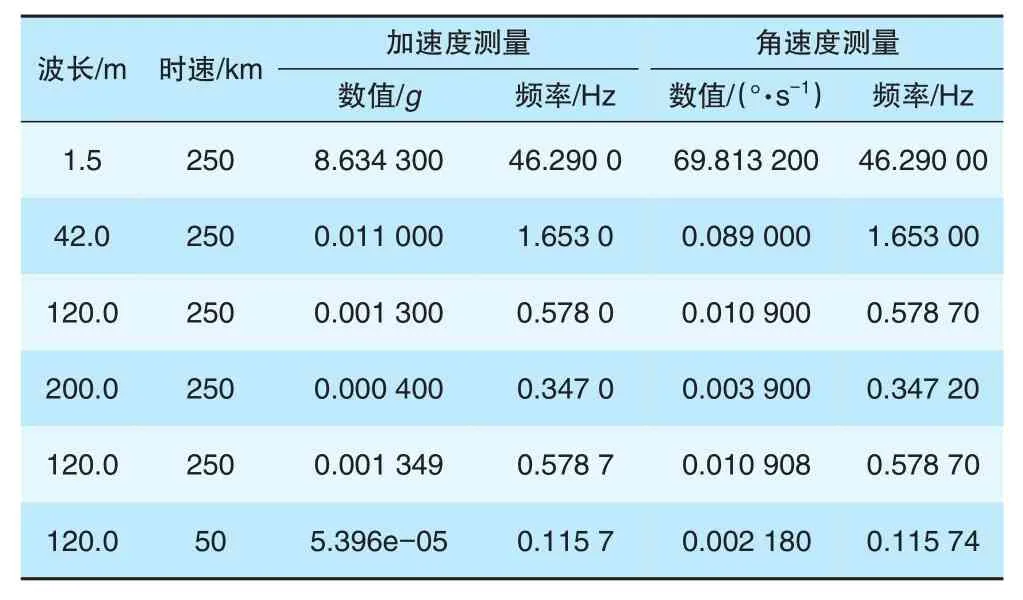
表1 不同波长的不平顺测量对应的惯组理论值
选取2种典型情况,当列车以时速250 km行驶,波长为1.5 m时,惯组理论值最大;当列车以时速50 km行驶,波长为120 m时,惯组理论值最小。
综上所述,惯性测量要求加速度计动态范围达1.6×105m/s2以上,要求陀螺仪动态范围达3.2×104°/s以上。若要求列车在低速下(时速50 km)测量精度达到1 mm以内,则加速度计的分辨率和精度要高于5×10-5(g·m/s2)以上,陀螺仪的分辨率和精度要高于1×10-3°/s以上。同时根据式(3)—式(5)可知,加速度计数据受速度影响比陀螺仪大。因此,在低速情况下,加速度计信号衰减更明显。
3 噪声分析对比
陀螺仪、加速度计和其他传感器的零偏都可以在初始校准期间归零,但零偏会随着时间产生漂移。这主要是由温度变化造成,也可能是电源电压变化、环境因素、材料老化等因素造成。当前采用的光纤陀螺仪零偏稳定性指标为1°/h(100 s平滑),加速度零偏稳定性为1 mg。Allan方差分析法是常用的误差分析法,可综合分析陀螺仪性能并得到各项静态误差指标[8]。光纤陀螺仪Allan方差结果见图4。

图4 光纤陀螺仪Allan方差结果
如图4所示,对陀螺仪的随机误差进行Allan方差标定,得到惯组的零偏不稳定性σB为0.018 6°/h、速度随机游走σK为0.005 3°/h3/2、角度随机游走σN为0.001 2 °/h1/2。
导致陀螺仪长期漂移误差的零偏不稳定性和角速度随机游走成为影响惯性测量系统性能的主要因素,因此陀螺仪随机误差可近似表示为角度随机游走与角速度随机游走之和[9]。对光纤陀螺仪的随机噪声建模,为便于分析,将随机误差所示为时间t的函数:
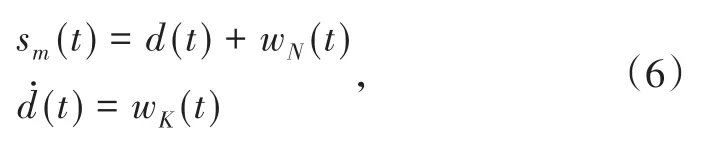
式中:sm为陀螺随机误差;wK与wN为零均值的白噪声;d(t)为随机游走误差分量;ḋ(t)为d(t)的一阶微分。其统计特性为:

式中:τ为时间;σK为噪声wK的标准差;σN为噪声wN的标准差;δ()为狄拉克函数。
利用Allan方差分析加速度计的方式与陀螺仪一致,不再赘述。参考文献[10]可分析陀螺仪噪声系数(角度随机游走、角速度随机游走)对于测量结果的影响,根据式(1)、式(2)可得加速度计和陀螺仪的噪声系数对测量结果的影响(见表2—表3)。
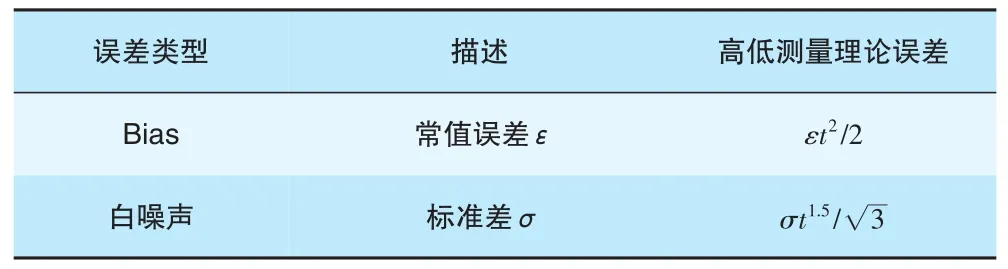
表2 加速度计噪声系数对测量结果的影响

表3 陀螺仪噪声系数对测量结果的影响
由表1可知,角速度测量法的误差与速度有关,其误差随速度线性增长,并且角速度随机游走产生的低频漂移是陀螺仪的主要误差,随时间增长最快。
当前轨道测量系统采用的高精度惯性器件包含光纤陀螺仪与加速度计。实际上,陀螺仪的输出常以白噪声为主。在这种情况下,σ100s与σN之间的关系近似为:

光纤陀螺仪的零偏稳定性指标为1°/h(100 s平滑),那么对应的σN近似为系统采样率°h(0.001°/s)。同理,加速度计的零偏稳定性指标为10-4g,对应的σN近似为1.667×10-5g,则离散白噪声的标准差为3.727×10-4g。由表1可知,当列车以时速50 km测量幅值为1 mm的120 m长波时,理论上陀螺仪的测量信噪高于加速度计的测量信噪比。为500 Hz,则离散白噪声的标准差为3.726 8
4 结论
基于加速度和角速度测量法,以高低不平顺测量为例,分析传感器噪声系数、不平顺波长、行车速度对于测量结果的影响,得到以下结论:
(1)相对于加速度计,高精度陀螺仪受列车振动的影响更小、动态响应更小。因此,当列车高速行驶时,加速度传感器信号更加明显,相比于角速度测量有一定优势。
(2)通过对传感器标定发现,当列车低速行驶时,角速度测量结果在理论上更准确、信噪比更高。
(3)当线路中存在较多长波不平顺时,角速度测量法得到的信号更明显,能更真实地反映轨道不平顺情况。
