Flow structures, nonlinear inertial waves and energy transfer in rotating spheres

Tinyi Li , b , Minping Wn , , , Shiyi Chen , b , ,

a Guangdong Provincial Key Laboratory of Turbulence Research and Applications, Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, China

b State Key Laboratory for Turbulence and Complex Systems, College of Engineering, Peking University, Beijing 100871, China

c Southern Marine Science and Engineering Guangdong Laboratory (Guangzhou), Guangzhou 511458, China

Keywords: Rotating turbulence Spherical confinement Helical-wave deomposition Inertial wave

ABSTRACT We investigate flow structures, nonlinear inertial waves and energy transfer in a rotating fluid sphere, using a Galerkin spectral method based on helical-wave decomposition (HWD).Numerical simulations of flows in a sphere are performed with different system rotation rates, where a large-scale forcing is em- ployed.For the case without system rotation, the intense vortex structures are tube-like.When a weak rotation is introduced, small-scale structures are reduced and vortex tubes tend to align with the rotation axis.As the rotation rate increases, a large-scale anticyclonic vortex structure is formed near the rotation axis.The structure is shown to be led by certain geostrophic modes.When the rotation rate further in- creases, a cyclone and an anticyclone emerge from the top and bottom of the boundary, respectively, where two quasi-geostrophic equatorially symmetric inertial waves dominate the flow.Based on HWD, effects of spherical confinement on rotating turbulence are systematically studied.It is found that the forward cascade becomes weaker as the rotation increases.When the rotation rate becomes larger than some critical value, dual energy cascades emerge, with an inverse cascade at large scales and a forward cascade at small scales.Finally, the flow behavior near the boundary is studied, where the average bound- ary layer thickness gets smaller when system rotation increases.The flow behavior in the boundary layer is closely related to the interior flow structures, which create significant mass flux between the boundary layer and the interior fluid through Ekman pumping.

Rotating turbulence subjected to confinement is common in en- gineering, geophysical and astrophysical applications [1,2] .Inertial waves are efficient in energy transport in a rotating fluid [3,4] .Phillips [5] discussed the reflection of inertial waves from a rigid plane surface in a uniformly rotating fluid, which provides a mech- anism of energy transfer among different wavenumbers.He also derived an approximate solution of the radiative equilibrium re- sulted from repeated reflections of inertial waves in a large rotat- ing box of general shape.Ibbetson and Tritton [6] interpreted their experimental results of decaying turbulence under rotation by con- sidering that inertial waves carry energy to the dissipative bound- ary layer.Morize and his co-workers performed a series of exper- iments of decaying grid-generated turbulence in a rotating tank.They concluded that the confinement results in a decrease of vor- ticity skewness at larger times [7] and explained the experimental decay exponents by a phenomenological model considering the ef- fects of rotation and confinement [8] .

Moreover, the confinement can also change the structure of tur- bulence.Hopfinger et al.[9] investigated turbulence produced by an oscillating grid in a rotating tank and found persistent vortex structures with axes parallel to the rotation axis under the simul- taneous action of local forcing, system rotation and confinement.Godeferd and Lollini [10] performed direct numerical simulations and showed that the wall produced organized structures through Ekman pumping.Bewley et al.[11] investigated the grid turbulence in both square channels and circular cylinders under rotation.They observed large-scale inertial waves resulting in inhomogeneity of the system, which resonate at frequencies depending on the ge- ometry of the container.

Many geophysical and astrophysical bodies can be considered as rotating spheres, wherein inertial waves and oscillations are ubiquitous and strongly affect the fluid dynamics.Besides, thermo- chemical convection and magnetic forces complicate the dynam- ics in the cores of terrestrial-type planets [12,13] .Guervilly and Cardin [14] and Kaplan et al.[15] studied the nonlinear convec- tion in a rapidly rotating sphere for smallPrby a quasi-geostrophic model and fully 3D direct numerical simulations, respectively.Both of them found the subcriticality of convection at lower Ekman numbers [16] .Lam et al.[17] numerically investigated the nonlin- ear thermal inertial waves in rotating spheres with small Prandtl numberPrand their results are consistent with the asymptotic theory [18,19] .At moderately supercritical Rayleigh numbers, they revealed that various thermal-inertial-wave modes are nonlinearly interactive and then leads a weakly turbulent state.

Many investigations of rotating fluid spheres are devoted to understand planetary magnetism (see Ref.[20] for review).For magnetoconvection [21] where there is an imposed magnetic field, Olson and Glatzmaier [22] numerically studied the nonlinear thermal-convection structure in a rotating spherical shell of electri- cally conducting fluid.They found that for Elsasser numbersΛ≥1 there exists magnetostrophic flow inside the inner-core tangent cylinder and large-scale spiralling geostrophic flow outside.With regard to self-consistent magnetohydrodynamic (MHD) dynamos, which are of great significance to understand planetary magnetism, Gilman and Miller [23] first simulated a self-consistent convective hydromagnetic dynamo in a rotating spherical shell, which behaves differently than the solar dynamo.Mininni and his co-workers solved the incompressible MHD equations in spherical geometry with [24] and without rigid rotation [25] .They oberved sponta- neous flips of the dipole orientation in the non-rotating dynamo cases, as well as strong fluctuations of magnetic energy levels and turbulent magnetic dipole behaviors in the rotating dynamo cases.

In the present study, we focus on flow structures and nonlin- early interacting inertial waves of forced turbulence in rotating fluid spheres, where a large-scale external force is added as the generation mechanism of turbulence.Zhang et al.[26] first found explicit general analytical expressions of inertial waves in a rotat- ing fluid sphere (see also Ref.[27]).Canet et al.[28] performed numerical simulations and identified the classes of hydromagnetic quasi-geostrophic modes in rapidly rotating planetary cores.Maffei et al.[29] studied the columnar inertial modes in rapidly rotating spheres and spheroids using the quasi-geostrophic (QG) assump- tion.However, flow structures and nonlinear inertial waves in ro- tating spheres are relatively less investigated, especially for turbu- lent states.In this work, we address the following questions: What do the flow structures look like for different system rotation rates? Which inertial waves are responsible for the flow structures? How does the nonlinear energy transfer change compared with the case without spherical confinement? What is the flow pattern near the no-slip boundary?

In the present study, we consider a fluid sphere of radiusrowith kinematic viscosityνand the rotation vectorΩ=Ωez, whereezdenotes a unit vector in thez-direction.The governing equations in a rotating coordinate frame are

whereuis the velocity vector,pis the modified pressure incorpo- rating a centrifugal term andfis the body force that drives the system.We adopt a spherical polar coordinate(r,θ,φ)with unit vectorsThe no-slip boundary condition is used, which is relevant to liquid metal cores of terrestrial planets.

In the present study, we adopt a Galerkin spectral method based on helical-wave decomposition (HWD) to simulate flows in a sphere.This method was developed by Liao and Su [30] who ex- tended the previous HWD-based spectral method [24,25,31] with a series of auxiliary fields for the implementation of no-slip bound- ary condition and a dealiased pseudo-spectral method to calculate the nonlinear term.The velocity, the vorticity, and the curl of vor- ticity are expanded as

whereBkare helical waves in a bounded spherical domainD, defined as the eigenfunctions of the curl operator with the no- penetration boundary condition

{λk} are the eigenvalues of the curl operator, which can be consid- ered similar as ‘wavenumbers’ in Fourier space.Yoshida and Giga [32] have proved that {Bk} are complete for any solenoidal vector fields with the no-penetration condition and satisfy

where the asterisk denotes complex conjugate and the subindexkofBkis an abbreviation ofk=(q,l,m)[33,34] .Here,landmare indices of the spherical harmonics.The eigenvalueλk=λq,lis independent ofmandλ−q,l= −λq,l.ABandAkare the auxiliary fields to satisfy the no-slip boundary condition, whereABis determined by the prescribed velocity on the boundaryuBandAkis determined by the helical waveBk(see Ref.[30] for details).We substitute Eqs.(4) - (6) into the Navier-Stokes equations Eqs.(1) and (2) in consideration of ∇2u= −∇ ×ω, take inner products with the individualB*k, and integrate each term in the whole do- mainD.Equations (1) and (2) are thereby converted into a set of ordinary differential equations forak

body forcef,AB, andAi.Note thatBas a subscript indicates ‘boundary’.Since Eq.(3) shows thatuB= 0 , we haveAB= 0 anddk=bk= 0 in the problem considered here.

The infinite set of ordinary differential equations is truncated for |q| = 1,2,...,Nmax ;l= 1,2,...,Lmax ; |m| = 0,1,2,...,l.Sinceλkonly depends onqandl, the primitive HWD energy spectrum is defined as

whereVis the volume of the sphere, and the corresponding coarse-grain-averaged spectrum is

To investigate the effects of different rotation on flow structures and nonlinear inertial waves in a fluid sphere, we conducted a se- ries of direct numerical simulations (DNS) with different system rotations and a fixed sphere radiusro.All present DNS adoptedNmax ×Lmax = 240 ×84 with a maximum wavenumberλmax≈756 in helical-wave space, corresponding to a resolution ofNr×Nθ×Nφ= 960 ×256 ×256 in physical space.Here,Nris the number of Gauss-Legendre quadrature points in the radial direction.NθandNφare numbers of mesh points uniformly distributed in theθandφdirections, respectively.Note that our results do not change when a finer gridNmax ×Lmax = 240 ×169 (corresponding toNr×Nθ×Nφ= 960 ×512 ×512) is used.To achieve a station- ary flow state, a constant forcing functionwas adopted [24,35] , which satisfys

Becausefis real, the coefficients satisfy the conditions.Moreover,fisnon-helical, andzero ontheboundary, sincefq,l,m= −f−q,l,m.Table 1 displays a summary of parameters for our DNS, whereΩrepresents the system rotation rate.Statisti- cal quantities are obtained from the time average of the stationary states, including the total energyE, the mean energy dissipation 〈ε〉 , the integral scaleL, the Taylor microscaleλT, the Kolmogorov scaleη, Reynolds numbers based onroandλT, and the large eddy turnover timeτ0.Some of their definitions are shown below which are analogous to those in Fourier space.δis the average boundary layer thickness which will be discussed later.

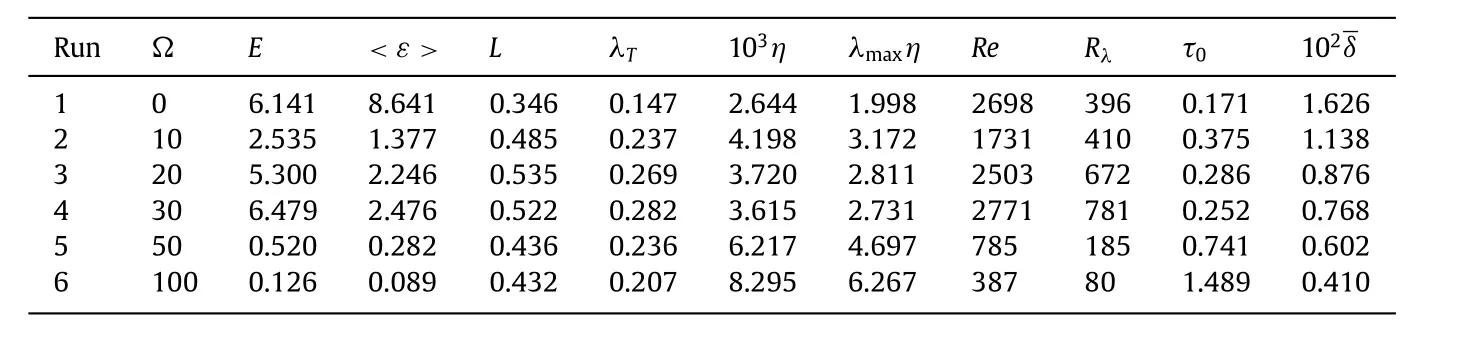
Table 1 Summary of parameters for the DNS of turbulence in a rotating sphere.For all cases, the forcing wavenumber λf = λ2 , 2 , the forcing magnitude f 0 = 1 . 173 and the viscosity ν= 7 . 5 ×10 −4 .

Figure 1 a shows that the kinetic energyE(t)reaches a sta- tistically steady state for all the simulations.For Run1-Run3,Efluctuatesirregularly withtime, indicating apossibleturbu- lent state.At later times,Eis quasi-periodically oscillatory for Run4, while reaches small constant values for Run5 and Run6.Figure 1 b presents the normalized HWD energy spectra of the steady states for all cases.For Run1 whereΩ= 0 , there exists a helical wavenumber range with −5/3 scaling, consistent with the results of Ref.[35] .When system rotation is introduced, a scaling in the ‘inertial range’ with slope sharper than −5/3 and shallower than −3 is observed for Run2-Run4.However, there does not ex- ist such an “inertial”helical wavenumber range for Run5 and Run6 with larger system rotation.Note that a clean −5/3 Fourier spec- trum is developed for the case in a periodic box with system rota- tion [36] .

Next we investigate the flow structures and the associated in- ertial waves.The classicalQ-criterion is used to identify the vor- tex structures, which are further divided into cyclonic and an- ticyclonic vortices according to the sign of their vertical vortic- ity.TheQ-criterion identifies vortices as connected fluid regions in whichlarger than some threshold value, whereis the symmetric rate-of-strain tensor and−(∇u)T] is the antisymmetric vorticity tensor.Re- gions withQ>0 andQ<0 are called vortex-dominated and strain-dominated, respectively.

Figure 2 displays instantaneous plots of isosurfaces ofQand contours of vorticity in the equatorial plane and in a meridional plane for Run1, Run2, Run4 and Run5.Note that isosurfaces ofQare color-coded with the sign of vertical vorticityωzin Fig.2 c and 2 d, wherein reddish color representsωz>0 and bluish color rep- resentsωz<0 .Results of Run3 and Run6 are similar with those of Run4 and Run5, respectively.For Run1 with a zero system rotation, the intense vortex structures are tube-like (Fig.2 a), which are sim- ilar as those observed in homogeneous isotropic turbulence [37] .Compared with Run1, Fig.2 b shows that in Run2, small-scale struc- tures are reduced and vortex tubes have a preferential alignment to the axis of rotation, which indicates the existence of an inverse energy cascade and two-dimensionalization of the flow field.For Run3 and Run4 with larger system rotations, the flows are dom- inated by a large-scale anticyclonic vortex structure near the ro- tation axis of the sphere (Fig.2 c), which is shown to be a mani- festation of the domination of geostrophic modes later (see Fig.3 c and 3 d).As the system rotation further increases (Run5), the dom- inant flow structures turn into a cyclonic and an anticyclonic vor- tex, which emerge from the upper and lower boundaries, respec- tively, as shown in Fig.2 d.The intensity of the anticyclonic vortex is stronger than that of the cyclonic one, as indicated by the con- tours of vorticity in the meridional plane.

To further investigate the above variation of flow structures un- der different rotation rates, we decomposed the flow field into dif- ferent components of inertial waves.Zhang et al.[26] first uncov- ered the explicit general analytical expressions of inertial waves in a rotating fluid sphere, which are discussed in detail in Ref.[27] .Here we only present a brief introduction of inertial waves in rotating spheres.EmployingΩ−1as the time scale,roas the length scale, a characteristic speed of the flowUas the veloc- ity scale, andUΩroas the unit of the modified pressure, linear non-dimensional inviscid equations of the fluid system are derived

from Eqs.(1) and (2) :

and the no-slip boundary condition Eq.(3) is then relaxed to the inviscid boundary condition

Inertial waves are solutions to Eqs.(15) - (17) in the form

whereris the position vector andσ(0 ≤|σ|<1) represents the half-frequency of oscillatory motions.

In a rotating sphere, the geostrophic modes (GMs),G2k−1(r,θ), are the solutions corresponding toσ= 0 , wherek= 1,2,3,....The solutions withσ/ = 0 are divided into four classes with dif- ferent spatial symmetries: (i) equatorially symmetric inertial os- cillation (ESIO); (ii) equatorially symmetric inertial wave (ESIW); (iii) equatorially antisymmetric inertial oscillation (EAIO) and (iv) equatorially antisymmetric inertial wave (EAIW).Here inertial os- cillations refer to oscillatory motions that are axisymmetric with respect to the rotation axis, and inertial waves refer to oscillatory motions that are non-axisymmetric with respect to the rotation axis and progradely or retrogradely propagate in the azimuthal di- rection.We employto represent ESIO and ESIW, andto represent EAIO and EAIW.In the cylindrical co- ordinate where the axial direction is along the rotation axis,mis the azimuthal wavenumber,nis representive of the degree of the axial complexity andkreflects the radial structure.Note that |σmnk| increases withkfor the samemandn.For ESIO,m= 0 ,

k= 2,3,...,andn= 1,2,...,(k−1); For ESIW,m= 1,2,...,k= 1,2,...,andn= 1,2,...,(2k); For EAIO,m= 0 ,k= 1,2,...,andn= 1,2,...,k; For ESIW,m= 1,2,...,k= 0,1,2,...,andn= 1,2,...,(2k+ 1).G2k−1 ,uESmnk,uES,*mnk,uEAmnkanduEA,*mnkconstitute an orthogonal and complete system of incompressible velocity fields in a rotating fluid sphere [38] .Therefore, a complicated flow fielduin a rotating sphere can be expanded as

where the inertial modes are normalized and the expansion coef- ficients can be obtained as following

Because the velocity field is real, the coefficients of(orare the conjugate of those of.The kinetic energyE(t)at timetcan be expressed as

In order to better visualize the distribution of energy in different modes, we define the inertial-mode spectrum as

whereIrepresents the index of an inertial mode.Note that we consider one pair ofas oneIhere.

Figure 3 displays the time-averaged inertial-mode spectrumEM,avefrom thestatistically steady states of all simulations.Note thatIis arranged in the following order: GM, ESIO, ESIW, EAIO and EAIW, whereink,n,mincreases in sequence.The inertial-mode space is truncated withkmax = 6 for GM andmmax =nmax = 6 for others.For Run1, six modes with substantial portions of energy are marked, including two ESIWs, one EAIO and three EAIWs (Fig.3 a).They are all with smallmandn, which should be caused by the large-scale external forcing.Besides, other modes hold significant energy, indicating that the turbulent flow has a broad spectrum on inertial modes.Actually, the total energy of all the modes consid- ered in the spectrum isEK,trunc ≈0.6935EK.Figure 3 b shows that the energy in GMs is excited and that in EA modes is suppressed in Run2, compared with Run1 with no system rotation.Except three GMs, all the dominant modes are QG modes withk= 1 , including six ESIWs and one EAIW.The total energy of all the modes consid- ered in the spectrum isEK,trunc ≈0.9405EK, indicating that these modes are enough to describe the primary structures in the flow.For Run3 and Run4 with larger system rotation, Fig.3 c and 3 d dis- play dominations of several GMs.All other dominant modes are QG ESIWs and the energy in EA modes is further suppressed com- pared with Run2.The period of the quasi-periodic oscillation ofEK,T≈3.6 s in Run4, is two orders of magnitude smaller than those of two dominant ESIWs.Therefore, the quasi-periodic oscillation ofEKis resulted from nonlinear interactions of different modes, which is discussed in detail in later.The total energy of all the modes considered in the spectrum isEK,trunc ≈0.9492EKin Run3 andEK,trunc ≈0.9693EKin Run4.Figures 3 e and 3 f show that both the two dominant modes are QG ESIWs in Run5 and Run6.Energy fluctuations are negligible for all inertial modes (not shown), indi- cating that the flow states are laminar.The total energy of all the modes considered in the spectrum isEK,trunc ≈0.9962EKin Run5 andEK,trunc ≈1.0 0 0 0EKin Run6.

Inertial-mode decomposition can also be considered as a time- scale decomposition of the flow field.The energy spectrum of the magnitude of inertial-mode half-frequencies |σ| is defined as

which is shown in Fig.4 for all cases.Note that only the iner- tial modes considered in Fig.3 are adopted when we calculate Eq.(25) .Figure 4 shows thatE(|σ|)is flat for nearly all |σ| in Run1, indicating that the energy is evenly distributed on inertial modes with different |σ| .As the system rotation increases, en- ergy tends to concentrate on inertial modes with small |σ| and develops a |σ| -range with −5/3 scaling in Run2, Run3 and Run4.For Run5 and Run6 with larger system rotation, inertial modes with small |σ| hold more energy and there is a range satisfyingE∝ |σ|−3.Figure 4 also quantitatively demonstrates whether the QG assumpution is applicable for cases with system rotation.For turbulent states in Run2, Run3 and Run4, inertial modes with large |σ| still hold an important portion of energy, which invalidates the QG assumption.However, the situation is opposite in Run5 and Run6.

The spherical confinement changes the eigenfunctions of the curl operator from the Fourier basis in the periodic case to the helical-wave basis, of which the nonlinear interscale interaction is not Fourier-triadic [35] .Therefore, it is worth to study the nonlin- ear energy transfer between helical waves under different system rotations.Multiplying Eq.(9) byc*kand adding the resulting equa- tion with its conjugate yields the energy equation in helical-wave spectral space

where the nonlinear energy transfer function

represents the energy transferred to the helical wave indexed bykper unit time through nonlinear interactions among helical waves in a sphere;

is the energy transfer function induced by Coriolis force;

indicates the viscous dissipation in the helical wave indexed byk; the boundary effect term

represents the work conducted by the wall friction per unit time, sinceis the helical-wave coefficient of the wall frictionτ=νn×ω; denotes the external energy input rate in the helical wave indexed byk.

Figure 5 showsTnl,Trot,DandWbobtained from the station- ary states of Run1, Run2, Run4 and Run5, respectively.We focus on the wavenumber range away from the forcing scale.Figure 5 a shows thatTnl(λ)>0 when 0.1<λη<1 in Run1, which indicates that the corresponding helical waves gain energy from the non- linear transfer.For Run2 shown in Fig.5 b,Tnl(λ)is still positive away from the very large forcing scale.However, the magnitude ofTnl(λ)is smaller compared with Run1.For Run4 with larger system rotation than Run2, Fig.5 c displays thatTnl(λ)has small negative values when 0.1<λη<1 , which corresponds to the existence of an inverse energy cascade (see later discussion).For Run5, Fig.5 d shows thatTnl(λ)is close to zero at all scales, indicating that the nonlinear energy transfer is negligible.This is consistent with that the flow state is laminar in Run5.Except in Run1 whereΩ= 0 ,Trot(λ)is positive away from the forcing scale, indicating that the corresponding helical waves gain energy from other helical waves by the rotation effect.This is different with the rotating turbulence in a periodic box, whereTrotis zero at all scales.As system rota- tion increases,D(λ)progressively concentrates on the forcing scale, which is consistent with the change ofE(λ)(see Eq.(29)).Wb(λ)is much smaller atλη≤1 for all cases.

To further illustrate the nonlinear energy transfer, we calculate the energy flux

as shown in Fig.6 .Π(λ)represents the energy transferred from helical waves withλk<λto those withλk>λthrough nonlinear interactions.As the system rotation increases, the forward cascade becomes weaker.When the rotation rate is larger than a critical value, e.g.for Run4, the inlet of Fig.6 displays that the energy cascade turns into dual cascades with an inverse cascade at large scales and a forward cascade at small scales [39] .Such a transition has been observed in different configurations [40] .The transition of the cascade is probably caused by the energy transfer function induced by Coriolis force,Trot, which acts as a source/sink of energy at different scales.This is also the reason whyΠ(λ)is nonzero at the smallestλ.Positions of the boundary layer thickness,y=δ, are indicated by circles.(b) The azimuthally averaged boundary layer thicknessas a function of colatitudesθfor all the simulations.

Next, In this section, we investigate the flow behavior near the no-slip boundary.The flow velocityucan be expressed as a sum of its radial componenturˆrand its tangential componentutin the form

Figure 7 a shows the magnitude of tangential velocityutas a func- tion of the distance from the boundary,y=ro−r, at the central meridianφ=πand different colatitudesθfor an instantaneous time in Run3.We found that although the profile ofutvaries withθ, each profile shows the existence of a viscous sublayer and a log law region, similar to the classical wall boundary pic- ture.Since the ‘free stream’ outside the boundary layer is compli- cated, it is difficult to compute the displacement thickness, mo- mentum thickness or energy thickness using the classical defini- tion.We define the boundary layer thicknessδas the position where d2ut/d(lny)2= 0 .Fig.7 b displays the distribution of the az- imuthally averaged boundary layer thicknessis indepen- dent ofθwhen the system rotaion is zero.When a weak system rotation exists,becomes larger nearthe equator andsmaller at high latitudes.For larger system rotation rates, two peaks ofemerge on both sides of the equator.The positions of the peaks move towards the poles as the system rotation rate becomes larger.Such ‘critical latitudes’ should be due to the Ekman pumping sin- gularities [41–45] .Table 1 shows that the average boundary layer thicknessδdecreases when the system rotation rate increases.

To further illustrate the flow behavior near the boundary, we also computed the wall friction.The wall friction imposed on the fluid sphere equals to the viscous stress on the spherical surfacer=ro:

whereμis the dynamic viscosity,SrθandSrφdenote components of the strain rate given by

and

respectively.The Hammer equal-area projection is adopted to dis- play the quantities on spherical surfaces, and it is given as follows

whereλh=φ−πis the longitude from the central meridian andφh=π/2 −θis the latitude.Two reference spherical surfaces are chosen for flow visualization atr1= 0.9937roandr2= 0.9039ro.

Figure 8 displays the wall frictionτwith its magnitudeτin Run1, Run2, Run4 and Run5.Note that in this section, Run3 and Run6 show similar results with Run2 and Run5, respectively.Com- pared with other cases,τare more turbulent on the spherical sur- face atr=r1 in Run1 (Fig.8 a), which is consistent with the flow structures shown in Fig.2 a, 2 b and 2 c.Figure 8 b shows that in Run2, areas with largeτlocate preferentially in the polar regions and midlatitudes, where large vorticity exists near the bound- ary (Fig.2 b).The preferential distribution of the areas with largeτshould be closely related to the interior large-scale structures (Fig.2 d).Figure 8 c displays that in Run4 areas with largeτlocate in circular regions at high latitudes, where the direction ofτis toward the poles.Different from Run4, areas with largeτconcen- trate on the polar regions in Run5, and the direction ofτis toward (or away from) the poles whenλh<0 (orλh>0).

To further study this change and its connection with interior flow structures, Fig.9 displays isosurfaces ofQ, and the three- dimensional perspective ofτanduron the spherical surface atr=r2 for Run4 and Run5.The streamlines ofuton the same spher- ical surface are also shown in Fig.9 c and 9 f.For both cases,uris of large magnitudes in the polar and high latitude regions (Fig.9 c and 9 f).Therefore, the mass flux between the boundary layer and the interior fluid mainly happens in these regions: the interior fluid is sucked into the viscous boundary layer whereur>0 and the fluid flows out of the boundary layer whereur<0 .Areas with largeutconcentrate on circular regions between the regions with large positiveurand those with large negativeur(not shown), indicating that the flow in the boundary layer is closely associated with the radial mass flux.It is found that in Run4 and Run5 the large pos- itiveurin the polar regions is induced by the Ekman pumping of the large-scale cyclonic and anticyclonic vortices (Fig.9 a and 9 d), consistent with results of the theoretical model [3,10] .

To show this quantitatively, we plot the conditional average 〈ur|Q〉 on the spherical surface atr=ro−δfor Run4 in Fig.10a .Compared with the strain region (Q<0),urhas larger positive values in the vortex region (Q>0), most of which hasωz<0 (Fig.9 a).Figure 10 b displays the conditional average 〈|ur||Q〉 on the spherical surface atr=ro−δfor Run5, indicating that the ra- dial flux is more intense in the vortex region than the strain region.The cyclone leads to negative values ofur, which indicate that fluid flows from the boundary layer into the interior, while the anticy- clone leads to an opposite effect.This is quantitatively shown by the averages ofurconditioned onQforωz>0 andωz<0 on the spherical surface atr=ro−δin Fig.10 c.

In the present study, we investigated the flow structures, non- linear inertial waves and energy transfer of the turbulence in a ro- tating sphere.Using a Galerkin spectral method based on HWD, direct numerical simulations under different system rotations are conducted, where a large-scale force is adopted as the energy generation mechanism.The classicalQ-criterion has been used to identify the flow structures, and the velocity field has been decom- posed into different inertial modes of a rotating fluid sphere.Note that results might be dependent on the particular way of forcing to some extent, and random forcing with fixed energy input will be used in our future work.The main results are summarized as follows.

The velocity fields in a non-rotating sphere (Run1) are similar with those for homogeneous isotropic turbulence, where the in- tense vortex structures are tube-like.The flow is forced in many inertial modes, where energy is transferred to other modes, result- ing in a broad inertial-mode spectrum.When the system is under small rotation (Run2), small-scale structures are suppressed and vortex tubes have a preferential alignment to the axis of rotation.Energy and fluctuations in certain GMs and ESIWs are significantly excited, while those in EA modes are suppressed.Note that the ex- ternal force is not equatorially symmetric.When the system rota- tion rate increases (Run3 and Run4), a large-scale anticyclonic vor- tex structure near the rotation axis of sphere dominates the flow, and it is dispalyed to be a manifestation of certain GMs.The en- ergy and energy fluctuations in EA modes are further suppressed.When the rotation rate further increases, as in Run5 and Run6, the dominant flow structures turn into a cyclone and an anticy- clone, emerging from the top and bottom of the boundary, respec- tively.There are only two QG ESIWs dominating the flow.Energy fluctuations are negligible for all modes, indicating that the flow states are laminar.In addition, the energy spectrum of the mag- nitude of inertial-mode half-frequencies |σ| is investigated.When there is no system rotation, energy is evenly distributed on inertial modes with different |σ| .As the system rotation increases, energy concentrates on inertial modes with small |σ| and develops a |σ| - range with −5/3 or −3 scaling.

The effect of spherical confinement on rotating turbulence has been studied through nonlinear energy transfer in helical-wave spectral space.When small system rotation exists, the forward nonlinear energy transfer gets weaker.As the system rotation be- comes larger than a critical value, dual energy cascades emerge, with an inverse cascade at large scales and a forward cascade at small scales.Different with the periodic case, Coriolis force results that energy transfers from large-scale to small-scale helical waves.

At last, the flow behavior near the no-slip boundary is stud- ied in detail.The average boundary layer thickness decreases as the system rotation rate increases.We found that the flow behav- ior near the boundary is closely related to the interior flow struc- tures, especially for the wall friction and the radial mass flux.The mass flux between the boundary layer and the interior fluid mainly takes place around the dominant vortices through Ekman pump- ing.A cyclone always induces inward flux while an anticyclone cre- ates outward flux.

Acknowledgements

We would like to acknowledge Zi-ju Liao and Wei-Dong Su for providing their HWD DNS code.T.L.thanks Zi-ju Liao for gener- ous computational assistance.This work has been supported by the National Natural Science Foundation of China (NSFC) Basic Sci- ence Center Program (No.11988102) and NSFC (No.91752201); Department of Science and Technology of Guangdong Province (No.2019B21203001); Shenzhen Science and Technology Inno- vation Commission (No.KQTD20180411143441009); Key Special Project for Introduced Talents Team of Southern Marine Sci- ence and Engineering Guangdong Laboratory (Guangzhou) (No.GML2019ZD0103).Numerical simulations have been supported by Center for Computational Science and Engineering of Southern University of Science and Technology.M.W.acknowledges the sup- port from Centers for Mechanical Engineering Research and Educa- tion at MIT and SUSTech.

Declaration of Competing Interest

The authors declare that they have no known competing finan- cial interests or personal relationships that could have appeared to influence the work reported in this paper.