Detection of mechanical stress in the steel structure of a bridge crane

Leopold Hrovský , , Dniel ˇCepic , Krel Frydrýšek

a VSB-Technical university of Ostrava, Faculty of mechanical Engineering, Institute of Transport, 17. listopadu 2172/15, 708 00, Ostrava - Poruba, Czech Republic

b VSB-Technical university of Ostrava, Faculty of Mechanical Engineering, Department of Applied Mechanics, Ostrava - Poruba, Czech Republic

Keywords: Crane skewing Mechanical stress detector Mechanical stress FEM Overhead crane

ABSTRACT A significant negative aspect in the operation of bridge-type cranes are the technical problems associated with wear of the wheels and the crane track, which causes crane skewing.The main causes of crane skewing include unevenness of the crane track, unequal loading of the traction drives depending on the position of the crane trolley, slips and different sizes of travel wheels and combinations of these causes.Firstly, this paper presents a design solution that can be used to detect the magnitude of mechanical stress and deformation of the steel structure of the crane, caused by the effects of skewing.The me- chanical stress generated by the transverse forces of the deformed geometric shape of the crane bridge structure is recorded by mechanical stress detectors installed in the inner corners of the crane bridge.The resulting electrical signal from element mechanical voltage detectors, loaded by axial forces, can be used for feedback control of separate crane travel drives controlled by frequency converters.Secondly, this paper presents the calculation of the lateral transverse forces according to CSN 27 0103 and the de- termination of the values of mechanical stresses of the deformed steel structure of the crane bridge of a two-girder bridge crane using the finite element method in the program MSC.MARC 2019.Finally, this paper presents the structural and strength design of mechanical stress detectors and the conclusions of laboratory tests of axial force loading of mechanical stress detectors on the test equipment.At the same time, it presents records of the measured axial forces acting in the mechanical stress detectors, arising from the deformation and warping of the crane bridge by the known magnitude of the axial force acting on the crossbeam and from the deformation of the crane bridge caused by the crane operating modes.

Elimination of crane skewing on crane tracks is currently based on several principles, of which the best known and most widely applied in practice are the optical methods [1] , ultrasonic [2] and strain gauges [ 3 , 4 ].The “Geotronics”[5] optical method is based on the principle of evaluating the speed of movement of laser beams.Laser transmitters are placed on both end faces of the crossbeams in the direction of travel of the crane, and reflector elements of the laser beams are located at the end points of the crane tracks.During continuous measuring of the distance of the laser transmitters from the reflectors, signals are sent to the drive to control the speed of the driving electric motors.The principle of “Electronic flanges”[2] uses four ultrasonic sensors, which con- tinuously measure the lateral distance of the corner parts of the crane bridge from the railhead.The control circuit (programmable logic controller) evaluates four sensor signals.The output signal from the controller enables independent control (by changing the travel speeds of the right and left side of the crane controlled by frequency converters) of the circumferential speeds of the driving crane wheels.

The principles [ 1 , 2 ] are based on the assumption that travel wheels with double-sided flanges mounted on opposite cross- beams (driven by separate drives) run parallel, and thus travel the same path in the same moment of time.This principle is also used by mechanisms with a fixed or electric shaft, which can achieve the same speed of the drive motors, but due to different gears it is not possible to ensure uniform wear of the wheels, resulting in increased stress on the steel structure of the crane from the even travel of opposing sides (crossbeams) of the truck.

In industrial practice, it is possible to eliminate or completely negate the effects of crane skewing on bridge-type cranes by a method that is based on the control of traction motors [5] with regard to minimizing the mechanical stress of the crane structure [ 3 , 4 ].In this method, information on deformation and mechanical stress is obtained from strain gauge bridge sensors [ 6 , 7 ] located at a suitable place on the crane bridge structure.The magnitude of the deformation of the steel structure of the crane bridge often does not reach such optimal magnitudes that would make it suit- ably detectable by foil strain gauges attached to selected places of the crane bridge [4] .

More suitable solution for gaining knowledge on the magnitude of mechanical stress in the deformed structure of a crane bridge is to install so-called mechanical stress detectors (hereinafter MSD) in pre-selected places on the crane bridge [8] .The MSDs are usually mechanically attached in places of the steel structure of the crane bridge [9] , where the ends of the main girders are connected to the crossbeams, see Fig.1 .

The effects of transverse loads, which according to CSN EN 13001-2 + A3 [10] are included in the category of intermittent loads, when the crane travels along a crane track formed by steel rails, were detected on a double girder bridge crane 2 ×6.3 t-31.5 m, see Fig.1 .

The main girder of the crane and its static cross-sectional values are shown in Fig.2 .

The cross beam of the crane and its static cross-section values are shown in Fig.3 .

According to CSN 27 0103 [11] , the horizontal lateral forcesHtpv, from the crane skewing on the crane track can be determined ac- cording to relation (5).The crane skewing factorλin Eq.(1) as- sumes the following limit values: 0.05 ≤λ≤0.2.K1 (Eq.(3))K2(Eq.(2)), the wheel load on the more (less) loaded branch of the crane track from the net weight of the cranemc(see Table 1) and the blockmkwith a total loadmq is in the most efficient position (Fig.4).

Table 1 Base parameters of a two-girder bridge crane.

The final value of axial forcePyc = 8 kN is selected by rounding.

Calculation of applied mechanical stresses and axial forces in the measuring element MSDs and deformation of the steel struc- ture of crane bridge of double girder bridge crane 2 ×6.3 t-31.5 m (Fig.1) was performed by finite element method (FEM) in the MSC.MARC 2019 program.During the calculation, the geometric model of the crane was transformed into a shell (this is suitable for thin-walled structures, which the box-type beams (Fig.2) and even crossbeams (Fig.3) of the 2 ×6.3 t-31.5 m crane can be con- sidered), which allows using fewer elements in the FEM calculation and thus greatly shortens the computation time.

A “relatively coarse”network was used to calculate the FEM, see Fig.5 a, formed by isoperimetric square shell elements with a max- imum size of 50 mm.An adaptive networking technique was used to refine the network, Fig.5 b.This is a process where, according to a certain criterion, the size of the elements is reduced locally to increase the accuracy.

At the maximum axial forcePyc Eq.(5) , the axial force of the maximum valueFmed(1) = -43.3 kN (see Table 2), which was determined by FEM, arises at the measuring element “1”(see Fig.6 c) MSD.The minimum value of the cross sectionSminof the measuring element MSD can be determined according to relation Eq.(7) .

In the FEM calculation, one of the girders (left girder on Fig.1) is assigned these boundary conditions (see Fig.6 a): at the place- ment location of the driven crane wheel, travel in the direction of crane travel (z-axis) and travel in they-axis are prevented (travel shiftsu,v,wsee Fig.6 a represent travel along the respectivex,y,zaxes).The force pairHtpv in Eq.(5) is introduced into the pins of crane wheels mounted on the opposite crossbeam (right in Fig.6 a).In the FEM computational model, the crane blocks are represented by material points connected with an assembly of MPC bonds.The blocks are fully loaded with the weight of the load, meaning that at both material points a force is exerted that is equivalent to the maximum load capacity of the blocksmq= 6.3 ×103kg.

During the calculation, 3 stress cases were considered, which were applied sequentially: gravitational force load, load by burden and load by a force pairHtpv in Eq.(5) .A continuous network was used for the calculation, and in places where it was not possi- ble to connect the elements by means of a network (places where gaps between the elements were created due to the use of shells), “glue”typecontacts are used.

The purpose of the FEM calculation in the MSC.MARC 2019 soft- ware environment was to determine the magnitude of the me- chanical stressσmed(i)in the MSD measuring elements (2, Fig.7), which are located in the corner parts of the crane bridge (Fig.1), meaning in places where the lower flanges of the main girders (Fig.2) are connected to the crossbeams (Fig.3).In the MSD mea- suring elements, the highest normal stressσmed(i)in the central surfaces of the shells was evaluated, meaning in the center parts of the cross-sectional thicknessSs of the MSD measuring elements.In Fig.6 c, the measuring MSD measuring elements are indicated by numbers 1 to 4 and the crane blocks are shown schematically.From the FEM results obtained, it is possible to calculate the re- sulting axial forces,Fmed(i) (see Table 2), acting in the measuring elements of the MSD.Figure 6 b shows the course of the largest normal voltageσmax(1)in the measuring element MSD “1”with a cross sectionSs Eq.(8) .

In the MSC.MARC 2019 software environment, the FEM deter- mined the mean value of the “median”stressσmed(i)and the nor- mal forcesFmed(i) (inducing the stressσmed(i)on the cross-sectional areaSs in Eq.(8) of the shell) in the individual MSD measuring el- ements, see Table 2 .

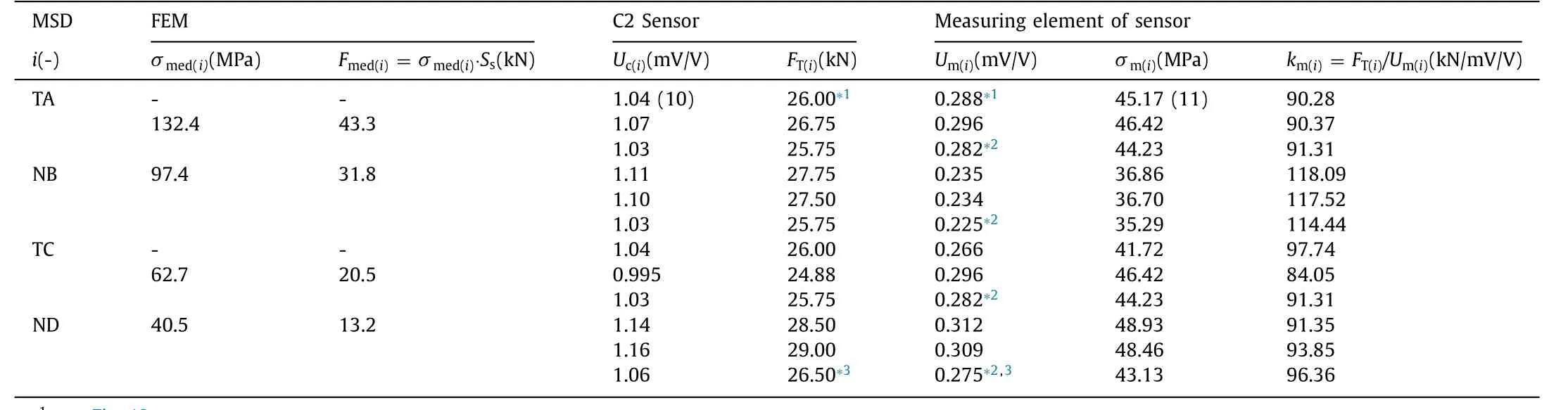
Table 2 Detected values of the relative U m of the MSD loaded by the force F T of the hydraulic jack.

The mechanical stress according to the HMH hypothesis was determined in all components of the crane bridge and was checked in the outer and inner layers of the shells.The stress in certain components (e.g.sidewalls) was affected by the occurrence of sin- gularities (places where there is an unrealistic increase in stress as the size of the element decreases).Singularities occur at sharp corners at the joints of sheet metal parts and are only of a local nature.Since the area of interest was to determine the stresses in the measuring elements of the MSD, the stresses in the other com- ponents were determined at sufficient distances from these singu- larities.The course of mechanical stress in the steel structure of the crane bridge is shown in Fig.8 a (on the side of detail A there are blocks which are not shown in Fig.8 a).The singularities in the sidewalls (see detail B) are shown in Fig.8 b, and the voltage out- side the singularity is shown in Fig.8 c.

The material 11523.1, from which the measuring element (2, Fig.7)φ30/22 mm MSD is made, acquires a yield strengthRe= 275 MPa.It is assumed that the measuring elements 2 (glued with foil strain gauges 1-XY11-6/350 [12, pp.28/96]) will be loaded to a maximum of 50% of the yield strengthRe , meaningRev = 0.5Re = 137.5 MPa.

The main part of the MSD is the so-called measuring element (2, Fig.7) whose cross sectionSs(8) and construction dimensions are designed so that it senses the mechanical stressσmacting on it over the whole range of its limit values.Measuring element 2 MSD, see Fig.7 , with an actual cross sectionSs (8), is designed as a tube with an outer diameterD= 30 mm and an inner diameterd= 22 mm.

With the force pairHtpv(5) acting on the steel structure of the crane bridge 2 ×6.3 t-31.5 m (Fig.6 a), a mechanical stress,σmax= 132.4 MPa, is generated in the cross sectionSs (8) of the MSD measuring element (see Fig.6 b).The maximum axial forceFby which the MSD measuring element (2 , Fig.7) installed on the bridge crane 2 ×6.3 t-31.5 m can be loaded, can be determined according to relation Eq.(9) .Figure 6 c shows the deformation of the crane bridge structure and the mean amount of movement of the crossbeamDz= 29.8 mm, when the force pairHtpv (5) acts on the crane bridge 2 ×6.3 t-31.5 m according to CSN 27 0103 [11] .

For the purposes of MSD calibration, the Yokogawa DL750 [13] measuring apparatus was used, in which relation (11) [7, p.13] is used for the calculation of the measured stress valueσmof the deformed cross sectionSs of the MSD measuring element covered with resistance film stress gauges (1-XY11-6/350 [12]).

Assuming that at the maximum possible load of the tensile force transducer 5 ×103kg ～= 50 kN it is possible to read the voltage valueU= 1 V at 10 0 0 times gain at the supply voltageUN= 5 V of the pressure force transducer C2 [14] , then the voltageUc= 1.04 mV/V corresponds to the tensile forceFin Eq.(10) , see Table 2 .

To verify the functional properties of the MSD (F ig.7) on the test equipment (F ig.9) , the MSD 1 were subjected to a tensile forceFT exerted by the compressive force of the hydraulic jack 4, the in- stantaneous value of which was detected by the tensile force sen- sor C2 3. On the display of the Yokogawa DL750 [13] measuring apparatus, it was possible to read the instantaneous value of the compressive forceFTderived by the hydraulic jack 4, which man- ifests itself as a tensile force on the MSD measuring element 1. At the same time, the time course of the proportional extensionUm of the MSD measuring element is shown on the display of the measuring apparatus [13] , see Table 2 .

wherent= 2.6 for the total number of strain gauges used 4 (of which 2 strain gauges are glued longitudinally and measure longi- tudinal elongation and 2 strain gauges are glued transversely and measure transverse contraction,nt= 2 + 2μ= 2.6, proμ= 0.3).

On the display of the Yokogawa DL750 measuring apparatus, it was possible to read the instantaneous value of the compres- sive forceFT (F ig.10) derived by the hydraulic jack 4 (see Fig.7) which manifests itself as a tensile force on the MSD measuring element 1.

The 2 ×6.3 t-31.5 m bridge crane (Fig.1) without load (i.e.without suspended load of massmq on the hook of both crane blocks), with crane blocks located in the middle of the span of the crane bridge, was moved several times manually and backwards and forward, with released travel brakes, in the direction of the crane track in order to release the internal stress in the steel struc- ture of the crane in the horizontal direction.

After the crane movement was completed, it was checked whether all wheel flanges of the wheels are equally spaced from the sides of the railheads (wheel diameterDk= 320 mm, distance between wheelsa= 75 mm, rail widthb= 55 mm).After ver- ifying the identical distance of the flanges from the sides of the railheads, four MSDs (Fig.7) (which were marked TA, NB, TC and ND) were welded in the inner corners of the crane bridge, see Fig.15 .

The solder pads of each 1-XY11-6/350 strain gauge [12] (glued to the measuring section, see 2 Fig.7 , MSD) were conductively connected with a 3-core cable to the corresponding connectors of the 9-pin D-SUB socket.Each of the four MSDs was connected via its own electrical cable (terminated with a 9-pin D-SUB plug) to a Yokogawa 750 [14] measuring apparatus.

A bracketP(Fig.11) was welded to the vertical steel girder at the end of the crane track so that the longitudinal axis of the hub 8 was concentric with the axis of the bumper attached to the front face of the crossbeam (Fig.3) of the crane bridge.A hydraulic jack 4 [15], hubs 5 and 6, mechanically connected using screws, and a strain gauge load cell 3 [15] were placed on the bracket (seeP, Fig.11) , to which a hub 8 was attached by screws, the front surface of which rested on the spring bumper of the crane (F ig.11) (which was secured against compression).

The travel wheels of the crane bridge placed in the second crossbeam (on the opposite side of the crane bridge) were secured with a stop (mechanically attached to the crane rail) against over- running (i.e., shifting in the direction of the crane travel).After locking the travel wheels of the opposite crossbeam and complet- ing the installation of the bracket (P, Fig.11) , a horizontal forcePyc= 8 kN in Eq.(6) was exerted by the hydraulic jack 4 onto the front surface of the crossbeam, in the direction of crane travel.

The horizontal forcePyc and the values of the relativeUm(i)of the DMS component measuring elements were detected by the strain gauge C2, see Fig.12 a, and these signals were recorded by a Yokogawa 750 [13] measuring apparatus.Figure 12 b and Table 3 present the values of the axial forcesFm(i) , which can be calcu- lated according to relationship Eq.(12) if the values of the relativeUm(i) (mV/V) of the respective MSD are known (they are read by the measuring apparatus Yokogawa 750).

After connecting all eight strain gauges T1 (T5), T2 (T6), T3 (T7) and T4 (T8), see Fig.15 , placed on the SMD, into the Wheatstone resistor bridge and supplying the electrical signalUmc(mV/V) in Eq.(13) , which is given by the “sum of signals (TA - NB + TC - ND)/2”(see Table 3) from the MSD, graphic records were obtained into the measuring apparatus Yokogawa 750 [13] , see Fig.13 .

Table 3 Detected values of a relative U m(i) of the MSD during skewing of the crane bridge by axial force P yc .

After removing the stop, which prevented the travel (in the di- rection of travel of the crane) of the travel wheels placed in the second crossbar, i.e.after releasing the crane on the previously braked side and removing the bracketP(F ig.11), the 2 ×6.3 t- 31.5 m crane was ready for operational measurements.

Operational measurements recorded the generated forces, which are manifested during the working cycle of a two-girder bridge crane.The effects of crane bridge deformation were de- tected for: 1) travel of unloaded (Fig.14) and loaded crane with blocks in the middle of the bridge, 2) travel of unloaded and loaded crane with blocks moved to the extreme edge of the bridge, 3) suspension and lifting of loads with blocks in the center, as well as moved to the edge of the bridge and 4) lowering the load with blocks in the middle, and moved to the edge, of the bridge.

The 2 ×6.3 t-31.5 m bridge crane (Fig.1) without load, with crane blocks located in the middle of the crane bridge span, was driven along the length of the crane track and the induced inter- nal stress in the steel structure of the crane bridge was detected by installed MSDs.Instantaneous values of axial forces, see Fig.14 , acting on the individual measuring elements of the MSD from the effects of the crane skewing were recorded by the Yokogawa 750 [13] measuring apparatus.

All eight strain gauges T1 (T5), T2 (T6), T3 (T7) and T4 (T8) are connected to a Wheatstone resistance bridge, see Fig.15 .The out- put signal from the measuring bridge is fed via a single-channel measuring amplifier (Industrial Amplifier) from Hottinger Baldwin Messtechnik GmbH under the trade name CLIP AE301 [16] to the Yokogawa 750 [13] measuring apparatus.

A record of the entire range of experimental measurements per- formed of the relative deformations of partial MSDs caused by the crane travel and the suspension of the load is presented (see Fig.6 a).The sum signalUmcof the relative deformations of the four MSDs is presented in Fig.6 b.

The highest value of proportional deformation in the MSD mea- sured in the record shown in Fig.16 a corresponds to 0.12 mV/V, which, in comparison with the voltageUm= 0.312 mV/V (see Table 2), which corresponds to the standard CSN 270103, wherePyc = 8 kN andHtp = 47 kN, corresponds to 38% of the calculated transverse force (Htpv = 47 kN in Eq.(5) or Fig.6 a) according to the CSN 270103 standard.

The sum signalUmcof the relative deformations of the four MSDs, see Fig.16 b, can be used for feedback control of separate crane travel drives controlled by frequency converters.

The aim of the operational measurements performed on the 2 ×6.3 t-31.5 m crane was to obtain an electrical signal with prop- erties that will allow to control the frequency converters regulating the speed of the traction motors, which can eliminate the effects of crane skewing to a minimum.

To obtain the values of mechanical stress in the required places of deformation and known size (standard CSN 27 0103 recom- mended) force pairHtpv, steel structure of the crane, a 3D geo- metric model of the crane bridge was created.In the MSC.MARC 2019 program, the finite element method (FEM) was used to cal- culate the normal stress in the measuring elements of mechanical stress detectors (hereinafter only MSD), mechanically mounted in the inner corner parts of a two-girder crane bridge.

From the calculation of the maximum value of normal stressσmed(TA)= 132.4 MPa obtained in the measuring element MSD “TA”, the actual cross sectionSs= 3.27 cm2of all four measuring elements MSD was determined, which were glued with resistance foil strain gauges after their production.

In the laboratory, all four MSDs were gradually subjected to a tensile force ofFT～= 26 kN on a test rig, the magnitude of which was generated by a hydraulic jack and detected by a strain gauge load cell.With a known magnitude of the acting tensile forceFT, a constantkmwas determined for each MSD.If the measured elon- gation signal of the respective MSDUm(i) (mV/V), obtained from the measuring apparatus Yokogawa 750, is multiplied by the con- stantkm(i) , this result of the multiplication can be used to define the mechanical stressσm(i)acting in thei-th MSD measuring ele- ment.

The partial MSDs were connected to the inner corners of the crane bridge by welded joints and then two types of test trials were performed on a double girder bridge crane.

The purpose of the first test trial was to obtain the values of the actual mechanical stresses acting in the MSD measuring ele- ments with the exertion of the axial forcePycinto the front face of one of the crane crossbeams, provided that the other crossbeam is prevented from moving in the crane’s travel direction.The ax- ial forcePyc = 8 kN exerted by a hydraulic jack, when moving the front surface of the crossbeam in the direction of crane travel with the valueDz= 30 mm, excites the highest value of compressive forceFm(NB)= 20.16 kN in the measuring element MSD "NB" (see Table 3 and Fig.6), which corresponds to a stress ofσm(NB)= 61.65 MPa at the cross sectionSsof the MSD measuring element.The obtained maximum value of mechanical stress acting in the MSD measuring element from the experiment (σm(NB)= 61.65 MPa) is, compared with the value of stress determined by the calculation of FEM (σmed(TA)= 131.4 MPa, see Table 2), about 47%.

The detected values of the relativeUm(i)of the individual MSDs during the deformation of the crane bridge by the axial forcePycwere connected in the required order to the Wheatstone resistance bridge in the single-channel measuring amplifier CLIP AE301.The output sum signalUmc of the proportional deformations of the four MSDs can be used for the feedback control of the separate crane travel drives controlled by frequency converters.

The purpose of the second test was to obtain the values of the actual mechanical stresses that are generated in the measuring el- ements of the MSD during the warping of the crane bridge from the force effects that are manifested in the individual modes of the crane work cycle.

The maximum value of the relative of the MSD from the effect of crane bridge warping caused by crane travel and load suspen- sion was measured asUm(ND)=-0.12 mV/V (see Fig.16 a), which in comparison with the voltageUm = 0.312 mV/V (see Table 2) cor- responds to 38% of the calculated transverse forceHtpv .The sum signalUmc of the proportional deformations of the four MSDs (see Fig.16 b) can also be used for the feedback control of the separate crane travel drives controlled by frequency converters.

The solution described in this article is based on there being places on the supporting structure of the crane where the pro- portional deformations from transverse forces and from eccentric braking are the highest in terms of values.Therefore, at these sites, MSDs are placed, and fitted with strain gauge sensors of propor- tional deformations, where the highest proportional deformations are caused by transverse or eccentric braking.The individual strain gauges are connected to a special chain in the Wheatstone resis- tance bridge so that the measured values of proportional defor- mations from skewing or transverse or eccentric braking add up and other loads, especially symmetrical loads, to be canceled out, which the special strain gauge chain reliably performs.This pro- vides a distinctive electrical impulse signaling the start of skewing or eccentric braking, which serves as information for the feedback control of the separate drives of the crane trucks controlled by fre- quency converters.By slightly changing the speed of one side of the truck compared to the other side of the truck, which is de- termined by the signals from the strain gauge in terms of polarity and magnitude, the lateral and eccentric braking can be reduced to a minimum.

This work has been supported by The Ministry of Education, Youth and Sports of the Czech Republic from the Specific Research Project SP2021/53.

Declaration of Competing Interest

Manuscripts by name “Detection of Mechanical Stress in the Steel Structure of a Bridge Crane, was not been previously pub- lished in any language anywhere and that it is not under simulta- neous consideration or in press by another journal.