基于MATLAB回归分析在矿区通风粉尘排放预测中的研究

梁 敏

(天地科技股份有限公司，北京 100013)

可持续发展是当今国际社会的主题，它要求经济建设和社会发展要与自然承载能力相协调，发展的同时必须保护和改善地球生态环境，保证自然资源和环境成本以可持续的方式使用。

当前，我国发展过程中面临的突出矛盾之一就是环境污染问题，特别是空气污染问题尤为严重。一般而言，空气污染主要是由可悬浮颗粒物超标造成的，而粉尘的过量排放是造成可悬浮颗粒物超标的重要原因。煤矿通风排放物中的粉尘是一种重要的大气污染物，其主要成份是煤炭开采、掘进、运输过程中产生的岩粉和细微的煤炭颗粒，粉尘排出风井后会对空气产生污染，危及人类的健康，其在沉降后还会造成周围土壤的重金属污染[1]。

我国是矿物生产大国，众多矿山曾为社会经济发展提供了重要的物质基础，同时也造成了大量的环境问题[2]，摸清粉尘排放量及其分布对于粉尘防治具有重要意义[3]。目前，国内缺少对矿井通风粉尘的系统研究，因此，有必要在实地调研的基础上利用数值分析方法对矿井通风粉尘的排放情况进行分析，从而为通风粉尘的治理提供参考。

1 矿井粉尘排放情况调研

煤矿井下的主要尘源点是采、掘工作面，其产尘量占全矿井的85%以上[4]，井下粉尘经过风井后呈气流状排向大气, 逐渐弥散[5]，其排放量与矿井年产量、总回风量、粉尘浓度等数据密切相关。为了研究它们之间的关系，通过调研测试得到35座矿井的年产量、总回风量、粉尘浓度等数据，使用MATLAB软件对数据进行处理，建立数据间的函数关系，从而得到矿区煤矿粉尘排放量预测公式。

众所周知，预测公式能够使用的重要前提是要有相关变量的准确数据，即预测地区内煤矿的产量、总回风量、粉尘浓度等。一个矿区内的煤矿众多，由于矿井的总回风量和粉尘浓度数据需经现场测试收集，在计算矿区的通风粉尘排放量时，需对矿区内所有煤矿开展大规模调研测试，可见通过上述两个数据得到的预测公式在使用时很不方便，同时，矿区的煤炭总产量数据相比于矿井总回风量、粉尘浓度等数据更易获得。为了简化问题，使矿区通风粉尘排放量预测公式简便易用，仅就矿井年产量与粉尘排放量之间的关系开展研究。

为了研究矿井年产量和通风粉尘排放量间的规律，将调研得到的矿井年产量数据作横坐标，相应的通风粉尘排放量数据作为纵坐标。根据调研测试值，作出数据的散点图，如图1所示。

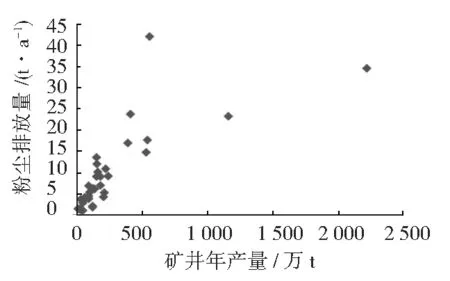
图1 矿井年产量与通风粉尘排放量数据散点图

由于散点图上的大部分数据在一定范围内呈现线性趋势，可以使用回归分析的方法进行数值分析。

2 数据拟合分析

数值分析运用十分广泛，它可以根据自变量的数值和变化，估计和预测应变量的相应数值和变化[6]。回归分析是一种常见的数值分析方法，属于定量分析的范畴[7]。它基于统计观测数据建立变量间的数学关系，通过分析数据间的内在规律，建立回归方程，可以确定两种或两种以上变量之间的相互依赖关系。按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析；按照涉及的自变量的多少，可分为一元回归分析和多元回归分析。在回归分析中，如果只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

2.1 模型建立

矿井年产量和粉尘排放量都是一维变量，而且散点图中的数据在一定范围内呈线性趋势，符合线性回归模型的构造条件，采用一元线性回归方法对数据进行拟合。

2.1.1 线性回归模型

一元线性回归的数学表达式为：

y=a+bx

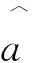
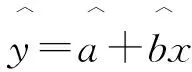
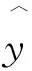
2.1.2 线性回归检验

在得到一元线性回归模型后，还需对其进行相关度检验，常用的检验方法有以下两种：

1)F检验。如果x和y有线性关系，则:

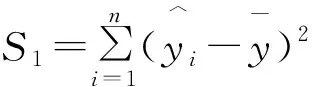
2)t检验。检验的原假设为：H0∶B1=0。对立假设为：H1∶B1≠0。如果原假设H0成立，表明因变量y与自变量x之间没有线性关系，即x的变化对y没有影响，一元线性回归不成立。如果当H1成立时，则认为自变量x对因变量y的影响显著，即回归模型成立。

2.1.3 拟合度分析

相关系数r用来表示自变量和因变量之间线性关系的密切程度，其计算公式为：

当相关系数r为正值时，表示自变量x和因变量y呈正相关；当r为负值时，自变量x和因变量y呈负相关。当r=0时，说明2个量之间无直线关系；当r=±1时，表示数据完全正相关或负相关，此时散点图上的数据都集中在回归直线上。通常认为当r的绝对值大于或等于0.75时，自变量和因变量具有很强的线性相关性。

2.2 回归分析

2.2.1 回归模型建立

套用一元线性回归方程建立粉尘排放量预测公式。

令x表示矿井年产量，y表示粉尘排放量，假定x和y有如下关系式：

y=a+bx

利用MATLAB中的regress函数对方程进行求解，对x和y作一元线性回归分析，从得到的结果看，常数项和回归系数的估计值分别为4.766 9和0.017 5，回归系数估计值的95%置信区间为[0.012 2，0.022 9]。

则线性回归方程可表达为：

y=4.766 9 + 0.017 5x

相关系数R的值为0.574 4，可见矿井年产量和粉尘排放量呈正相关，但由于R<0.75，表面两者间的线性关系不强。

2.2.2 残差分析

图2中的每条竖直线段都对应一组样本的残差和残差的置信区间，线段中点处的圆圈对应纵坐标为残差值的大小，线段上端点的纵坐标为置信上限，下端点的纵坐标为置信下限。若残差的置信区间不包括零点，则认为该组数据异常。

通过调用rcoplot函数，做出两组数据对应的残差和残差的置信区间图，数据对应残差如图2所示。通过对残差和残差的置信区间的分析，可以看出原始数据中存在的异常数据点。

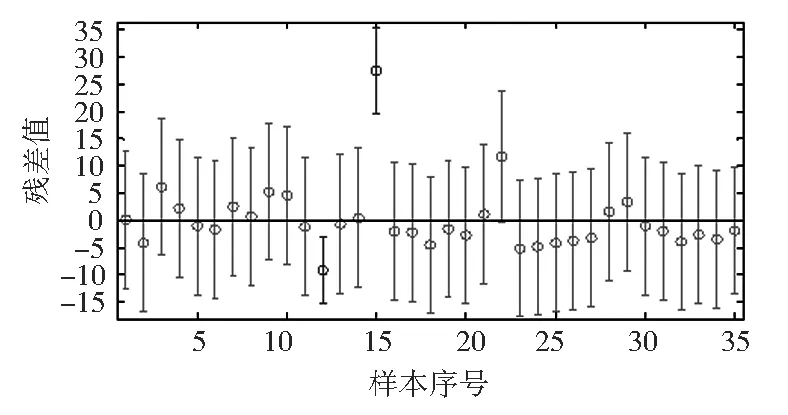
图2 残差图

从残差图可以看出：有两条线段与水平线(y=0)没有交点，可认为这两组数据为异常数据。

2.2.3 最优值求解

将异常数据剔除后重新对数据进行拟合，利用MATLAB对余下的数据作线性回归分析，从得到的结果看，常数项和回归系数的估计值分别为1.546 8和0.030 3，回归系数估计值的95%置信区间为[0.024 4，0.036 1]，数据散点与回归直线图见图3，则线性回归方程可表达为：

y=1.546 8+0.030 3x

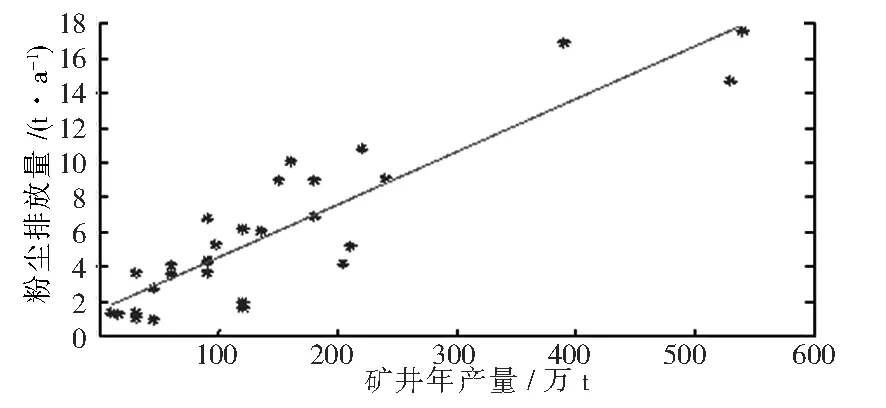
图3 数据散点与回归直线图

相关系数R的值为0.81，通过与上次回归分析的R值相比较，发现在剔除异常数据后，相关系数的值有了明显的提高，而且大于0.75，表明两者间具有很强的线性关系。

从数据散点与回归直线图可以看出，散点数据均匀分布在回归直线两侧，说明数据拟合度较高。

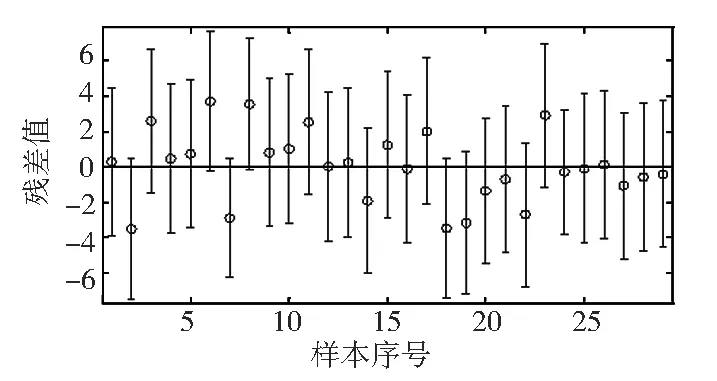
图4 残差图

从图4可以看出，样本中已没有异常数据，即样本与水平线y=0都存在交点。

3 结 语

1) 调研中绝大多数矿井的通风粉尘排放量与矿井的年产量呈现出一定的关联性。

2) 以矿井年产量和通风粉尘排放量数据为基础，建立了线性回归模型，分别采用MATLAB软件中的regress函数和rcoplot函数求解回归值，求解得到的线性回归方程相关性系数R=0.81，具有较高的可靠性，可用于估算样本矿区的通风粉尘排放量数据。

3) 数据分析中存在部分异常点，集中在年产量1 000万t以上的大型矿井，开采方式主要为综放开采，矿井产量与通风粉尘排放量之间的线性关系较弱，千万吨级矿井是未来矿井发展的主要方向，对于该类型矿井的通风粉尘排放情况有待进一步的研究分析。