Dense positrons and γ-rays generation by lasers interacting with convex target
2021-03-01NureliYASENBaisongXIE谢柏松andWeiyuanLIU刘维媛
Nureli YASEN, Baisong XIE (谢柏松),2 and Weiyuan LIU (刘维媛)
1 Key Laboratory of Beam Technology of the Ministry of Education, and College of Nuclear Science and Technology, Beijing Normal University, Beijing 100875, People’s Republic of China
2 Beijing Radiation Center, Beijing 100875, People’s Republic of China
3 Key Laboratory for Laser Plasmas (MOE), School of Physics and Astronomy, Shanghai Jiaotong University, Shanghai 200240, People’s Republic of China
4 IFSA Collaborative Innovation Center, Shanghai Jiaotong University, Shanghai 200240, People’s Republic of China
Abstract We use quantum electrodynamics particle-in-cell simulation to study the generation of dense electron-positron plasma and strong γ-ray bursts in counter-propagating laser beam interactions with two different solid targets, i.e.planar (type I) and convex (type II).We find that type II limits fast electron flow most effectively.while the photon density is increased by about an order of magnitude and energy by approx.10%-20% compared with those in type I target.γ-photon source with an ultrahigh peak brilliance of 2 × 1025 photons/s/mm2/mrad2/0.1%BW is generated by nonlinear Compton scattering process.Furthermore,use of type II target increases the positron density and energy by 3 times and 32%respectively,compared with those in type I target.In addition,the conversion efficiencies of total laser energy to γ-rays and positrons of type II are improved by 13.2% and 9.86% compared with type I.Such improvements in conversion efficiency and positron density are envisaged to have practical applications in experimental field.
Keywords: electron-positron pairs, γ-rays, particle-in-cell (PIC), nonlinear Compton scattering(NCS), multi-photon Breit-Wheeler proces, quantum electrodynamics, generation of dense electron-positron plasma
1.Introduction
Since the discovery of the positron in the 1930s, theoretical and experimental researches on positrons have been extensively performed [1, 2], among which the positron annihilation technology has been successfully applied to the study of material defects and phase transitions.Positron sources have often been the focus in basic and applied researches.Relativistic positron beams are important in experimental physics,and they can be directly applied to many scientific research fields such as nuclear physics [3], atomic and molecular physics [4], solid state physics [5], surface interface physics[6],material science[7],high energy physics[8]and medical imaging [9].Although the research on the generation of positrons by super-intense laser-solid target interaction has been greatly developed in recent years, the study of positron generation problems is still relatively limited.However,some physical problems concerning positron production and properties need to be carefully studied.In recent years, ultraintense (1019-1022W cm-2) ultra-short (tens of femtoseconds) laser pulse technology has made rapid progress [9].It provides not only the possibility of GeV electron acceleration by the nonlinear wake field [10]but also a new way to study tabletop relativistic positron beams.However,due to positron energy being low and its production small,current sources do not adequately meet the requirements of advanced research.

Figure 1.(a) The symmetrical planar target (type I) and (b) symmetrical convex target (type II) with two lasers each.The initial density is normalized to 1.1 × 1027 m-3.
In the coming years, laser pulses of 1023-1024W cm-2intensity may be realized by amplification technology, and some new ultra-relativistic plasma phenomena may occur[11-16].In such cases,the radiation reaction and the quantum electrodynamics (QED) effect need to be considered [13-20].The main nonlinear QED processes in the laser-plasma interaction at 10 PW intensity are the emission of synchronous photon rays by electrons in the laser’s electromagnetic field and e--e+pair production by multi-photon Breit-Wheeler processes,γh+nγl→ e-+ e+,where γland γhare,respectively,the laser and the high energy photons[21-23].Each reaction is a complete multi-photon process, the first of which being the nonlinear Compton scattering, e-+nγl→ e-+ γh[24-27],under the condition ofn≥ 2.
Development of laser-matter interactions and ensuing new phenomena, have resulted in more extensive research in this field, and the research on the laser-matter interaction is more and more extensive.The coupling between QED process and plasma dynamics in QED plasma produced by relativistic ultra-intense laser is a nonlinear and complex process, for example, the generation of ultra-intense γ-rays,and high energy dense electron-positron pairs [28-35].Numerical simulation is an important method describing such interactions.Therefore, we study the QED plasma phenomenon by using the simulation tools of the particle-in-cell(PIC)code EPOCH [30, 36-38] including such QED effects as the gamma ray emission of high energy synchrotron radiation and Breit-Wheeler pair production.In QED dominated regime,an electric fieldEshould be treated as strong field if it exceeds the Schwinger limit:1018V m-1.Such a strong field is potentially capable of providing, over an acceleration length of the Compton wavelengthan energy ξ to a chargewhich exceeds the electron rest mass energy ξ >mec2and thus separates virtual electron-positron pairs.
In our study, a two-dimensional simulation program is used to investigate the production of prolific γ-rays and dense electron-positron pairs.The main method is to hit two different types of solid aluminium targets by using two laser beams from the left and right boundaries at the same time with equal intensity.The production processes of γ-ray and electron-positron pairs are studied in detail.Moreover, the density, the energy spectrum, and the angular distribution in the two types of target are compared.It is found that the symmetrical convex target (target type II) can produce high energy, dense gamma rays and electron-positron pairs.Therefore,target II has obvious advantages over the first case in above aspects.The reasons for the higher photon and electron-positron pair productions are as follows: First, the type II target has a good binding effect that helps retain most of the hot electrons inside the target resulting in a larger collision interface in preparation for subsequent laser pulses.This, in turn, leads to increased gamma and e--e+pair production.Another reason is that the electric field generated under type II convex target has an inward focusing structure that has the effect of retaining the hot electrons.
2.Numerical simulations and results
2.1.Target configurations and simulation parameters
The two-dimensional numerical simulations are performed using the PIC code.The simulation box is 9λ × 8λ, divided into 800 × 900 cells with the grid sizeand each cell is filled with 500 electrons and 16 aluminium ions.The wavelength of the incident laser pulse is represented by λ = 1.0 μm.These two symmetrical targets are shown in figure 1.
Figure 1(a) shows a symmetrical flat target consisting of aluminium with a thickness of 1 λ and an electron density of 711nc[30,39],whereis the critical density for a laser wavelength of λ = 1.0 μm.According to the laser duration, the reasonable distance between the two targets is 2 λ.Figure 1(b) shows a symmetrical arc convex aluminium target with the same thickness of 1λ.In keeping with the 2λ spacing between the two targets, the inner and outer radii of the curved target,when just closed,are 6.76λ and 7.76λ.The two targets described above are composed of charge state 13 aluminium.

Figure 2.The logarithmic electron density distribution in type I(a)and type II(b).(c)and(d)the corresponding photon density distributions.Here, the electron and photon number densities are normalized by 1.1 × 1027 m-3.
This simulation uses twop-polarized laser pulses of equal intensity 4.0 × 1023W cm-2propagating from both sides of the simulation region with wavelength λ = 1.0 μm.The intensity profile is super-Gaussian in theydirection with a spot size of 1.0 μm.The laser has a duration of 46 fs with the rise and fall times of 2 fs each, and the laser amplitude keeps constant in the 42 fs.Furthermore, we use the absorption boundary inxdirection and the period boundary inydirection for both of fields and particles.
2.2.Simulation results
The density distributions of hot electrons for both types I and II are represented in figure 2.Careful observation of the figures indicates that the hot electrons produced in type II are primarily blocked in the convex region of the target where they form relatively dense concentration (figure 2(b)).However, this is not the case with the first type (see figure 2(a)).
For the corresponding photon density distributions, the production region of γ-photon is relatively large and its density is also larger in type II(figure 2(d)).However, the γphoton produced in the former type has small production region and low density (see figure 2(c)).
Similarly, an observation of the positron density distributions (figures 3(a) and (b)) with time at 46 fs indicates that those in type II have larger production area and higher density (figure 3(b)).However, the positrons produced in the type I have small production region and low density(figure 3(a)).This shows that the type II target is better than the type I in increasing positron production.In addition, we can also observe the distribution of positron energy flux from figures 3(c), (d).We find that the energy density distribution of positrons is similar to their number density.
In the figures 3(c), (d), the green and yellow dots represent low and high energy positrons, respectively.It is obvious that the number of high-energy positrons in type II is large, and the energy density is also high (figure 3(d)).
In contrast to type II,in type I the number of high-energy positrons is relatively small, and the energy is also lower(figure 3(c)).
For a quantitative comparison of the differences between the two targets, we show the slices of γ-photon and positron density at 4.5λ in figure 4.From figure 4(a), it is readily observed that the maximum density of γ-photons reaches 5.67 × 1030m-3under the type II.The density of γ-photons in type I is 7.41 × 1029m-3.Therefore, under the same conditions compared with type I, the density of γ-photons produced in the type II is increased by 7.7 times.Similarly,the maximum density of positrons reaches 7.63 × 1027m-3in type II (red line in figure 4(b)).

Figure 3.The logarithmic positron density distribution in type I (a) and type II (b).(c) and (d) the corresponding positron energy density distributions.Here, positron number density is normalized by 1.1 × 1027 m-3 and energy density converted to MeV.
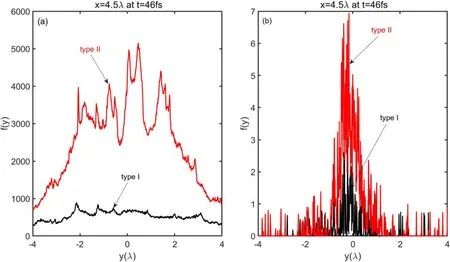
Figure 4.Slices of γ-photon and positron density at x = 4.5λ.Here, their densities are normalized by the 1.1 × 1027 m-3.

Figure 5.Longitudinal (a) and (b) and transverse (c) and (d) electric field distributions under type I and type II at time t = 46 fs.Here, the electric fields are normalized by 1 × 1015.
In contrast,type I results in a smaller positron density of 2.53 × 1027m-3.Therefore, compared with the type I case,the positron density under type II is enhanced by 3 times.This is primarily due, as stated previously, to the difference between the electric field distributions of the two cases(figure 5).
3.Analysis and discussion
Here we review and analyze the process that take place during the reaction of lasers with the symmetrical type I and II targets.Upon interaction of the opposite lasers with the type I target,the reflected wave will overlap with the incident wave,resulting in creation of standing waves on both sides of the focused target and formation of a potential well around it(figures 5(a)and(c)).This has an initial binding effect on the hot electrons in the interaction region.
In the type II case, upon the opposing lasers colliding with the target the standing wave initially, as in the type I case, occurs near thex-axis.However, with increasing distance along they-axis, although there are both incident and reflected waves present,the reflected laser intensity gradually decreases.This leaves the incident wave as the main contributor to the intensity on the contact surface.In addition,there is a confined electric field at the target wall(figures 5(b)and (d)) which, combined with the action of longitudinal electric field,results in enhanced QED effect in type II cases.
The distribution of energy spectra of γ-photons and positrons are shown in figure 6 for these two types of targets.The positron energy spectrum indicates a cut-off energy at 885.8 MeV with type II target (red line in figure 6).This is due to the standing wave occurring near the targetx-axis(figures 5(b) and (d)).With the change of vertical distance,the electric field intensity gradually changes and can accelerate and back off the electrons in the interaction region(figure 2(b)).
Furthermore, the confined electric field generated by the curved target inner wall has a strong focusing and blocking effect on the electrons in the interaction region.Thus, the combination of these effects results in enhancement of the QED reaction rate(figures 2(d)and 3(b)).The cut-off energy is also significantly 32.2% increased in the type II case compared to type I.In addition, as indicated in figure 6(inset), the cut-off energy of γ-photons in type II reaches 736.8 MeV, which is 12% higher than that of type I.
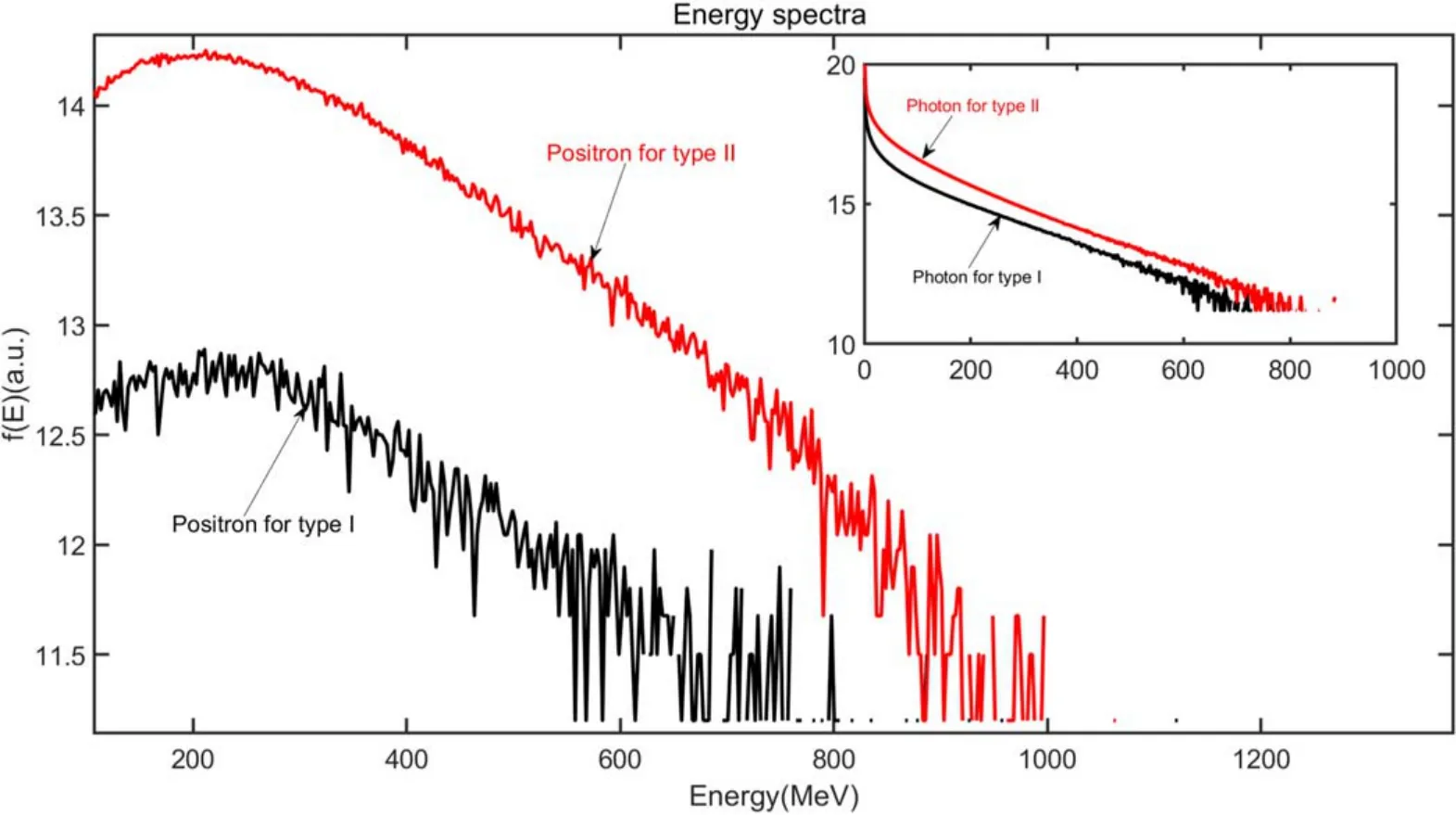
Figure 6.Energy spectra of γ-photons and positrons under type I (black line) and type II (red line).The energy spectra of γ-photons in the two targets are shown in the inset.Here, the energy spectra are plotted logarithmically.

Figure 7.The angular distribution of γ-photons and positrons at time 46 fs.Here the quantity is normalized by 1 × 1017.
In comparison,a full range of standing waves are generated at the type I target, the standing wave generated near the film can further form a potential well around the focused target(figures 5(a) and (c)), which has a binding effect on electrons.Over time, high power laser penetration of the target results in its deformation.The reflected wave shows focusing characteristics while the transmission wave shows defocusing characteristics causing deviation in the position of the strong laser field and, hence, plasma density.This, in turn, significantly reduces production of γ-photons and positrons (figures 2(c)and 3(a)).Therefore, the cut-off energies of γ-photons and positrons are reduced to 658.1 MeV (6 inset, black line) and 670.2 MeV (the black line in figure 6) respectively in type I.
Figure 7 may be used in a qualitative treatment of the γ-photon and positron beams in the two target type conditions.The angular distribution of γ-photons in type II has a higher peak at 0°.Its full width at half maximum(FWHM)is also larger than that of type I distribution.This is due to the higher production of γ-photons covering larger production area (figure 2(d)), hence resulting higher FWHM.
As can be seen from figure 7(b) there is a single peak in the angular distribution of positron at θ = 0° and FWHM of the positrons can be kept within 10° under type II.This is indicative of a large positron yield, small divergence angle and good restraining effect.In contrast, in type I the positron divergence angle is large and the yield is small.This is due to the deformation of type I in the tail of the interaction cycle when the position of the strong laser field begins to deviate from the plasma density, thus reducing the binding effect in the interaction zone by the reduced potential well generated by the standing waves on both sides of the target.In addition,the pressure effect of penetrating the laser field disperses the positrons, leading to larger divergence angle.The combined effect of the above processes increased positron production and smaller divergence angle in type II target case.Therefore,it can be said that good quality γ-photon and positron beams can be produced under type II.Such γ-photon and positron beams have potential applications in experimental physics and other applied fields.
According to the theory for generation of γ-photons and electron-positron pairs in QED, we initially analyse the generation process of high energy γ-photons under these two targets based on the theory of nonlinear Compton scattering[40, 41].We recall Compton scattering

where γland γhrepresent a laser photon and high-energy photon,respectively.From this process,the following may be deduced:existence of high density electrons in the interaction region, which increases the interaction probability with the laser photons propagating from both sides, and increases the increased the production of high density and high energy γphotons.Compared with the type I, the production of highdensity γ-photons produced under type II has increased by 7.7 times (see red line in figure 4(a)).In addition, the simulation results show that photon yields of 1.96 × 1014γ with an average energy at 4.46 MeV are generated under type II.Since the fast electrons transfer their energy to γ-photons during the nonlinear Compton scattering under type II, the average energy of the fast electrons in type II is 35.1 MeV.
However,1.82 × 1014γ-photons with an average energy of 4.12 MeV are generated under type I.In the case of type I,average energy of the γ-photons is smaller than that of type II.Because most of the fast electrons produced in this case are running out, only the fast electrons in the interaction region transfer their energy to γ-photons during the Compton scattering process.We recall that the calculation of the average energies of electrons, photons and positrons, by the program is based on the following expression

Here,niis the number density of particles,Δ =Vis threedimensional grid size,is the kinetic energy of particles,mec2is the rest energy of the electron andmeis the electron mass.When the average energy of a photon is counted,the rest energyis zero.From the above expression,we can see that the average energy includes all particles in the interaction region.
Table 1.Maximum density of γ-photons and positrons the number of γ-photons Nγ and positrons Ne+ ,the average energies of γ-photons and positrons and the energy conversion efficiencies from laser to γ-photons ηγ,and positronsη e+ in the cases of type I, type II.The energy conversion efficiencies in these cases are calculated with total energy of 1155.5 J.

Table 1.Maximum density of γ-photons and positrons the number of γ-photons Nγ and positrons Ne+ ,the average energies of γ-photons and positrons and the energy conversion efficiencies from laser to γ-photons ηγ,and positronsη e+ in the cases of type I, type II.The energy conversion efficiencies in these cases are calculated with total energy of 1155.5 J.
Quantity Type I Type II γ n max( ) 7.41 × 1029 m-3 5.67 × 1030 m-3+ne max( ) 2.53 × 1027 m-3 7.63 × 1027 m-3 Nγ 1.82 × 1014 1.96 × 1014+Ne 3.0 × 1010 3.15 × 1010 γ E 4.12 MeV 4.46 MeV+Ee 260.6 MeV 266.2 MeV ηγ 11.72% 13.2%η +e 8.92% 9.86%
Let us take a closer look at the process of generating electron-positron pairs under these two targets: the multiphoton Breit-Wheeler process [22, 23]

Through this process, we can find that when the density of γ-photons is high, and the number of high-energy γ-photons is large,the probability of interaction of high-energy photons with laser propagating from both sides is greater.It is obvious that the production of electron-positron pairs has increased.Of course, compared with the type I the production of positron is increased by 3 times under type II (see figure 4(b)).Besides, from the simulation results we can see that positron yields of 3.15 × 1010with an average energy at 266.2 MeV are generated under type II.However, 3.0 × 1010positrons with an average energy of 260.6 MeV are generated under type I.We summarize the important results in table 1 by comparing two targets mentioned in this simulation.
From the results of table 1, γ-photons with an average energy of 4.46 MeV are produced in type II target.In previous studies on the generation of positrons [42-44], it is reported that the positron yields of 2 × 109with the distribution peaking at 4-7 MeV and the positron density at about~1016cm-3are generated under the interaction of ~mm thick gold targets with short (~1 ps) ultraintense (~1 ×1020W cm-2) laser pulses by the Bethe-Heitler process.Their results set the highest record under the laboratory conditions at that time.Compared with their experimental results, the yield of positron in our study is nearly doubled,and the positron density is increased by five orders of magnitude.In addition,the results of this study are compared with those of some simulation studies conducted under the same method [30, 39].We find that the yields of γ-photons and positrons in this study are about 2 times and 3 times higher than their result.Moreover, the energy conversion rate of γ-photons and positrons is increased.From the simulation result,we know that the γ-ray flash duration is 10 fs,a source cross-section equal to 1λ2, and a FWHM divergence of 0.5 × 0.5 rad2.This results in a γ-photon source with an ultrahigh peak brilliance of 2 × 1025photons/s/mm2/mrad2/0.1%BW.Here,the brilliance of γ-ray is much higher than that obtained in current experiments[45,46].Such ultrabrilliant γ-photon beams would offer exciting potential capabilities and opportunities for diverse studies, such as studying nuclear phenomena and structure, discovering new particles and examining their underlying properties [47-50].
With the absorption of laser energy and the increase of hot electron energy, there are more γ-photons emitted by hot electron, attenuating the original laser wave.Thus, the conversion efficiency of the total laser energy to hot electron and photon,and finally to positron is improved.We know from the simulation results that the energy conversion rate of γ-photon reaches 13.2%in target type II.But in the first case,the energy conversion rate of γ-photon reaches 11.72%.In addition, the energy conversion rate of positron reaches 9.86%under target type II.However,in the first case,the energy conversion rate of positron is 8.92%.It is then reduced by emitting photons in a way similar to hot electrons in a laser field.Therefore, this efficient conversion of the total laser energy on the type II makes it more advantageous than type I.Thus, high density,high energy and large number of γ-photons beams and electron-positron pairs can be generated under type II.
4.Summary
In summary, we have demonstrated that the interaction of ultra-intense lasers with solid target can produce dense electron-positron plasmas and ultra-intense γ-rays.In these interactions, the main way to generate pairs is to emit γ-rays photons through a nonlinear Compton scattering process,and they are further converted into electron-positron pairs through the multiphoton Breit-Wheeler process.We compare the effects of production of γ-rays and electron-positron pairs by the interaction of two different solid targets with two counter-propagating laser beams.Compared with type I,type II has the following advantages:
(1) The density of γ-photons is increased by 7.7 times,and the positron density is enhanced by 3 times compared with those in type I.
(2) Compared with the number of γ-photons 1.82 × 1014in type I, the number of γ-photons 1.96 × 1014in type II is increased by 1.1 times,and the number of positrons is increased from 3.0 × 1010in type I to 3.15 × 1010in type II.
(3) The above simulation results demonstrate that the conversion efficiency of total laser energy to γ-photons and positron beams is higher in type II target.Since type II target has the above advantages, we believe it will be valuable in future research about the QED plasma and the generation of high-energy electronpositron plasmas and γ-ray applications.
Acknowledgments
We thank Dr Mamutjan Ababekri and Dr Amir H Sanjari for their critical reading of the paper.We are also grateful to Dr Feng Wan for his valuable discussion on this paper.This work was supported by National Natural Science Foundation of China (NSFC) under Grant No.11 875 007.The computation was carried out at the HSCC of the Beijing Normal University.The authors are particularly grateful to CFSA at University of Warwick for granting permission to use the EPOCH.
杂志排行
Plasma Science and Technology的其它文章
- First results of negative ion extraction with Cs for CRAFT prototype negative beam source
- Manipulation and optimization of electron transport by nanopore array targets
- Modulational instability of the coupled waves between fast magnetosonic wave and slow Alfvén wave in the laser-plasma interaction
- Linear gyrokinetic simulations of reversed shear Alfvén eigenmodes and ion temperature gradient modes in DIII-D tokamak
- Design and performance study of a gas-Cherenkov detector with an off-axis parabolic reflector for inertial confinement fusion experiments
- Electron population properties with different energies in a helicon plasma source
