一种基于GNSS-RTK的大跨径桥梁模态参数识别方法

潘博闻，李 志，牛彦波

（1. 天津市陆海测绘有限公司, 天津 300304；2.长江科学院，武汉 430010；3. 天津大学 建筑工程学院，天津 300350）

0 引言

全球卫星导航系统（global navigation satellite systems, GNSS）可全天候实时监测结构的3维坐标信息，测站之间无需通视，测程大，可同步测量多个测点，尤其是高采样率、多系统GNSS的发展，使得该项技术在高精度动态测量中的优势得以体现，目前已经在大型土木工程结构健康监测领域得到了广泛的应用[1-3]。实时动态差分（real time kinematic, RTK）是1种基于载波相位双差模型的定位技术，根据基线两端的相关性原理，可完全消除相对论效应误差、卫星时钟误差及接收机时钟误差的影响，且对大气折射误差、卫星星历误差有很好的抑制作用。而多路径效应主要取决于测站与反射物之间的距离、反射系数及卫星信号的方向等，即使很短的基线，RTK技术对多路径效应的抑制作用也不大，因此需要采用1种有效的数据滤波方法来削弱其所带来的影响。最新研究表明，切比雪夫滤波器在提高GNSS动态定位精度、抑制多路径效应方面有着良好的表现[4]，因此，本文设计1个5阶切比雪夫1型滤波器，来削弱GNSS传感器背景噪声带来的影响。

结构的模态参数（固有频率、振型、阻尼比）是评估结构使用性能，了解确认结构是否损伤的最基本动力参数。通常情况下，固有频率与振型是通过评估结构有限元模型的自由振动响应来确定的，而结构的阻尼比往往凭经验假定，因此结果可能存在争议。通过现场监测，从结构的响应信号中提取结构的模态参数，对于掌握结构的真实健康状况具有重要的意义。传统模态测试方法，需要在同时已知输入和输出响应的前提下，估计脉冲响应函数或频响函数，进而实现模态参数辨识[5]。对于大跨径桥梁结构而言，施加激励难度大、成本高，而且易造成结构损伤，因此，仅仅依赖结构的输出响应信号实现结构的模态参数辨识，无疑是最佳的方式，运营模态参数识别方法由此得到了发展，同时也成为了参数辨识领域中的研究热点[6]。值得注意的是，现有运营模态识别方法均假定结构的振动响应是平稳的，然而，外部激励往往是非平稳的，因此，有必要研究非平稳外激励下的模态参数识别。本文提出1种基于GNSS-RTK的大跨径桥梁模态参数识别方法。

1 大跨径桥梁模态参数识别方法

为了进一步改善运营期大跨径桥梁结构模态参数的识别精度，本文提出1种大跨径桥梁模态参数识别方法。该方法首先在RTK工作模式下，由GNSS接收机获取结构的振动响应信息；其次利用切比雪夫滤波方法，削弱传感器背景噪声的影响并得到结构的动态位移；最后采用互补集合经验模态分解（complementary ensemble empirical mode decomposition, CEEMD）与随机减量技术（random decrement technique, RDT），从滤波信号中提取结构的模态参数（固有频率与阻尼比）。

1.1 GNSS RTK获取大跨径桥梁结构振动响应信息

加速度计已经被证明是1种有效的桥梁动态变形监测方法，具有测量精度高、采集频率高、灵敏度好等特点；但是对0.2 Hz以下结构的低频振动不敏感，而且通过二次积分获取的位移会偏离真值。而GNSS接收机可直接获取结构的位移信息，尤其是多系统RTK差分定位技术的出现，使得该方法在大跨径桥梁变形监测领域得到了广泛的应用。文献[7]采用10 Hz高频全球定位系统（global positioning system, GPS）技术，对韩国某一大跨径桥梁的安全性能进行了评估，结果显示，桥面的平均挠度为8.26 mm，桥梁的频率变化为0.004 Hz，均在安全限值以内。文献[8]提出采用GPS与北斗卫星导航系统（BeiDou navigation satellite system, BDS）双频测量技术，对1座大跨径悬索桥进行现场实验，结果显示，相比GPS单系统，双系统组合定位技术的精度提高了20%～30%，得到了可靠的桥梁动态变形监测信息。本文使用的GNSS接收机可同时接收GPS、BDS与格洛纳斯卫星导航系统（global navigation satellite system, GLONASS）三个卫星导航系统的导航卫星信号，为获取结构的高精度振动响应信号提供了可靠的依据。

1.2 切比雪夫滤波方法削弱传感器背景噪声的影响

多路径误差主要位于监测信号的低频部分，低频噪声较高频噪声对结果的影响更为显著；因此本文拟采用切比雪夫1型高通滤波器，来削弱传感器低频背景噪声的影响。该滤波器的幅值二次响应函数可以表示为

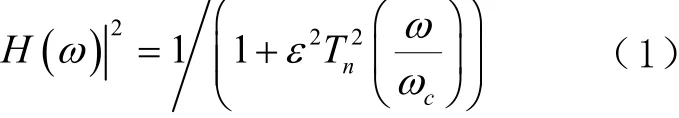
式中：ε为通带内幅度波动的程度，ε越大，波动幅度越大；为阶切比雪夫多项式；ω为有效通带截至频率；cω为通带波纹。

1.3 互补集合经验模态分解算法消除噪声引起的重构误差

集合经验模态分解（ensemble empirical model decomposition, EEMD）算法[9]能够将1个非平稳、非线性信号分解为一系列具有明确定义的、从高频至低频排列的准稳态固有模态函数（intrinsic mode function, IMF）分量。每1个IMF分量含有的频率成分，不仅与原信号的分析频率有关，而且具有自适应的特点，具有很高的信噪比。互补集合经验模态分解CEEMD方法是针对EEMD方法中，由白噪声引起的重构误差提出的1种信号处理方法，通过在原始信号中引入成对的正负辅助噪声来去除重构信号中的残余辅助噪声。这样做还能够减少引入的噪声集合次数，提高运算效率[10]。其具体分析步骤如下：

1）在原始信号y(t)中添加一组白噪声序列η±(t)，形成2个新的信号Y±(t)，即

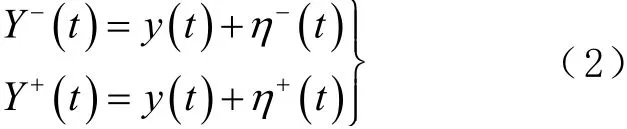
利用经验模态分解方法（empirical model decomposition，EMD）对式（2）进行分解，假定每个信号经分解后得到N个IMF分量，则总共会得到2N个IMF分量[11]；

2）通过对多个IMF分量进行平均运算，得最终结果，即

值得注意的是，在IMF分量中，可能存在有噪声引起的虚假模态，1个简单的解决办法是利用式（4）计算每阶分量与待分解信号的相关系数ρ，相关系数小于0.1的，就被视为虚假分量予以剔除，即

式中：c ov ( IMFi(t),y(t))是第i阶IMF分量与原始信号y(t)的协方差；σIMFi(t)与σy(t)分别是第i阶IMF分量与原始信号y(t)的标准差。

1.4 随机减量技术提取结构模态参数

随机减量技术是1种简单且有效的时域信号预处理方法，该方法通过对结构振动响应信号进行多段截取，并对截取信号进行总体平均运算，来去掉信号中的随机部分；进而可得到监测信号中的确定性部分，即自由衰减信号（random decrement signal, RDS）R(τ)[12]；最后可利用对数衰减法，从自由衰减信号中提取结构的模态参数。R(τ)的表达形式为

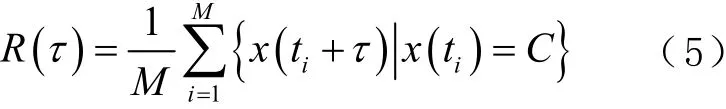
式中：x(t)为位移响应信号；x(ti+τ)为划分的时间样本函数；M为样本数；C为x(t)在时刻ti处的初始条件。

结构的模态频率ω可以表示为

式中T表示自由衰减信号循环1次得到的平均周期。

阻尼比ξ可以通过求解方程得到，即

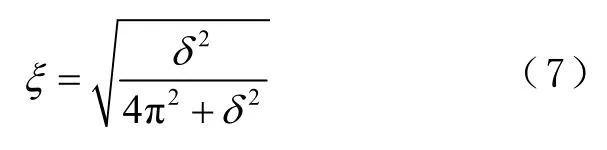
式中δ表示对数衰减率，其计算方法为

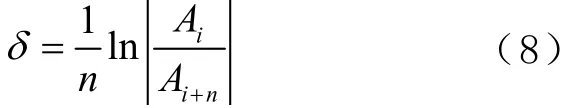
式中：iA、Ai+n分别为自由衰减信号第i次与第i+n次循环的幅值。

2 实验与结果分析

2.1 实验方案

选择天津市彩虹大桥作为研究对象，该桥是1座三跨钢管混凝土拱桥，全桥长1 215.69 m，主桥长504 m，桥宽29 m，计算跨度160 m，如图1所示。

图1 天津市彩虹大桥

迄今为止，远远超过了设计荷载的超重车辆的长期通行，对彩虹桥造成了严重损害。2010年6月，主桥的1个纵向混凝土梁开裂，导致相邻2个纵向混凝土梁受到不同程度的损坏。一份检查报告显示，这座桥存在安全隐患。随后，用组合梁替换了所有纵向混凝土梁，并限制大型卡车通行。

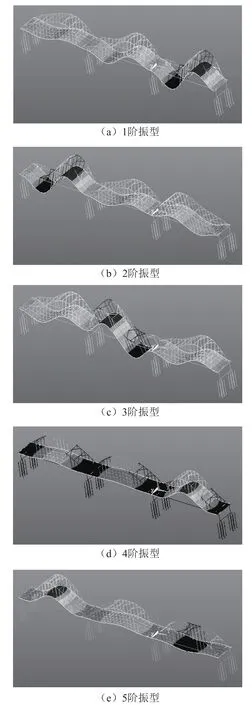
图2 天津市彩虹大桥有限元模态分析结果

在进行现场监测之前，首先利用安西斯（Ansys）有限元分析软件，建立了桥梁的3维有限元模型，预测了结构前6阶竖向振型，如图2所示。相应的模态频率分别为0.678 7、1.036 1、1.4171、2.125 4、2.322 5、2.694 5 Hz。在此模型中，钢管、风撑、横梁、纵梁和桥墩均采用BEAM44单元进行模拟，系杆采用LINK10单元进行模拟，桥面板采用SHELL63单元进行模拟，共计1 765个结点，2 727个单元，每个结点有6个自由度，即沿x、y、z轴的平移与绕x、y、z轴的旋转。

观察有限元分析结果可知，变形极大值出现在每跨的1/4处、1/2处及3/4处，在变形极大值处布置传感器，可以有效的反映结构的振动特性，获取到结构较多的振动模态。因此，现场监测尝试采用10台高频GNSS接收机，将其采样率设置为50 Hz，用来监测结构在正常运营状态下的振动响应。根据奈奎斯特采样定理，当采样频率大于信号中最高频率的2倍时，采样之后的信号能完整地保留原始信号中的信息，本文采用50 Hz是能充分满足要求的。GNSS接收机现场布置如图3所示。其中，1台GNSS接收机作为参考站，通过三脚架固定在坚实的地面上，距离主桥约120 m，如图3（a）所示；其余9台GNSS接收机作为移动站布置在桥的一侧，如图3（b）所示，共计9个测点，其编号为C1、C2、C3、C4、C5、C6、C7、C8及C9。实验时间为2019:07:10 T 09:00—18:00，连续监测9 h。

图3 GNSS传感器现场布置

2.2 数据处理与分析

选取主跨跨中测点进行分析，其余测点类似，不再赘述。图4（a）与图4（b）给出了GNSS接收机原始观测数据及相应的功率谱密度（power spectral density, PSD）分布图。·

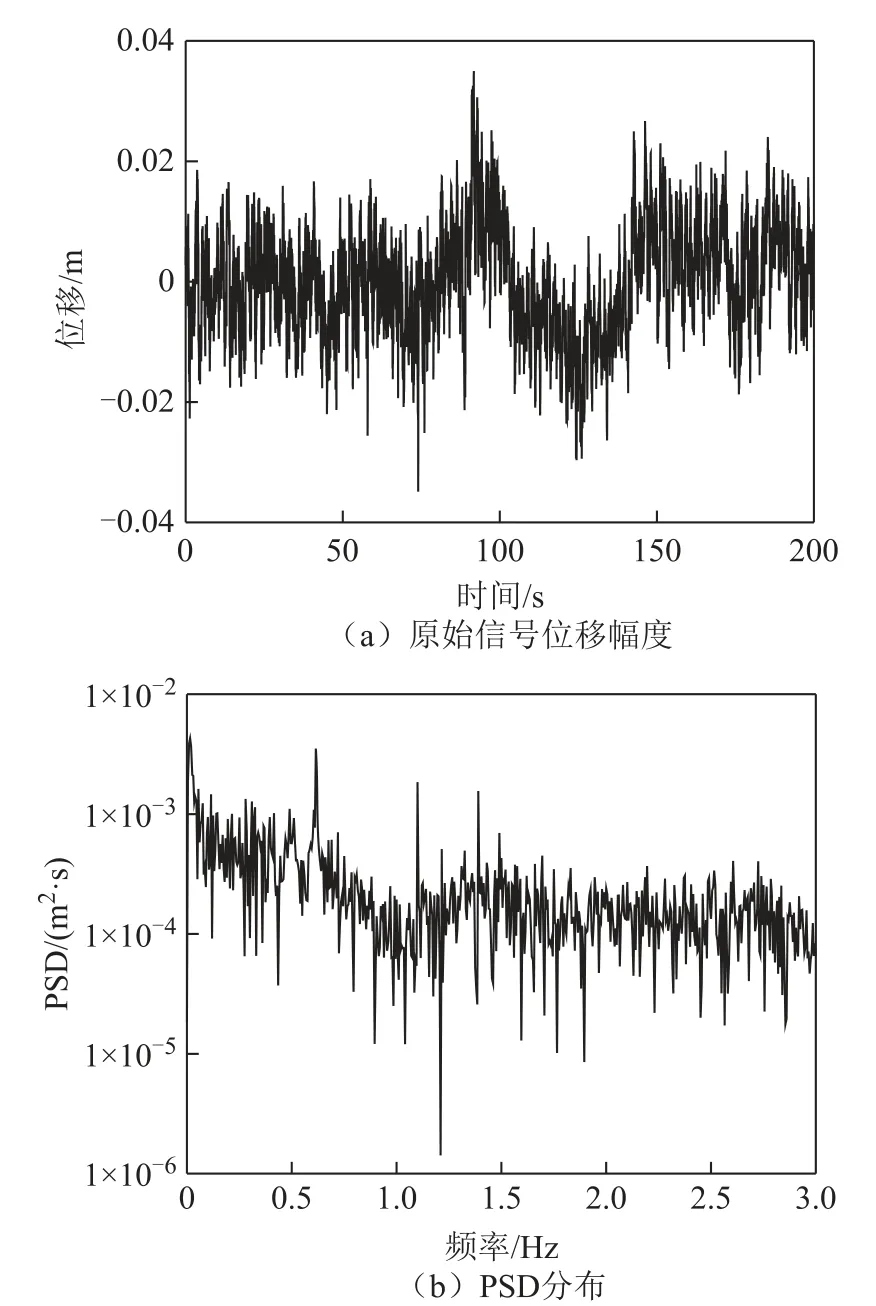
图4 原始观测信号与相应的PSD分布

从图4可以看出：位移在-0.034 9与0.035 0 m之间变化，PSD图中存在明显的3处峰值对应结构的前3模态频率，分别为0.616 9、1.096 0与1.389 9 Hz。与有限元模态分析结果相比，二者基本吻合。

采用5阶切比雪夫1型高通滤波器，可削弱传感器低频背景噪声的影响。值得注意的是，在削弱噪声的同时，也移除了结构的准静态位移，剩下的仅仅是结构的动态振动部分，结果如图5所示。与原始信号相比，位移幅值明显降低，在-0.024 7与0.025 3 m之间变化。滤波前后信号的均方根值（root meam square，RMS）分别为0.009 1与0.007 2 m。

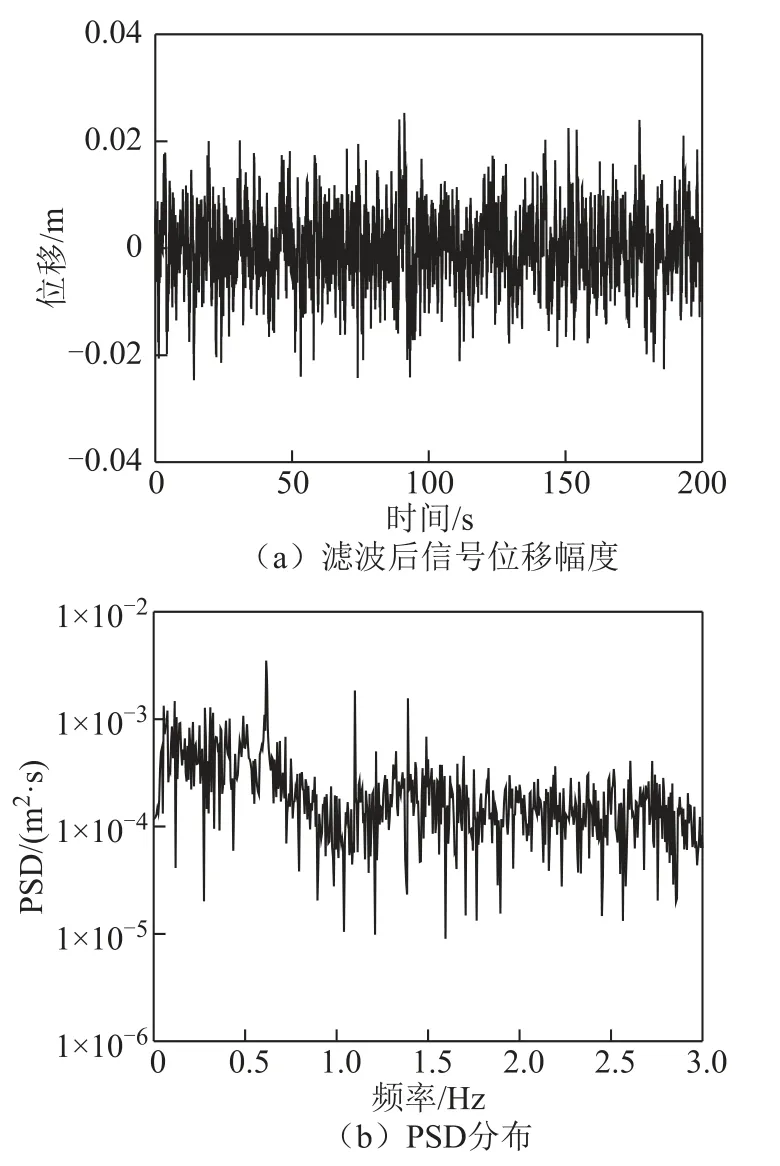
图5 切比雪夫滤波信号与相应的PSD分布

利用CEEMD法分解图5（a）所示滤波信号，得到13阶IMF分量，如图6所示。利用式（3）求每阶分量与滤波信号的相关系数，结果如表1所示。

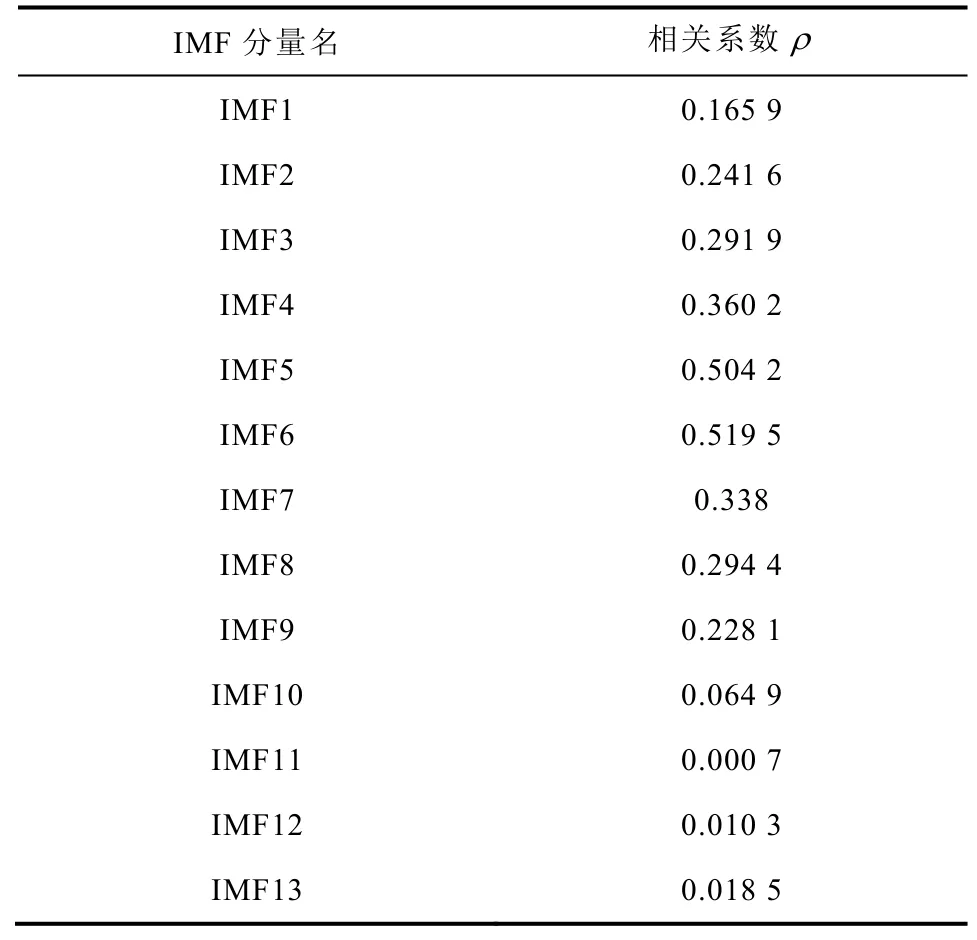
表1 待分解信号与每阶IMF分量的相关系数

由表1可以看出：最后4阶分量与滤波信号的相关系数小于0.1，视其为虚假分量予以剔除；对其余分量利用快速傅里叶变换（fast Fourier transform, FFT）算法，求其功率谱密度函数，可知前3阶模态主要存在于IMF4、TMF5及IMF6分量中，因此仅仅用这3阶分量来进一步获取结构的阻尼信息。

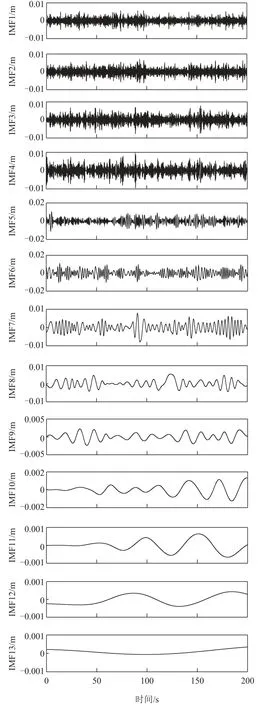
图6 经CEEMD分解后所得IMF分量的时程曲线

利用RDT法从IMF4、IMF5及IMF6分量中，提取结构的自由衰减信号，其结果如图7（a）、图7（b）及7（c）所示。

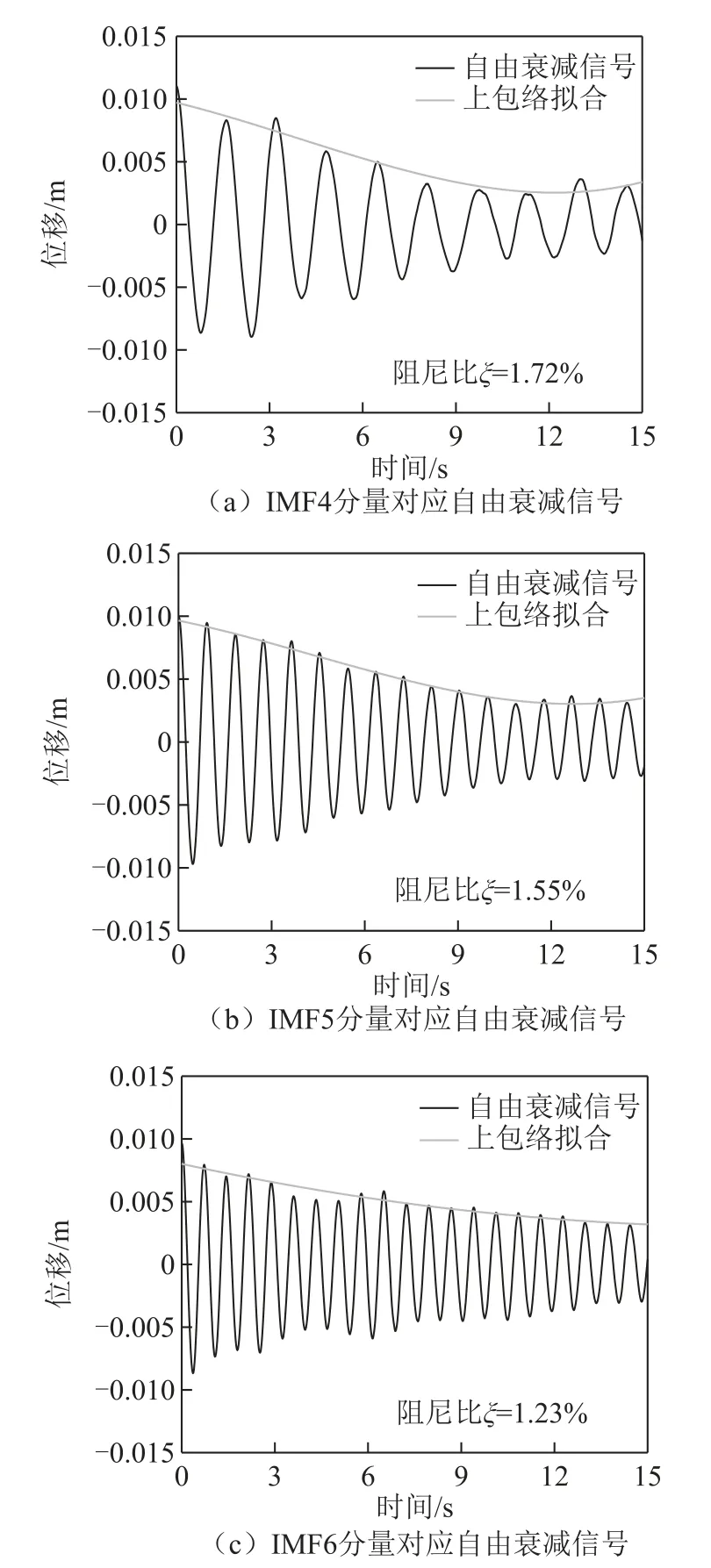
图7 从IMF分量中提取的自由衰减信号的时程曲线

需要注意的是，利用RDT法提取结构的自由衰减响应信号，截取时间的选取是十分重要的：如果时间取的过大，在衰减的后期会出现波形畸变，相对偏差也会比较大；如果时间取的过小，则会出现由于计算衰减曲线的点不足而导致拟合结果精度低的情况，为了尽可能获取理想的拟合精度，需要进行反复尝试。本文设置截取时间为15 s，并进一步基于式（7）得到结构的阻尼比，分别为1.72%、1.55%与1.23%。至此，成功得到了结构的前3阶模态频率与阻尼比。

3 结束语

本文利用GNSS-RTK传感技术对运营期1座大跨径桥梁结构振动响应进行现场实时监测，提出1种基于GNSS-RTK的大跨径桥梁模态参数识别方法。利用该方法从桥梁振动响应信号中，成功地提取了结构的前3阶模态频率与阻尼比，验证了算法的有效性；同时也说明，GNSS-RTK技术可有效地应用到大跨径桥梁振动响应的监测中。