基于改进遗传算法的图像分割

胡承刚，高建瓴，喻明豪，白羽飞，陈 楠

（贵州大学 大数据与信息工程学院，贵阳 550025）

0 引 言

遗传算法最早由美国Michigan 大学的教授John Holland模拟生物遗传和进化提出［1］。二十世纪80 年代，De Jong 基于遗传算法的思想在计算机上进行数值优化实验，归纳总结形成其基本框架。遗传算法通过将目标函数的自变量映射为生物遗传进化中的染色体，对染色体编码来实现向下进化，并找到使目标函数最优的染色体；同时，遗传过程中加入了交叉和变异操作，来优化下一代染色体。遗传算法中染色体的编码方式有浮点数编码和二进制编码两种方式。不同的染色体编码方式和采取的变异算子、交叉算子的差异同样造成了遗传算法不同［2］。由于遗传算法是一种全概率搜索优化算法，所以其对于目标函数的性质没有要求，比如：可微、连续等，所以在很多实际问题中都有应用，比如：数值函数寻优、多目标优化、机器学习、图像处理，最优路径规划、神经网络的训练等。

图像分割是区分图像中的对象和背景的过程。对于许多依赖于计算机视觉的应用，如医学成像、卫星图像中的物体定位、机器视觉、手指打印和人脸识别等许多应用来说，图像分割是一项必不可少的预处理任务。图像分割的准确性将对图像处理的后续阶段的有效性产生很大的影响。图像分割问题已被研究数年，但由于图像的不同模态直方图等特征，图像分割问题仍是一个有待进一步研究的问题。基于深度学习的图像分割虽然有不错的效果，但是需要大量标注数据来训练神经网络；基于阈值分割的Otsu 是经典的图像分割算法，在单阈值分割时算法效率很高，但在多阈值分割时算法的速度极低，这是由于算法会遍历图像的每个像素点，计算类内方差和类间方差，算法速度慢；基于遗传算法的阈值分割可以解决多阈值图像分割效率低的问题。

本文分析遗传算法及其改进算法的性能，提出一种混合改进的遗传算法，并将改进的算法先用于数值函数寻优，以测试比较改进算法的性能；对图像阈值分割进行分析，找到最佳的阈值来分割图像，OTSU 算法遍历像素的操作在多阈值分割时性能下降严重，通过对阈值分割算法分析，使用遗传算法来寻找最佳阈值，以分割图像。

1 混合改进的遗传算法

1.1 自适应遗传算法模型

遗传算法在多个领域的研究表明其高效性，其性能取决于在迭代的最后是否能够在函数优化中收敛到局部或者全局最优解。标准遗传算法（SGA）采用固定控制参数方法，即固定交叉概率和变异概率，缺点明显，因为前后期适应度不同，所以需要的交叉、变异概率也不同。赵大兴等人提出基于适应度对交叉、变异概率作出改进，改进的选择算子会根据个体适应度之间的相似性把种群分为若干组，以组为单位进行轮盘赌选择，在选中的组中产生新的个体［3］；陈璐等人将遗传算法分解为两部分，通过第一次寻优找到优秀个体，将最佳个体再次放入第二个种群中，得到最后的最优解［4］；江涛等通过在适应度函数中加入路径平滑度来改善遗传算法［5］；陈友青等人提出一种改进算子的遗传算法［6］。虽然这些研究在一定程度上改善了遗传算法的性能，但是使用固定交叉概率和变异概率的方式固化了参数，算法前期和后期染色体使用的交叉概率、变异概率一样，算法收敛速度问题依旧没有得到很好的解决。

针对遗传算法参数固定带来的问题，M.Srinvas和L.M.Patnaik 提出了自适应遗传算法（Adaptive GA，AGA），其思想是在迭代过程中根据种群适应度来自适应的调整交叉概率和变异概率［7］。公式（1）如下：

式中，pc，pm分别表示交叉概率和变异概率；fmax为当代种群最大适应度值；表示当代种群的平均适应度值；f表示变异个体的适应度值；f ′表示交叉两个体中较大的适应度的值；ki（i＝1，2，3，4）为常数，取值范围0＜ki≤1。

AGA 解决了算法前期和后期适应度高的个体和适应度低个体的交叉概率、变异概率相同的缺点。但自适应遗传算法没有从全局出发来控制交叉概率和变异概率，所以在算法后期容易陷入局部收敛，难以找到全局最优解。针对这个问题，曲志坚等人提出在算法进化过程中使用优秀个体代替适应度差的个体［2］；刘芳等人提出基于种群多样性的IAGA 来改善算法后期易陷入局部最优解的问题［8］；闫春等人使用反正弦函数自适应调节变异概率［9］。

通过对遗传算法以及各种改进方式的对比研究，本文提出了混合改进遗传算法：根据种群密度和进化代数的协同性，改进交叉概率；通过对种群密度的统计，提出基于种群密度调整变异概率。

1.2 混合改进自适应遗传算法

1.2.1 改进交叉概率

评价算法性能指标可以用进化性来指导，更好的下一代比上一代更能适应环境变化。评价算法进化性可以使用种群的密度来衡量，本文算法中计算每一代群体密度计算方式（2）如下：

分析每一代种群密度的变化可以掌握算法性能，受改进的自适应遗传算法（IAGA）［10］的启发，在种群密度的基础上加上进化代数的因素，从种群迭代次数以及种群集中程度的考量，改进交叉概率，公式（3）如下：

其中，ρ1表示当前种群的集中程度，t是当前种群的进化代数。

1.2.2 基于种群中心区域密度改进变异概率

在算法进化的后期，种群內部已经趋于相对稳定的状态，若算法此时得到的解是局部最优，由于状态稳定，算法难以发生实质进化和走出局部最优解，如图1 所示。自然界中的各种生物会经历“天灾”这样的自然灾害，基于这种思考，选择设置类似于自然界中的“天灾”设定，一定程度上将旧种群初始化为新的种群，从而走出此处局部最优解，并试图寻找下一个可能的局部最优解，从而使模型更有希望与能力达到全局最优解。算法遭遇“天灾”之前，变异概率随之下降，同时设置“天灾”发生后在正常的种群中心区域密度ρ2下，密度越高时，变异概率也会随之上升。

图1 种群密度变化图Fig.1 Change of population density

为计算种群中心区域的密度ρ2设定参数：M表示群体所含的个体数目；fmax为种群最大适应度；fmin表示种群最小适应度；favg表示种群平均适应度，则t代种群的范围M（H，t）如式（4）：

某个体的适应度到群体适应度均值之间的距离m（h），式（5）：

群体中心区域的半径σ可以表示为式（6）：

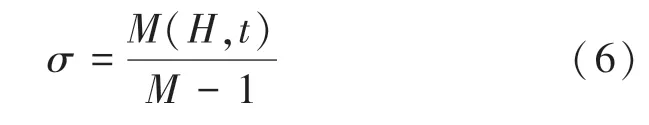
某染色体适应度到当代群体适应度均值的距离小于σ的染色体数目N（δ，f），则群体中心的密度ρ2为式（7）：

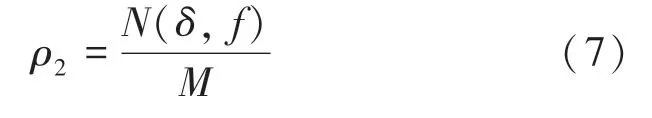
通过对种群中心区域密度的分析，对变异概率改进如式（8）：

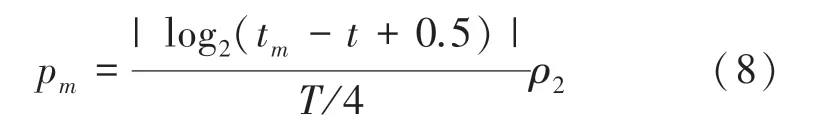
式中，T表示最大进化次数；t表示当前进化次数；tm是经历“天灾”的某代种群。

文中设定当中心区域密度达到0.5 时，种群经历“天灾”，之后变异概率会逐渐上升，如图2 所示。

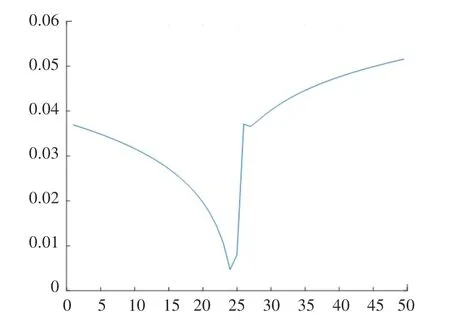
图2 变异概率变化曲线Fig.2 Variation curve of mutation probability

2 仿真实验结果

本文仿真实验基于Windows 10（x64）操作系统，Intel（R）Core（TM）i5－7500 CPU 3.40 GHz主频，RAM8G内存。编译环境采用MATLAB R2018a。12 个函数的形式，寻优范围和函数最优值见表1。使用12 个测试函数来对本文改进后的算法进行仿真测试，其中函数F2、F3、F5、F7－ F11 拥有许多局部极小值，F1、F4、F6、F12 用于多维空间测试。

表1 测试函数Tab.1 Test functions

实验对表1 中的函数在搜索空间中进行优化测试，对比算法选择SGA 以及IAGA，SGA 参数设置：pc＝0.7、pm＝0.01；IAGA 参数设置：pc1＝0.9，pc2＝0.6，pm1＝0.1，pm2＝0.001。使用12 个函数对算法进行2 维寻优性能测试分析，函数F1、F6、F10、F12 进行30 维测试。

2.1 改进算法性能测试

在2 维情况下，将SGA，IAGA与本文算法在12个测试函数上进行试验，3 种算法独立求解测试函数所得收敛曲线如图3 所示，从F1～F5 函数在算法迭代50 次寻优的曲线，可以看出本文算法在函数F1～F5 上都能近似到最优效果；同时图3 还给出了F6～F12 函数迭代200 次的寻优效果，可以看出本文算法收敛速度明显快于SGA 和IAGA。由图3 可以看出，通过种群密度和迭代次数的全局考虑，以及加入类似“天灾”设置的情况下，算法收敛速度快，易跳出局部最优值，而其余两种算法则出现收敛速度慢或陷入局部最优解等问题。虽然本文算法在前期函数F3 收敛速度略劣于前两种算法，但是在中后期收敛速度明显高于前两种算法，对比来看本文算法更具优势。

图3 测试函数适应度变化曲线Fig.3 Fitness curve of test function

2.2 收敛精度与收敛率分析

实验使用了表1 中测试函数F1～F6，进行了50 次独立测试，测试结果见表2。可以看出本文算法在50 次独立实验中收敛精度上优于其余两种算法，收敛率（在50 多次独立实验中的收敛次数）也明显高于其余两种算法，函数F3在50 次实验中收敛次数也高于前两种。30 维搜索空间优化实验中改进算法对比SGA 和IAGA在收敛速度和跳出局部最优解能力更有优势，收敛曲线如图4 所示。

图4 30 维搜索空间测试结果Fig.4 Test results of 30－dimensional search space

表2 函数F1～F6在50 次独立实验的200 代平均值以及收敛率对比Tab.2 Comparison of average and convergence rate of function F1～F6 in 50 independent experiments with 200 generations

3 改进遗传算法图像分割

3.1 Otsu 图像分割

图像分割是计算机视觉中一个重要的研究内容，在很多领域中都是一项必不可少的图像预处理任务。基于阈值分割的大律法（Otsu）是经典的图像分割算法，但是在多阈值分割任务上性能很差，处理图像时间长，所以本文使用改进遗传算法用于阈值图像分割。图像阈值分割经典算法是Otsu 算法，通过寻找灰度图像中的最佳阈值来分割图像，虽然在单阈值分割时Otsu 算法表现不错，但是多阈值分割时一张图像需要处理的时间过长，算法效率太低。使用改进的遗传算法用于图像分割，流程图如图5。

图5 改进算法用于图像分割流程图Fig.5 Flow chart of improved algorithm for image segmentation

单个阈值把图像像素分为两类，Otsu 算法通过遍历每个像素点寻找能最大化类间方差的点，这个像素点就是最佳阈值。多阈值是在单阈值的基础上推广而来。若有M个阈值（t1，t2…tM）将图像分为M＋1 类（C0，C1…CM），分割标准的度量可以使用类间方差和类内方差共同决定。类内方差尽可能小，类间方差尽可能大，衡量标准则是类间方差和类内方差比值，式（9）：

其中，Sbb是类间方差，Swo是类内方差。

选取公式（9）为适应度函数，转换为函数寻优中的求最大值问题。灰度图像的像素级在［0，255］之间，阈值就是灰度值，将染色体编码为比特向量，每一个向量都有L ×M位，L是log（灰度级数），M是阈值数，则每L位表示一个染色体，如图6 所示。

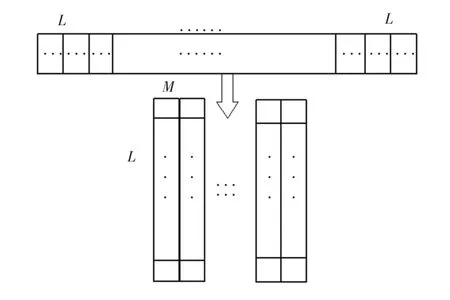
图6 像素编码为染色体Fig.6 The pixels are encoded as chromosomes

3.2 图像分割实验

Otsu 算法在多阈值分割时出现分割速度慢、抗噪性能差的缺点，采用改进的遗传算法优化Otsu 多阈值分割，能在一定程度上克服这些不足之处，实验结果见表3、如图7 所示。使用原Otsu 算法、SGA、IAGA 以及本文改进的算法对图像进行分割，传统Otsu 算法分割效率低；遗传算法的加入解决效率低的问题，但由图7 的实验结果来看，SGA、IAGA 算法还有明显的噪声，在细小部分分割效果差。使用遗传算法分割图像在单阈值和多阈值时所用时间对比见表3。

图7 图像分割结果Fig.7 Image segmentation results

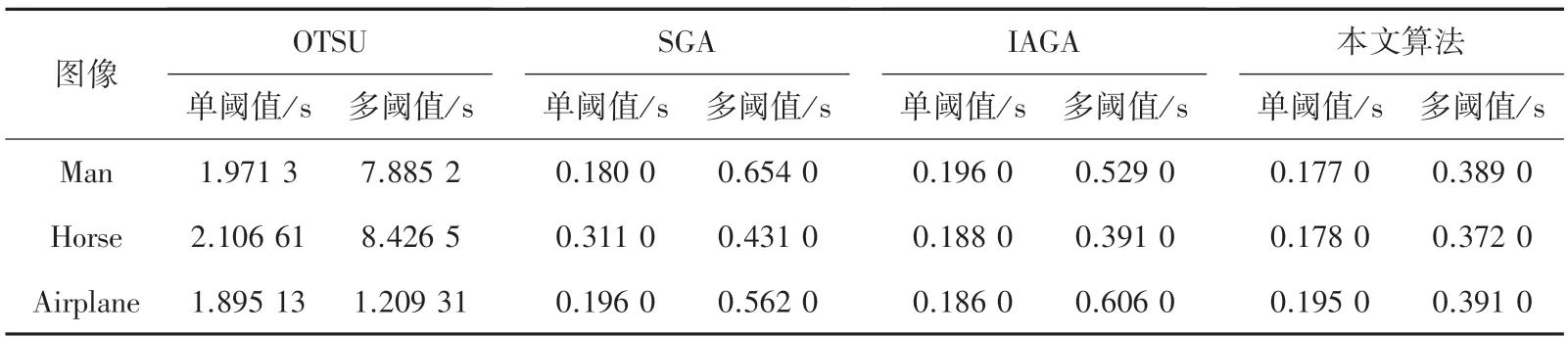
表3 四种方法分割时间对比Tab.3 Comparison among the four methods on time consumption

4 结束语

针对标准遗传算法在进化过程难以跳出局部最优解、收敛率较低和收敛速度慢等问题，本文通过以下两种方式改进遗传算法：首先，考虑种群密度和进化代数的协同性，改进交叉概率，以增强交叉概率自适应性；其次，在进化过程中又设定类似于“天灾”设置，结合进化代数改进变异概率，增强种群跳出局部最优解的能力。相较于简单遗传算法和自适应遗传算法，本文算法在收敛速度和收敛率上有明显优势，在跳出局部最优解的能力上也优于SGA 和IAGA。通过改进算法分割图像也达到不错的效果，相较于传统的Otsu 算法，结合遗传算法优化之后效果更好，在与IAGA、SGA 优化对比中，本文改进算法更具有鲁棒性，抗噪能力更强。