基于改进密度的簇内均值最小距离聚类算法

段桂芹

（广东松山职业技术学院 计算机与信息工程学院，广东 韶关 512126）

0 引 言

聚类的目标是将同一簇中样本相似度最大化，不同簇间样本相似度最小化。根据聚类过程的不同，通常将聚类分成基于密度、划分、模型、网格、层次5 种聚类模型［1－2］。作为经典的基于划分模型的聚类算法，K－means 具有计算便捷、易于理解等特点［3］，由于K－means 算法的初始聚类中心选取是随机的［4］，因此极易出现局部最优，导致聚类结果不稳定。此外，当样本中存在噪声或离群点时，聚类中心与真实中心存在较大偏差，易生成较差的聚类结果［5－6］。

1 相关算法研究现状

为了解决聚类分析中的问题，研究者们提出了多种改进算法。Zhai 等人［7］根据相距最远的数据对象不会划分至同一簇的基本思想，使用最大距离选取初始聚类中心，解决了原始算法更新次数多、耗时长等问题。在此基础上，段桂芹［8］将最大距离乘积法与K－means 算法相结合，用相对分散的数据对象构造簇中心集合，优化了初始聚类中心，该方法在一定程度上解决了聚类结果不稳定等问题，但依然存在迭代次数多、运算耗时长等现象。邹臣嵩［9］针对文献［8］的这一问题，提出了一种协同K 聚类算法。该算法通过样本的分布情况统计其密度参数，选取与样本集中心点最远的高密度对象为首个聚类中心，再通过最大乘积法求得其余聚类中心。徐红艳等［10］提出基于网格划分的快速确定全局阈值算法。该方法通过网格划分思想，将数据自适应地划分到多个网格空间中，再利用密度估计来计算密度，进而实现快速查找类簇峰值和低谷，最终完成数据集的有效识别。虽然文献［7－10］在一定程度上优化了K－means 算法的初始聚类中心选择过程，但对噪声的影响有所忽略。潘品臣［11］根据密度参数理论，对数据集中的高密度点和非离群点区域进行了计算与识别，规避了选取噪音点为初始聚类中心以及中心分布不理想等问题。卜秋瑾［12］针对密度峰值聚类算法处理多密度峰值数据集时，人工选择聚类中心易造成簇的误划分问题，提出一种结合遗传k均值改进的密度峰值聚类算法。该算法能找到准确簇个数同时避免算法陷入局部最优，在提高聚类质量的同时，保证了聚类质量的稳定性。陈奕延［13］将样本涵盖的经典信息拓展到了模糊集上，利用寻找密度峰值的方法对模糊样本进行聚类，提出了误差更小的针对连续型模糊集与离散型模糊集的改进型欧氏距离，使改进后的欧氏距离具有更小的误差。

在对上述文献分析研究的基础上，本文从密度聚类算法入手，从两个方面对密度聚类算法进行了改进：一是根据高密度样本被低密度样本紧密围绕这一思想，提出了新的密度计算方法。目的是提高聚类中心的代表性，解决密度参数选取敏感等问题。二是在簇更新阶段，将与簇内均值距离最近的样本点作为该簇的临时中心，减少了迭代次数，降低运算耗时。

2 密度聚类算法改进

改进的密度聚类算法，由初始中心选择和簇中心迭代计算两部分构成。

（1）初始中心选择：首先使用自定义密度公式获取各样本密度，将高密度样本作为聚类中心候选代表点，并生成候选代表点集合；在集合中选取与其他候选代表点距离和最小者作为首个初始聚类中心，再使用乘积最大法完成初始聚类中心选择，得到初始聚类中心集合，即Z＝｛z1，z2，…，zk｝。

（2）簇中心迭代计算：根据集合Z完成初次聚类，计算簇内各样本到簇均值中心的距离矩阵。为了降低均值法所得簇中心和实际簇中心位置间的偏差，将与簇内均值距离最近的样本作为该簇的临时中心，生成临时簇中心集合，即Z＝，再通过最小距离法将相关样本划分至所属簇中。重复簇中心迭代计算过程，直至准则函数收敛，完成聚类。

2.1 基本概念与公式

设X为含有n个样本的数据集，X＝｛x1，x2，…，xn｝，样本的属性个数为p，xi＝。X划分为k个簇，X＝｛C1，C2，…，Ck｝，｜Ci ｜表示第i簇所含样本个数，zk表示第k簇的中心，多个簇中心所构成的集合为Z，即Z＝｛z1，z2，…，zk｝。

定义1任意两样本间的欧氏距离为：

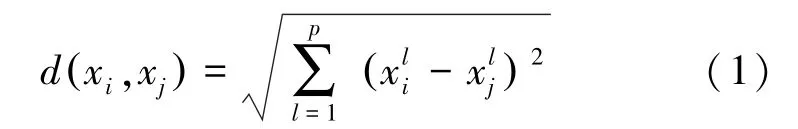
其中：i＝1，2，…，n；j＝1，2，…，n；l＝1，2，…，p

定义2任意样本xi的距离和定义为：该样本到数据集各样本的距离之和。

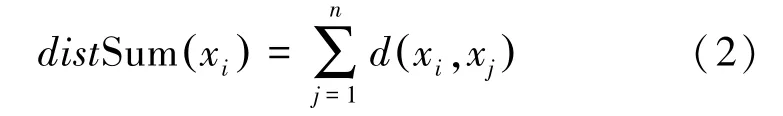
定义3样本xi的密度为：

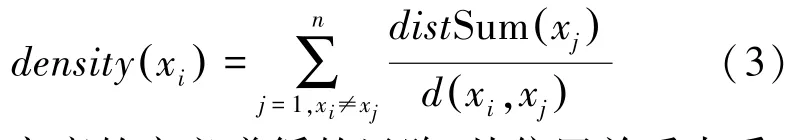
本文密度的定义遵循的思路：从位置关系来看，当某个样本xi被其它样本紧密围绕时，说明该样本与其它样本间的距离和相对较小；反之，当样本xi和其它样本的位置关系较为分散时，说明该样本与其它样本间的距离和相对较大。密度表达式用样本xi和xj之间的距离做分母，用xj到全部样本的距离之和做分子，用二者距离比值的累加和表示样本xi被其它样本围绕的紧密程度，即xi的密度。

以样本xi为例。当式（3）累加和中的分子较大时，意味着除xi外其它样本的累加距离和也较大；当分母较小时，意味着xi到其它样本距离的累加和较小。因此，当分子越大且分母越小时，表达式的值越大，说明xi被比自身密度低的样本所围绕的密集程度越大，即xi的相对密度越大，其作为簇中心的代表性越强。

定义4样本集的平均密度定义为：

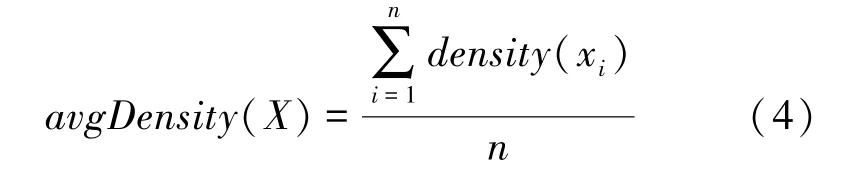
定义5候选代表点集合定义为：密度高于样本集平均密度α倍的样本集合

其中：xi，xj∈Ct，t＝1，2，…，k。

定义6候选代表点间的距离矩阵定义为

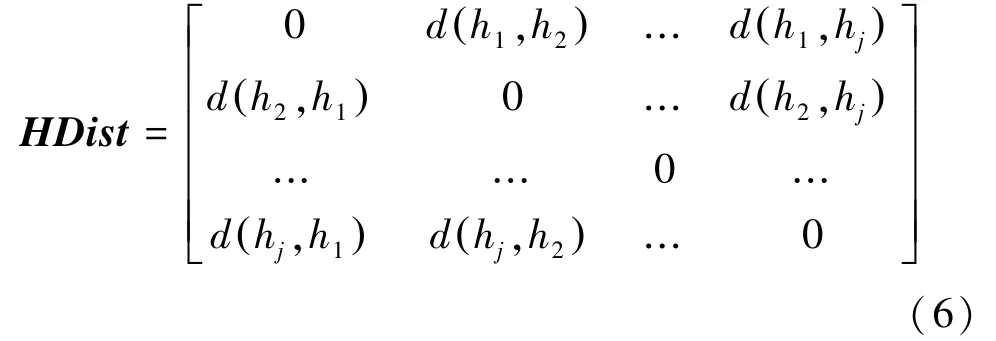
式中，j表示集合H所含元素个数。

定义7簇内样本与本簇均值中心间的距离矩阵定义为：

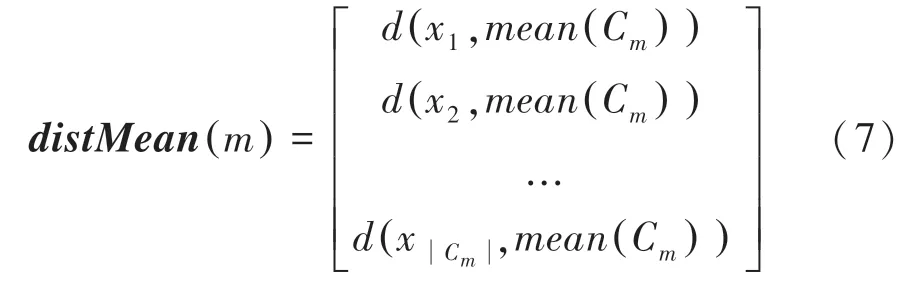
式中，m＝1，2，…，k，Cm表示第m簇的样本集合。

定义8簇更新后，将与簇内均值距离最近的样本xi作为该簇的中心。xi满足以下条件：

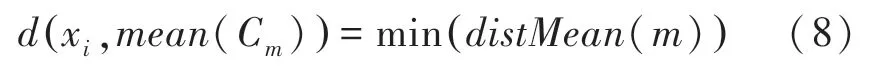
定义9聚类误差平方和E的定义为

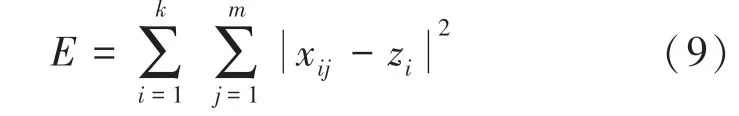
式中，xij为第i簇中第j个样本，zi为第i簇的簇中心。

2.2 算法描述

步骤1使用式（1）～式（3）计算各样本的密度；

步骤2使用式（4）、式（5）得到候选代表点集合H，其中参数α为1.0；

步骤3用式（1）、式（6）计算候选代表点间的距离矩阵，在H中选择与其它候选代表点距离和最小者作为首个聚类中心z1存储至集合Z中；

步骤4在集合H中选择与z1距离最远的候选代表点z2存储至集合Z中；

步骤5从集合H中选择满足条件：max（d（hi，z1）×d（hi，z2））的代表点，作为z3存储至集合Z中；

步骤6重复运行步骤5，直至｜Z ｜＝k；

步骤7使用式（1）计算X中各样本与集合Z中各候选点的距离，并划分至距离最小的簇中；

步骤8使用式（7）计算簇内各样本到簇均值中心的距离矩阵，根据式（8）将距离簇内均值最近的样本作为该簇的新中心；

步骤9重复步骤7、8，更新簇中心集合Z；

步骤10将X中的样本按距离划分至最近的簇中，使用式（9）计算并判断E是否收敛，若收敛，则算法终止；若未能收敛，将跳转至步骤7，再次更新簇中心。

2.3 算法复杂度分析

本文算法的时间复杂度为O（n2＋nkt），在初始聚类中心选择过程中，本文算法首先计算了各样本的密度，进而得出候选代表点集合，再使用距离乘积最大法对候选点从空间分布的角度进行了二次筛选。虽然计算量有所增加，但各中心的代表性得到增强，初步反映了样本集的几何结构，为簇更新次数的降低提供支撑。在簇中心更新过程中，本文算法选取与簇内均值距离最近的样本作为该簇的临时中心，生成了临时簇中心集合，避免了均值法所得簇中心和实际簇中心位置存在偏差的隐患，相比均值算法，本文算法可以降低噪音的干扰，减少更新次数，降低计算开销，提高运算效率。

3 实验仿真与分析

实验运行环境：CPU Intel Core i7－ 2670 2.20 GHz，硬盘1T，内存8G；操作系统Win10－64位；仿真软件采用Matlab 2011b。在有效性验证方面，采用聚类准确率、聚类各阶段开销、Rand 指数、Jaccard 系数等指标，将K－means 算法、文献［8］中算法、文献［9］中算法与本文算法进行了比较。实验过程中，K－means 算法共运行200 次，取其平均值作为该算法的实验结果。实验数据集详见表1。

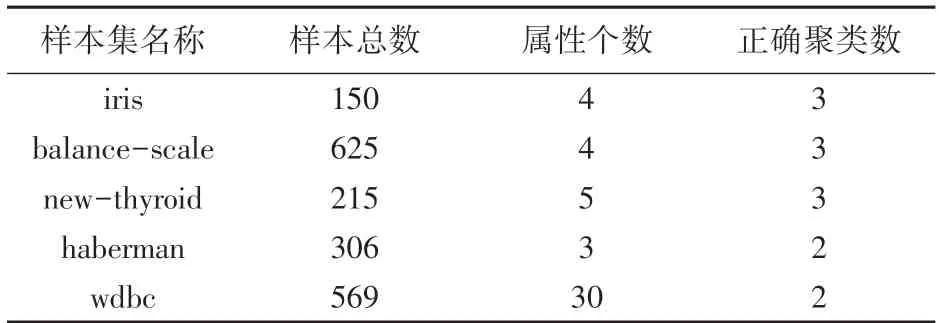
表1 UCI 数据集Tab.1 UCI dataset

3.1 算法性能对比与分析

图1～图5 是K－means 算法、文献［8－9］算法以及本文算法的聚类准确率、簇中心各阶段计算开销、簇更新次数等实验的对比结果。由图1 可知，在iris和wdbc 数据上，本文算法的聚类准确率明显高于K－means算法，略高于文献［8－9］算法，在balance、thyroid 和haberman 数据集上的聚类准确率优于其它3 种算法。

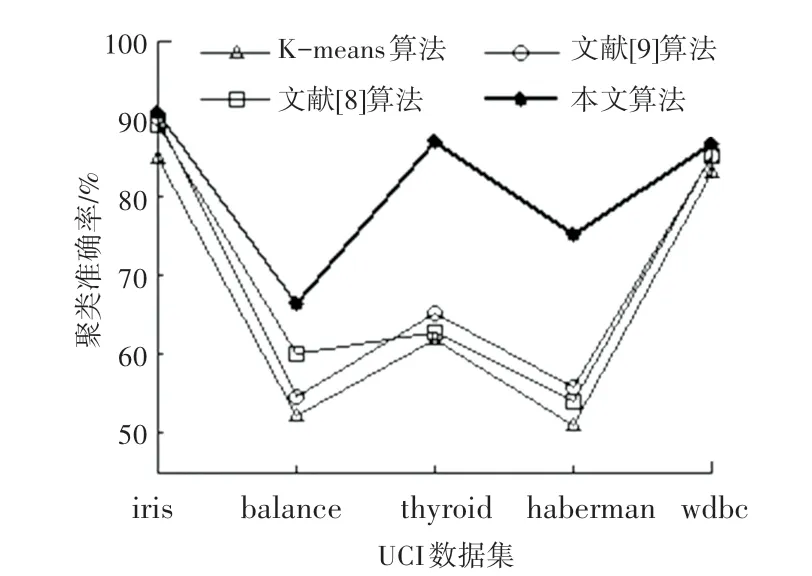
图1 聚类准确率Fig.1 Clustering accuracy

图2 可知，K－means 的初始中心从样本集中随机选择，耗时较少，而文献［8－9］对初始聚类中心的选择过程进行了优化，一定程度上增加了计算开销，故耗时相对较多。与文献［8－9］相比，本文算法先对各样本的密度进行计算，再对高密度代表点进行了二次筛选，以确定初始聚类中心集合。因此，在计算量方面开销较大。除thyroid 数据集的耗时低于文献［9］外，其他数据集上的耗时均略高于文献［8－9］。

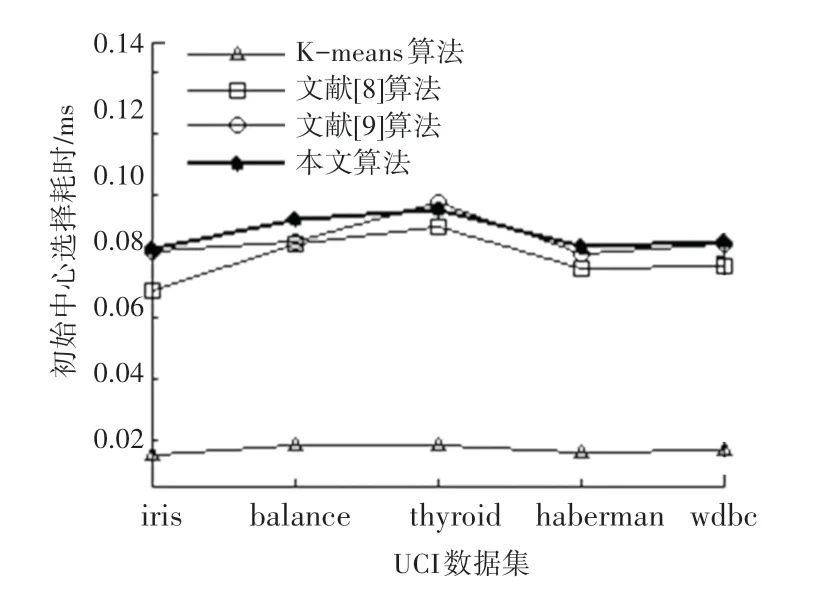
图2 初始中心选择耗时Fig.2 Initial center selection time

从图3 可见，本文算法的簇中心更新耗时小于K－means 和文献［8－9］算法。主要原因在于本文算法将与簇内均值距离最近的样本点作为该簇的临时中心，使得簇中心的存在更加具体。每一次更新后，簇中心的位置和样本的分布情况会愈加明了，簇中心的代表性得到增强，从而降低了簇更新耗时。

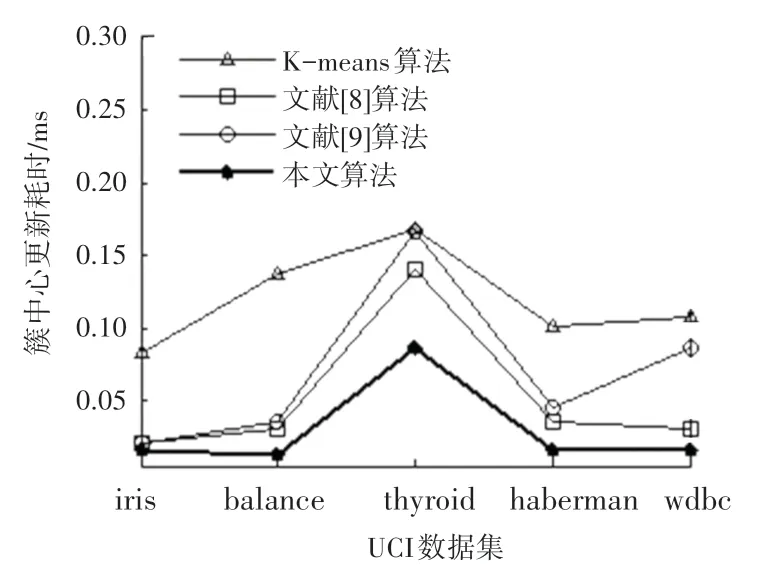
图3 簇中心更新耗时Fig.3 Cluster center update time consuming

从图4、图5 可知，本文算法在中心点迭代次数、总耗时上总体上优于K－means 算法和文献［8－9］算法。这是因为K－means 算法随机选择了初始聚类中心，使得准则函数容易收敛到局部最优，且簇更新次数不稳定。此外，文献［8－9］依然沿用均值中心算法完成簇更新，并未对该阶段进行优化，未能更好地体现临时中心点在当前簇中的代表性。

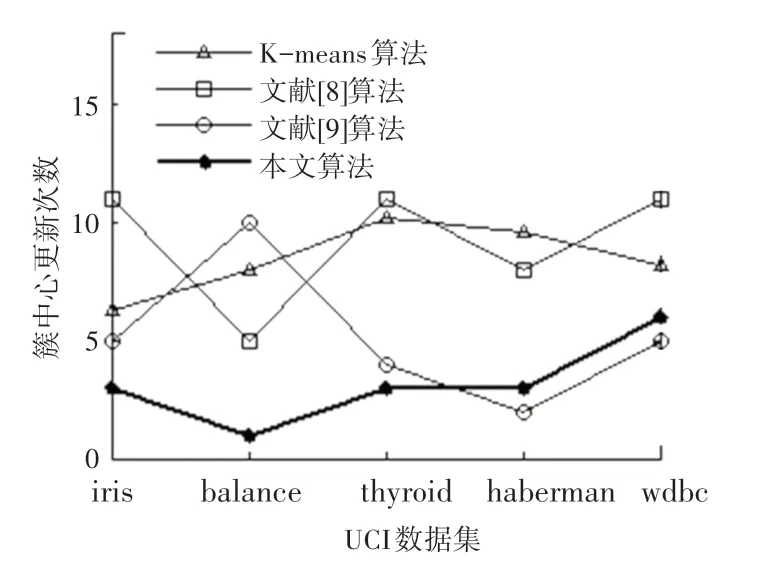
图4 簇中心更新次数Fig.4 Number of cluster center updates

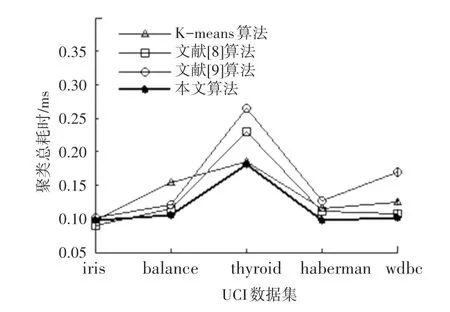
图5 聚类总耗时Fig.5 Total clustering time

综上，本文在初始中心选择阶段所提出的密度计算方法，使得初始中心空间分布合理，具有较强的代表性。簇更新后，簇中心的存在清晰明了，在整体上能够减少簇更新次数，降低运算耗时。

3.2 其它外部评价指标对比

在聚类结果评价方面，除使用上述常用指标外，还使用Rand、Jaccard、Adjusted Rand Index 3 个评价指标［14－17］对5 种样本的聚类结果加以测试对比。观察表2～表4，在Rand 指数对比结果中，除Balance 数据集本文算法略低于文献［8］算法外，其它4 个数据集的Rand 指数均优于其它3 种算法；在Jaccard 系数和Adjusted Rand Index 参数对比结果中，本文算法全部优于其它3 种算法。从几种常见聚类指标对比实验结果中可以看出：本文提出的改进聚类算法稳定性更强，聚类质量更高。

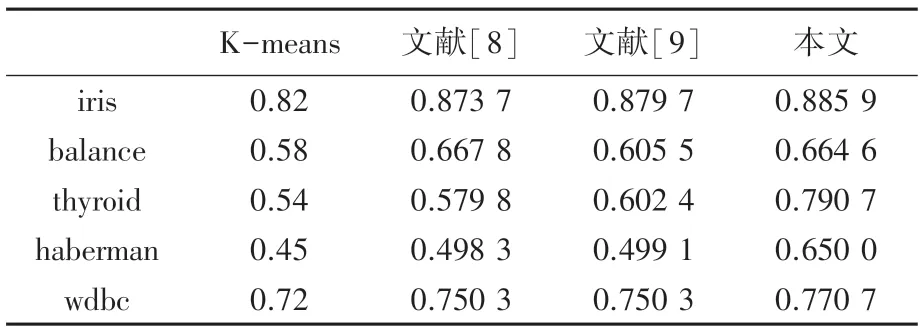
表2 Rand 指数比较Tab.2 Comparison of rand index

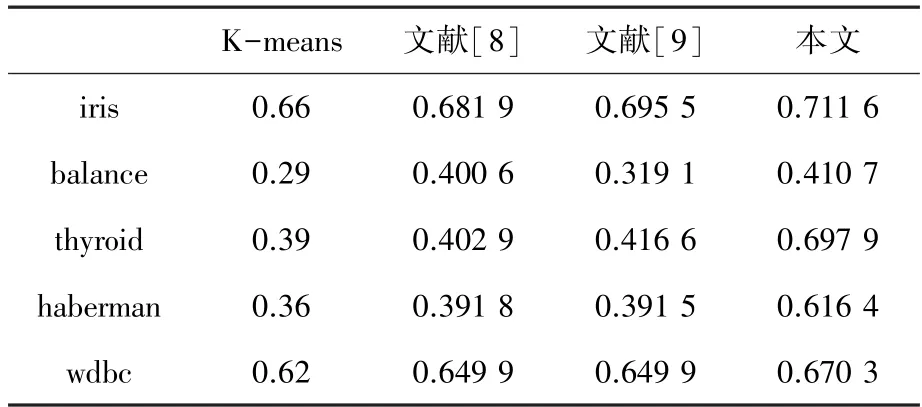
表3 Jaccard 系数比较Tab.3 Comparison of Jaccard coefficient

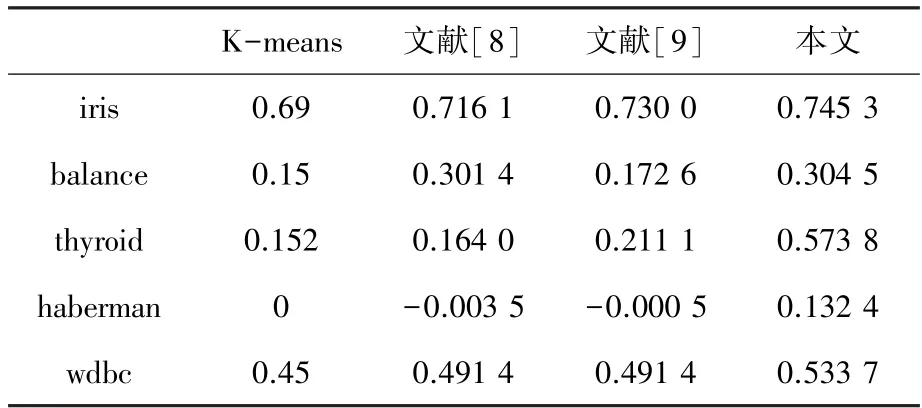
表4 Adjusted Rand Index 参数比较Tab.4 Comparison of Adjusted Rand index parameter

4 结束语

本文用改进密度算法对K－means 聚类算法进行了优化，解决了密度聚类算法的参数设置敏感、收敛时间长等问题。新算法的初始聚类中心相对分散且具有代表性，能够在聚类初期反映出样本的大致分布；在簇更新阶段，选取了与簇内均值距离最近的样本点作为该簇的临时中心，使得簇中心的位置更加准确，减少了迭代次数和计算开销。对比测试表明，新算法能够快速准确逼近全局最优解。