基于樽海鞘群算法的仿生智能孤岛检测新方法

赵倩，胡丹丹，许昊，李忠良，崔立闯

（1.国网河南省电力公司焦作供电公司，河南 焦作 454000；2.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

分布式光伏发电迅速发展的同时也带来了诸多新的问题，其中关键问题之一就是如何检测孤岛效应。孤岛效应是指由于电气故障或自然因素等原因电网中断供电，而光伏并网发电系统并未检测出故障而继续为周围负载供电，从而形成脱离电网公司控制的自给供电系统[1]。这一现象可能会带来损坏用电设备、威胁检修人员人身安全、重合闸失败等严重后果。因此对检测孤岛效应方法的研究具有重要的意义。

孤岛检测方法通常采用本地检测法[2]，其包括主动法和被动法[3-5]。主动检测法通过向电网注入干扰信号，利用扰动信号使电气量发生变化来判断孤岛的发生，主要包括滑模频率漂移法[6]、主动移频法[7]、有功电流扰动法等方法[8-9]，此类方法有效地减小了检测盲区，但对电能质量造成影响[10-12]。被动法主要注重逆变器的输出参数，无需注入扰动量，不会影响电能质量和系统稳定性，但其检测盲区较大，可靠稳定性较差[13-15]。为了避免上述方法的缺陷，文献[16]提出基于MPPT（maximum power point）的无源检测法，相比于传统检测方法，不会引入谐波，且不需要添加其他的设备，但其扰动参数设计不合理，存在检测盲区。文献[17-18]进一步改进了基于MPPT的孤岛检测方法，虽然考虑了最恶劣条件，从而避免检测盲区，但仅仅局限在均匀光照的环境，并未考虑光伏系统常常因环境突变而工作在不均匀光照的工况。

针对现有孤岛检测方法的缺陷，本文提出一种应用于环境突变的基于樽海鞘群算法（salp swarm algorithm，SSA）的MPPT的仿生智能孤岛检测新方法。该方法采用改进的SSA实时跟踪MPP，并利用扰动参数进行周期性地扰动，间接地改变逆变器的输出功率与负载的匹配程度，从而进行孤岛检测。通过仿真验证了所提方法的有效性及可靠性。

1 基于MPPT的孤岛检测方法原理

此类方法的基本原理如下：通过周期性地调节DC/DC换流器的占空比D，间接扰动逆变器输出与负载功率的匹配程度，从而利用过/欠压法或过/欠频法检测出孤岛效应。

常用的两级式光伏并网发电系统示意图如图1所示，其中PPV，QPV分别为光伏阵列输出有功功率、无功功率；P，Q分别为逆变器输出有功功率、无功功率；节点a为并网点；S为断路器；Ug为电网电压；ΔP，ΔQ分别为并网点a送入电网的有功功率、无功功率，也可称为功率不匹配度[16]；R，L，C为本地等效负载；PLoad，QLoad分别为负载有功功率、无功功率。忽略逆变器、线路等损耗，光伏输出功率与逆变器输出功率相等，即PPV=P，QPV=Q。

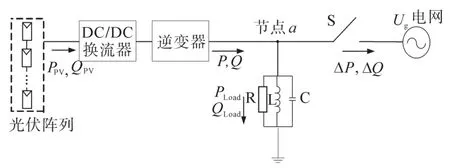
图1 常用两级式光伏并网发电系统Fig.1 Schematic diagram of the two-stage grid-connected PV generation system

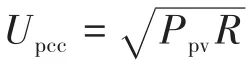
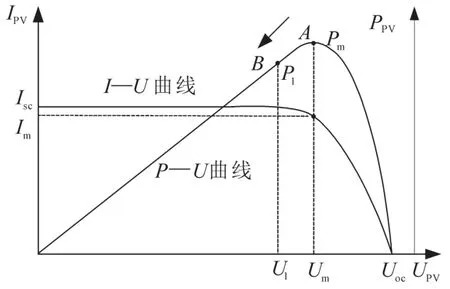
图2 光伏电池板输出特性曲线Fig.2 Output characteristic curves of the photovoltaic array

2 SSA算法的基本原理

SSA算法是由Mirjalili等人在2017年以樽海鞘群体的特征提出的仿生算法[19]。与其他群体不同，樽海鞘并不是以“群”的方式分布，而是呈“链”状分布，其中某个樽海鞘仅对紧挨着自己的樽海鞘产生影响，而不能直接影响其它樽海鞘。这种严格的等级制度使得在群体移动过程中不至于随机地发散移动，且不会一味地朝某一方向移动，导致算法陷入局部最优。

假设在N维的欧式空间，其中N表示群体规模，种群的位置信息可以用二维矩阵表示。领导者负责在空间中搜索食物源，引领整个群体移动，按下式更新位置：

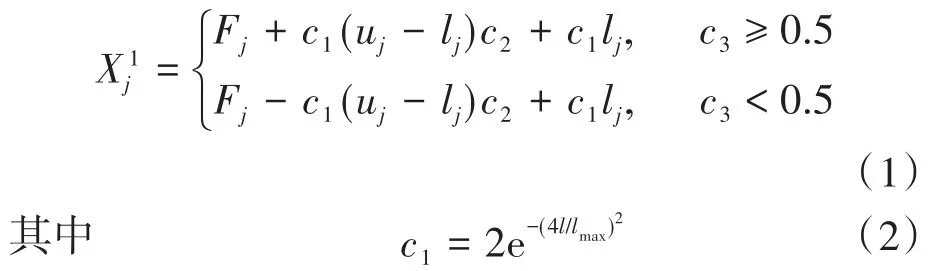
c1常常被称为收敛因子，用于平衡算法在迭代过程中的探索和开发能力。当收敛因子大于1时，算法进行全局探索；当收敛因子小于1时，算法进行局部开发，进而精确地寻找最优值。跟随者成链状依次跟随领导者移动，按下式更新位置：

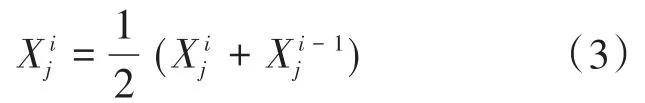
为了加快算法的收敛时间，对原始算法进行优化，在跟随者位置更新时，增加线性减小的惯性权重w，即

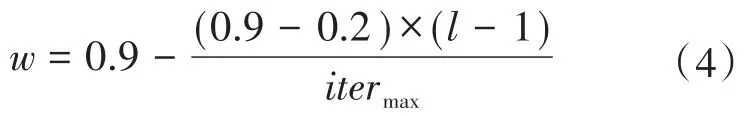
式中：l为当前迭代次数；itermax为最大迭代次数。优化后的跟随者更新公式为

相对于目前的仿生智能算法，SSA具有较快的收敛速度，且仅需更新一个参数。考虑到光伏系统常常工作在变化的环境中，而传统MPPT算法易陷入局部最优，当孤岛发生后需要确保快速有效地检测以及对突变环境的适应，因此本文采用改进SSA算法，从而使所提孤岛检测方法具有更好的适应性。

同时，算法需要实时跟踪MPP，即当光照、温度等外界环境变化时，光伏阵列的输出功率也跟随变化，因此为避免算法陷入死循环，需要重新启动算法进行功率跟踪。当输出功率变化满足下式时，重新启动算法。

式中：Preal为光伏阵列实际的输出功率；Pm为当前工况下光伏阵列在MPP处的输出功率；ΔP为光伏阵列输出功率变化的阈值，设置为0.5。

3 基于SSA的仿生智能孤岛检测方法

IEEE Std.92—2000，UL1741等标准提出分布式供电系统必须具有检测孤岛效应的功能，其要求当发生孤岛效应后并网点电压UPCC1满足0.88UN≤UPCC1≤1.1UN（UN为电网电压额定值）时，允许最大检测孤岛的时间为2 s。

考虑到施加扰动时尽可能小地引起并网点电压波动及功率的损失等因素，所提出的仿生智能孤岛检测新方法采用每隔1 s施加一次扰动，扰动持续时间为2个工频周期，每个工频周期内的扰动量由并网点电压自适应地变化。这样既能够有效地减小孤岛效应的持续时间，又能保证所提方法的可靠性。因此本文所提出的基于SSA的仿生智能孤岛检测新方法的具体过程介绍如下：

1）孤岛效应发生前，由改进的SSA算法实时寻找最大工作点，并维持系统稳定运行，同时实时检测孤岛效应；

2）若孤岛效应发生后，当并网点电压UPCC1的幅值和频率大小满足条件：a）UPCC1＜0.88UN；b）UPCC1＞1.1UN；c）f-fg＞0.5 Hz中的任意一个，即可依据过/欠压检测法或过/欠频检测法确定为孤岛状态，其中，f为并网点电压频率，fg为电网电压频率。

当并网点电压UPCC1满足0.88UN≤UPCC1≤1.1UN，则需要施加一定扰动，使并网点电压降至0.88UN以下，即通过施加扰动改变逆变器输出功率与负载功率的匹配程度，扰动后占空比D1的取值由下式决定：

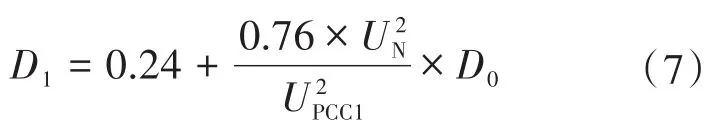
式中：D0为扰动之前的占空比。

由于扰动周期为1 s，每扰动周期持续时间为2个工频周期，故在实际计算时，式（7）中UPCC1取为U50n-2（n为正整数），则D1也可表示为

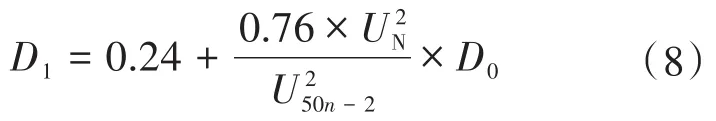
假设光照强度和温度不发生突变的情况下，即施加扰动时外界环境保持恒定，根据Boost升压电路的原理，本文所提方法对逆变器输出功率的影响如下式所示：

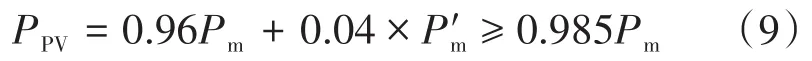
式中：P′m为扰动时光伏阵列的输出功率；系数0.96和0.04分别为一个周期内正常工作时间、扰动时间所占周期的比例。

从式（9）可以看出，所提出的仿生智能孤岛检测方法造成的功率损耗不足1.5%。

上述等式成立的条件是基于光伏阵列P—V曲线为单峰值的结果，当P—V曲线呈多峰值时，可以借鉴文献[20-22]针对处理不均匀光照下光伏阵列P—V曲线所提出的策略。多峰值P—V特性曲线如图3所示。

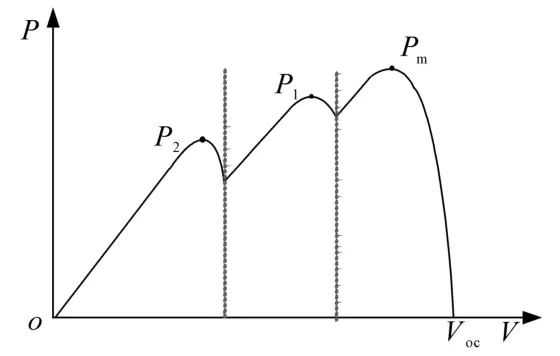
图3 多峰值P—V特性曲线Fig.3 Multi-peak P—V characteristic curve

图3中，虚线将多峰值P—V曲线分为三部分，各部分曲线所对应的峰值点分别为Pm，P1，P2，各部分曲线均可以由一个等效的关键模块所决定[22]，且曲线的左半部分可以近似为线性，即Pi=kUi，（i表示所划分的部分）。因此上述等式仍适用于不均匀光照的条件。

综上所述，当孤岛发生后并网点电压UPCC1在0.88UN≤UPCC1≤1.1UN范围内时，无论P—V曲线是否为单峰值，施加周期性扰动，可以将并网点电压幅值降到0.88UN以下，超出了过/欠压保护阈值，从而判断出孤岛效应，避免检测盲区。所提方法流程图如图4所示。

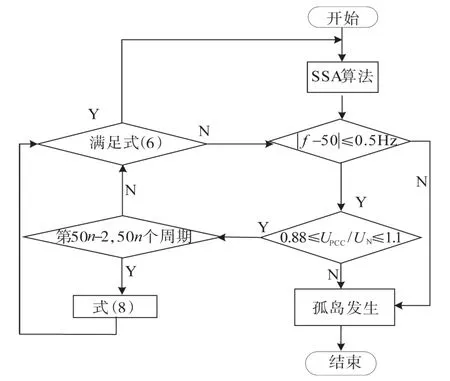
图4 所提方法的流程图Fig.4 Flow chart of the proposed method

4 仿真验证

为了验证所提新方法的有效性及可靠稳定性，在Matlab/Simulink中搭建如图1所示的光伏发电并网系统仿真模型。DC/DC，DC/AC换流器分别采用Boost升压电路、三相全桥逆变电路。三个光伏阵列构成的光伏系统参数设置为：额定输出有功功率400 kW；电网相电压峰值311 V；电网阻抗Lg=0.05 mH；电网频率50 Hz；直流母线电压700 V。滤波电路的参数为：逆变器侧滤波电感Li=0.11 mH，滤波电容Cf=137 μF，网侧滤波电感Ls=0.022 mH；开关频率fs=10 kHz。

仿真光照条件分别为光照强度为1 000 W/m2的均匀光照及光照强度为1 000 W/m2，800 W/m2，600 W/m2的不均匀光照；本地负载分别为R=Rm即UPCC1=1.1UN（Rm为逆变器输出有功功率与负载有功功率平衡时的负载电阻），R=1.21Rm即UPCC1=1.1UN。

采用IEEE Std.92—2000规定推荐的RLC负载谐振频率为50 Hz、品质因数Qf=2.5。本文所提出的孤岛检测方法，扰动周期为1 s，每个周期对MPPT实施连续的2个工频周期扰动。设置0.7 s时发生孤岛效应。因在三相平衡条件下，三相电压、电流波 形相同，相位相差120°，故本文仿真只给出a相电压、电流波形。

当UPCC1=UN即R=Rm情况下，在光照强度为1 000 W/m2的均匀光照条件下，正常工作时扰动前后波形如图5所示，其从上至下分别为光伏阵列输出功率PPV、占空比D、光伏阵列输出电压UPV、直流母线电压Ubus、并网点a相电压UPCCa和a相电流IPCCa曲线。改进的SSA算法在0.14 s寻找到MPP并稳定运行。当仿真时间到达0.96 s时通过改变占空比D施加扰动，此时光伏阵列的输出电压UPV、输出功率PPV均减小。虽然并网点a的电压UPCCa受电网电压的钳位，但由于电网阻抗的存在，其仍发生轻微的波动，逆变器输出的a相电流IPCCa减小。上述的参数变化波形均与理论分析相符合，验证了所提方法的有效性。

在光照强度为1 000 W/m2的均匀光照条件下发生孤岛效应后，其扰动前后波形如图6所示。仿真中设置为0.7 s时光伏并网系统脱离电网，即发生孤岛效应，当检测到孤岛效应后，立即关断逆变器桥臂功率开关管。由于逆变器输出有功功率与负载有功功率平衡，即R=Rm，从图6b、图6c可以看出，并网点电压UPCC1幅值没有发生突变，此时系统处于孤岛运行且并网点电压、频率都在正常范围内。从图6a可以看出在0.96 s对占空比D进行扰动，此时，光伏阵列的输出电压UPV、输出功率PPV减小，导致a点电压UPCCa，a点功率PPCCa生波动，且电压幅值减小到0.88UN以下，从而检测出孤岛效应，该方法的检测时间约为20 ms。

图5 均匀光照下正常扰动波形Fig.5 Normal disturbance waveforms under uniform irradiation

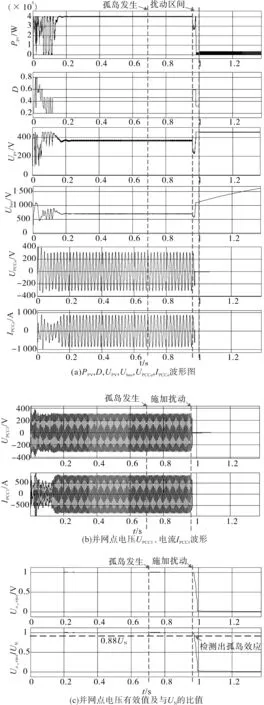
图6 均匀光照且孤岛状态下扰动波形图Fig.6 Disturbance waveforms under uniform irradiation and island state

不均匀光照的仿真采用三组光伏组件，光照强度分别为 1 000 W/m2，800 W/m2，600 W/m2，其光伏阵列的P—V特性曲线如图7所示。由图7可知，最大输出功率Pmax为275.1 kW。当不均匀光照条件下发生孤岛效应时，若逆变器输出功率与负载功率不平衡时，则可由欠/过压法直接检测出孤岛效应，波形图如图8所示，其负载功率设置为400 kW。

因此，本文假设不均匀光照时逆变器输出功率与负载功率平衡，即R=Rm。此时并网点电压UPCC1幅值没有发生突变，系统处于孤岛运行且并网点电压、频率都在正常范围内，其扰动前后波形如图9所示。从图9a可以看出：在不均匀光照下改进的SSA算法能够在0.138 s寻找到MPP并能稳定运行，稳定时的输出功率为273.8 kW，SSA算法的跟踪效率为99.52%，证明了改进的SSA算法在不均匀光照下的有效性。在0.96 s时施加扰动，经过约为一个工频周期，检测出孤岛效应，逆变器将停止工作，光伏阵列处于开路状态，输出功率减小至零，从图9可以看出参数波形变化和理论分析相符，验证了方法的有效性，同时证明了第3节假设的成立。从图9c可以看出，所提方法能够在20 ms检测出孤岛效应。

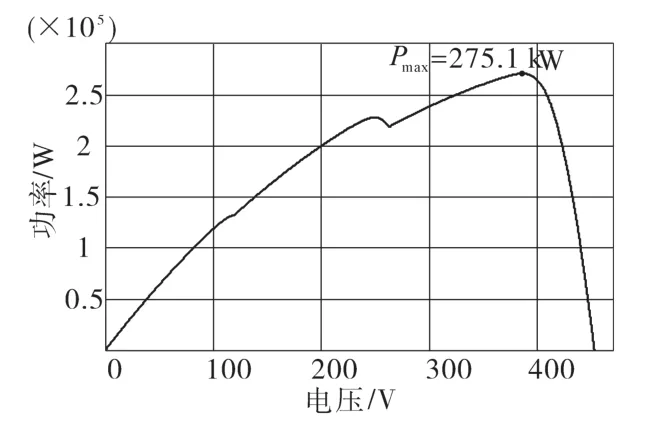
图7 不均匀光照下P—V特性曲线Fig.7 P—V characteristic curve under partial shading conditions

图8 功率不匹配时孤岛状态下扰动前后的波形Fig.8 Waveforms before and after disturbance under island state when power mismatch

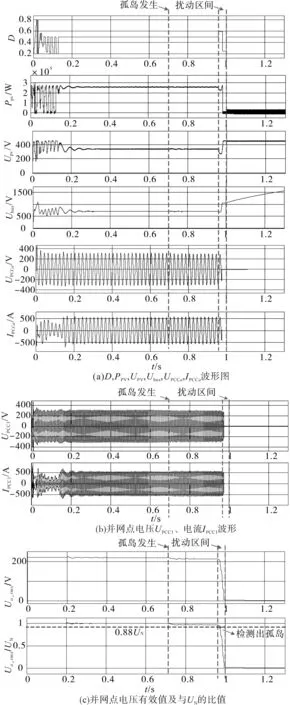
图9 不均匀光照且孤岛状态下扰动前后的波形Fig.9 Waveforms before and after disturbance under partial shading conditions and island state

为了充分证明基于改进的SSA算法的孤岛检测方法在不均匀光照下的稳定性及有效性，采用基于传统扰动观察法（P&O）的孤岛检测方法进行仿真对比，如图10所示。从图10a可以看出算法能够在0.14 s跟踪到“最大功率点”，光伏阵列输出功率稳定在230 kW，P&O算法的跟踪效率为83.64%，且纹波较大，与改进SSA算法的99.52%相差较大。在t=0.7 s时发生孤岛效应，t=0.96 s施加扰动，当施加扰动后即占空比增大，光伏阵列的输出电压减小、输出功率略微增大，说明其稳定时陷入局部最优值；并网点电压发生微小的波动其并网点电压幅值并未超出0.88UN≤UPCC1≤1.1UN，即扰动后仍无法检测出孤岛效应。因此，基于P&O算法的孤岛检测方法并未有效地检测出孤岛效应。

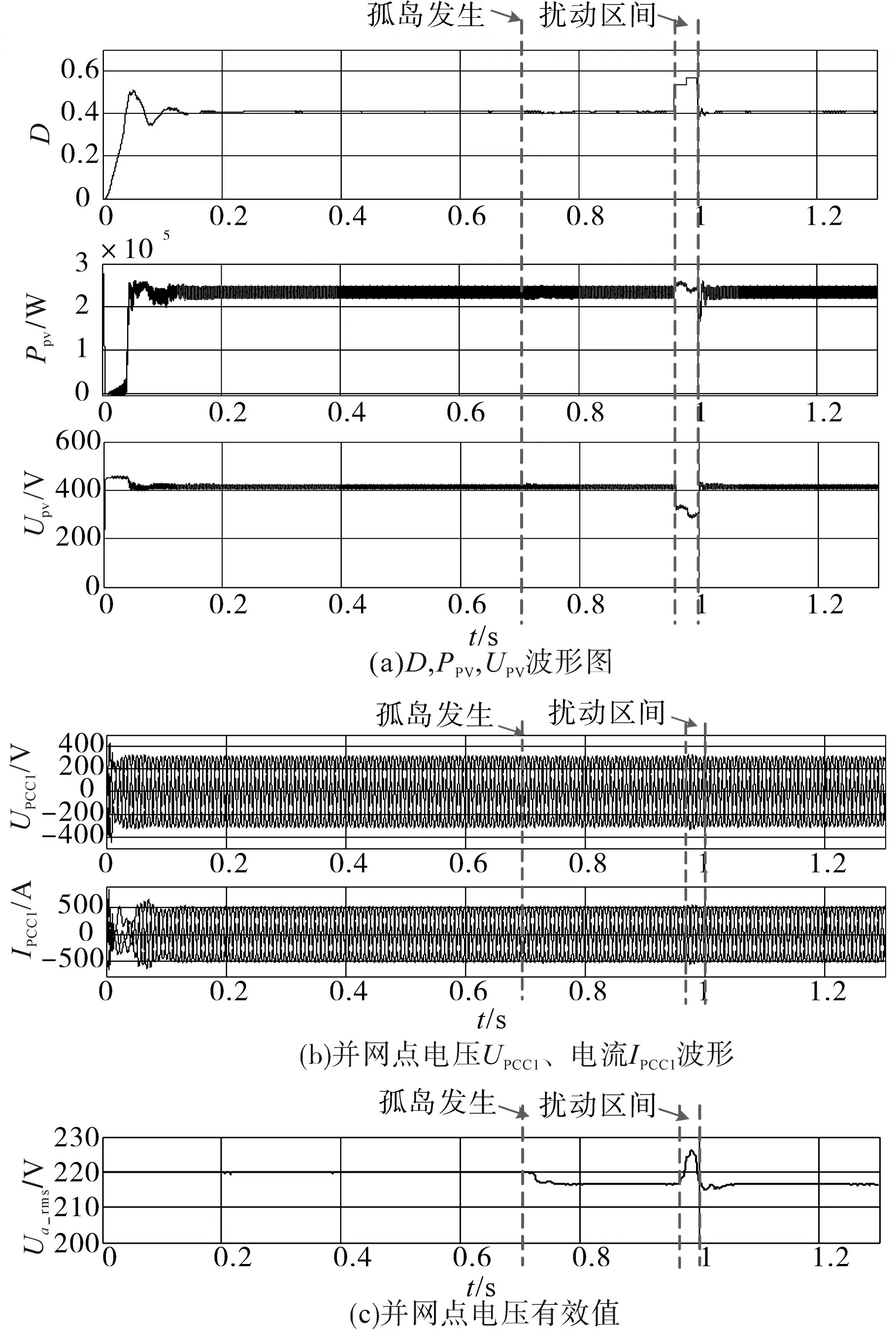
图10 基于P&O的孤岛检测方法Fig.10 The island detection method based on the P&O MPPT algorithm

考虑到所提方法在最难检测的工况的适应性，即 UPCC1=1.1UN，R=1.21Rm，本文给出不均匀光照且UPCC1=1.1UN时，孤岛状态下扰动前后的仿真结果，如图11所示，进一步说明所提方法的有效性。

由图11可知，图11a、图11b所示的波形图符合上述理论分析，从图11c可以看出，由于R=1.21Rm，当0.7 s发生孤岛时，其并网点电压UPCC1近似升到1.1UN，当0.96 s时施加一定的扰动，使得并网点电压UPCC1降低至0.88UN以下，从而检测出孤岛效应。

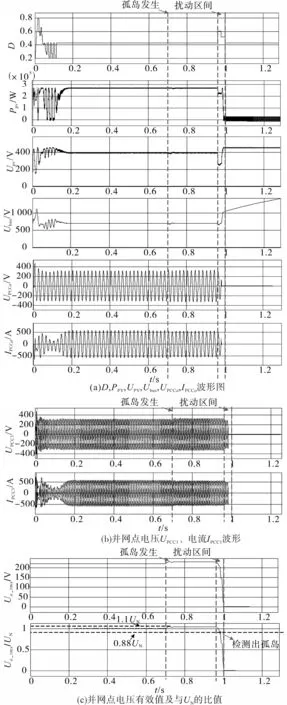
图11 不均匀光照下UPCC1=1.1UN且孤岛状态下扰动前后的波形Fig.11 Waveforms before and after disturbance under partial shading conditions and island state

5 结论

本文提出了基于SSA的仿生智能孤岛检测新方法。当逆变器输出功率与负载功率相匹配时，所提方法根据扰动前并网点的电压U50n-2确定所需扰动占空比D的大小，间接改变逆变器输出功率，通过判断扰动后并网点电压是否低于0.88UN从而判断是否发生孤岛效应；当逆变器输出功率与负载功率不匹配时，所提方法通过欠/过压检测判断是否发生孤岛效应。MPPT采用SSA算法进行实时跟踪MPP，使得该方法能更好地适应环境的变化。根据IEEE Std.92—2000规定并考虑最恶劣环境，进行均匀光照、不均匀光照下的仿真验证，仿真结果表明了所提新方法的稳定性及有效性，且无检测盲区。