高精度定位系统的摩擦力自适应前馈补偿

（清远职业技术学院机电与汽车工程学院，广东 清远 511510）

高精度定位系统广泛应用于航空航天、军工打印机、医疗器械及IC装备等领域，定位系统的精度和响应速度等指标直接影响军用设备的加工精度及医疗器械的治疗效果等，因此研究有效提高定位系统的精度对国防军工、医疗卫生和生产生活的各领域有着重要意义。随着工业控制对高精度定位系统要求不断提高，提升定位系统精度和响应速度是目前学术研究的重点和热点[1-4]。

定位系统在运动控制过程中的精度与系统的机械精度、传感器分辨率、电机本体特性及控制器算法密切相关，其中良好的控制器算法能够有效抑制系统外部干扰、补偿机械平台的非线性摩擦等，提高系统定位精度。对于利用机械传动实现的高精度定位系统，在运行过程中不可避免存在静摩擦力和库伦摩擦力，二者是影响系统定位精度的重要因素。为此，国内外学者对抑制摩擦力提高系统响应速度和定位精度进行大量研究，目前对于系统摩擦力补偿主要分为两类，一类是基于摩擦力模型的补偿方法，一类是设计合理的控制策略或观测器实现对摩擦力的无模型补偿。

马立[5]等学者提出基于Stribeck摩擦力模型的建模和补偿方法，利用最小二乘法确定Stribeck模型的待定参数，通过二维精密定位平台低速运动验证了建模和补偿方法的有效性。王鹏[6]等学者对传统Lugre模型进行修正，并利用遗传算法实现Lugre模型的参数辨识，根据液压缸平台验证其摩擦力实验结果与辨识结果的一致性。孟凡淦[7]等学者针对气动伺服系统，提出了基于遗传算法的Lugre模型参数辨识方法，通过气缸高精度轨迹跟踪控制实验验证了所提方法的可行性。上述方法是基于摩擦力模型的辨识和补偿策略，需要通过辨识方法确定摩擦力数学模型和参数，对系统模型和参数辨识的准确性要求较高，且由于不同系统摩擦力模型特征有所差异，此种方法未能够在工业控制领域取得广泛应用。

余敏[8]等学者针对直流伺服系统未知死区和摩擦力参数问题，提出一种鲁棒自适应控制补偿方法，利用Lyapunov证明控制器稳定性的基础上，通过仿真验证了算法在补偿摩擦力和死区方面的作用。马丙华[9]为优化光电稳定平台的动态响应性能和扰动抑制性能，提出基于迭代学习控制的扰动补偿和位置环跟踪控制，利用迭代学习补偿系统运动控制过程中的周期性干扰和误差，以提高平台的动态响应和抗扰动性能。Farrage[10]等学者针对数控精密机电控制平台，利用滑模控制算法和扰动观测器补偿机械系统存在的静摩擦力，通过实验验证了所提方法对系统位置跟踪精度和系统响应能力的提高。由此可见，基于控制策略和观测器的补偿策略可以在系统运行过程确定摩擦力等扰动的补偿量，通过前馈补偿方式提高定位系统控制性能。

为了扩展控制方法的普适性，使其广泛应用于不同工况条件，本文提出一种基于自适应的摩擦力前馈补偿方法，首先建立被控对象的数学模型，其次根据模型特点设计自适应控制环节，并验证所提控制方法的稳定性，最后通过仿真和高精度定位平台试验验证所提方法对摩擦力等干扰的前馈补偿效果。

1 高精度定位系统数学模型

本文所述高精度定位系统主要由机械平台、直驱电机、驱动器和控制器组成，针对机械平台和驱动环节，忽略电机电感和推力波动等非线性环节，可建立数学模型如图1所示，其表达式为

其中

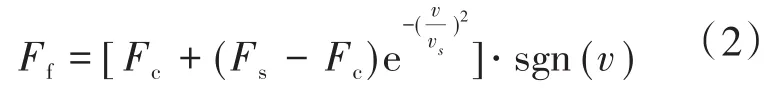
式中：F为直驱电机施加到机械平台的推力；Kt为直驱电机的推力系数；i为加载到直驱电机的输入电流，其为随时间变化的控制量；m为机械平台的等效质量；B为机械平台在运动过程中的阻尼系数；v为机械平台在直驱电机作用下的运动速度；Ff为机械平台运动过程中的摩擦力；Fc为库伦摩擦力；Fs为最大静摩擦力；vs为Stribeck摩擦速度；sgn（·）为符号函数。

式（2）为Stribeck摩擦力模型。

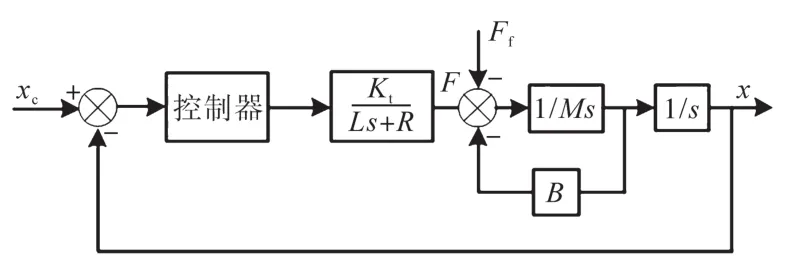
图1 高精度定位系统数学模型Fig.1 Mathematical model of high precision positioning system

为有效抑制系统定位运动过程中摩擦力对其精度和响应的影响，将摩擦力视为系统扰动，并利用自适应控制策略实现在线补偿，以提高系统动态特性。为此，根据式（1）建立如下参考模型作为模型参考自适应控制的基准。

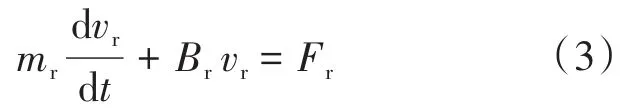
式中：带有下标“r”的为所建立的参考模型。

根据系统数学模型确定其物理参数，在此基础上引入参考模型进行在线实时比较，并利用合理的控制策略实现模型自适应控制。

2 自适应控制策略

图2为基于自适应摩擦力前馈补偿的控制原理框图。由于被控对象直驱电机数学模型已知，机械平台及粘滞摩擦系数未知，基于自适应控制原理将系统分为基于参考模型的变换控制回路和基于被控对象的闭环控制回路，将被控对象与参考模型的控制量输入、位置输出以及参考模型与被控对象输出误差作为自适应控制率的输入，设计合理的自适应控制率，实现外部干扰（摩擦力及传感器噪声等）引起的跟踪误差。基于自适应控制策略的目标，即将实际被控对象等效为理论参考模型，由于自适应控制率作用于系统控制器外部，利用有效的输入信息，补偿实际被控对象的外部干扰。

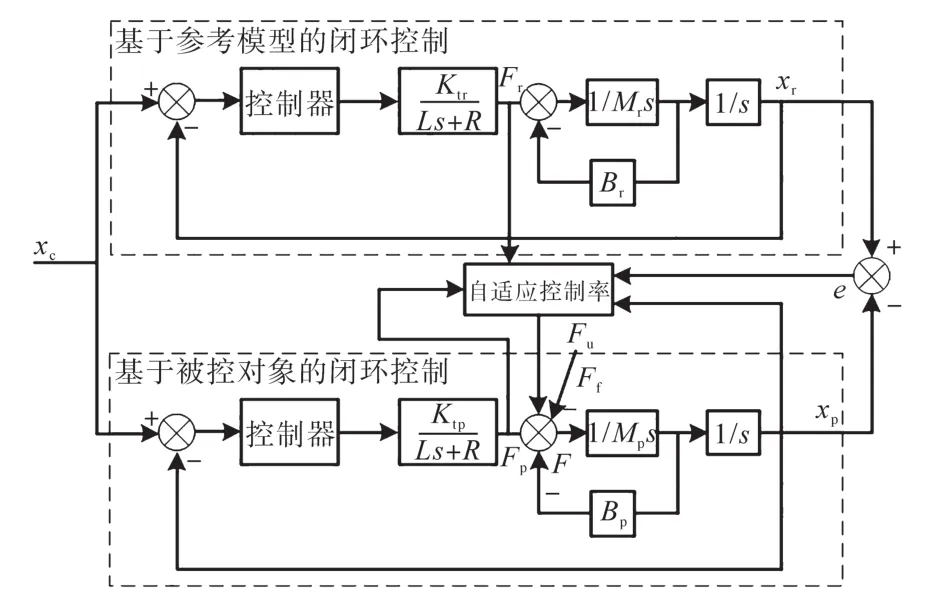
图2 基于自适应摩擦力前馈补偿的控制原理框图Fig.2 Control principle block diagram based on adaptive friction feedforward compensation

参考模型位置输出与被控对象位置输出的误差及其一阶导数定义如下：

式中：e为参考模型的位置输出与被控对象的位置输出的误差，即基于参考模型的估计输出与实际输出的误差值。

由于此误差为时间的动态参数，因此其随时间的一阶导数即上述二者速度的变化量。对于被控对象，包含控制器和自适应控制率的控制输入定义如式下：

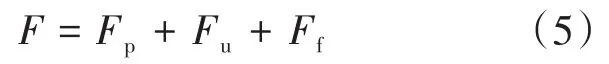
式中：Ff为系统摩擦力干扰输入；Fp为被控对象的控制输入；Fu为利用自适应控制率计算所得的控制量输入。

Fp主要基于被控对象数学模型计算控制量，Fu的自适应控制输入主要抑制未知干扰对系统精度的影响。

将式（1）～式（3）和式（5）代入式（4），可得到：

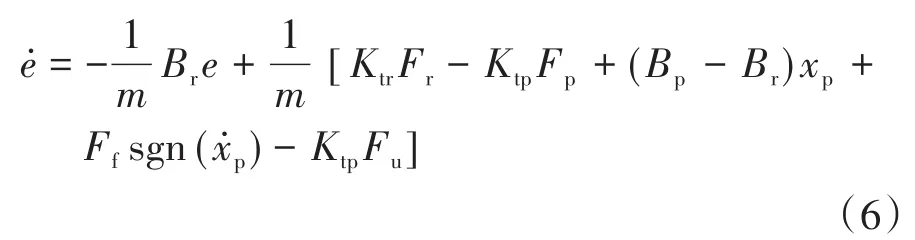
式中：Fr为参考模型的控制量输入；Ktr为基于参考模型的闭环控制回路中的电机转矩系数；Ktp为被控对象的闭环控制回路中的电机转矩系数；Bp为基于参考模型的闭环控制回路中粘滞摩擦系数；Br为被控对象的闭环控制回路中的粘滞摩擦系数。根据式（6）计算可知，当式（6）的Fu满足下式中的数学关系：

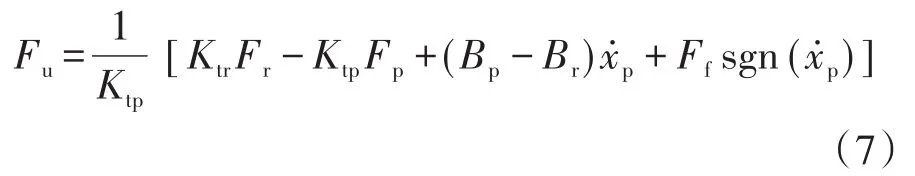
式（6）可以简化为

根据微分方程解的形式可知，上述微分方程中e具有衰减形式的解。即当自变量t随时间变化为无穷大时，满足如下关系：

由此可见，设计如下自适应控制率：

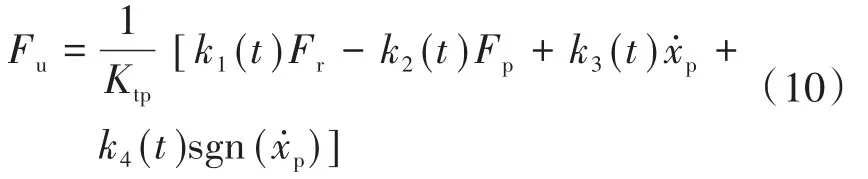
式中：k1（t），k2（t），k3（t）和k4（t）为自适应控制率中的待定系数，要根据系统稳定性分析确定。

这样设计可以使得实际被控对象位置输出与参考模型位置输出实现跟随效应，即实现被控对象在含有未知扰动过程中的模型等效，利用自适应控制率消除系统未知干扰的作用。

3 控制策略稳定性分析

针对式（10）形式的自适应控制率，利用Lyapunov函数证明控制率在控制过程中的稳定性，并确定其中的待定参数表达形式。将式（10）代入式（6）中可以得到：

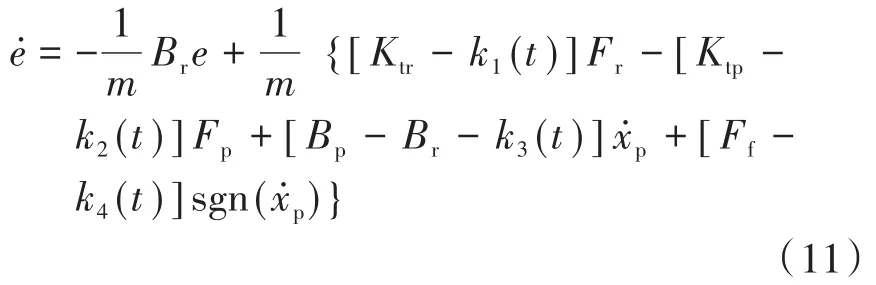
为便于系统参数矩阵化表示，定义参数如下：

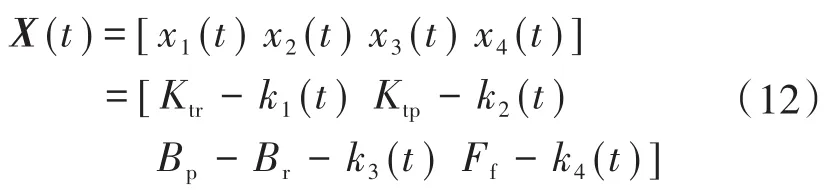
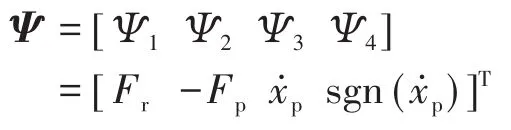
根据所定义的参数，式（11）可以表达为

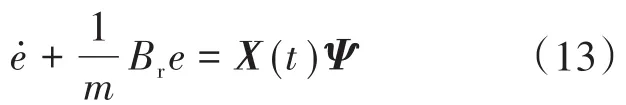
根据式（12）～式（13）可知，参数Ψ在系统运行过程中为已知信息，可以根据控制器计算输出和反馈位置及速度信息获取。因此，为对自适应控制率进行稳定性分析，根据经典“比例-积分”参数更新率设计[11]，定义Lyapunov函数：

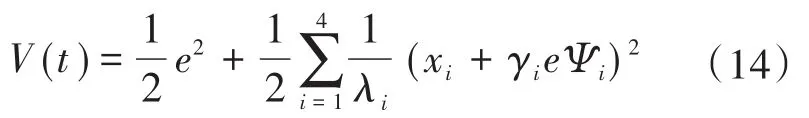
由于系统中的质量、电机转矩系数及粘滞摩擦系数等为慢时变参数，对式（14）两边求导可得：

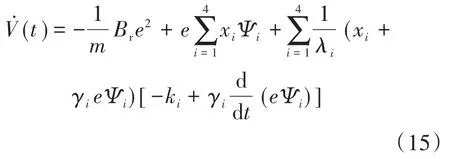
根据式（15）确定自适应控制率中的参数为

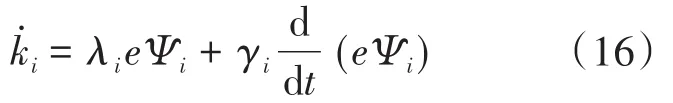
可以有：

对式（16）积分运算，有：

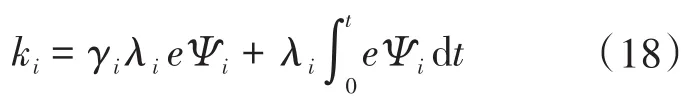
针对被控对象调节控制器参数时，需要根据不同的位置指令形式确定其中的λi和γi，以保证控制过程中最优的动态系统响应。

4 试验验证

为了验证本文所提的基于自适应前馈补偿控制器的正确性，利用典型单轴直驱工控平台对上述算法验证分析。试验平台由机械导轨滑块、松下400 W直驱伺服电机、1 μm分辨率的雷尼绍光栅尺及自主研发的基于TMS320F28335的DSP控制器组成，利用控制器输出电压信号作为直驱伺服电机的输入信号，通过实时采集并处理光栅尺传感器的位置信号实现反馈控制，在控制器中实现本文所述算法的验证。图3为系统结构图，根据位置指令输入和光栅位置反馈信息，在驱动器为模拟量电压控制模式下，控制器实时计算电压控制指令，实现机电系统的闭环反馈控制。

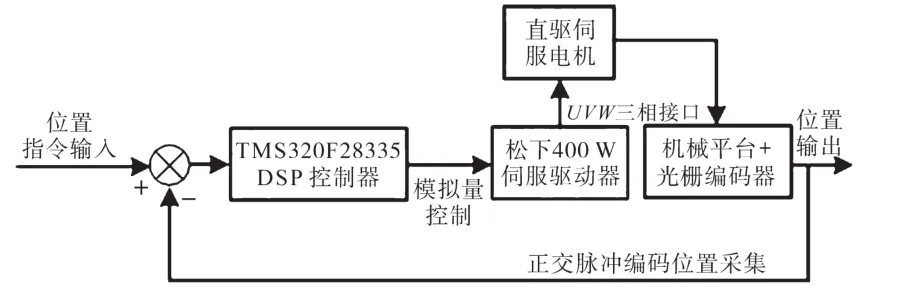
图3 系统结构图Fig.3 Schematic introduction of the system

为了充分验证所提算法的普适性，首先验证在正弦位置指令输入状态下控制器的跟踪响应特性，通过对比传统控制器与含有自适应摩擦前馈补偿控制器的跟踪误差，对比说明算法对控制性能的影响。正弦位置指令幅值为10 mm，周期为1 s，控制器对光栅尺位置采样周期为100 μs，图4为不同控制方法对正弦指令的跟踪结果。

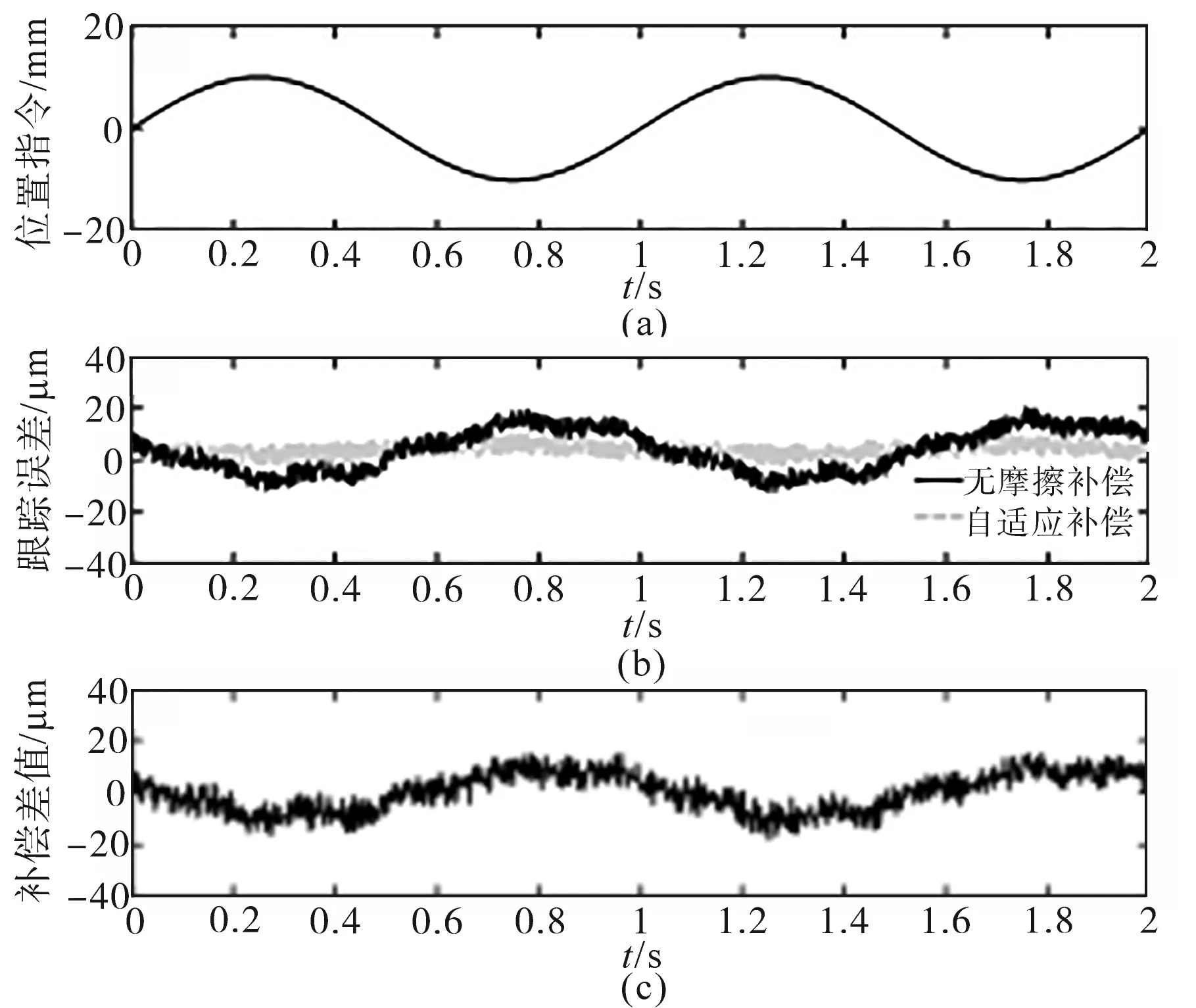
图4 摩擦力自适应前馈补偿控制器对正弦指令跟踪Fig.4 Tracking sinusoidal instructions by friction adaptive feedforward compensation controller

图4a为指令位置轨迹，图4b为两种控制方法下的跟踪误差，其中无摩擦补偿时的跟踪误差的最大值为21.2 μm、均方根值为9.1 μm；基于自适应摩擦补偿时的跟踪误差的最大值为9.9 μm、均方根值为4.8 μm。图4c为基于自适应摩擦补偿控制策略的跟踪误差与无摩擦补偿时跟踪误差的差值对比，其反映了利用自适应摩擦补偿方法对系统动态响应特性提升的作用。综上所述，基于自适应的摩擦力前馈补偿方法能够有效抑制摩擦力等系统外部扰动对系统动态性能的影响。

为了说明所提方法与传统自适应控制策略的差异，本文对传统模型参考自适应[11]和基于自适应摩擦补偿的控制方法进行试验对比分析，两者动态响应特性如图5所示。

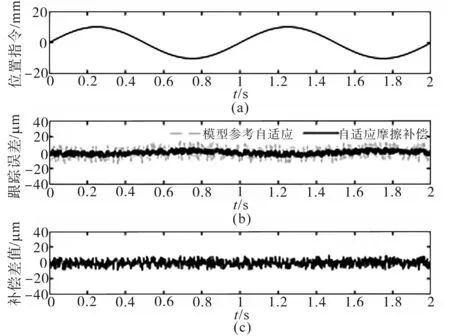
图5 不同自适应控制策略动态性能分析Fig.5 Dynamic performance analysis of different adaptive control strategies

利用两种控制方法跟踪图5a的正弦指令，图5b为两种方法跟踪误差，其中基于模型参考自适应方法的跟踪误差均方根值为5.6 μm，基于自适应摩擦补偿控制方法的跟踪误差均方根值为4.6 μm，图5c为两种控制方法跟踪误差的差值对比，其反映两种控制方法对系统动态特性提升的影响。由于模型参考自适应控制策略针对系统未知干扰进行补偿，而自适应摩擦补偿主要针对式（2）的Stribeck摩擦力进行补偿，因此根据图5b可知，普适性较强的模型参考自适应控制策略能够在一定程度补偿系统摩擦力干扰，而基于摩擦力补偿的自适应控制策略能够更好地补偿系统摩擦力干扰。

针对无摩擦补偿、基于模型参考自适应及基于自适应摩擦补偿三种控制策略的位置跟踪试验，在系统运行过程中分别监控其电压指令，即图3中的模拟量控制信号，电压指令监控试验结果如图6所示。对比分析可知，基于自适应摩擦补偿的控制方法能够快速跟踪位置指令，准确补偿摩擦力干扰；基于模型参考自适应的控制方法也可实现有效补偿，但其与自适应摩擦补偿控制方法的电压指令有迟滞，即控制器对摩擦力干扰的补偿响应速度较慢；而无摩擦补偿的PID控制算法没有对摩擦力干扰进行针对性补偿，电压指令变化慢，动态响应精度差。综上所述，基于自适应摩擦补偿的控制方法能够较好地补偿摩擦力引起的系统动态误差。

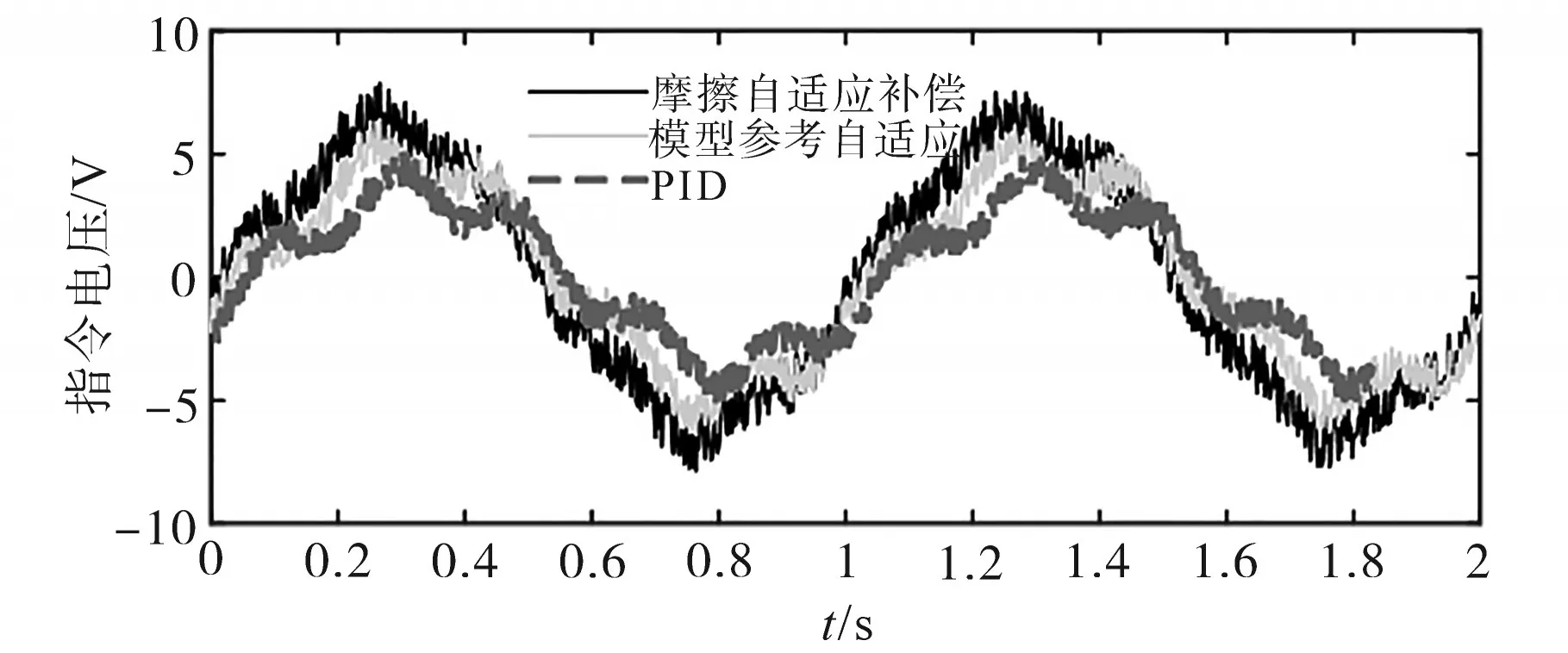
图6 不同控制策略指令电压对比Fig.6 Voltage command of different control strategies

5 结论

为了提高高精度定位系统的动态响应和跟踪能力，提出了基于自适应前馈的摩擦力补偿方法，根据系统数学模型，设计合理的自适应控制率，并利用Lyapunov函数证明了控制方法的稳定性，并给出了具体的自适应控制率数学表达。通过试验对本文所提方法进行验证，在跟踪正弦指令轨迹时，基于自适应前馈补偿的方法能够有效抑制外部扰动对系统动态性能的影响，有效提高了系统控制精度，证明了所提方法的有效性。