铰接式转向架构架疲劳强度算法优化研究
2021-02-28
(北京轨道交通技术装备集团有限公司,北京 100071)
1 研究背景
车辆转向架的构架疲劳强度分析是转向架构架设计的关键环节,对转向架运用过程的安全性有重大影响[1-2],国内外也有很多与之相关的标准和研究[3-6]。DVS 1612为德国《铁路车辆结构钢焊接接头设计和疲劳强度评估》标准,其中对转向架构架常用的焊接接头形式做了较为详细的规定,十分适合转向架构架的焊接疲劳强度设计,因而运用得越来越广泛[7]。国内也有较多学者和工程师对DVS 1612标准展开了研究[8-11]。
为得到符合DVS 1612标准的应力分布[12-13],需获得沿焊缝方向、垂直于焊缝方向的正应力和沿焊缝方向的剪应力,而一般有限元软件所得到的应力往往遵循全局坐标系或者是主应力和最大剪应力,必须对应力计算结果进行坐标变换。由于构架上焊缝数目较多,在空间中的角度分布也各异,因此这一过程往往十分复杂。本文直接利用焊缝名义应力的最大主应力和剪应力分量,基于DVS 1612标准,提出一种疲劳评估修正算法,并针对某转向架构架进行焊缝疲劳强度评估。
2 DVS 1612标准算法
根据DVS 1612标准,焊缝疲劳评估需要先得到基于焊缝方向的3种应力:平行于焊缝的正应力σ∥,垂直于焊缝的正应力σ⊥以及平行于焊缝的剪应力τ。而根据材料属性、应力比和接头形式,可以得到焊缝的3种许用应力:平行于焊缝的许用正应力,垂直于焊缝的许用正应力以及平行于焊缝的许用剪应力τzul。为了满足疲劳寿命,焊缝名义应力需要满足以下条件:

针对某转向架构架,对实际应用中受载荷较大的制动座、侧梁等部位进行焊缝疲劳强度评估。构架所用材料为S355钢[9],构架网格模型如图1所示。

图1 构架网格模型
将有限元计算结果变换为焊缝局部坐标系的应力分布后,得到σ∥、σ⊥、τ。制动座和侧梁上2条承受载荷较大的焊缝(焊缝1和焊缝2)的利用度沿焊缝长度的分布如图2和图3所示。
由图可以看出,制动座、侧梁的焊缝强度单向应力利用度小于1,综合利用度均小于1.1,满足疲劳使用寿命要求。
3 基于主应力和最大剪应力的疲劳评估修正算法

图2 焊缝1利用度沿焊缝长度分布
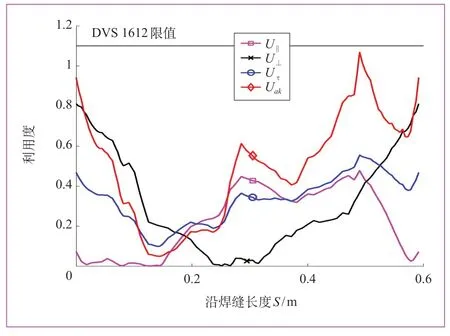
图3 焊缝2利用度沿焊缝长度分布
任意结构中某一点的应力均可以用其3个方向的主应力状态表达,将3个方向的主应力分别记为σ1、σ2、σ3,三者相互正交[14]。由于构架往往由钢板拼焊而成,焊缝处的应力基本为平面应力状态,因此钢板中某一点的主应力满足以下条件:垂直于钢板的应力|σ2|≈0,σ1、σ3处于板材平面内且正交分布。
某构架制动座焊缝处的主应力流线如图4所示,可以看到,主应力流线均分布于平面内,并且方向与焊缝走向基本一致;其主应力σ1、σ2、σ3沿焊缝长度方向应力分布如图5所示,可见垂直于钢板的应力σ2基本为0。
由于主应力方向与焊缝走向具有一定程度的重合,因此,可以将主应力σ1和σ3作为σ||和σ⊥的估计值,并用最大剪应力τ m替代平行于焊缝的剪应力τ[14]。主应力和最大剪应力状态可以直接从商业有限元软件中获取,避免了将全局坐标系下的应力转化为沿焊缝不断变化的局部坐标系下的应力,简化了计算过程。
根据DVS 1612标准,采用主应力和最大剪应力的疲劳评估方法对构架制动座、侧梁等危险焊缝进行疲劳强度评估,将式(4)转化为:
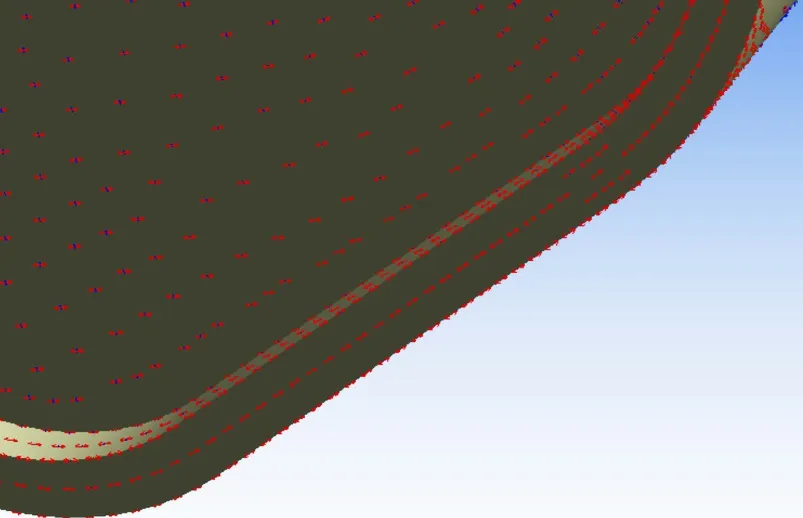
图4 制动座焊缝处主应力流线

图5 主应力沿焊缝长度方向应力分布

4 修正算法与标准算法和商用软件算法对比
4.1 计算精度对比
采用主应力和最大剪应力进行焊缝疲劳强度评估会带来误差[15]。下面分析该修正算法产生的精度影响。
设主应力方向与焊缝方向夹角为α,则主应力σ1、σ3和最大剪应力τ m与标准中的σ||、σ⊥、τ存在如下关系[14]:

记利用度函数:



图6 相对误差与夹角α 的变化关系
针对某构架承受载荷较大的2条焊缝(焊缝3和焊缝 4),分别采用 DVS 1612标准算法、商用软件LIMIT算法和本文修正算法计算焊缝疲劳强度利用度,结果如图7和图8所示。
由图可知,商用软件LIMIT算法所得到数值最大,结果最为保守(这是由于软件直接提取距离焊缝最近处的位移和应力),标准算法数值最小,本文提出的算法介于两者之间,既充分考虑了利用度,又不会造成估计不足的风险。
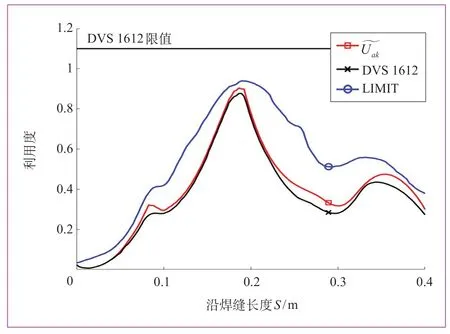
图7 不同算法下焊缝3的利用度对比

图8 不同算法下焊缝4的利用度对比
4.2 算法复杂度对比
由于商用软件LIMIT算法需要根据节点位移数据计算应力,而DVS 1612标准算法需要将全局坐标下的应力转化为沿焊缝方向的正应力、垂直于焊缝方向的正应力和沿焊缝方向的剪应力,因此二者均需花费较长时间[15]。为对比上文介绍的3种算法所需要的计算时间,采用复杂度的概念进行分析。本文的复杂度是指将算法编制为可执行程序后运行所需要的时间资源。
4.2.1 商用软件 LIMIT算法
根据LIMIT软件所采用的“sensor单元”方法[16],需进行以下步骤。
第一步:求sensor单元的位移,需进行42次加减法和42次乘法。
第二步:求sensor单元的应变和应力,需进行241次加减法和206次乘除法。
第三步:进行综合利用度计算,共需要4次加减法和12次乘除法计算。
由于加减法的复杂度为O(n),乘除法的复杂度为O(nlogn),因此对包含n个节点的焊缝,共需进行287n+260nlogn次计算[15]。
4.2.2 DVS 1612标准算法
针对DVS 1612标准算法需要进行以下步骤[16-19]。
第一步:求焊缝节点的局部坐标系的方向余弦(x轴沿焊缝方向),共需要进行107次加减法计算和63次乘除法计算。
第二步:求在局部坐标系下的方向应力,共需要进行36次加法和54次乘法。
第三步:进行综合利用度计算,共需要4次加减法和12次乘除法计算。
对包含n个节点的焊缝,共需要进行147n+129nlogn次计算。
4.2.3 修正算法
本文提出的修正算法只需要进行综合利用度计算,步骤如下。
第一步:用σ1替代σ||、σ2替代σ⊥,用τm替代τ,进行综合利用度计算,共需要4次加减法和12次乘除法计算。
第二步:交换σ1和σ2的位置,再次进行综合利用度计算,共需要4次加减法和12次乘除法计算。
第三步:比较第一步和第二步所得结果大小,并取较大值。
因此,对1个节点需进行8次加减法和24次乘除法计算,对包含n个节点的焊缝共需进行8n+24nlogn次计算。
图9对三者的计算复杂度进行了对比,可见本文提出的利用度修正算法的计算复杂度远低于另外2种方法。一个构架上焊缝节点数目达到数十万个,因此采用本文算法可以节省较多时间。
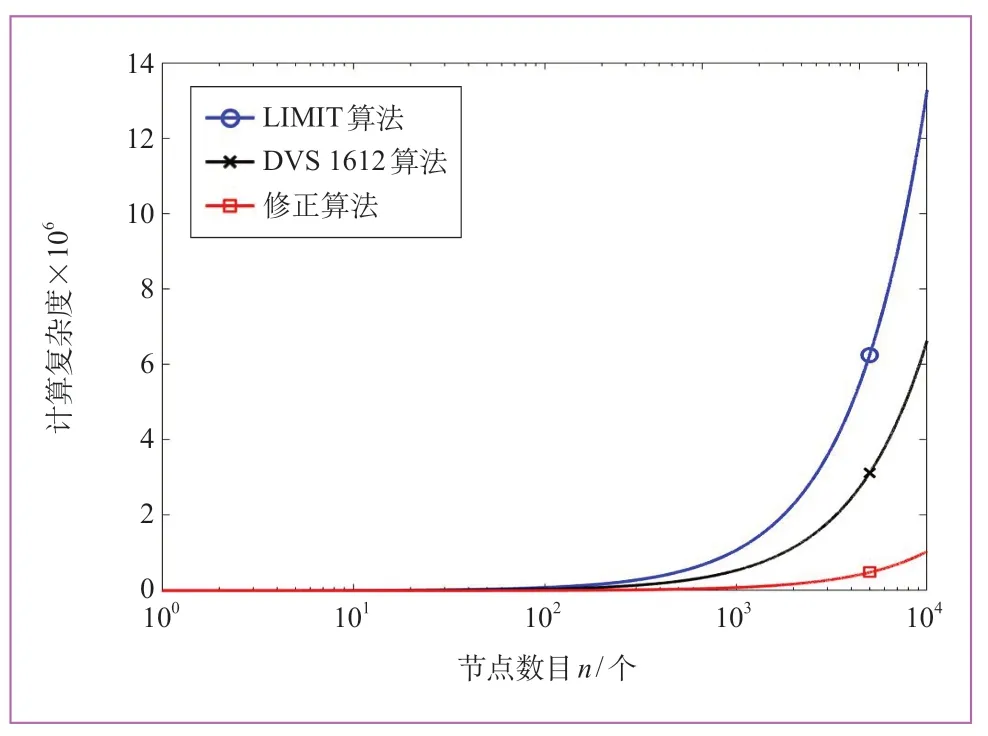
图9 不同算法计算复杂度对比
5 结论
本文基于DVS 1612标准多轴应力状态下的综合利用度,根据构架焊接结构特点,提出一种利用主应力和最大剪应力进行焊缝疲劳强度评估的修正算法,并对某构架关键部位进行了疲劳强度评估。通过对比DVS 1612标准算法、商用软件LIMIT算法和修正算法的精确度和复杂度,得出以下结论。
(1)由于焊缝处主应力方向与焊缝方向存在很高的一致性,因此采用基于主应力和最大剪应力的方法进行焊缝疲劳强度评估具有较高准确度。
(2)修正后的算法相比标准算法更加保守,但比商业软件利用率更高,满足工程实践的需求。
(3)修正后的算法复杂度相比商用软件算法和标准算法显著降低,提高了运算效率,具有较大的工程应用意义。
