基于重构控制分配的分布式电动车容错控制方法
2021-02-28丁凌志夏祖钶杨鄂川
欧 健,丁凌志,夏祖钶,杨鄂川
(重庆理工大学 a.车辆工程学院;b.机械工程学院,重庆 400054)
伴随着轮毂电机技术的发展进步,分布式驱动电动车以自身独特的结构形式及操控性能,已成为电动汽车的一个重要发展方向[1]。相较于传统车辆,集成主动转向的分布式驱动电动车具有较多的控制自由度,属于过驱动控制系统,系统中存在冗余执行器,当一个或多个执行器发生故障时,可以进行容错控制,重构剩余正常的执行器,保障车辆在故障后也具有一定的鲁棒性,提高车辆行驶的安全性与稳定性[2]。针对容错控制问题,Hayama等[3]提出双电机备份的控制思想,在高速行驶时对转向失效启用备份电机进行补偿,但这种控制对某种失效模式没有特定的控制逻辑。部分学者提出自适应滑膜控制思想使车辆对故障具有不敏感和抗干扰性[4],对系统进行被动容错控制可以在故障时保持一定的驱动力,但损失了车辆的部分性能。为进一步消除特定故障,文献[5]提出二次型规划算法设计分配控制策略,针对不同故障类型对剩余驱动力进行再分配。由于部分驱动电机故障情况下车辆仍然可以行驶,但稳定性与安全性无法得到保障,当执行机构发生故障时,故障轮无法提供预期的扭矩和转向角,并导致无法预测的后果。因此,对这类电动车进行容错控制是非常重要的。
基于分布式驱动电动车过驱动系统存在的冗余现象,本文提出了一种容错控制算法,上层基于模型预测控制的运动跟踪层,下层针对不同故障信息,提出一种基于线性二次规划的最优控制分配,通过对正常轮胎的制动/驱动转矩优化分配,从而跟踪车辆的期望响应。
1 车辆动力学模型
本文主要针对车辆横摆稳定性进行研究,采用模块化建模思想建立整车7自由度车辆模型[6],如图1所示。其中7自由度主要包含横向、纵向、横摆运动以及4个车轮的旋转运动,由牛顿第二定律得车辆的动力学方程为:

式(1)中:vx、vy分别为车速的纵向与侧向分量;轮、左后轮、右后轮的纵向力,Fy=[FyflFyfrFyrlFyrr]T分别为4个车轮的侧向力,本文中各车轮的纵、横向力可由Pacejka魔术轮胎公式[7]计算得出;γ为横摆角速度;Bx、By是车辆模型的固有参数[8]。

图1 7自由度车辆模型示意图
车轮在滚动过程中的动力学方程表达为:

式(2)中: ωi为各轮旋转的角加速度;Tdi为各车轮分别受到的由轮毂电机产生的驱动转矩;R为车轮滚动半径;Tbi为各个车轮制动器产生的摩擦力矩;Jωi表示各车轮的转动惯量。
2 控制器结构设计
为提高电动执行机构故障后车辆的操纵稳定性,提出了一种容错控制方法,如图2所示。该控制方法包括3个部分:故障诊断模块、运动控制模块和重构控制分配模块[9]。运动控制器以线性2自由度车辆模型为参考模型,以参考横摆角速度和质心侧偏角作输入,采用模型预测控制的方法,使前文所搭建的车辆模型能有效跟踪期望的运动状态,计算出所需的总的附加力与附加力矩,由下层的重构控制分配器将总的需求力与力矩按一定规则分配给每个车轮。无故障时,以轮胎稳定性裕度最大化为控制目标,采用名义控制分配率。故障发生时,根据相应的故障类型,以轮胎稳定性裕度并结合实际故障状况重构控制分配率。本文着重于研究驱动电机容错重构控制分配方法,假设所期望的车辆状态可以被测量或估计、故障信息已知。

图2 容错控制结构框图
2.1 运动控制器设计
2.1.1 预测模型
模型预测控制是基于模型初始条件对系统未来状态进行预测,并通过实时反馈来进行滚动优化,不需要精确的模型。因此选用线性2自由度车辆模型作为预测模型,以附加前轮转角和附加横摆力矩作为控制输入,状态空间方程为:

式中:

其中:a、b分别表示质心与前后轴之间的距离;δd、δa分别表示前轮转角与附加前轮转角;k1、k2为前后轴侧偏刚度;ΔM为附加横摆力矩。
2.1.2 预测方程
以系统当前的状态作为输入,通过预测方程预测出系统未来的状态。对式(3)进行离散化,将离散后状态空间方程改写成增量形式,有:

根据式(4),设定预测时域为p,控制时域为m,m≤p,假设在控制时域之外,控制量不变,即Δu(k+i)=0,i≥m。
当前k时刻下x(k)和y(k)为已知条件,由式(4)可以对k+1到k+p时域内的状态进行预测,从而进一步解得系统未来p步的预测输出向量序列,表示为:


2.1.3 优化求解
本文的控制目标是得到期望的运动状态,即保证车辆输出最大化接近于参考值,同时保持控制动作平缓输入,运动控制器的目标是使系统输出跟踪期望输出,采用二次型表示的目标函数为:
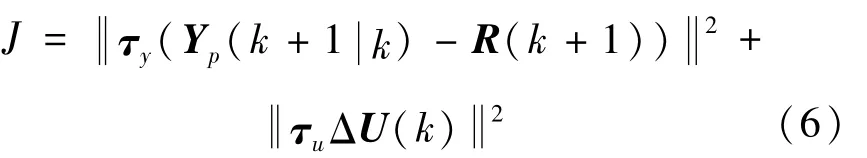
式(6)中,τy、τu为加权系数矩阵。考虑到执行器约束条件,对输入量和输入增量进行约束,即:

进行采样周期优化求解,最终得到最优控制输入增量为:

将控制系统输入的第1个量作为实际控制输入增量施加在所建立的车辆模型上,则有:
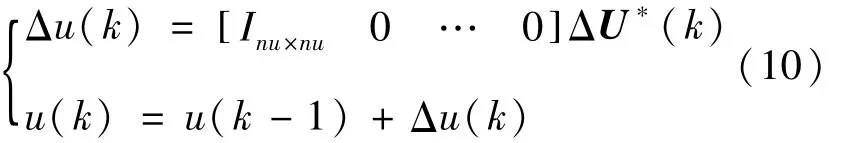
反复以上优化求解过程,直至求解结束。
2.2 重构控制分配器
重构控制分配器就是将运动跟踪层所求得的附加横摆力矩和总的纵向力需求,采用合适的分配算法把期望转矩分配给各个执行电机,实现车辆的横摆稳定性控制[10]。根据控制分配律决策出每个轮的轮胎纵向力Fx,在监测系统识别无故障的情况下,重构控制分配器采用名义控制分配方法;在车辆运行过程中发生某种故障时,重构控制分配器采用与该故障模式对应的重构控制分配律。
2.2.1 名义控制分配算法
无故障时,采用名义控制分配算法,以各轮轮胎利用率平方和最小为优化控制目标,旨在最大化轮胎稳定性裕量,从而保证车辆的稳定性[11]。其中,由于在工程上暂时不能对车轮的侧向力进行直接控制,简化为各个车轮纵向利用率平方和最小,目标函数为:
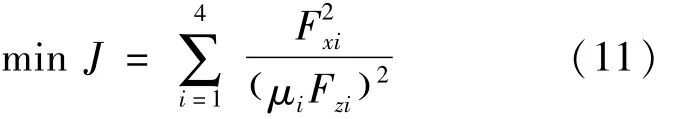
需要满足动力学约束有:

地面附着条件的约束为:
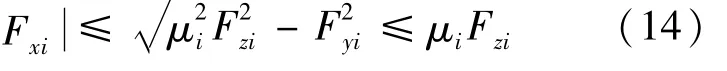
考虑电机的转矩输出约束,则有:

式(14)、(15)中:μi为路面摩擦系数;Tmax为电机当前转速n下最大输出转矩。
根据优化目标和约束条件,将求解转化为加权最小二乘问题,为方便计算上述带约束问题的目标函数,采用有效集的标准形式来求解,有:

通过求解获得各车轮上的轮胎纵向力Fx,作为名义的控制输入。
2.2.2 重构控制分配算法
本文研究的重构控制分配算法是基于故障观测器所观测到的故障信息,侧重于诊断某一驱动系统的驱动力是否能正常输出。针对一个或多个驱动执行器故障后,通过协调控制其他正常驱动系统进行轮胎力的重构分配,保障车辆的期望轨迹,提高车辆故障后的横摆稳定性[12]。重构控制器一方面对故障执行器进行限制,防止故障进一步扩散,另一方面又针对不同的故障模式,采用相应的重构控制分配律对剩余正常的驱动系统进行转矩分配,使执行器总的输出力与力矩依然满足上层运动控制器计算得到的虚拟控制量要求。
本文中提到的重构控制分配流程如下:
1)执行器无故障时,以名义控制分配率作为执行器控制输入;
2)根据故障信息,判断出失效模式;
3)当执行器故障时,根据相应的失效模式,采用相应的重构控制分配律作为执行器输入[13]。分配流程如图3所示。
根据电机的不同失效模式,重构控制分配方法如表1所示。分别讨论了在单个电机失效,异侧同轴双电机失效,异侧不同轴两电机失效、同侧两电机失效及2个以上电机失效等5种失效模式。在单轮电机故障情况下,考虑驱动电机故障约束,以提高轮胎的附着裕度为目标;在异侧同轴与异侧不同轴电机失效情况下,仅剩余2个可控自由度的轮胎力,无法满足车辆纵向力需求,此时着重保持故障后车辆的侧向和横摆稳定性特性;在同侧两电机及2个以上电机失效情况下,考虑到故障后车辆的安全性,进行紧急制动控制。

图3 重构控制分配流程框图

表1 重构控制分配方法
3 仿真实验
在Matlab/Simulink中搭建集成容错控制器和7自由度整车模型,轮毂电机模型采用能够体现其特性的简化模型,其外特性曲线高速恒扭矩,低速恒功率[14]。Matlab/Simulink整体仿真结构如图4所示,针对执行器不同的失效模式,为验证本文提出容错控制算法的有效性,分别讨论在单轮和双轮失效情况下汽车的横摆稳定性。车辆仿真参数如表2所示。

图4 Matlab/Simulink整体仿真结构框图

表2 整车参数
3.1 角阶跃转向工况(单轮失效)
为验证车辆在角阶跃转向时容错控制算法的有效性,设计工况为:初始车速为80 km/h,路面附着系数为0.8,在2 s时前轮转角阶跃输入1°,t=2 s时,左前轮电机完全失效,仿真结果如图5所示。
由图5(a)可以看出:在2 s时左前轮电机失效,无控制车辆横摆角速度持续增加,最大值达到了0.46 rad/s,已经超出了车辆横摆稳定性的范围,车辆出现失稳状态。容错控制下横摆角速度曲线有稍许的波动,但很快恢复稳定且不断靠近期望值曲线,横摆角速度最大值为0.14 rad/s,在稳定可控范围以内。由图5(b)可以看出:当左前轮失效时车辆的质心侧偏角将偏离正常值,无法保障车辆的横摆稳定性。红色与蓝色曲线分别为容错控制下质心侧偏角与参考模型的期望值,两者在2 s时有稍许的波动,随后都趋于稳定值,且容错控制曲线更快地趋于稳定。容错控制下质心侧偏角最大绝对值为0.012 rad,期望值为0.020 rad。可见容错控制下质心侧偏角比期望值更低,对车辆的横摆稳定性控制效果更好。由图5(c)可以看出:在t=2 s时,纵向车速发生抖动,但容错控制使车辆很快就恢复到目标车速,表明容错控制在保证车辆横摆稳定性的同时,还能兼顾车辆的纵向速度,不改变驾驶员意图保持车辆安全稳定行驶。图5(d)表示容错控制下电机转矩分配曲线,0~2 s内按照名义控制分配,车辆正常稳定行驶,在2 s时,左前轮电机失效,根据检测到的故障信息,车辆开始采用重构控制分配率。左前轮电机转矩马上置零,左后轮电机转矩立刻增大以弥补附加横摆力矩需求。同时,右前轮电机与右后轮电机转矩也有少量的增加,因为当一个电机失效时,总的转矩输出减少,提供总的纵向力也减少,容错控制进行协同其他电机的转矩,在弥补横摆力矩需求的同时,保证车辆总的纵向力,所以每个车轮单机转矩都有增加。

图5 角阶跃工况仿真结果
3.2 正弦转向工况(双轮失效)
当双轮电机发生失效时,只有剩余两驱动电机工作,车辆的稳定性受到了巨大的威胁。为验证容错控制算法的有效性,设计了双轮失效的双移线工况进行仿真对比实验。具体工况为:车辆车速为80 km/h,路面附着系数为0.8,方向盘转角如图6所示。在时间t=2 s时左前轮与右后轮电机同时失效,仿真实验结果如图7所示。

图6 前轮转角输入

图7 正弦转向仿真结果
从图7(a)、图7(b)可以看出:在正弦转向工况下,无控制车辆的横摆角速度和质心侧偏角峰值分别为0.3 rad/s和0.03 rad,车辆极易失稳,从而失去控制。容错控制下,二者相比无控制状态更接近于期望值,且维持在车辆稳定性范围内。表明了在双轮胎电机失效的情况下,容错控制车辆能有效地跟踪期望横摆响应。从图7(c)可以看出:无控制下的车辆横向位移不断增大,在10 s仿真步长内,横向位移达到8.6 m,此时车辆已经完全偏离了预想轨迹。容错控制下车辆在转向开始后,横向位移开始增大,达到最大值2 m后,随着正弦转向的结束,车辆横向偏移逐渐减小,保证车辆按预定轨迹行驶,提高了车辆的通过性。图7(d)为容错控制下电机的转矩分配图,在t=2 s时,左前轮与右后轮电机转矩同时变为零,右前轮电机转矩不断增大,左前轮电机转矩反向增大。在容错控制中,当双轮电机发生失效时,电机转矩进行了重新分配,基于重构控制分配方法,立即限制失效电机的转矩输出,同时分配剩余两电机转矩弥补车辆不足转向,同时还要保证总的纵向力需求。因此,剩余两电机转矩同时反向增大来维持车辆的稳定性。其中,右前轮与左后轮电机转矩都在最大值处受到限制,是因为考虑到电机的安全性,以电机的额定转矩范围内进行输出。
4 结论
1)针对分布式驱动电动车横摆稳定性容错控制问题,本文总结了驱动电机的各种失效模式,并提出了相应的控制目标及约束条件,通过仿真验证了在单轮以及双轮驱动失效后,容错控制策略能更好地保持车辆期望的横摆角速度、质心侧偏角以及减少车辆的跑偏量。
2)重构控制分配层,采用线性二次型方法进行轮胎力的优化分配,在执行器故障后重构控制分配率,通过设计故障时的离线仿真表明,在车辆发生故障时,容错控制能有效地维持车辆的期望轨迹,防止故障进一步扩大且维持较好的稳定性与操纵性。
3)本文根据故障信息,总结了驱动电机的失效模式,但没有考虑到转向电机的失效或者传感器的失效情况,以及几种故障耦合下的容错控制需进一步探索。
