气液耦合激振下的空化泡动力学特性与试验研究
2021-02-28张慧贤郭兆锋杨海军布占伟
张慧贤,郭兆锋,杨海军,布占伟
(1.洛阳理工学院 机械工程学院,河南 洛阳 471023;2.上海倍伺特自动控制设备有限公司,上海 201818)
液压系统的清洁度是影响系统可靠性的关键因素。制造或装配过程中残留于系统内部的污染物会在系统内部产生沉积,堵塞节流孔和加速元件磨损[1-2]。常规的物理清洗方法是将待清洗的液压系统拆卸之后,对阀块等组件用毛刷及清洗油进行逐件去污之后再更换液压油。该方法易造成系统二次污染且效率低下。而化学清洗的排放物会对环境造成污染,因此,探索有效的物理清洗方式符合国家节能减排相关政策。
物理清洗中常见的超声波清洗是利用超声波使液体中的微气核空化泡发生振动,通过空化作用产生的巨大能量对污物进行分散与剥离,从而达到清洗目的。Rayleigh[3]建立了不可压缩流体中气泡动力学模型,Plesset[4]在考虑流体压缩性后对Rayleigh方程进行改进,得到了著名的R-P方程[5];黄明哲等[6]研究了超声波作用下空化泡在不同声压下的泡壁运动,揭示了空化泡内部压强与声压的关系;付英杰等[7]采用拉格朗日有限体积法对气泡群振荡过程及辐射噪声进行数值模拟。但在实际应用中超声波衰减严重,因此超声波清洗只适用于近距离小范围,不适用于较长距离的液压管道。在通气空化泡的研究中,王复峰等[8]采用数值模拟和试验研究相结合的方法,对通气空化作用下多相流的动态特性进行了研究与分析;张孝石等[9]研究了水下通气航行体云状空泡的脉动特性,得到了通气航行体表面压力在不同空化数下通气空化的频域特征。通气空化过程涉及复杂的多相流及非定常等问题,而目前在民用管道清洗中的气脉冲清洗[10-12]就是利用流体自身空化与通气空化相结合的复杂的多相流共同作用对管道内壁进行清洗。
综上,受超声波清洗与民用管道清洗的启发,本文中提出将外加气体与液压油结合起来的新型激振方式,以气体波动发生器作为激励源,建立了气液耦合激振下的通气空化泡动力学模型。开发了气液耦合激振试验系统,数值模拟了气脉冲与液压油形成的通气空化泡发生、生长和破灭的动力学过程,并与试验检测结果进行对比分析,探索气液耦合激振方式在液压系统污染物去除方面的可行性。
1 激振原理
图1所示的气液耦合激振试验系统由液压系统、气压系统与电气控制系统组成。液压系统包括液压泵站、电磁换向阀、管路和背压阀等;气压系统包括空压机、气动三联件、波动发生器和气动管路等;电气控制系统通过PLC进行程序控制,对液压泵的流量、电磁换向阀以及气体波动发生器的启闭频率等进行控制。气体通过减压阀进入波动发生器,波动发生器相当于能快速启闭的阀门,变频器控制电机驱动波动发生器产生脉动频率可调的气压波;从液压泵流出的液体通过电磁阀控制,形成的脉动流体与气压波交替混合。
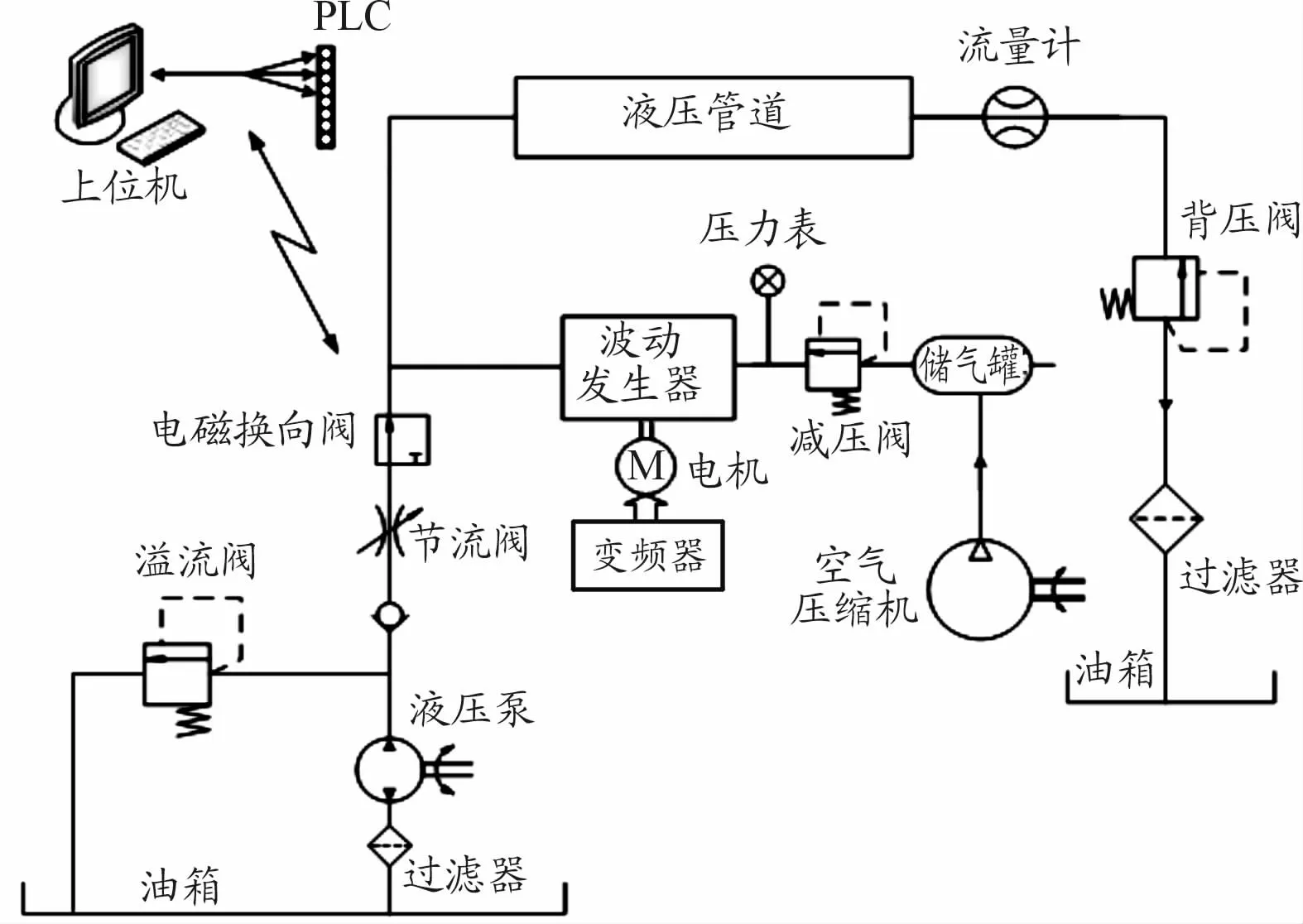
图1 气液耦合激振试验系统组成示意图
试验系统中液压泵额定转速为1 450 r/min,排量为63 mL/r,额定工作压力为31.5 MPa。用于驱动波动发生器的电机功率为1.5 kW,空压机额定压力为10 MPa,电磁溢流阀公称压力为20 MPa,与背压阀联合调节液压系统压力。
2 气泡动力学模型
如图2所示,气液发生混合,P0为液体静压力,Pa为气体压力。假设液压油不可压缩,气泡初始半径为R0,气泡内外初始压力Pin和Pout分别为:
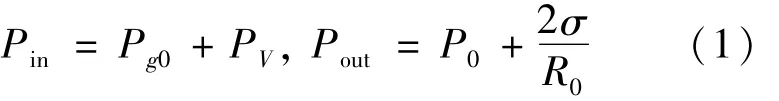
式中:Pg0为泡内气体压力,且泡内气体为理想气流体中的气泡受力平衡时,泡内外压力相等,即的脉动气压Pa与液体混合时,Pa=PAsin wt,PA为气体峰值压力,w为波动频率。当气泡发生空化作用时,气泡半径由R0减小为R,对应的泡内气体压力由Pg0变为Pg。将气泡的运动过程视为绝热过程,由理想气体的绝热方程可结合式(1),气泡内外新的压力P′in和P′out分别为:
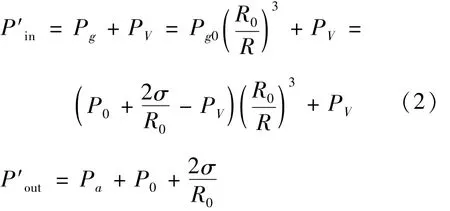
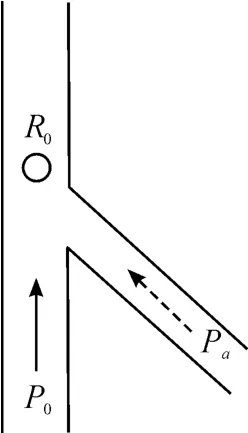
图2 气液耦合示意图
液体移向气泡收缩空间所获得的动能为
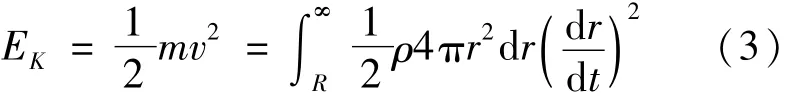
对于不可压缩的流体,气泡收缩的体积等于液体填充的体积,即4πR2d R=4πr2d r,则有R2d R=
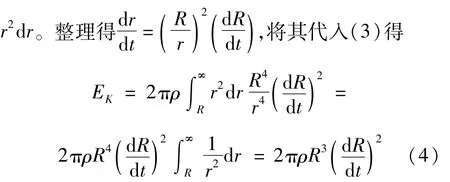
由于气泡所受到的收缩压力P′out克服膨胀压力P′in所做的功等于液体获得的动能,即
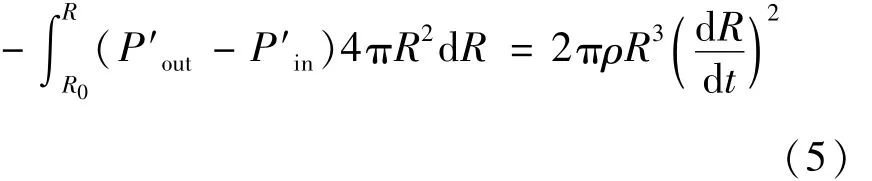
两边对R微分得
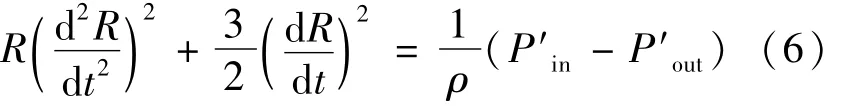
将式(2)代入式(6),得到绝热状态下气泡运动方程为
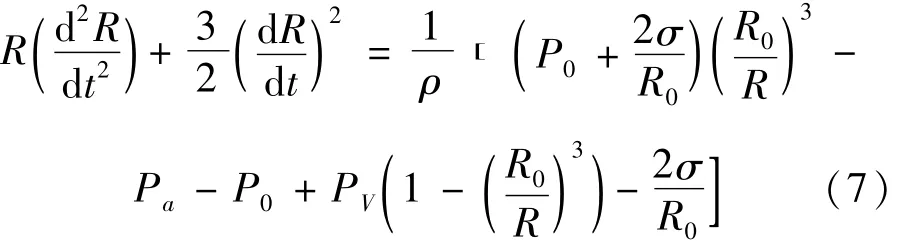
考虑到气泡运动过程中的能量黏滞损耗,式(7)修正为
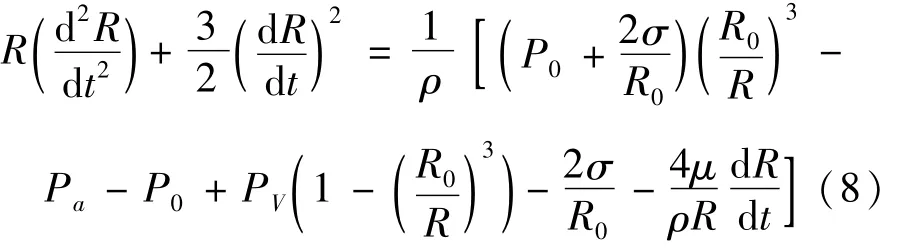
式中:μ为液体的黏滞系数;4μ/ρR为黏滞损耗项。
3 数值模拟与分析
3.1 激励气压对气泡空化过程的影响
通过数值求解非线性常微分方程(8),研究气泡在液体中发生空化作用的动态过程。采用变步长4阶Rung Kutta法[11]将式(8)所示的2阶常微分方程化为1阶微分方程组。气体为25℃的空气。为便于试验观测,液体采用二甲基硅油,2种流体参数如表1所示。

表1 25℃时气泡与液体初始参数
设气体压力Pa=PAsin2πft,PA为气体静压力,f为驱动波动发生器的变频器频率。为研究气泡在不同气压下半径及压力的变化,假设气泡初始半径R0为3 mm,变频器频率f为30 Hz,调节电磁溢流阀与背压阀使液体的静压P0为4 MPa,调节气体减压阀,取气压PA分别为0.04、0.4、1 4、3.0、3.6和3.8 MPa时,气泡稳态空化过程如图3所示。
图3表明:当变频器频率及气泡初始半径R0不变时,空化气泡生长半径R随气压的增大而增大,空化效应增强。这是因为在脉动气压Pa的正压区,气压PA的增大使气泡的拉伸作用增强,气泡半径R变大。而在脉动气压Pa的负压区,气泡受到的压缩作用增强,导致气泡半径R的减小幅度也增加,气泡空化作用加剧。图3(a)中,增大气压PA至3.6 MPa,气泡呈现出有规律的膨胀与压缩,但没有崩溃,空化过程表现为稳态。图3(b)中,增大气压PA至3.8 MPa时,气泡出现了剧烈的高频振荡,具体出现在拉伸的初期与压缩的末期,空化过程表现为欠稳态,但2个周期内出现了2个清晰的波峰,空化过程依然属于稳态过程。因此,图3(a)、(b)中反映了不同气压下气泡从稳态到欠稳态的过程。由此可以得出,气压的增大使气泡的空化作用加强。在本试验系统中,由于气压是通过减压阀调节的,因此气泡的空化过程是可控的。
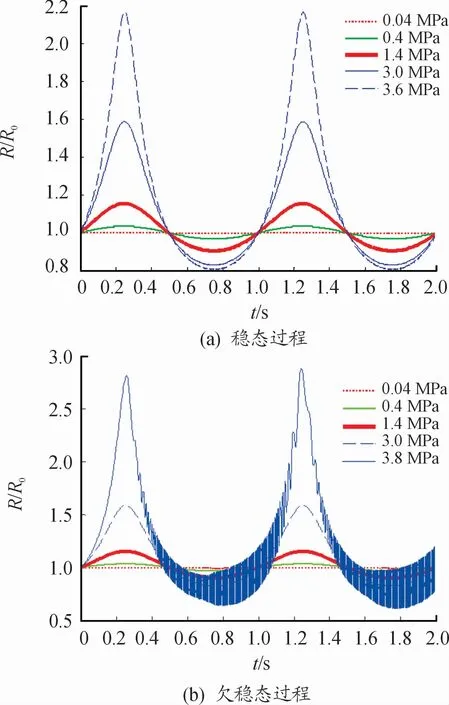
图3 不同气压下气泡稳态空化过程曲线
图4 (a)中,增大气压PA至3.9 MPa,气泡在经过了1个波峰的膨胀之后,压缩阶段出现了剧烈的高频振荡,表现为非稳态,在崩溃之后又伴随着气泡的生长、反弹、崩溃及再生长的复杂过程。在经过约1.4个周期之后,气泡完全破灭,之后再无继续生长。图4(b)中,增大气压PA至4.0 MPa,即PA=P0时,气泡在经过了1个波峰的膨胀之后破灭,紧接着又发生了1次生长之后完全破灭,空化过程变为瞬态过程。当气压PA增至4.2 MPa,即PA>P0时,气泡半径有了大幅度的膨胀,之后完全破灭。因此,图4(a)、(b)反映了空化气泡随着气压的增大,从非稳态到瞬态的过程。显然,非稳态空化有空化的持续产生,但气泡膨胀半径较小,而瞬态空化气泡膨胀半径较大,空化作用较剧烈。因此,在实际中可根据不同工况调节系统激振参数,以使其具有更好的空化效果。
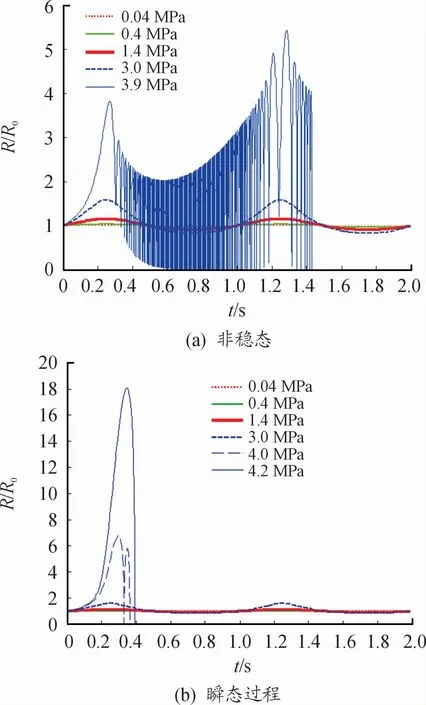
图4 不同气压下气泡瞬态空化过程曲线
3.2 气泡内部压强的变化
保持气泡初始半径R0为3 mm,变频器频率f为30 Hz,液体静压P0为4 MPa。图5为气压PA分别为0.4、1.4、3.0、3.9、4.0和4.2 MPa时气泡内部压强的演化过程。图5(a)表明当发生稳态空化时,空化泡内部压强随气压的升高而升高,且呈有规律的振动,表现为内部压强的稳态过程。此外,对比图3发现,空化泡内部压强的变化与空化泡膨胀同压缩的运动过程相反,即空化泡膨胀半径最大时对应的泡内压强最小,当空化泡被压缩到最小半径时泡内压强最大。图5(b)表明当气压增大到3.9 MPa时,稳态空化变为瞬态空化,气泡崩溃后内部压力迅速释放出来,持续时间非常短暂,显示了空化泡内部压强的瞬态过程。当气压增大到与液体静压相等的4.0 MPa时,泡内压强达到最大,之后随着气压的增大泡内压强迅速减小。
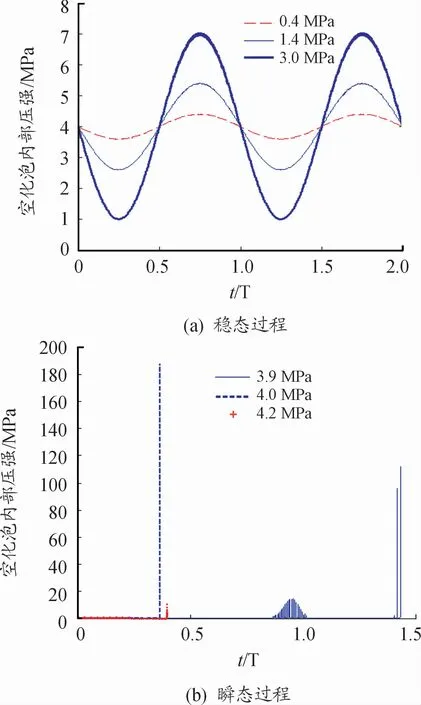
图5 不同气压下空化泡内部压强
3.3 与ANSYS Fluent的仿真对比
图2 所示气液混合处液压管道内径D=15 mm,气体管道内径d=10 mm,气液混合后进入图1所示长度l=15 m的液压管道。将气相与液相视为拟连续介质,通过分析气液两相之间的相互作用,在ANSYS中设置液相、气相模型为标准k-ε二方程模型,混合后的两相流模型采用VOF模型,其中体积分数采用隐式时间离散格式求解。对图2几何模型采用三维软件建模并划分网格后,导入ANSYS中采用SIMPLE算法对双流体模型进行数值迭代计算,网格图见图6。

图6 网格图
在ANSYS中,入口边界条件定义为Pressure inlet,出口边界条件定义为Pressure outlet。采用标准的k-ε湍流模型与增强的壁面函数法,以及轴对称的分离隐式求解器对气液耦合进行数值模拟。为表征脉动流体的实际特性,将通过电磁换向阀的液体与波动发生器作用下的气体采用UDF(用户自定义函数)定义。
3.3.1 压力曲线
为形成气液连续激振的压力场并与试验结果进行对比分析,在数值模拟中,图2所示的进气口和进油口采取气液交替混合的方式分别通入1、3、5 MPa压力的流体。在ANSYS Fluent中设置25℃的空气与液体,2种流体参数如表2所示。

表2 25℃时ANSYSFluent中流体参数设置
假定在系统中循环通入3 s的气体和5 s的液体,则不同流体压力下,气液混合后管道中部流体压力的时程曲线如图7所示。图7(a)中通入管道中的气体和液体压力均为1 MPa时,混合之后流体的激振压力出现了小幅波动。图7(b)表明,当通入气体和液体的压力为3 MPa时,混合之后流体的激振压力出现了脉动。当通入气体和液体的压力为5 MPa时,混合之后激振压力出现了较大波动,如图7(c)所示。由此可见,管道中部混合之后流体的激振压力随混合之前气液初始压力的增大而增大,且压力的增大导致混合之后流体的压力波动也越大。
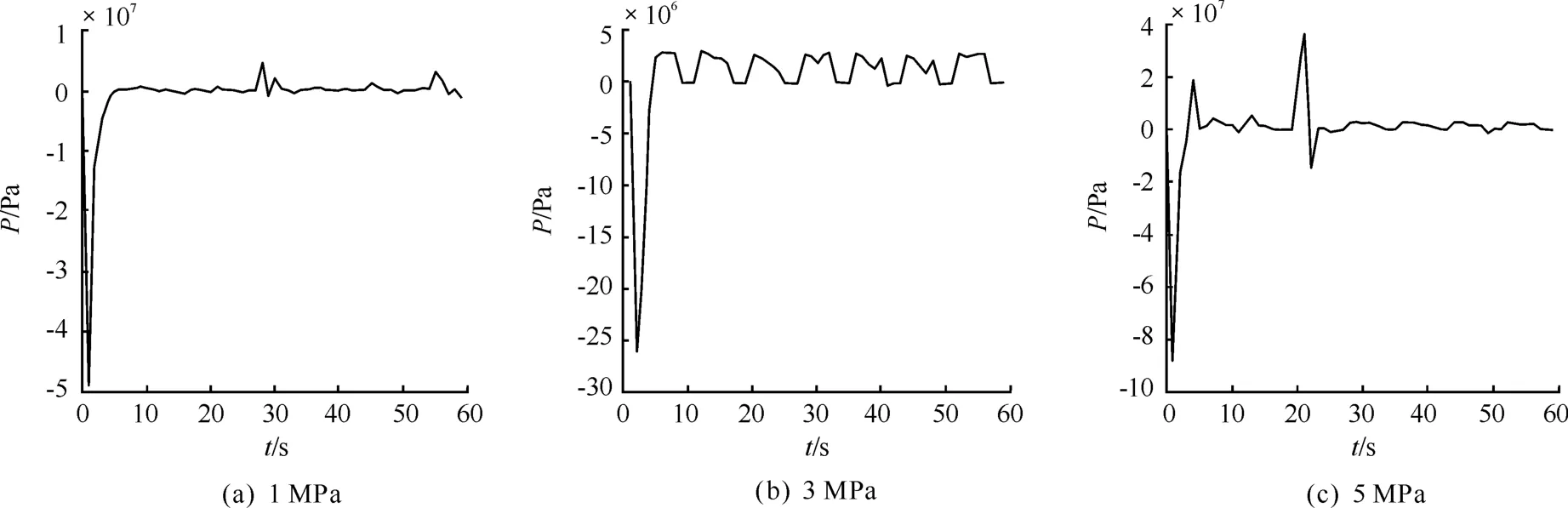
图7 不同流体压力下混合流体压力的时程曲线
3.3.2 压力云图
图8(a)~(c)分别为ANSYS Fluent中混合流体在不同初始压力下的压力云图。从压力云图的分布来看,混合流体压力随气液初始压力的增大而增大。对比图8(a)~(c)可以发现,气液初始压力的增大将导致混合后流体的压力波动更加明显,与图7中不同流体压力下混合流体压力变化曲线是一致的。
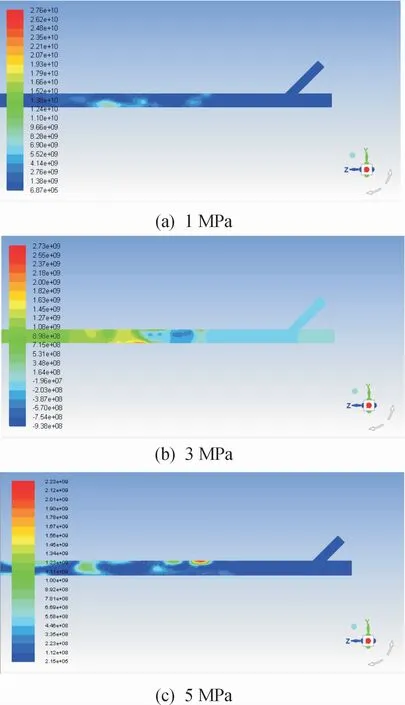
图8 不同流体压力下混合流体压力云图
4 试验对比分析
图1所示试验系统中,采用PLC控制的方式,通过气体波动发生器和电磁换向阀分别控制气体和液体交替混合。试验系统中气体为25℃的空气,液体为二甲基硅油,2种流体参数如表1、2所示。压力变送器(20 MPa,两线制4~20 mA)安装在气液混合后的管道中部,数据采集后变送器电流信号变换为电压信号接入USB-6005高速数据采集卡。为消除高频干扰,首先采用最小二乘法消除振动信号趋势项,然后采用五点滑动平均法对压力信号进行滤波处理。
图1试验系统中,从进气口和进油口分别通入3 s的气体和5 s的液体,则流体压力为1、3、5 MPa时,实测的管道中部混合流体压力变化时程曲线如图9(a)~(c)所示,(d)为滤波后不同工况的对比。
从图9(d)可以看出:随着进气口和进油口流体压力的增大,混合流体的压力也逐渐增大,表明混合流体的压力可通过流体初始压力进行调节。图9的实测压力曲线与图5的仿真曲线具有相同的变化趋势,并与图7激振压力的数值模拟结果具有较好的吻合度。由此表明通气空化泡所产生的气液耦合激振压力的可控性,这种可调可控的气液耦合振荡流的产生将剥离并去除管道内壁的污染物,有效提高液压系统的清洁度。
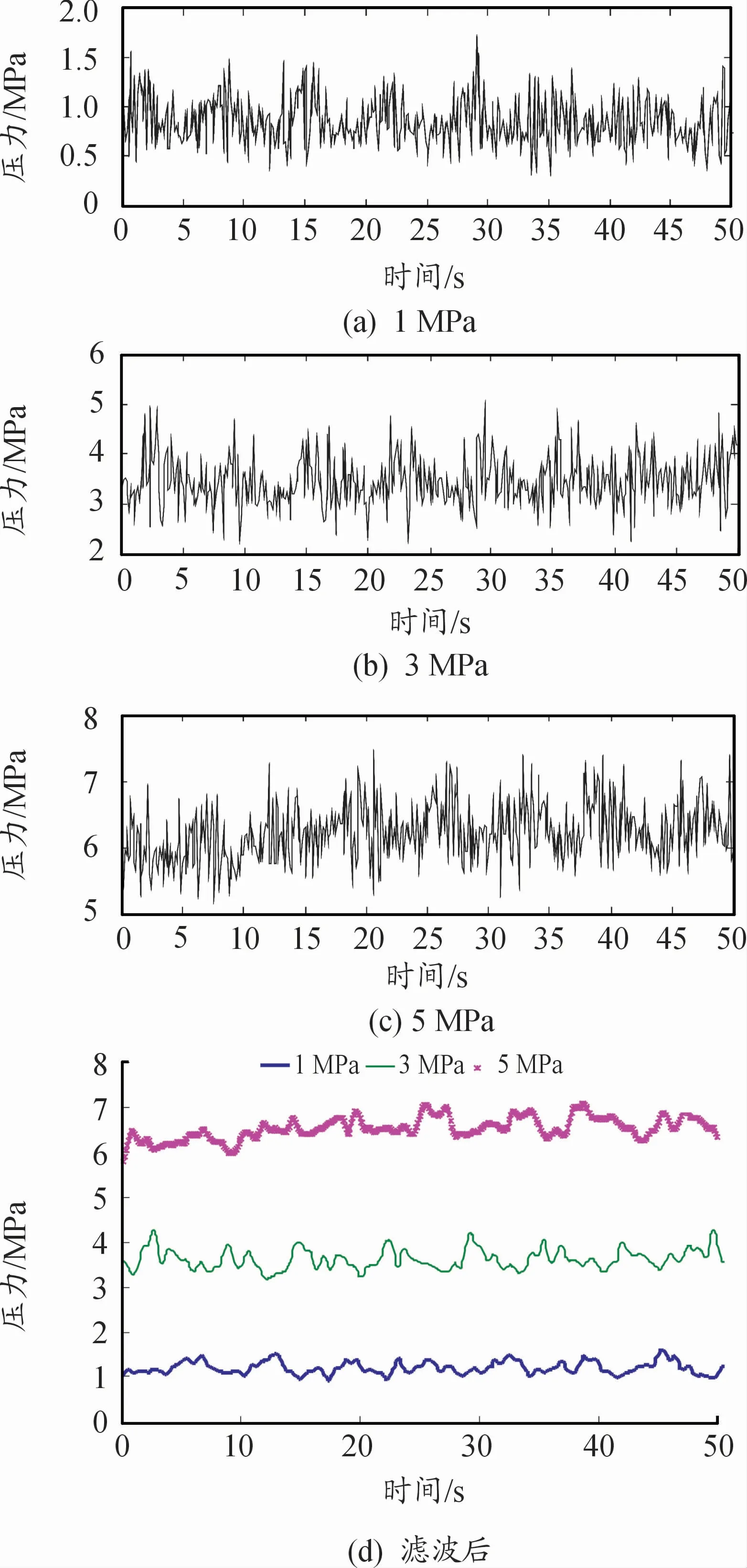
图9 实测激振压力
5 结论
1)提出了一种气液耦合激振方式,通过控制气脉冲与液压油形成的通气空化作用对液压系统内部污染物进行分散与剥离。以气体波动发生器作为激励源,开发了变频气液激振试验系统。
2)建立了波动发生器作用下的通气空化泡动力学方程,数值模拟了气液耦合激振作用下气泡的动力学过程,揭示了通气空化泡发生生长和破灭的动力学过程。表明随着气压的升高空化效应增强,气泡空化过程会从稳态向瞬态转变,空化作用增强。
3)采用ANSYS Fluent计算了通气空化泡的流场压力及分布云图,采用压力变送器及数据采集卡对流场的激振压力进行采集及滤波处理,将试验数据与仿真结果进行对比分析,数值模拟结果与试验结果具有较好的吻合度。
4)气液耦合激振方式为液压系统的清洗提供了新方法,表明气液耦合激振作用下通气空化泡空化过程的可控性,为复杂液压系统的在线不拆卸清洗研究提供了参考。
