某变截面连续刚构箱梁结构受力验证与分析

■陈财焕

（福建省交通科研院有限公司， 福州 350005）

变截面梁是指在弯矩较大处采用较大截面，在弯矩较小处采用较小截面的沿轴线变化的梁；与等截面梁相比，变截面梁节省材料，减轻梁本身重量。连续刚构桥梁是大跨径桥梁建设中常用的一种结构体系，其主梁为连续梁体并与桥墩固结，综合了连续梁桥和刚构桥的受力特点，故连续梁体的受力较为复杂。 箱形断面具有很好的整体性、结构刚度，特别是其抗扭能力很强。 因而大部分大跨度的连续刚构桥采用变截面箱形的横断面形式[1]。 在判定其箱梁结构受力情况时，一般采用理论模型分析和桥梁荷载试验两种结合方法。 而桥梁荷载试验是最直接反映箱梁结构实际受力情况，不仅可以对箱梁难以模拟的部位进行最简单且显而易见的受力情况判定，还可以对桥梁结构健康状况做出总体的性能评价和承载能力评定。 当然，理论模拟分析是荷载试验的科学依据，荷载试验中作用的等效、作用位置及作用大小均由理论模拟进行界定。 因此，变截面连续刚构箱梁主要控制截面结构受力需要荷载试验和理论模型分析两种方法协同验证性分析，才能精确其结构受力情况。

1 工程实例

某混凝土梁桥的桥面标准宽度为18.5 m=0.50 m（人行道）+2.00 m（硬路肩）+3.50 m（行车道）+3.50 m（行车道）+3.50 m（行车道）+3.50 m（行车道）+2.00 m（硬路肩）+0.50 m（人行道）。 全桥共设五联：3×35 m+3×35 m+3×40 m+（62+110+62）m+2×40 m，上部结构采用预应力砼T 梁+预应力砼变截面箱梁连续刚构+预应力砼T 梁结构。 其中第四联为变截面连续刚构箱梁。 主梁、翼缘板、横隔板、湿接缝、现浇连续段均采用C50 砼， 所用预应力钢筋为Strand1860；下部桥墩采用三柱式墩。 墩身、墩帽均采用C30 砼，桩基础采用C30 砼。 设计荷载等级为公路-I 级。 变截面箱梁截面尺寸见图1。

2 有限元模型

变截面连续刚构箱梁主要构件为箱梁和墩柱。梁体结构中含有混凝土、 普通钢筋及预应力钢筋，箱体顶板设有横向预应力，底板及腹板有纵向预应力，整个箱体结构受力较为复杂。 故可运用大型数值分析软件Midas 根据施工工序和设计材料属性建立变截面连续刚构箱梁结构的有限元模型，计算恒载和活载施加过程中其内力的分布规律[2-3]。

2.1 计算参数

（1）恒载。 混凝土容重取26 kN/m3，横隔板自重以均布荷载加载到主梁相应位置。（2）活载。汽车荷载采用公路-I 级， 四车道横向折减系数为0.67，按偏载和正载两种方式布置车道。（3）荷载组合。按基本组合对设计活载产生的最不利内力值进行计算。

2.2 边界条件

桥梁各构件均采用梁单元模拟，材料特性与截面特性根据实际所用材料参数输入。 按照该桥竣工图纸， 应用桥梁Midas 计算软件进行建模计算，计算模型见图2。而后添加边界条件，连续梁两端与实际道路连接处相对位移较小，故连续梁两端添加的边界条件为采用一般支承， 约束其线位移自由度，地基对双肢薄壁墩约束条件类似，而连续梁与下方双肢薄壁墩之间的边界条件均采用弹性连接。

图2 计算模型

2.3 受力分析注意事项

使用Midas Civil 软件对变截面连续刚构箱梁进行受力分析时，需要注意截面参数和材料参数确定、单位确定、坐标系确定3 个方面的内容。

2.3.1 截面参数和材料参数的确定

建模前应确定所用构件的截面和材料参数，准确测量所用材料的截面参数， 本模型所用材料为C50 和C40 混凝土以及Strand1860 预应力钢筋。

2.3.2 单位确定

建模前应确定合适的力学与长度的单位，本模型采用的力学单位为kN，长度单位为m，据此换算整个使用过程中的其他物理量，以避免产生数量级偏差。

2.3.3 坐标系确定

在建模过程中，车辆荷载布置时须注意局部坐标系的方向。 软件自动以整体坐标系作为车辆荷载布设的依据，为方便实际车辆布载，本模型采用选取分析跨跨中以及墩顶作为局部坐标系的原点。

3 荷载试验

根据JTG/T J21-01-2015 《公路桥梁荷载试验规程》，该变截面箱梁试验工况为边跨、中跨及墩顶的偏载和中载（表1）。 各结构跨的受力状况影响线见图3～5。

表1 荷载试验工况

图3 边跨影响线

从图3 和图4 中的影响线分布可知，荷载作用在变截面连续刚构箱梁的边跨和中跨跨中部位（边跨接近跨中）受力最大；从图5 中的影响线分布可知，荷载作用分别分布于边跨和中跨时，墩顶负弯矩受力最大。 因此，针对变截面连续刚构箱梁的影响线部分情况，设计标准活载产生的该试验项目的最不利效应值等效换算，静载试验荷载效率见表2。

图4 中跨影响线

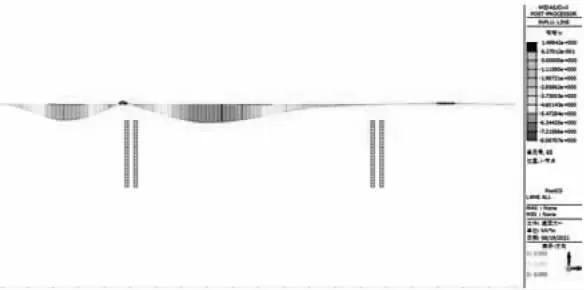
图5 墩顶影响线

表2 静力荷载试验效率

为了验证箱梁底部受力情况， 根据规范要求，在箱梁底部均匀分布6 个应力采集点（图6），其理论计算结果见表3 和图7～12。 由表3 可知，在偏载作用下，无论是边跨、中跨，还是墩顶负弯矩截面，箱梁底部6 个应变测试点，在偏载位置附近的应变测点的值均较大， 远离偏载的应变测点的值均较小；而且均成线性分布。 在中载作用下，无论是边跨、中跨，还是墩顶负弯矩截面，箱梁底部各应力测点基本相等，即各应力测点均分外荷载。 因此，箱梁所划分单元进行模拟分析是可行的，即考虑弹性变形阶段，这与设计思路基本吻合。 从理论分析结果可知，偏载对结构影响较大，特别对梁体局部受力比较明显，故在进行荷载试验时，应考虑偏载和中载试验工况，为荷载试验分析提供必要的理论依据。

表3 各测点应变理论值

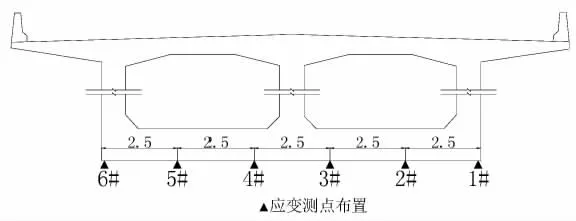
图6 箱梁底部应力采集点

根据荷载试验工况情况及应变采集点布置方式，现场采用车辆加载的方式进行荷载试验，车辆加载见图7～12。

图7 边跨跨中偏载加载车辆布置图

图8 边跨跨中中载加载车辆布置图

图9 中跨跨中偏载加载车辆布置图

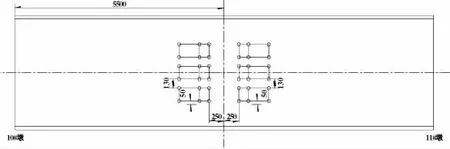
图10 中跨跨中中载加载车辆布置图

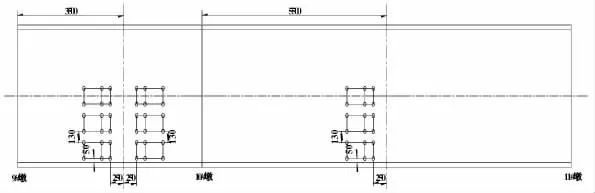
图11 墩顶偏载加载车辆布置图

图12 墩顶中载加载车辆布置图

4 结构受力分析

经过现场荷载试验，实测值和理论值对比见表4和图13～18。

根据理论计算模型结果分析，对外荷载进行试验荷载等效，其等效的外荷载作用表现为采用荷载试验车辆进行施加，具体作用点见图7～12。 由表4和图13～18 可知，荷载试验和模型计算的内力结果基本吻合，且各测点应变值与理论值线性变化较为吻合。 因此，等效作用的试验荷载可作为验证分析箱梁结构受力情况的最直接的表现，而理论计算结果可模拟分析结构受力状况，也可以为现场荷载试验提供科学的依据。

表4 各应变测点理论值与实测值对比

图13 边跨跨中偏载应变测点理论值与实测值对比

图14 边跨跨中中载应变测点理论值与实测值对比

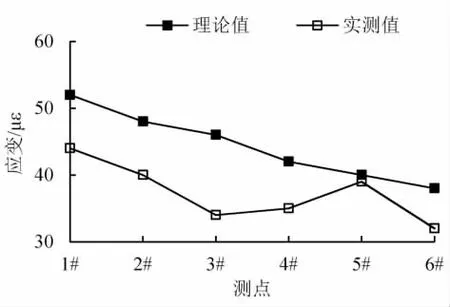
图15 中跨跨中偏载应变测点理论值与实测值对比

图16 中跨跨中中载应变测点理论值与实测值对比

图17 墩顶偏载应变测点理论值与实测值对比

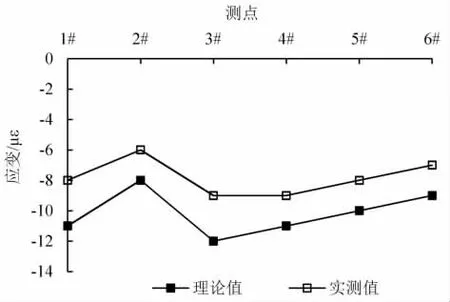
图18 墩顶中载应变测点理论值与实测值对比

综合上述对某变截面连续刚构箱梁结构的荷载试验以及结构受力分析讨论同时考虑利用Midas Civil 软件的实际建模过程，发现Midas Civil 具有如下优势：（1）利于方案优化：利用Midas Civil 模型可以方便调整车辆荷载布设具体位置。 最终选用试验荷载效率接近1.00 的位置。（2）提高计算效率：使用Midas Civil 软件验算， 克服了传统手算速度慢、计算结构单一化情况，对于变截面连续刚构箱梁这种较为复杂的结构计算效果显得尤为突出，大大提高了技术人员的工作效率。 （3）提高计算精准性：所用Midas Civil 软件提高了变截面连续箱梁计算的精准性。 如在复杂结构手算时，往往采用变形相似的方法进行变形量的计算，此时设计人员由于经验不足或者出于自身责任考虑，往往选择了较大的安全系数，进而造成资源的浪费[4]。而Midas Civil 软件所用有限元分析可有效避免该情况的发生，准确控制结构的安全性与成本。

5 结语

本研究以某项目大跨度预应力变截面连续刚构箱梁桥梁为工程背景，对其跨中截面以及墩顶截面分别进行中载和偏载的主要控制截面受力验证性研究，总结经验如下：（1）桥梁内力模拟分析采用大型有限元软件分析，但其构件转化均基于材质均匀、各向同性的假设。 实际上，桥梁各构件的材质不具备理想状态下的连续性，这就增加了桥梁结构内力分布情况的研究难度。 （2）运用Midas 有限元数值分析软件验证桥梁的内力变化情况， 以及研究桥梁处于弹性阶段时的使用情况， 所建立的变截面连续刚构箱梁有限元模型计算理论值与通过荷载试验所得桥梁结构的受力变化情况实测值趋同。（3）经过Midas Civil 建模的荷载试验实测值可知，所得等效作用试验荷载可作为验证分析变截面变截面连续刚构箱梁结构受力情况的直接手段，所得理论计算结果可为现场荷载试验提供科学的依据，也可为类似工程提供合理参考。