苹果切片热风干燥温度的优化研究
2021-02-28张大鹏贾斌广刘芳苑绍迪
张大鹏贾斌广刘芳苑绍迪
(1.山东建筑大学 热能工程学院,山东 济南250101;2.中华全国供销合作总社济南果品研究院,山东 济南250200)
0 引言
苹果作为一种产量较大的水果,其果片干制品以甜软可口、低糖、富含维生素C等特点越来越受到大众的青睐。目前,苹果切片的干燥方式主要是热风干燥的方式[1],其中以太阳能热风干燥和热泵热风干燥居多[2-3]。这种干燥方式具有稳定、可控性强等优点,但是也存在干燥时间较长、能耗较大和因干燥不均匀而产生的外壳变硬等问题[4]。因此,如何从技术角度分析、选取合适的干燥送风参数以缩短干燥时间并提高干燥的品质是亟待解决的问题。
其中,众多学者研究了果片热风干燥问题。THIJS[5]对相同体积不同形状(立方体、矩形、圆形和半圆形等)的苹果切片进行对流干燥过程的模拟,分析了不同形状的果蔬尺寸对干燥时间的影响规律,发现相同体积条件下,圆形切片干燥最快,矩形切片厚度的改变对干燥时间影响最小。DIAMANTE等[6]通过建立红薯切片热风烘干模型,分析了空气速度对红薯切片的影响规律并改进了传统红薯干燥模型,研究发现随着送风速度的增加,干燥速率加快,改进的Page方程能较好地描述甘薯片在10%干基水分条件下的薄层风干过程。HII等[7]研究了热泵热风干燥过程中可可豆干燥动力学,发现其与果核相比,在干燥的最初2 h,果皮的含水量下降相对较快,干燥结束时,果核的最终含水量高于果皮。程晶晶等[8]研究了切片厚度、装样量对苹果片热风干燥过程的影响,结果表明切片厚度、装样量均对苹果片的热风干燥过程影响较大。刘欣[9]探究了升温减湿、恒温恒湿和降温减湿度等3种送风方式对苹果片干燥时间以及品质的影响,发现降温减湿在能够保证干燥品质的同时,有效地缩短了干燥时间。目前对果蔬干燥的研究采用的主要是基于扩散模型[10],虽然模型结果与实验结果的匹配性较好,但是并不能对多孔介质内流体流动的驱动力,如毛细力等其他输运机理做出解释[11]。因此,基于果蔬的多孔介质属性,采用多相多孔介质模型MPMM(Multiphase Porous Media Models),在表征体元REV(Representative Elementary Volume)尺度下,同时考虑多孔介质中液、气相的传质以及水分蒸发相变过程,对深入研究果蔬热风干燥过程中的热湿传递情况十分有益。
目前,将MPMM应用于苹果切片干燥中的研究较少,且大多数基于实验,无法从机理上分析切片干燥过程中内部水分分布以及干燥均匀度等。因此,文章拟建立苹果切片干燥的MPMM,基于有限元法利用多物理仿真软件COMSOL Multiphysics®进行数值模拟,重点探究改变送风温度的情况下,切片内部的水分分布情况以及温度对干燥时间和干燥不均匀度的影响规律,并通过选择合适的送风温度,优化苹果热风干燥过程。
1 物理模型
考虑到薄片是苹果热风干燥中的常见形式,因此建立如下物理模型:将苹果切片放置于尺寸为150 mm×130 mm×50 mm的烘干箱体内,苹果切片的尺寸为圆柱形,其半径为20 mm、高度为5 mm。干燥模型如图1所示。
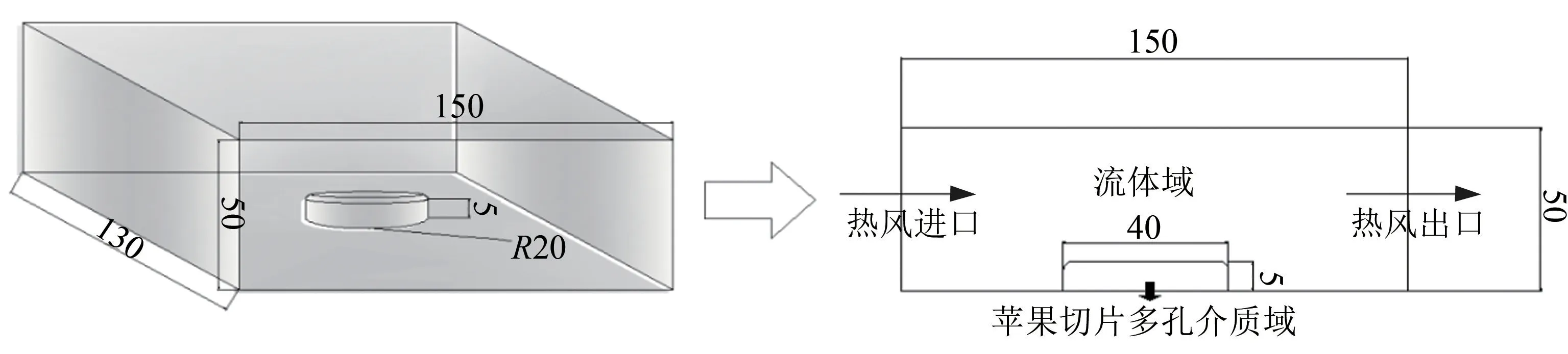
图1 苹果切片的干燥的物理模型/mm
2 数学模型
2.1 模型假设
考虑到模型的复杂性以及计算时间等要求,对模型做出如下假设:
(1)苹果切片为多孔介质,孔隙内充满3种可输运的相,即液态水、空气和水蒸气;(2)内部所有相(固体、液体和气体)分布是连续的;(3)液态水的输运是由于气压梯度、毛细管流动和蒸发产生的对流引起的,水分仅以水蒸气的方式离开切片;(4)水蒸气和空气的输送是由于气体压力梯度和水蒸气在空气中的二元扩散引起的[12]。
2.2 控制方程
控制方程由流动方程、物质输运阶段的传质守恒方程和传热方程组成。
2.2.1 流动方程
控制体内的流体流动,包括苹果切片外侧的干燥空气在流道内的流动,以及湿空气在被干燥的苹果切片多孔介质内的流动。流道内流体流动和切片内水蒸气的流动均为层流流动,用传统的纳维—斯托克斯方程(Navier-Stokes equtions)计算。连续性方程和动量方程[13]分别由式(1)和(2)表示为
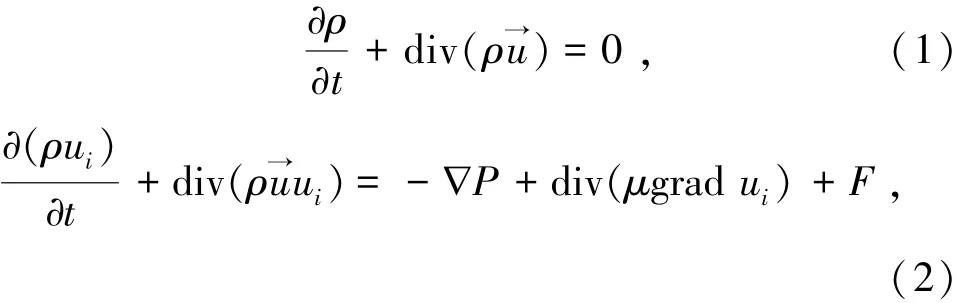
式中ρ为流道内流体的密度,kg/m3;u→为流体在x、y、z方向上的方向向量;ui为流体在x、y、z方向上的方向速度,m/s;P为流动压力,Pa;μ为流体的动力黏度,Pa·m;F为体积力项,F=ρg(g为重力加速度)。
在干燥的苹果切片(多孔介质)内,根据Brinkman方程求解切片内部的压力和速度由式(3)和(4)表示为
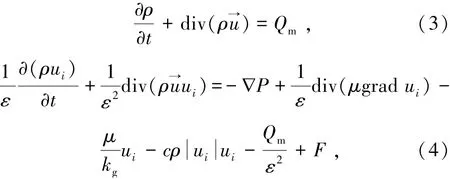
式中Qm为质量源,kg/(m3·s);c为常数,通常取0.6;ε为孔隙中气相所占的份数,ε=φSg;kg为气相渗透率。
2.2.2 质量守恒方程
水的质量浓度cl、蒸汽的质量浓度cv和空气的质量浓度ca分别由式(5)~(7)表示为
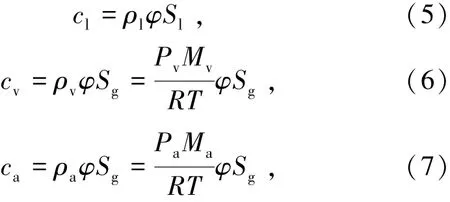
式中cl、cv、ca分别为水、蒸汽和空气质量浓度,kg/m3;ρl为水的密度,kg/m3;R为通用气体常数,J/(mol·K);T为干燥切片温度,K;Pv为蒸气分压,Pa;Pa为空气分压,Pa;Ma和Mv分别为空气和水蒸气的摩尔质量,kg/mol;φ为孔隙率;而液相饱和度Sl、气相饱和度Sg可以由式(8)和(9)表示为
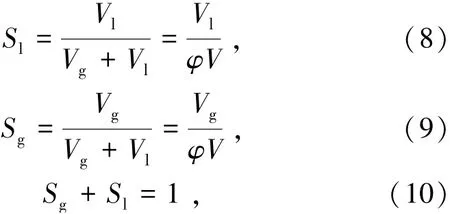
式中Vl和Vg分别为孔隙中液相和气相所占的体积,m3;V为孔隙总体积,m3。
液态水的质量守恒方程由式(11)表示为
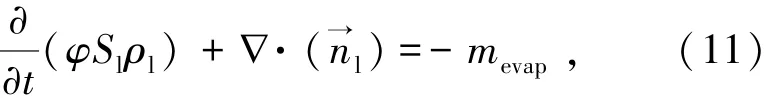
mevap与水蒸发饱和蒸气压有关,由式(12)表示为
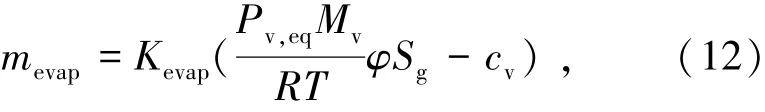
式中Pv,eq为水蒸气的平衡压力,Pa;Mv为水蒸气的摩尔质量,kg/mol;R为气体常数,J/(mol·K);T为温度,K。
根据达西定律[14],液态水的总流动是由于液体压力梯度(Pl=P-Pc)引起的,由式(13)表示为
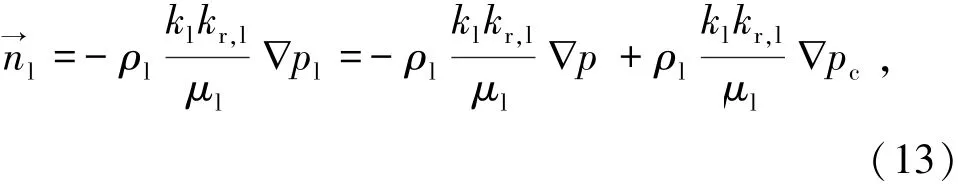
式中P为总气体压力,Pa;Pc为毛细管压力,Pa;kl为水的固有渗透率,m2;kr,l为水的相对渗透率;μl为水的动力黏度,Pa·s。
而毛细管压力Pc取决于特定材料的浓度cl和温度T,由温度梯度∇T引起的毛细管扩散系数被称为索瑞特效应(Soret effects),与浓度梯度扩散引起的扩散系数相比[15],经常被忽略。因此,液态水的传质方程可由式(14)表示为
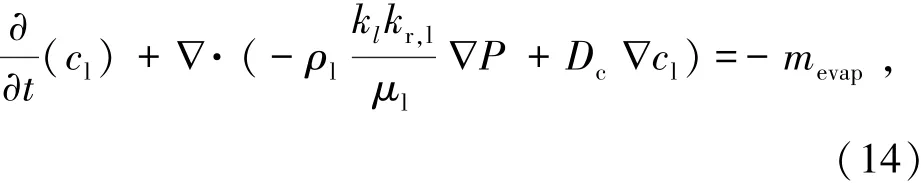
水蒸气的传质守恒方程由式(15)表示为
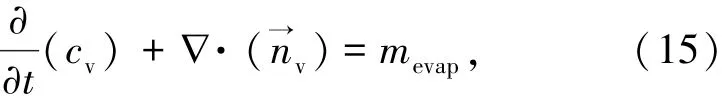
式中n→v为水蒸气的传递通量,kg/(m2·s);mevap为水的蒸发量,kg/(m3·s)。
根据HALDER等[16]提出的多孔介质中水蒸气传递通量表达式,n→v由式(16)表示为
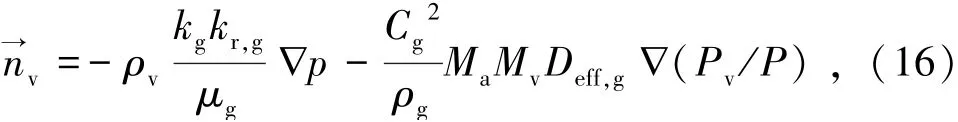
式中kg、kr,g分别为气体的固有渗透率和相对渗透率,m2;ρg为气相的密度,kg/m3;μg为气体的黏度,Pa·s;Pv/P为水蒸气的平衡蒸气压与总压力之比。在切片多孔介质之外的空气域内,水蒸气在空气中的扩散方程由式(17)表示为

2.2.3 能量守恒方程
空气域内的能量守恒方程由式(18)表示为

式中ρma为流道内气相的密度,kg/m2;cp,ma为流道内气相的比热容,J/(kg·K);u为流道内气相的流速,m/s;kma为流道内气相的导热系数,W/(m·K);hfg为水的汽化潜热,J/kg。
干燥切片多孔介质区域的能量守恒方程[17]由式(19)和(20)表示为
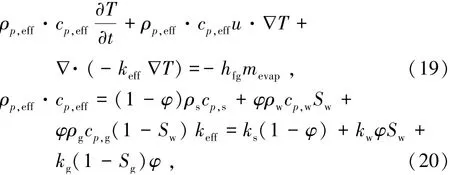
式中ρp,eff为有效密度,kg/m3;cp,eff为有效比热容,J/(kg·K)。通过式(20)计算得出,其与多孔介质中各组分所占比有关;keff为有效热导率,W/(m·K);ρs、ρw、ρg分别为多孔介质中固体、液相、气相的密度,kg/m3;cp,s、cp,w、cp,g分别为多孔介质中固体、液相、气相比热容,J/(kg·K);ks、kw、kg分别为多孔介质中固体、液相、气相的热导率,W/(m·K)。
2.3 主要评价指标
2.3.1 含水率
由于湿基含水率的范围在0~1,为了计量方便,苹果切片干燥的含水率主要是通过湿基含水率来计算的。湿基含水率Mwb为被干燥物体中的水分含量与总质量的比值[18],由式(21)表示为

式中φ为孔隙率;Sl为液相饱和度;ρl为水的密度,kg/m3;ρl为固相的密度,kg/m3。
2.3.2 干燥不均匀度
干燥过程中不均匀度主要包括温度不均匀度和含水率的不均匀度。为了衡量送风温度对苹果切片干燥均匀性的影响,基于文献[19]的计算方法得到热风干燥过程中的温度和含水率的不均匀度。
温度、含水率不均匀度的计算分别由式(22)和(23)表示为

式中δx为温度/含水率不均匀度为平均的温度/含水率;n为测点数;xi为测点温度/含水率(当x为t时,表示温度不均匀度;当x为w时,表示含水率不均匀度)。
2.4 初始及边界条件
初始条件:对于空气域,初始相对湿度20%,初始温度T为20℃;对于切片多孔介质区域,其初始含水率0.848,初始水蒸气含量cv为0.17 kg/m3,初始温度T为20℃。边界条件:入口速度为1 m/s,入口温度分别为40、45、50、55、60、65℃,送风相对湿度20%。出口边界:压力出口。除干燥进出风口外,其它均为绝热边界。
2.5 网格划分
基于COMSOL软件自定义网格划分选项,采用非结构化网格对模型进行网格划分,如图2所示,计算网格数为69万。由于涉及切片表面水分蒸发,因此对苹果切片表面进行网格加密,如图3所示。

图2 模型网格划分示意图

图3 切片表面处网格划分示意图
3 结果与分析
3.1 实验验证
选取新鲜的红富士苹果为实验样品,在使用之前保存在(5±1)℃的冷藏室中,以保持尽可能新鲜。从储藏库中取出苹果,清洗并静置1 h,使其温度在每次干燥实验前升至室温;将样品切成厚度为5 mm、直径约为40 mm的圆形切片,放入热风干燥箱内,将温度设置为50℃、风速为1 m/s、送风相对湿度为20%。每次干燥测试完后,将切片样品加热至100℃并持续至少24 h,得到切片固体基质质量,计算出苹果片的初始水分含量约为0.848。水分损失记录在定期间隔1 h,通过高精度数字天平进行称重。进行3次实验,并计算出标准偏差。实验结果与模拟验证如图4所示,模拟结果和实验结果变化趋势一致,且模拟误差较小,绝对误差<8%,因此模拟结果是可信的。
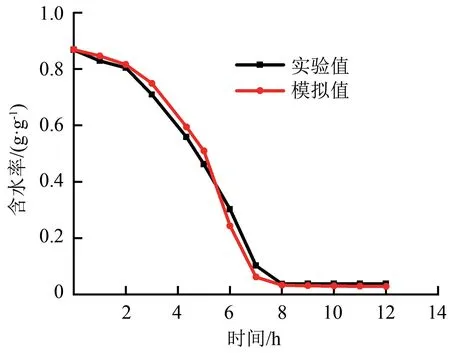
图4 苹果切片含水率的实验与模拟验证图
3.2 送风温度对切片含水率分布的影响
不同温度下,干燥5 h时切片中心处的水分分布情况如图5所示。可以看出,在相同的风速下,随着干燥送风温度的升高,干燥速率加快,等含水率线向内侧区域向移动。40℃时,由于送风温度较低,热风受到切片前端阻碍且前后端接触热风存在时间差,切片前端上侧位置含水率首先减少,但是此时切片内部含水量仍然较高,含水区域面积较大。随着温度的增加,干燥速率加快,切片前端含水率较低的区域逐渐扩大。当送风温度增加至65℃时,切片内部水分含率较高的区域已经收缩至切片内部的某一区域。因此,在相同的送风速度和相对湿度下,同一干燥时刻,送风温度越高,干燥含水率减少的越快,越有利于干燥;但温度越高,切片内部含水率差异也越大,内部水分越不均匀。
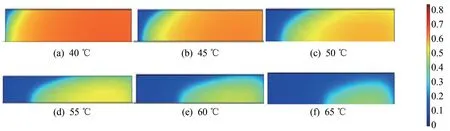
图5 不同温度下干燥5 h时切片中心处内部含水率分布图
3.3 送风温度对干燥时间的影响
送风速度为1 m/s、送风相对湿度为20%,送风温度分别为40、45、50、55、60、65℃的条件下,苹果切片的含水率变化曲线如图6所示。不同温度下切片含水率的变化趋势基本一致,皆是由缓至快,最后趋于稳定的趋势。且随着干燥送风温度的增加,干燥含水率达到稳定所需要的时间也越少。

图6 不同温度下切片的含水率变化曲线图
由于无法直接定量地比较干燥曲线(质量损失与时间)的差异,根据DEFRAEYE[20]的实验结果,定义苹果切片干燥湿基含水率达到0.12时所需要的时间为干燥所需时间,其与温度的关系如图7所示。可以看出,随着送风温度的增加,所需干燥时间降低。原因是随着温度的升高,热风与干燥切片之间的水蒸气压力差增大,使苹果切片内部水分能更快速的蒸发[21],从而缩短了干燥时间。因此,提高干燥送风温度是减少干燥时间的重要手段。同时,对干燥时间变化曲线进行拟合发现,干燥时间随着温度变化是一条向下递减并趋于稳定的二次函数曲线(拟合精度0.996),即表明所需干燥时间随干燥温度的变化逐渐趋于稳定,不能通过无限提高送风温度来降低干燥时间。
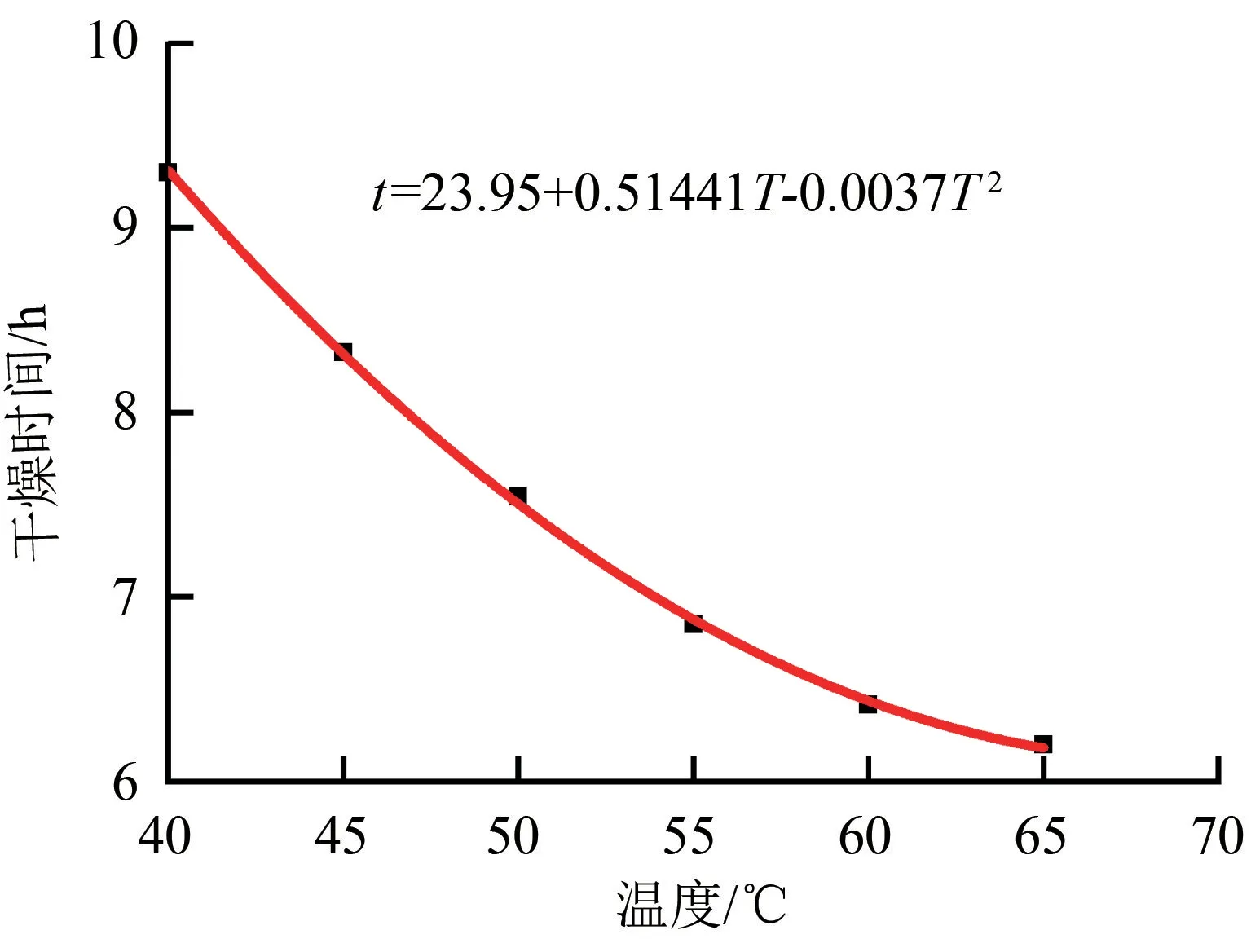
图7 不同送风温度下所需的干燥时间图
3.4 送风温度对干燥均匀性的影响
不均匀度是反映干燥过程中温度或者含水率分布均匀程度的物理量[22],送风温度对干燥均匀程度有着较大的影响。不均匀度过大可能导致切片发生干裂,使其表面变硬、复水性变差,影响干制品口感和品质。为了不均匀度分析的准确性,选取的切片内数据点分布位置如图8所示,每层13个,3层共39个数据点。在导出干燥过程中这些数据点的温度和含水率的变化数值后,通过式(22)和(23)计算切片整体在干燥过程中的不均匀度。

图8 切片选取测点位置图
由于送风温度不同,因此所需干燥时间也不同。以干燥至含水率为0.12的时间为干燥截至时间,干燥过程中切片的温度不均匀度和湿度不均匀度随时间变化如图9所示。可以看出,温度和湿度的不均匀度变化趋势一致,都是一个由平缓到快速上升又急速下降的曲线,干燥的不均匀度较高的时刻主要出现在干燥后期。造成这种变化的主要原因是因为干燥过程中热量的变化主要包含显热和潜热部分,在干燥初始时刻,干燥的热量一部分用于提高潜热,另一部分提高切片内部的显热,由于切片内部含水率较高且水的比热容较大,因此干燥前期温度和含水率梯度并不明显,整体的温度和含水率不均匀度较低。随着干燥向内部进行,切片内外温度梯度和含水率梯度增大,不均匀性也逐渐增大。进入干燥后期,整体含水率已经较小,此时水分分布对温度和含水率的影响已经较小,因此温度和含水率不均匀度开始降低。
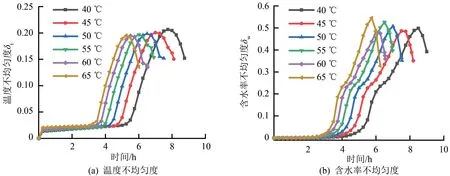
图9 不同温度下切片温度不均匀度、含水率不均匀度随时间的变化图
温度不均匀度和湿度不均匀度是干燥品质的两个评价指标,为了探究苹果切片干燥过程中两者是否存在线性关系式,基于40、50、60℃时不均匀度变化曲线,利用Origin进行公式拟合,得到的拟合曲线如图10所示。
不同温度下,温度和湿度不均匀度的拟合函数由式(24)表示为

式中δt为温度不均匀度;δw为含水率不均匀度。当送风温度为40℃时,A=0.3810、B=0.0057,拟合精度为0.960;送风温度为50℃时,A=0.3752、B=0.0040,拟合精度为0.971;送风温度为60℃时,A=0.3644、B=0.0014,拟合精度为0.967。
通过对40、50、60℃送风温度下的温度不均匀度和含水率不均匀度进行分析发现,干燥过程中温度不均匀度和含水率不均匀度是线性关系。因此,在以后的分析当中,可以通过计算干燥过程中含水率的不均匀度反映出温度的不均匀度,平均含水率不均匀度计算式由式(25)表示为

式中εw为平均含水率不均匀度;t为干燥时间;εi,t为不同温度下的含水率不均匀度变化曲线(其中i为含水率不均匀度曲线;t为对应的时间)。
结合式25,对5种送风温度下切片的含水率不均匀度随时间的变化进行积分运算再除以总干燥时间,得出干燥过程中切片内部总的含水率不均匀度平均值,结果如图11所示。可以看出,拟合曲线是一条向上递增并趋于稳定的二次函数曲线(拟合精度0.993),表明切片的平均含水率不均匀度是一个先上升后平缓的过程。也就是说,干燥温度越低,不均匀度越低,干燥越均匀;其温度越高,不均匀度增加,干燥越不均匀。当送风温度较高时,干燥送风温度对含水率不均匀度的影响已经逐渐减小。

图10 不同送风温度下切片的温度、含水率不均匀度拟合曲线图
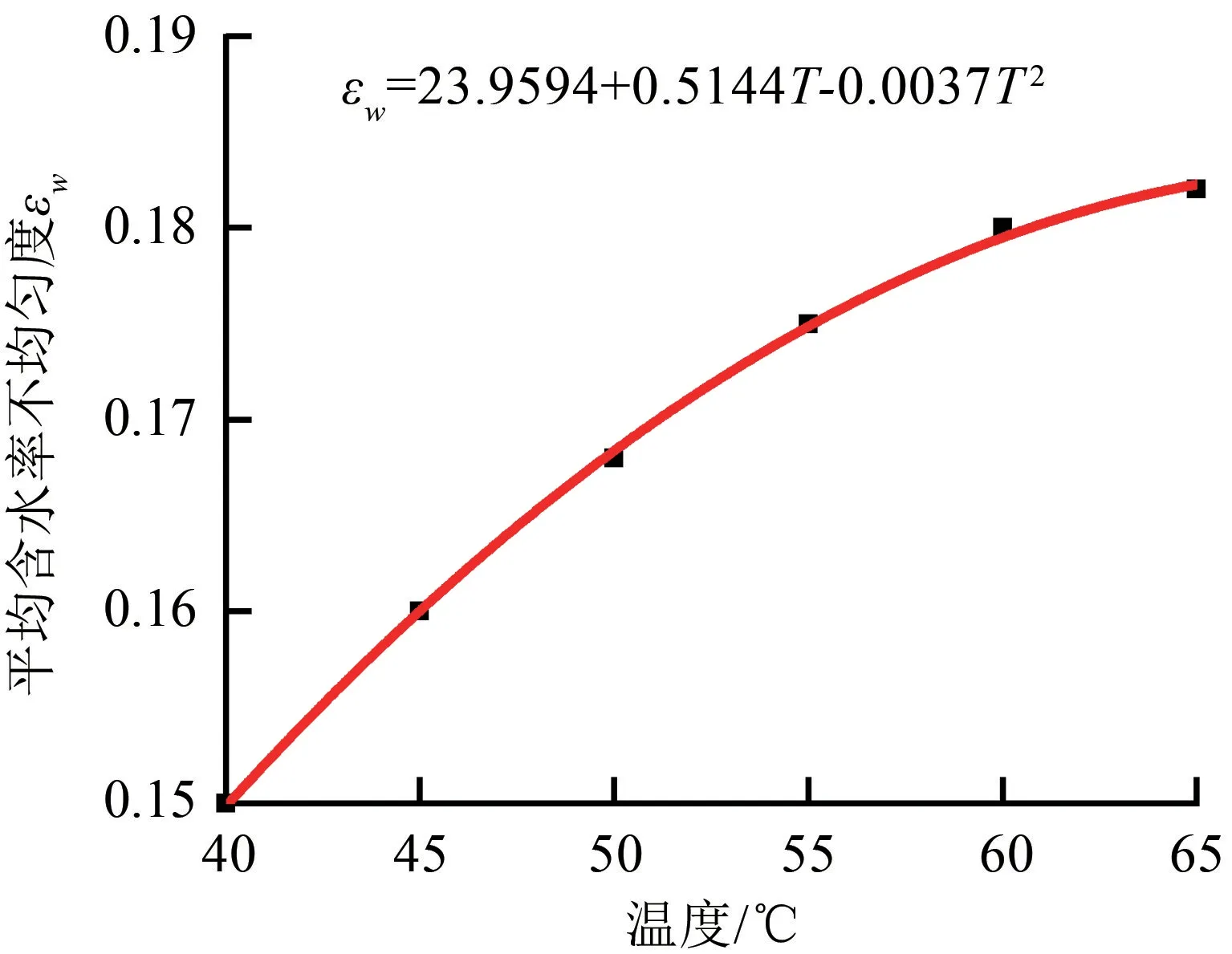
图11 不同温度下切片平均含水率不均匀度图
3.5 热风干燥最佳温度的确定
干燥温度的提高能够缩短干燥时间,提高干燥效率,但是同样会使得切片平均含水率不均匀度的增加,进而会使得切片表面开裂、硬化。因此,除了考虑缩短干燥时间外,还应该综合分析不同温度下切片的干燥时间和平均含水率不均匀度。
不同温度下切片的平均含水率不均匀度和干燥时间对比如图12所示。在干燥送风温度为50℃附近时,两者有一个交点,因此为了使得切片的含水率不均匀度不至于过大而使切片干裂,同时又能缩短干燥时间,选择送风温度为50℃。
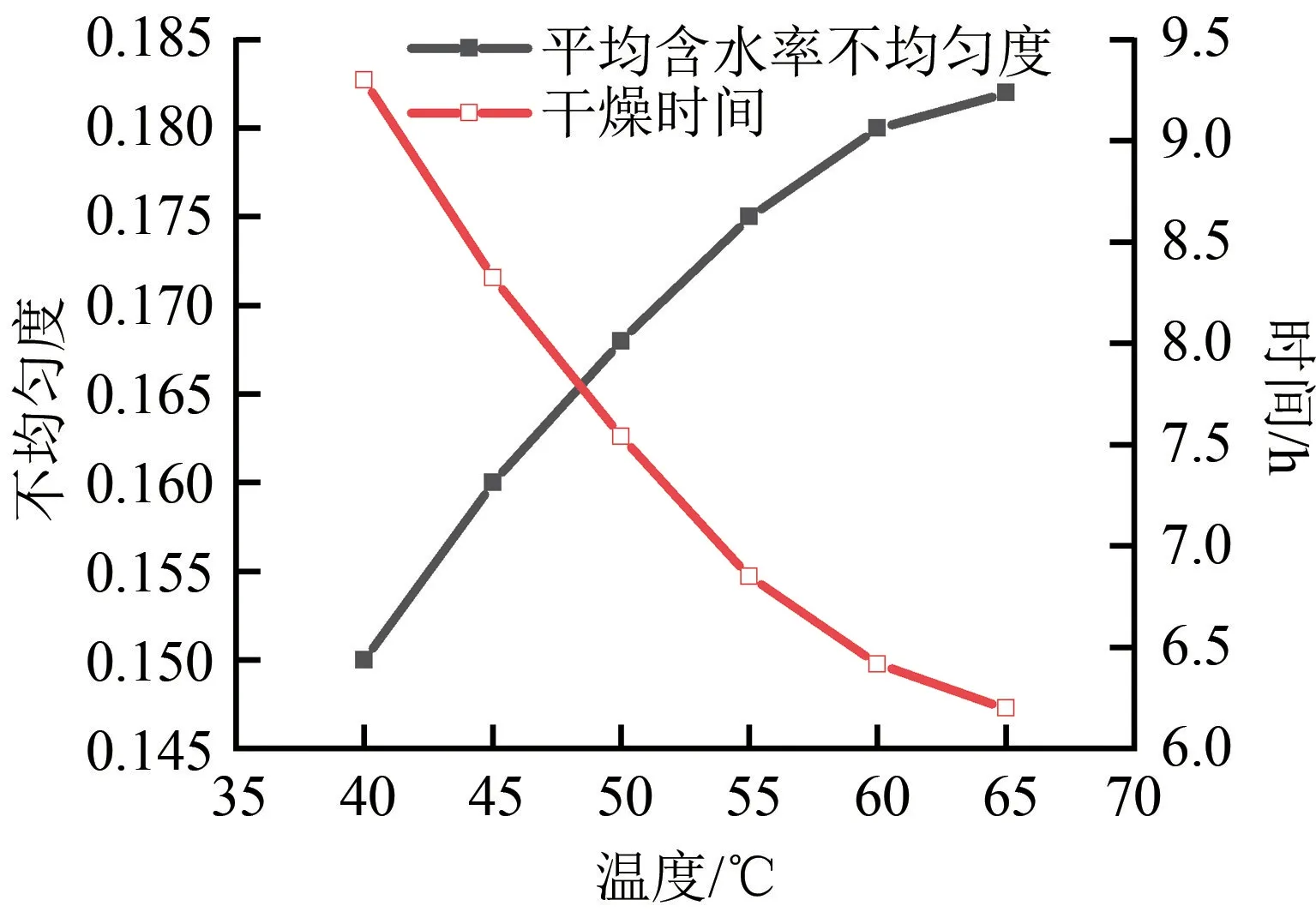
图12 不同温度下切片的平均含水率不均匀度和干燥时间对比图
4 结论
通过分析热风干燥过程中不同送风温度(40、45、50、55、60、65℃)下的苹果切片的含水量与不均匀度的变化,得出以下结论:
(1)送风温度越高,切片含水量减少的越快,干燥所需时间也相应的缩短,通过对干燥时间拟合发现,其满足二次函数关系式。
(2)随着送风温度的增加,温度不均匀度和含水率不均匀度呈上升的趋势,通过函数拟合发现,两者呈一次函数关系,因此温度和含水率不均匀的变化能够相互反映,且送风温度的增加同样会使得平均含水率不均匀度增大。
(3)综合分析不同温度下的切片干燥时间、干燥过程中的平均含水率不均匀度,为保证含水率不均匀度不至于过高而使得切片干裂,同时又能缩短干燥时间,选择送风温度为50℃。
