模糊测试变异算子调度优化模型

2021-02-28李明磊陆余良朱凯龙

小型微型计算机系统 2021年10期

李明磊，陆余良，黄晖，朱凯龙

(国防科技大学电子对抗学院，合肥 230037) (网络空间安全态势感知与评估安徽省重点实验室，合肥 230037)

1 背景

模糊测试技术是一种通过随机输入对程序进行测试的技术.研究人员通过分析程序崩溃时的程序上下文状态与输入的测试用例实现对程序漏洞的定位[1].模糊测试技术因其自动化程度高、软件适用性好等优点被广泛应用于软件测试当中.为提高模糊测试技术的效率，研究人员对模糊测试技术开展了广泛的研究，将静态分析、污点分析、符号执行等技术引入到模糊测试技术中，使得模糊测试技术可以通过收集程序运行状态指导测试用例的生成，出现了以AFL[2]、Driller[3]、AflFast[4]、Skyfire[5]、BORG[6]为代表的反馈式模糊测试器.

当前模糊测试技术有基于变异和基于语义的两种测试用例生成方法[7].基于变异的测试用例生成方法指模糊测试器对测试用例进行随机变化，产生新的程序输入作为测试用例，每一种随机变化方式称为一种变异算子，基于变异生成测试用例的模糊测试器有AFL、AflFast、Peach[8]、EcoFuzz[9]等.基于语义的测试用例生成方法指模糊测试器对程序输入的语义进行分析得到程序输入的格式，模糊测试器在程序输入格式的指导下生成测试用例，基于语义生成测试用例的模糊测试器有SPIKE[10]、Learn & Fuzz[11]等.

无论是基于变异还是基于语义的测试用例生成方法都只关注单一变异算子本身的变异效率，在实际测试过程中模糊测试器会同时调用多种变异算子生成测试用例.面对同时调用多种变异算子的情况时，当前模糊测试技术认为不同变异算子变异效率相同，不考虑不同程序状态对不同变异算子的影响，简单地通过固定顺序或随机调度方式选择变异算子，造成模糊测试器性能的浪费.

本文对不同变异算子之间的协同调度问题进行研究，首先通过大量实验，分析不同变异算子在不同程序状态下的变异效率，为建立变异算子调度模型提供数据支撑，其次根据实验数据以探索利用模型为基础，建立变异算子调用优化模型EE-POS，并基于开源项目AFL实现了EE-POS-AFL.

2 相关研究

在本节中以开源模糊测试器AFL为例，对变异算子的变异效率进行研究，表1为AFL中用到的变异算子[12].AFL通过固定顺序与随机调度相结合的策略对变异算子进行调度.当测试用例进行第1轮变异时，AFL按照固定顺序依次调用表1中的变异算子生成测试用例，当该测试用例进行第2轮变异时，AFL随机调用表1中的几种变异算子进行组合生成测试用例.这种变异调度方式虽然简单快捷，但会产生大量的无效变异，无法保证模糊测试器整体变异效率最优.

表1 变异算子

为进一步解释随机调度变异算子无法保证模糊测试整体效率最优的原因，本文使用AFL分别对命令处理类软件Objdump、图像处理类软件Tiff和流媒体软件Libming进行持续一周的测试，统计不同变异算子调用的次数与该变异算子产生的有效测试用例的数量，本文中有效测试用例指该测试用例覆盖到了程序新的路径.表2统计了AFL持续运行7天后，不同变异算子被调用的次数与产生的有效测试用例数量.Exe表示变异算子选用了几次，单位兆次.Num表示变异算子产生的有效测试用例的数量.

表2 变异算子调用产出表

为便于分析对表2数据进行处理，处理后的数据如图1、图2、图3所示.图1为Libming变异效率比例图，图2为Objdump变异效率比例图，图3为Tiff变异效率比例图.图中横坐标为模糊测试器调用的变异算子，纵坐标分别为该变异被调用的次数在总调用次数中的占比(左侧有填充条柱)和该变异算子产生的有效测试用例在有效测试用例总体中的占比(右侧无填充条柱).

图1 Libming 变异效率比例图

从图1、图2、图3可以看出，不同变异算子在不同类型的程序上的变异效率不同，以变异算子Arith8/8为例，在Libming中以19.2%的调用比生成了32.9%的有效测试用例；在Objdump中以19.1%的调用比生成了18.8%的有效测试用例；在Tiff中以4.7%的调用比生成了25.4%的有效测试用例.

图1、图2、图3对同一个变异算子在不同程序上的变异效率进行了研究，接下来对同一个变异算子在一个程序不同时刻的变异效率展开研究，为便于展示从15个变异算子中选取4个变异算子进行跟踪分析.分析结果如图4、图5、图6所示.图4为Libming变异效率变化曲线，图5为Tiff变异效率变化曲线，图6为Objdump变异效率变化曲线.

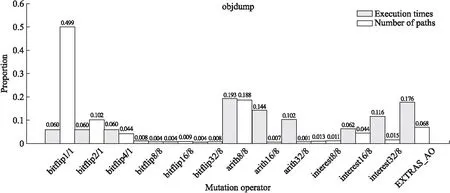
图2 Objdump 变异效率比例图

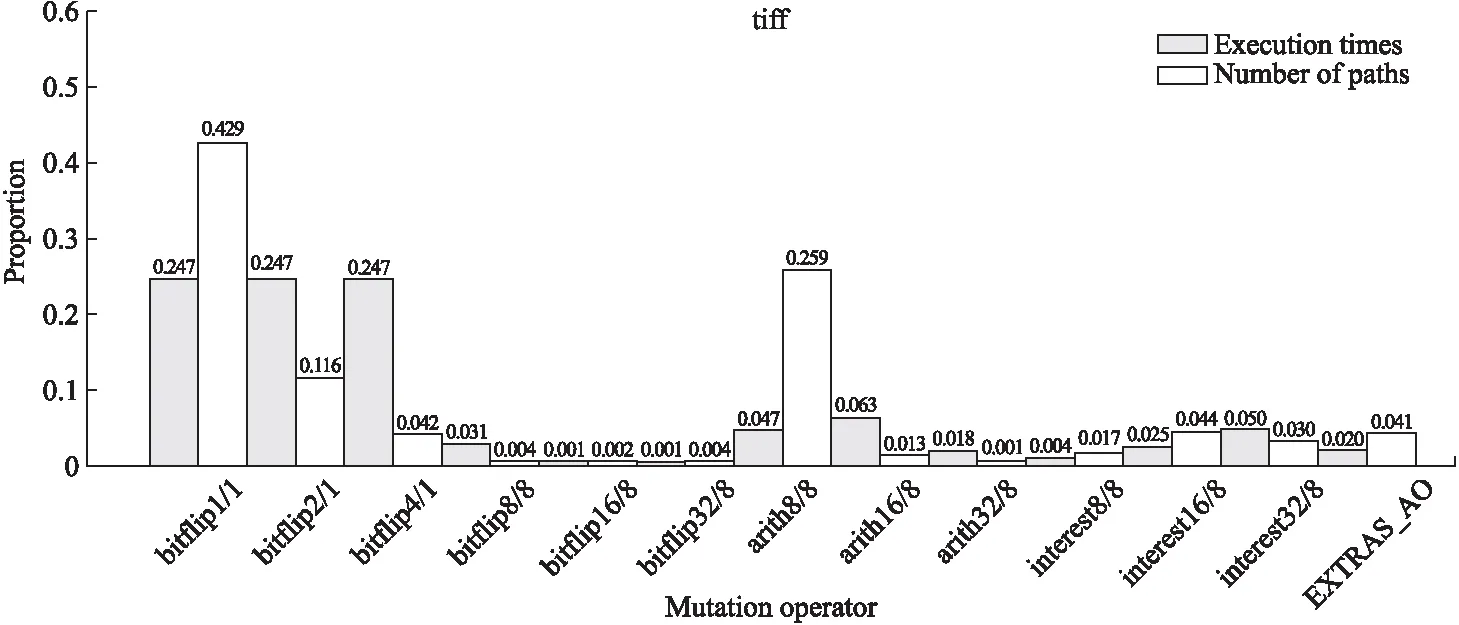
图3 Tiff 变异效率比例

在图4、图5、图6的变化中可以看到，随着时间的变化不同变异算子的变异效率在动态变化.以变异算子Arith8/8为例，在对测试程序Libming进行测试的过程中，Arith8/8在0到960分钟内的变异效率要高于960分钟到2880分钟内的变异效率.此外，通过图4、图5、图6的变化变化趋势可以看出，每个变异算子的变异效率具有收敛性，从实验数据可以得出以下4个结论：

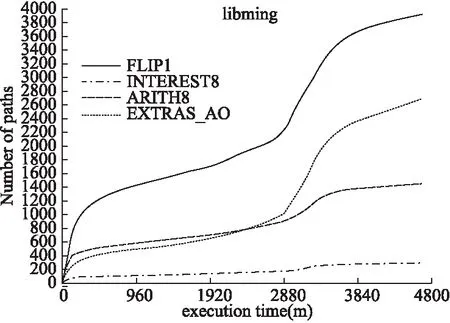
图4 Libming 变异效率变化曲线

图5 Tiff 变异效率变化曲线

图6 Objdump 变异效率变化曲线

1)同一变异算子在不同程序上变异效率不同.

2)同一变异算子在同一程序上不同时刻的变异效率不同.

3)随着变异算子调用次数的增多，该变异算子变异效率逐渐降低.

4)随着变异算子调用次数的增多，不同变异算子之间发现的路径数量比例趋于稳定.

基于以上4点结论，可以看出随机或固定顺序的变异算子调度策略无法使模糊测试器对所有类型的程序都保持一个较高的变异效率.合理的变异算子调度策略应该满足适应不同程序、适应不同时刻和资源占用低3个特性.具体来讲，一个合理的变异调度策略可以花费极少的资源对当前变异算子的变异效率进行统计，并根据变异算子的变异效率进行变异调度，使得模糊测试器始终保持一个较高的变异效率.

3 变异算子优化模型

3.1 探索与利用模型

探索与利用模型是一种通用的强化学习模型，常被用来解决在有限次尝试中获取最大收益类的问题，以多臂老虎机问题对该模型解决的问题进行简要介绍[13].假设当前有k个老虎机，每个老虎机会以一定概率吐出金币，如何在n次的选择中获取最多的收益是探索与利用模型所解决的问题.

在多臂老虎机问题中，每个老虎机吐出金币的概率未知.在进行选择前需要先对每个老虎机进行一定次的选取，以估算每个老虎机吐出金币的概率，之后根据不同老虎机吐出金币的概率对老虎机进行选择.估算老虎机吐出金币概率的过程称为探索，根据概率进行老虎机选取的过程称为利用.

在变异调度问题中，变异算子之间无相互干扰，每个变异算子可以类比为一台老虎机，变异调度问题可以转化为探索与利用问题进行解决.但与理想情况下的老虎机问题不同，变异算子得到有效测试用例的概率是动态变化的.因此，需要对利用阶段变异算子发现有效测试用例的概率进行动态更新.

基于探索利用模型并结合第2章对变异算子变异效率的分析，可以得到变异调度优化模型应满足的3条原则.

1)在利用阶段动态更新变异算子发现有效测试用例的概率.

2)变异算子整体发现有效测试用例概率最高.

3)在利用阶段保持一定比例的探索.

3.2 变异算子调度优化模型

在3.1节讨论了变异算子优化模型设计的3条原则.在本节中对变异算子调度优化模型进行设计.首先给出变异算子优化模型的优化目标函数，如公式(1)所示.

(1)

公式(1)中X表示变异算子被选中的总次数，Pi表示第i个变异算子生成有效测试用例的概率，xi表示第i个变异算子被选中的次数.F(X)为优化目标，求解该问题的关键在于为变异算子i分配合理的选择次数，使得模糊测试器在有限次变异中发现更多的路径.这类问题最简单的做法是将所有选择次数都分配给Pi最大的变异算子.但在变异算子优化模型中Pi为估计值，该值在模型初期误差较大，将所有的选择次数都分配给Pi最大的变异算子将会引入较大的误差.此外，Pi的值随时间动态变化，变异算子优化模型需要具备对Pi进行定期更新的能力.这就要求在利用阶段每个变异算子都应被分配到一定比例的选择次数.因此每个变异算子被选中的次数必须大于0.

在变异算子优化模型中，将采取按比例分配的方式为每个变异算子分配执行次数，如公式(2)所示.公式中R表示Pi更新的轮次，C表示Pi在R次更新和R+1次更新之间，模糊测试器选择变异算子的总次数.

(2)

通过按比例分配执行次数的方式，将每个变异算子的执行次数与其生成有效测试用例的概率挂钩，这样可以将探索过程与利用过程相结合.在模型初始化阶段给每一个变异算子赋予相同的概率，可以使得每个变异算子得到相同的执行次数，此时模型以探索为主.随着模型不断更新，不同变异算子之间的概率差异变大，每个模型分配到的执行次数随着产生分化，此时模型以利用为主.

(3)

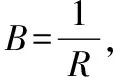
(4)

在得到了Pi更新函数后，对Pi更新周期进行研究.从图4、图5、图6可以看出变异算子的变异效率在测试初期波动较大，随着模糊测试的不断进行，变异算子的变异效率趋于稳定.因此，Pi在变异效率波动较大时应快速更新，在变异效率趋于稳定时应降低更新频率，以降低模型更新带来的资源开销.在模型中引入扰动系数F描述每次更新Pi后模型波动的大小，如公式(5)所示.在模型运行过程中通过扰动系数F对每轮测试的时长进行控制，扰动系数越大模型波动越剧烈，模型应该提高Pi更新速度.

(5)

3.3 模型实现

在3.2节中给出了模型的关键函数，在本节中对模型的实现进行介绍.变异调度优化模型分为3个模块：初始化模块、探索与利用模块、概率更新模块.在初始化模块中对模型中的数据结构进行优化，为每个变异算子赋予初始概率.探索与利用模块按照变异算子生成有效测试用例的概率为每个变异算子分配选择次数，调用模糊测试器中的变异操作对程序进行测试并收集反馈信息.概率更新模块根据探索与利用模块收集到的反馈信息计算变异算子生成有效测试用例的概率和模型波动系数，模型运行过程如算法1所示.

算法输入为每轮测试选择次数Limit，变异算子初始化概率Init[i]，模型波动系数F，变异算子个数.算法输出为变异算子发现的有效测试用例集.

算法1.变异调度优化算法

输入：Limit，Init[i]，F，Op，TestCaseSet

输出：EffectiveCaseSet

1. P[i]=Init[i]

2. F=1

3. C=0

4. X[i]=0

5. f[i]=0

6. While(Stop)//是否收到终止信号

8. {tmp=Calculation_score()

9. C=C+tmp

10. X[i]=Distribution(tmp，P[i])

11. Fuzz(X[i]，f[i])

12. }

13. P[i]=Update_efficiency(X[i]，f[i])

14. F=Calculate_fluctuation(X[i]，f[i])

15. f[i]=0

16. C=0

17.}

算法1到5行为模型的初始化模块，执行初始化操作，为模型中的数据结构赋初始值.

算法第6到第12行为模型的探索利用模块，算法第6行判断模糊测试是否接收到终止信号，算法第7行判断当前更新轮次执行次数是否小于当前更新轮次限定的执行次数，小于则继续执行本轮次更新，大于则对变异算子发现有效测试用例的概率进行更新.算法第8行调用模糊测试器中的Calculation_score函数，该函数从测试用例集中选择一个测试用例计算该测试用例需要进行变异的总次数.算法第10行按照公式2为每个变异算子分配选择次数.算法第11行调用模糊测试器中的fuzz函数，该函数按照分配好的变异次数调用不同的变异算子对测试用例进行变异，统计每个变异算子生成的有效测试用例数量，并将产生的有效测试用例加入到输出集合中.

算法13到16行为模型更新概率更新模块，算法13行按照公式(3)、公式(4)更新变异算子发现有效测试用例的概率.算法14行按照公式(5)计算模型的波动系数.

3.4 模型效率分析

为说明变异算子调度优化模型对模糊测试器运行效率的影响，从时间复杂度和空间复杂度两个方面进行分析.

首先对空间复杂度进行分析，在变异调度优化模型中共引入了4个n维数组(n为变异算子的数量)记录变异算子的初始变异效率、被选中次数、有效变异次数等信息，产生的额外空间开销为O(n).

4 实验

为了检验变异算子调度优化模型的效果，本文在开源项目AFL基础上实现了EE-POS-AFL，并与AFL进行对比实验.实验对模糊测试器路径发现效率、Crash发现效率两个指标进行对比.测试程序分为两类，一类为真实目标程序Libming、Tiff和Objdump；第2类为模糊测试器通用测试集LAVA-M[14]中的Who、Base64、Md5sum和Uniq.

实验服务器设置为：Intel(R)Xeon(R)Gold 6230×4，252G内存，8T固态硬盘，操作系统为Unbuntu server 20.04.

Libming、Tiff和Objdump初始测试用例为选取自Testsuite测试集，Who、Base64、Md5sum和Uniq初始测试用例选取自LAVA-M自带的初始化种子.实验持续进行7天，进行5次重复实验，实验结果取平均值.实验结果如表3所示，表中Path测试器覆盖到的路径数量，Crash表示模糊测试器生成的可以使程序奔溃的测试用例.

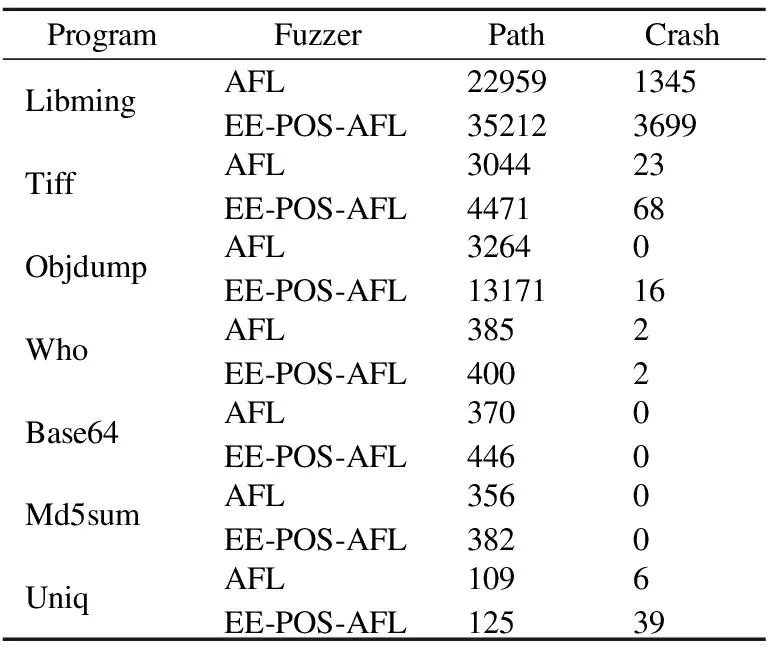
表3 实验结果统计

为便于分析对表3的数据进行处理生成效率对比表，如表4所示.表中Improve_p表示EE-POS-AFL与AFL相比发现的路径总数提高的倍数.表4中Improve_c表示EE-POS-AFL与AFL相比发现的Crash总数提高的倍数.

表4 效率对比表

从表4可以看出相比AFL，EE-POS-AFL在路径发现数量和Crash发现数量上都有明显的提升，在实际应用程序上提升更为明显.在Objdump上路径发现数量提升了4.03倍，Crash发现数量提升16倍.在Who、Md5sum两个测试程序上EE-POS-AFL效果提升并不明显.通过对初始测试用例的分析，发现Who、Md5sum的初始测试用例较小，经过长时间的模糊测试已经无法生成有效的测试用例使得程序覆盖到新的路径.为更进一步对AFL与EE-POS-AFL的效率进行比较，将Who和Md5sum的路径发现数量与时间之间的关系绘制成图像，如图7、图8所示.图7为Md5sum路径发现数量随时间变化图，图8为Who路径发现数量随时间变化图AFL.

图7 Md5sum 路径发现数量

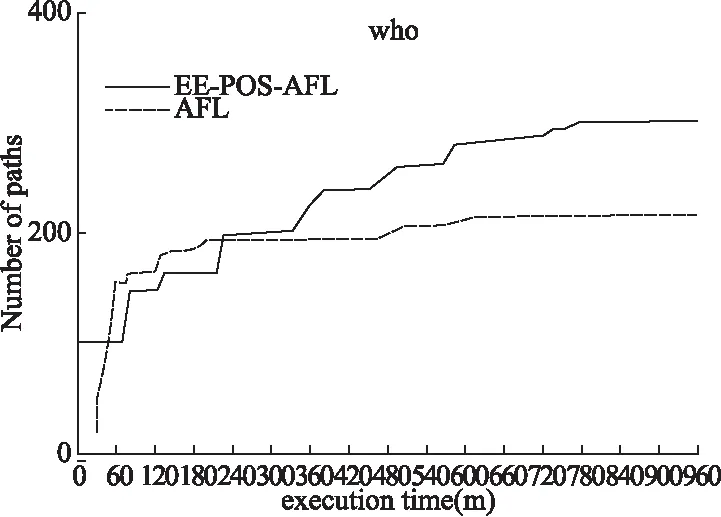
图8 Who 路径发现数量

图7和图8中的变化曲线具有相同的变化规律，因此以图8为例对图像进行分析.在对Who的测试中，前240分钟AFL发现新路径的效率要高于EE-POS-AFL，240分钟到测试结束这段时间EE-POS-AFL发现新路径的效率要高于AFL.这是因为在变异调度优化模型中，变异算子初始状态为人为赋值误差较大，此时AFL的效率高于EE-POS-AFL.随着模型不断地探索，变异算子的状态趋近于最优，此时EE-POS-AFL的效率超过AFL.

对比实验表明本文设计的变异算子调度优化模型相比传统的随机调度模型，路径发现效率提高了63%，Crash发现效率提高了153%，证明了变异算子调度优化模型的有效性.