融合多种拓扑信息的生物网络比对算法
2021-02-28刘晓,陈璟,2
刘 晓,陈 璟,2
1(江南大学 人工智能与计算机学院,江苏 无锡 214122) 2(江南大学 江苏省模式识别与计算智能工程实验室,江苏 无锡 214122)
1 引 言
随着计算机技术的迅猛发展,对复杂网络的研究越来越受到人们的重视[1].其中对生物网络的研究,可以揭示不同物种间的进化关系.生物网络比对是分析不同生物间进化关系的重要手段,它可以帮助理解物种间的进化关系,有助于发现保守功能组件和功能预测[2].
根据网络比对范围分,有局部比对和全局比对,局部比对的目标是在参与比对的网络中找到高度保守的连通子图,通常比对上的区域会比较小.全局比对力图寻找一种映射关系,使得网络中尽可能多的结点被比对上,同时使比对的总体相似性最大.全局比对通常会产生一个较大的比对子图,但比对质量次优.从参与比对的网络个数来分,有成对比对和多比对.成对比对是指对两个网络进行比对,多比对则是指对两个及两个以上的网络进行比对.根据结点间的映射关系,网络比对又可分为一对一比对,一对多比对及多对多比对,一对一是指小网络中的一个结点只能和大网络中的唯一一个结点进行比对,一对多指小网络中的一个结点可以和大网络中的多个结点进行比对,多对多是指小网络中的一个结点可以和大网络中的多个结点进行比对,同时大网络中的一个结点也可以和小网络中的多个结点进行比对.本文算法为全局的,成对的,一对一网络比对算法.
IsoRank[3]是成对全局生物网络领域出现最早的算法,它主要使用了类似于谷歌的页面排序算法进行结点间的相似性计算.PrimAlign[4]在IsoRank[3]所使用的类似页面排序算法的基础上加入了半马尔可夫链进行目标函数计算.度标签相似性的提出给了学者们研究网络拓扑结构的一种新思路.GRAAL家族的系列算法主要使用了度标签相似性来计算结点间的相似性得分,其中GRAAL[5]采用了贪心算法作为搜索算法,HGRAAL[6]使用了匈牙利算法作为搜索算法,MI-GRAAL[7]则使用了节点相似性和网络拓扑结构相似性度量的组合来作为得分函数从而产生比对结果.GoT-WAVE[8]算法借鉴了度标签相似性的思想,提出了使用标签轨道转移的方法进行网络比对.邻域相似性是结点拓扑相似性的一种重要度量方法.SPINAL[9]算法通过借助结点的一级邻居信息来进行结点间的相似性函数计算.CLMNA[10]则提出了一种多邻域的学习方法来发掘结点间的相似性.HubAlign[11]提出了结点的importance概念,认为在网络中重要程度相似的结点更容易被比对上.此外近些年,模块化的思想也被引入到了模块比对中来,其中IBNAL[12]将每个团看作一个模块进行比对,同时为了提高效率,引入了基于团的索引的概念.ModuleAlign[13]则根据模块化结果计算结点间的相似性得分,接着使用动态匈牙利算法进行搜索从而获得比对结果,PINALOG[14]则使用模块化结果来寻找种子对,并使用种子扩展方法进行搜索,AligNet[15]算法则使用了类似分治的策略分别对两个网络中的模块进行子比对,然后再合并子比对结果得到最后的比对.AligNet可以产生高生物功能质量的比对,但由于其对网络结点拓扑信息挖掘不够充分,导致其拓扑质量的提高受限,本文提出了一种新的算法ECAlign,在保证AligNet生物功能质量不降低的前提下,同时将其拓扑质量提高了13%左右,ECAlign主要贡献如下:
1)首次提出了相关值的概念,可以捕捉PPI网络的结构信息,及衡量结点间的相似性.
2)为了更充分地挖掘不同网络结点间的相似性信息,提出了一种基于特征向量中心性的拓扑得分计算方法,并将其应用于模块内比对阶段得分函数的构造.
3)考虑到网络的模块化性质,引入了保守边,以便能最大限度的获取不同网络模块间的边保守性.
2 ECAlign方法
2.1 问题定义
两个PPI网络全局比对,即对输入的两个网络G1=(V1,E1),G2=(V2,E2)进行比对,从而找到一种映射关系F,使得公式(1)成立.
(1)
其中F(u)指通过映射关系F与G1网络中的结点u相匹配的G2中的结点,S(u,F(u))为结点对(u,F(u))之间的相似性得分.
比对算法之间的差异主要是得分函数与搜索算法的不同.得分函数用于评价结点之间的相似性,通常由拓扑与序列相似性组成,由于搜索算法的需求不同,得分函数可以有多个;搜索算法则根据得分函数搜索能使得公式(1)达到最大值的比对关系.类似于多目标优化问题,生物网络比对问题是对拓扑与生物功能的优化,其中一个目标的优化往往会导致另一个目标的劣化[16],因此寻求拓扑与生物功能的平衡是生物网络比对算法的努力方向.
2.2 相关值
文献[17]曾指出,网络结点之间的连接会基于一些相似的性质,即结点与结点之间有某种共性才相连.另外,模块划分是针对同一个网络中的结点进行研究的,而在PPI网络构建时曾提到如果两个蛋白质之间存在相互作用,则对应于网络中连接两个蛋白质的一条边.由此可推,网络结点之间的边隐含了蛋白质间的功能相关性信息,即同一网络中结点的相似性信息被编码在PPI网络的拓扑结构中.根据上述推测,定义如下关系:
强相关.若一对结点之间存在直接相互作用关系,那么称该对结点为强相关结点.对于网络G,其强相关结点集表示为Θ.
弱相关.对于结点(u,v)∉Θ,∃w∈V,其中V为结点集合,使得(u,w)∈Θ∧(w,v)∈Θ,则称(u,v)为弱相关结点.另外若存在弱相关结点(ε,f),且满足(u,ε)∈Θ∧(f,v)∈Θ,也可称(u,v)为弱相关结点.对于网络G,其弱相关结点集表示为Φ.{(u,w),(w,v)}称为(u,v)的一条传递路径,一对弱相关结点可以包含多种传递路径,包含最少强相关结点对的传播路径为最小传播路径.
相关.强相关结点与弱相关结点统称为相关结点,用Ψ表示,则Ψ=Θ∪Φ.
不相关.除ψ之外的其他任意结点对统称为不相关结点,用N表示.
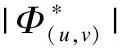
(2)
2.3 基于特征向量中心性的拓扑向量
为了更充分地挖掘不同网络结点间的拓扑相似性信息,本文从结点比对的角度出发,提出了一种用以表征结点拓扑属性的向量元组H=(x,y,z):
1)x(u)表示结点u的度,即u的邻居数;
2)y(u)表示结点u的特征向量中心性,用以衡量结点在网络中的中心性地位.网络中处于中心地位的结点在拓扑结构和功能上都很重要,它们的变异速度往往更慢,因此也更保守,也就是说,它们更有可能被比对上[10];
3)z(u)表示结点u邻居的平均特征向量中心性.待比对结点的邻居结点也会向其提供相似性信息,如果一对结点的邻居结点重要性是相似的,那么这对结点也是相似的.
其中对于图G,其结点特征向量中心性的求解等同于对公式(3)进行特征值及特征向量的求解,其中Q为G的邻接矩阵:
Qx=λx
(3)
计算方式如下:
1)计算邻接矩阵Q的特征分解;
2)选择x中有最大特征值的特征向量m;
3)第i个节点的特征向量中心性等于特征向量m中的第i元素.
本文通过计算不同网络节点间H的欧式距离来衡量两个结点的拓扑相似性,距离越小,相似性越高.对于网络G1=(V1,E1),G2=(V2,E2),结点s∈V1,t∈V2的拓扑相似得分T(s,t)具体计算方式如公式(4)所示:
(4)
2.4 保守边
模块是指同一网络中具有相似功能的蛋白质结点集合.参与比对的两个模块中结点较小者称为源模块,另一个则称为目标模块.源模块与目标模块分别来自不同的网络.如果源模块的两个结点存在一条边,且经这两个结点映射到目标模块后,对应被映射的两个结点之间也存在一条边,则称源模块中的这条边为保守边.如图1所示,模块A中的5个节点分别比对到模块B中的6个节点,虚线表示节点间的映射关系,图中加粗的边即为保守边.例如模块A的结点a与b之间存在一条边,结点a和b分别比对到模块B中结点1和2,而结点1与2之间也存在一条边,则ab这条边就被认为是保守的,则图1中存在ab、bd、cd这3条保守边.
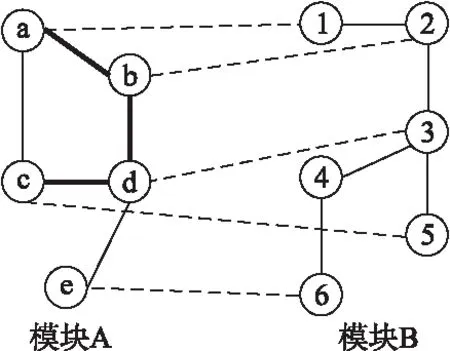
图1 保守边
对于模块M1=(V1′,E1′),M2=(V2′,E2′),边保守得分为公式(5):

(5)
其中M12为两个模块的结点比对映射关系集合,N(vi)指结点vi的邻居集合,A为已经比对上的结点集合.
2.5 算法描述
对于网络G1=(V1,E1),G2=(V2,E2),使用ECAlign算法对其进行比对的基本步骤如下:
Step 1.根据相关值矩阵,分别对G1,G2进行模块划分,得到模块集合CG1,CG2.
Step 2.计算模块中结点的拓扑度量距离,并结合序列相似性将CG1中的模块分别与CG2中的模块两两进行模块内比对.
Step 3.计算两两模块间的局部边保守得分,并根据模块内比对结果对CG1,CG2进行模块间比对.
Step 4.对模块间比对结果进行处理,得到1-1局部比对结果.
Step 5.去除已比对结点,重复Step 2~Step 4,直到至少有一个模块内的结点全部比对上并且所有模块间的权重均为0时停止,得到网络G1,G2的最终比对结果.
ECAlign的伪代码见算法1,其算法流程图见图2.
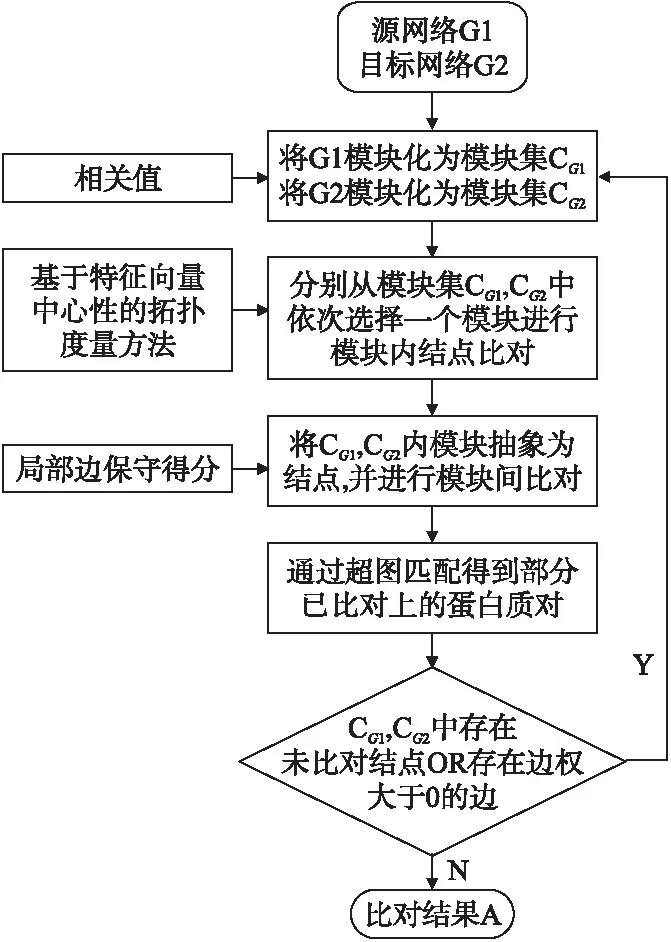
图2 ECAlign算法流程
算法1.ECAlign算法
输入:来自两个物种的网络G1=(V1,E1)和G2=(V2,E2),序列相似性值blast;
输出:比对结果A;
Begin
1.for allu∈V1 do
for allv∈V1 do
根据公式(2)计算结点对(u,v)的相关值;
同理计算G2中结点的相关值;
2.根据相关值分别对G1进行模块化得到M1,对G2进行模块化得到M2;
3.for allm1∈M1 do
for allm2∈M2 do
将m1,m2的中心结点u,v比对上(u,v)在步骤2中产生;
找出u,v的邻居集N(u),N(v);
for allp∈N(u)do
for allq∈N(v)do
根据公式(4)计算(p,q)的拓扑得分T(p,q);
总相似性Fn(p,q)=T(p,q)+blast(p,q);
根据Fn将N(u)N(v)使用匈牙利算法进行比对;
将p,q移除并寻找下一对Fn值最小的已比对结点,将该节点对代替(u,v)并重复本次循环,直到所有结点对扩展完;
4.模块比对;
5.子比对合并;
6.重复步骤1-5,直到所有模块相似性为0或小网络中结点全被比对完;
End
算法1中步骤4,5与ECAlign相同,本文不再详细赘述.
给定网络G1=(V1,E1),G2=(V2,E2),ECAlign总的时间复杂度约为O(k2n).其中k为算法迭代的次数,n为两个网络中结点的最大值.
3 实验及分析
3.1 实验数据集及评价指标
为测试ECAlign的比对效果,本文选取了被广泛使用的IsoBase[18]数据集的最新版本,SPINAL[8],AligNet[15]等算法均使用该数据集进行实验评估.本文将IsoBase中的M.musculus(MUS),C.elegans(CEL),D.melanogaster(DME),S.cerevisiae(SCE)4个物种分别进行两两组合,共得到6个物种对,用以实验评估.4个物种所对应的PPI网络结点数目与边数见表1.
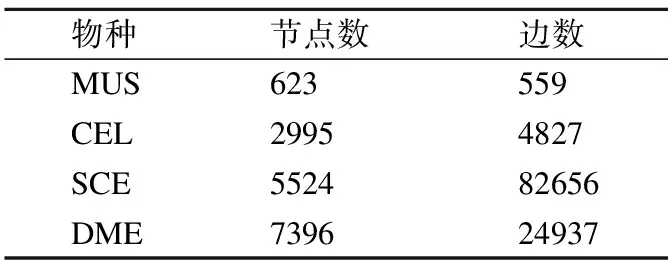
表1 PPI网络信息
目前已经提出了一些比对质量的评估方法,这些方法分为两类,拓扑一致性和生物一致性.拓扑一致性用来评估比对区域的拓扑相似性.生物一致性用来评估蛋白质对的功能相似性,本文使用EC和AFC来分别作为比对结果的拓扑与生物评价指标,具体定义如下:
令G1=(V1,E1),G2=(V2,E2),且|V1|≤|V2|.设u1,v1∈V1,F为获得最终结果的一种映射函数F:G1->G2,F(u1),F(v1)∈V2,则EC(Edge Correctness)为在F映射下保守边的比例.
(6)
功能一致性定义如下:
(7)
(8)
其中GO(u)指结点u所包含的GO术语[19],NFS(Nodes Functional Score)通过计算一对结点对之间共享GO术语的比例来表示其功能相似性.AFC(Average Functional Coherence)则为所有比对结点相似性的平均值.
拓扑质量的评估方式:首先根据获得的比对结果计算结果中所包含的保守边.其次计算网络G1中比对上的结点所包含的边数,保守边与该边数的比值即为比对结果的拓扑质量得分.拓扑质量得分主要评估了算法在边保守方面的能力.
生物质量的评估方式:对于每一对比对上的结点,计算它们所拥有的共享GO术语数,每个GO术语代表蛋白质所拥有的一种生物功能,共享GO术语越多,代表蛋白质越相似.共享GO术语数与两个蛋白质所拥有的GO术语种类数的比值记为两个蛋白质的结点功能得分.所有已比对蛋白质对的结点功能得分均值即为整个比对结果的生物质量得分.生物质量得分主要评估算法获得功能高度相似的蛋白对的能力.
3.2 实验结果与评估
3.2.1 ECAlign与AligNet比较
因ECAlign是在AligNet的基础上提出的,故将其与AligNet进行比较,结果见表2,指标得分最好的采用加粗表示.就拓扑质量EC而言,除在SCE-DME上保持与AligNet相同的拓扑得分外,ECAlign在其他物种对上的得分均高于AligNet;同时ECAlign不但在大部分物种对上获得了与AligNet相同的生物功能质量,且在MUS-DME与CEL-SCE两个物种对上的AFC得分均超过了AligNet.因此ECAlign成功做到在保证AligNet生物功能不降低的前提下,提高了其拓扑比对质量.
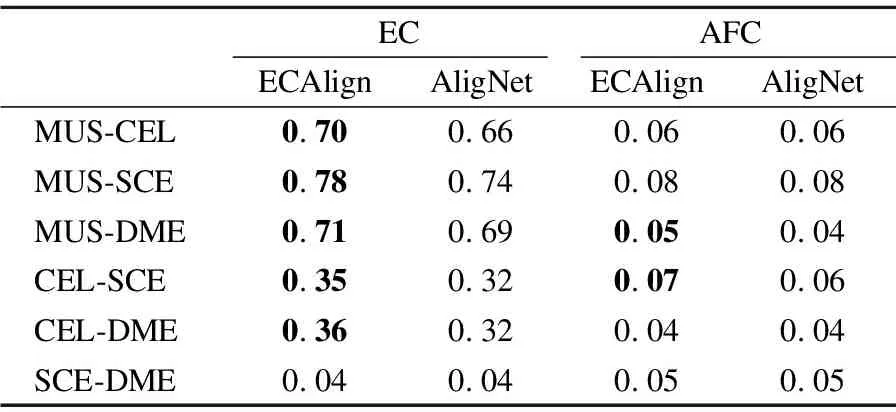
表2 ECAlign与AligNet得分
3.2.2 ECAlign与其他算法
本文将ECAlign与其它主流网络比对算法AligNet,SPINAL,ModuleAlign进行比较,其中ECAlign,AligNet,ModuleAlign均使用了模块化思想进行网络比对,而SPINAL是一种可以获得高生物质量的比对算法.图3、图4给出了4种算法的EC,AFC得分.
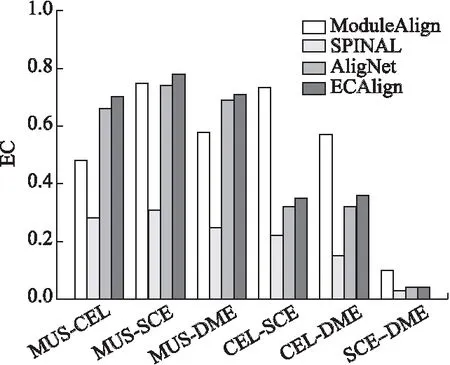
图3 比对算法的EC得分
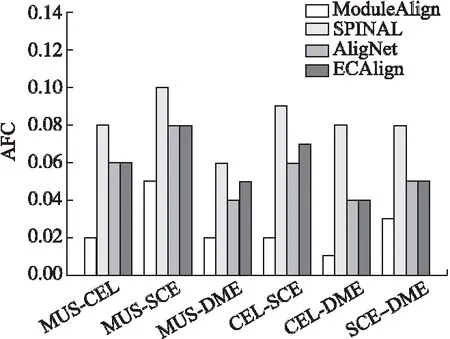
图4 比对算法的AFC得分
由图3可知,在物种对MUS-CEL,MUS-SCE,MUS-DME上,ECAlign的EC得分最高,尤其在MUS-SCE上,AligNet的比对质量较ModuleAlign低,但通过改进得到的ECALign获得了比ModuleAlign更高质量的比对;ECAlign在其他物种对上的表现仅次于ModuleAlign,倾向于对结点数目差距较大的网络产生好的比对结果,但ModuleAlign在不同物种对上表现的稳定性相比其他算法较差,比对质量好坏不一.
由图4可知,ECAlign的AFC得分仅次于SPINAL,但实际上与SPINAL差距很小.综合来看ECAlign,AligNet,与SPINAL的AFC得分在大部分物种对上的差距都很小,基本保持在0.02左右,因此3种算法都可以产生高生物功能质量的比对结果,而ModuleAlign在所有物种对上的表现都是最差的.
3.2.3 不同算法的综合表现
为综合评估算法在拓扑与生物功能上的表现,本文使用Ulign[20]中的trade-off作为评估度量,其值为算法的拓扑得分与生物功能得分的几何平均值,由于EC与AFC值范围存在差异,本文分别将每种方法在不同物种对上的EC、AFC平均排名代替trade-off中的拓扑与生物得分,最后得到的trade-off为算法的综合排名,见表3.可知,ModuleAlign综合表现最差,主要因为其在生物功能方面表现最差且拓扑表现不稳定.AligNet无论在拓扑还是生物质量方面都没有并特别突出的表现,当综合比较时,其劣势得到了放大,因此排名较差.SPINAL表现呈现两极化,拓扑表现最差但生物功能质量最好,生物质量对拓扑质量的弥补使其综合表现次优.ECAlign综合排名最高,也即其综合表现最好,得益于其高拓扑质量与生物质量的共同作用.

表3 比对算法的trade-off排名
4 结 论
生物网络比对有助于帮助发现保守的功能成分和实现功能预测,本文提出的生物网络比对算法ECAlign,通过在各阶段得分函数中融入不同的拓扑信息,从而获得了高拓扑质量的比对结果,同时其生物功能质量也有所提高,其综合表现也是最佳的.
当源网络与目标网络结点数相差太大时,会导致很多目标网络结点无法被比对,从而无法获得这些结点的功能相关信息,下一步的工作重点是寻找一种能最大范围覆盖目标网络的比对算法,从而使其蛋白质功能尽可能被挖掘.
