超大型水中沉井下沉阻力研究

李嘉成 ，陈培帅 ，李德杰

（1.中交第二航务工程局有限公司，湖北 武汉 430040；2.长大桥梁建设施工技术交通行业重点实验室，湖北 武汉 430040；3.交通运输行业交通基础设施智能制造技术研发中心，湖北 武汉 430040；4.中交公路长大桥建设国家工程研究中心有限公司，北京 100120）

0 引言

沉井具有水平和竖向承载力大、防撞性能好、抗震性能强等诸多优点[1-2]，被广泛应用在港口、桥梁、矿山及水利水电工程中。随着我国桥梁建设向宽阔水域、外海发展，一座座跨江跨海特大型桥梁应运而生，超大型沉井基础逐渐成为桥墩基础的主要形式之一[3-7]。然而，特大型沉井基础面临着更大的水深以及更复杂的地质条件，下沉期间存在难沉、倾斜、翻砂突沉等一系列问题。为实现沉井可控下沉，准确确定下沉阻力至关重要。但是，对于土层的侧摩阻力和地基承载力的取值，地勘资料一般仅给出其标准值，而标准值与极限值之间无换算关系，因此确定土层侧摩阻力和地基承载力极限值往往依赖于经验，缺乏理论支撑。

本文依托常泰长江大桥5 号墩沉井基础，利用有限元极限分析方法和理论公式分别对地基极限承载力、极限侧摩阻力进行计算，同时与CPTU静力触探试验实测值进行了比较分析，以期获取与工程实际更为接近的地基极限承载力和极限侧摩阻力，从而实现沉井精准可控下沉。

1 工程概况

常泰过江通道位于泰州大桥与江阴大桥之间，距离泰州大桥约28.5 km，距离江阴大桥约30.2 km，主航道桥采用双层斜拉桥，主塔为沉井基础[8]。其中，5 号墩沉井基础平面呈圆端形，立面为台阶形，其底面尺寸95.0 m×57.8 m（横桥向×纵桥向），顶面尺寸 77.0 m×39.8 m（横桥向×纵桥向），总高为72.0 m；该沉井为钢壳混凝土结构，井壁厚2.0 m，隔墙厚度为1.4 m。沉井定位坐床后采用海床式静力触探系统（PeneVector-IIIA）在现场进行原位试验，试验计划在9 个孔位进行静探试验，由于设备原因仅完成1 号、2 号、4 号和8 号4 个孔位试验，沉井结构及静力触探孔位见图1。

图1 5 号墩沉井结构及静力触探孔位（mm）Fig.1 No.5 open caisson structure and static penetration hole location(mm)

2 沉井下沉阻力的研究

目前，超大型沉井下沉计算中土层参数取值依赖于地质勘探资料，但是地勘资料中地基承载力和侧摩阻力建议值通常偏于保守，故沉井往往需要较大的下沉系数才能启动下沉。为了精准指导沉井下沉，制定高效合理的取土下沉指令，关键在于获取与工程实际更为接近的端阻力和侧摩阻力。

2.1 计算参数

常泰长江大桥5 号墩沉井下沉深度范围内（标高-75.0 m 以上）主要为砂层，其中有4 层粉质黏土层，根据地勘资料的各土层物理力学参数如表1 所示。

2.2 下沉阻力计算

沉井端阻力的计算可归结为刃脚土体极限承载力的问题[9]。针对刃脚处土体的极限承载力，国内外许多学者进行理论研究，主要分为滑移线法、极限分析法、极限平衡法和有限元分析法[10]。其中，滑移线法和极限分析方法，推导过程复杂不易于工程设计人员掌握；极限平衡法相对简单，许多参数以图表的形式给出，便于在工程中推广使用，但是该方法把刃脚简化为条基，未能考虑刃脚楔形体对地基极限承载力的影响；另外，一些学者利用有限元软件对刃脚处地基承载力进行计算，但是有限元计算中地基破坏没有定量的判断标准。近年来，有限元极限分析方法应运而生，它能通过降低土体强度或者增加荷载直接算得岩土工程的滑动面，进而判断地基、边坡及隧道的稳定性[11]。

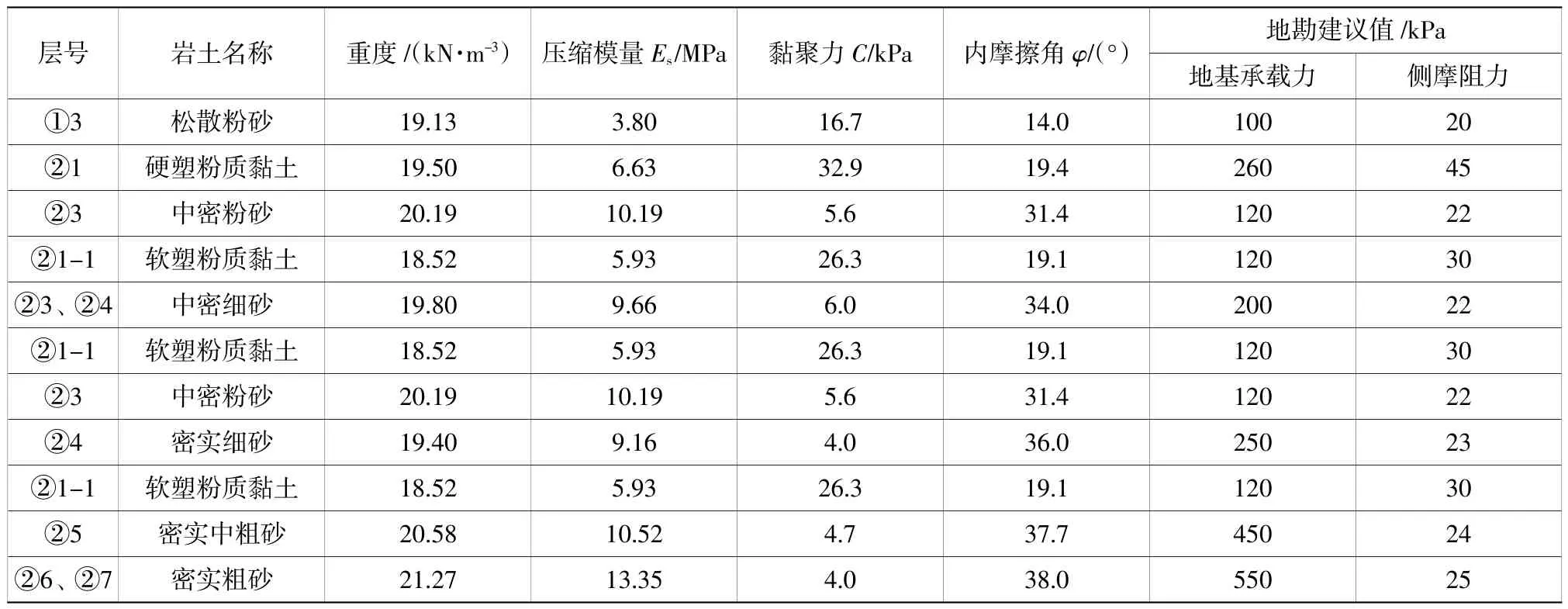
表1 5 号墩沉井土层物理力学指标Table 1 Soil physico-mechanical index of the No.5 open caisson

鉴于此，本文采用有限元极限分析方法计算刃脚处土体的极限承载力。首先，建立二维极限分析有限元计算模型，土体采用M-C 本构模型，其物理力学参数见表1；沉井刃脚弹性模量为30 GPa，泊松比0.25；刃脚采用局部模型，其宽度为B=2 m，高度为2.5B=5 m，刃脚切削角度为45°；土体水平方向向刃脚外每边延伸长度为20 m、深度方向为20 m，其左右两侧约束水平方向位移，土体底部约束水平及竖向位移，沉壁两侧约束水平位移；模型中利用在沉井外侧施加均布荷载等效为外侧覆土来考虑覆土深度。模型中通过在刃脚顶部施加荷载，该荷载从初始值逐渐增加到土体达到极限破坏，土体极限破坏时对应的荷载即为极限荷载，计算模型、边界条件及网格划分如图2 所示。

图2 计算模型及网格划分Fig.2 Calculation model and meshing

图3 为刃脚处地基土体破坏时塑性区云图，由图可知刃脚倾斜面侧土体出现整体滑移即发生整体剪切破坏，其剪切破坏面是从刃脚踏面处开始一直延伸至土体顶部，利用该方法依次计算各土层地基极限承载力。

图3 刃脚切削土体极限破坏Fig.3 The ultimate failure mode of cutting edge in cutting soil

随着沉井下沉深度的增加侧壁摩阻力的占比越来越大，因此侧阻也是下沉阻力的重要组成部分。迈耶霍夫（1976 年）[12]认为土体与打入桩之间极限侧摩阻力由有效应力强度参数控制，由式（1）表示：

式中：σv为桩埋深范围内的平均竖向应力；c 为土体黏聚力；φ为土体内摩擦角；k 为土体的侧压力系数，取k=1-sin φ。沉井下沉过程与打入桩相似，故参考打入桩极限侧摩阻力计算公式计算各土层侧摩阻力。理论计算得到的极限地基承载力和极限侧摩阻力结果见表2 所示。

表2 理论计算与静力触探试验推算结果Table 2 Theoretical calculations and static cone penetration test results

3 静力触探数据分析

双桥静力触探试验可获取锥尖阻力qc、侧壁摩阻力qs，对4 个孔中各土层的锥尖阻力和侧摩阻力求取平均值（见表2），然后根据相关规程中总结的经验公式可对各土层的地基极限承载力和极限侧摩阻力进行推算。

针对极限承载力，可参考TB 10018—2018《铁路工程地质原位测试规程》[13]给出的天然地基极限承载力（Pu）计算公式，各土层极限承载力经验公式见表3 所示。

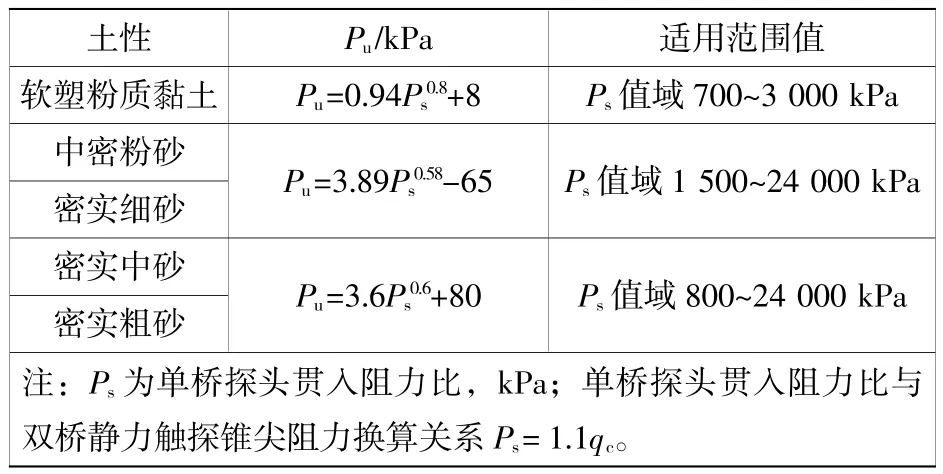
表3 天然地基极限承载力（Pu）算式Table 3 Formula for ultimate bearing capacity(Pu)of natural foundation

对于极限侧摩阻力，双桥静力触探对土层侧摩阻力进行了测试，但是真实极限侧摩阻力的取值并不能直接采用测试的侧阻力结果。其原因是静力触探探头贯入过程中产生超孔隙水压力且超孔隙水压力分布不均，摩擦筒底部的超孔隙水压力大于摩擦筒顶部的超孔隙水压力，从而超孔隙水压力和摩擦筒侧壁土体一起阻止探头贯入，故双桥探头测试的侧摩阻力大于真实侧摩阻力[14-15]。文献[16]针对侧阻真实值与侧阻实测值进行了试验研究，并提出侧阻真实值约为侧阻实测值的37.8%。本文采用该比值对侧阻实测值进行修正。将锥尖阻力qc、侧壁摩阻力qs代入公式，分别计算出各土层的地基极限承载力和极限侧阻力推算值，计算结果如表2 所示。

4 结果对比分析

为了验证结果的合理性，将理论计算结果与静力触探试验推算值进行比较分析。有限元及理论计算值与静力触探值的对比如表2 所示。由表可知，理论计算结果与静力触探试验推算结果两者基本吻合。静力触探试验推算地基极限承载力与计算的地基极限承载力相对偏差均在15%范围内，静力触探试验推算侧阻力与计算侧阻力相对偏差在20%范围内，计算误差满足工程需求，表明了计算结果的合理性。但是，静力触探的地基极限承载力基本大于理论计算值，因为刃脚楔形体有一定的切削角度便于沉井切土下沉，且由极限分析计算结果可知刃脚处土体破坏时仅斜面侧土体发生整体剪切破坏，而条形基础在其左右两侧均发生整体剪切破坏，抗力相对较大，故静力触探试验参数套用条形基础的极限承载力经验公式的计算值偏大。

5 结语

1）有限元极限分析方法计算地基极限承载力和理论计算的极限侧摩阻力与静力触探试验推算值比较接近，初步验证了地基极限承载力和极限侧摩阻力计算方法的合理性，为沉井下沉阻力计算提供思路。

2）极限破坏时，沉井刃脚仅在斜面侧产生贯通滑动面，而条形基础在其左右两侧均产生贯通滑动面，故静力触探套用条形基础的极限承载力经验公式计算值较有限元极限分析方法的计算值偏大。

3） 本文为沉井下沉阻力计算提供了一定依据，但是实际施工过程中地质情况复杂，需在沉井下沉过程中，加强对土层参数的反演计算，同时根据反演结果及时调整开挖下沉工艺。