潜艇气动不平衡式鱼雷发射内弹道两种仿真计算方法比较

徐先勇 马培锋 杨小库

1.海军士官学校兵器系 安徽 蚌埠 233012；

2.中国人民解放军92767部队技术处 山东 青岛 266100；

3.中国人民解放军92246部队工程师 浙江 舟山 316000

引言

从发射阀开始运动起，到鱼雷圆柱段完全离开发射管前气密环时止，这一过程称为发射鱼雷的内弹道。潜艇气动发射装置内弹道设计，实际上就是在上述条件下，研究不同发射深度时，选择不同的发射阀出流面积，来实现鱼雷管内的运动规律[1]。

本文采用两种不同的方法来计算鱼雷内弹道。第一种方法是把气动不平衡式发射装置看成是发射气瓶环节、发射管环节以及无泡水柜环节串联而成的系统。对每个环节直接使用开口系统的热力学第一定律建立数学模型，然后组合起来就构成了整个发射装置的内弹道数学模型。第二种方法是以气动不平衡式发射装置的发射管内部流场为研究对象，基于有限差分原理，利用Fluent软件的动网格技术对流场数值计算方法对武器水下发射内弹道进行仿真。

1 内弹道热力学数学模型

1.1 发射管内的热力过程

鱼类发射装置如图1。忽略通过管壁的热交换，对该对象使用热力学第一定律、其热力过程描述如下：“留在发射管内的气体的内能等于：发射管内原始气体的内能加上通过发射阀注入发射管的热焓之累积值，减去通过泄放阀流出发射管的热焓之累积值，减去气体推进鱼雷所作的功，再减去从鱼雷和管壁间隙中推出海水所作的功。”

图1 气动发射装置示意图

1.2 发射装置内弹道数学模型

文献[2-3]给出了详细的内弹道微分方程组，加上计算发射阀和泄放阀开启面积以及其他参数的代数公式，共同构成气动不平衡式鱼雷发射装置内弹道数学模型[2-3]。

1.3 仿真结果与分析

给定变量初值和参数值以后，采用稳定性好，程序简单的四阶Runge-Kutta方法求解。

在某陆上试验站进行了大量的实验，取两种发射深度对实验数据的拟合曲线如图2-3所示。

图2 发射深度100发射管膛压、鱼雷运动加速度、鱼雷出管速度与时间关系

图3 发射深度100发射管膛压、鱼雷运动加速度、鱼雷出管速度与行程关系

从试验和仿真结果对比可以看出：

（1）仿真结果中发射管膛压和出管速度比试验结果偏大，主要原因是密封垫片厚度的选取，垫片厚度对膛压影响显著。

（2）发射深度对发射管膛压及鱼雷出管速度的影响不是特别明显。膛压峰值一般在2.8s左右出现。而鱼雷出管速度一般在鱼雷管7m以后出现，这与发射管气密环的位置是吻合的。

2 发射器内弹道流场数学模型

2.1 气动不平衡式鱼雷发射装置内弹道流场的特点

气动不平衡式鱼雷发射装置内弹道流体的运动非常复杂，归纳起来有如下特点：

（1）为了能真实反应鱼雷发射过程中各种流场参数的变化情况，应建立流场的三维数学模型，虽然这种三维的数学模型很接近实际物理模型，但其数值计算却非常困难，有时甚至不可能实现。为了计算方便在流场仿真的过程中，发射管及鱼雷假定为轴对称模型，模型简化为二元流动模型。

（2）管内气体的流动复杂，是一种有粘流和非定常流。

（3）发射过程时间短，含有湍流形式，且且发射过程时间极短。

2.2 发射管内弹道模型

如图5，鱼雷受到管壁摩擦力fT、迎面阻力、重力G、尾部气体推力PC以及外部海水静压力PH等的作用，其运动方程为：

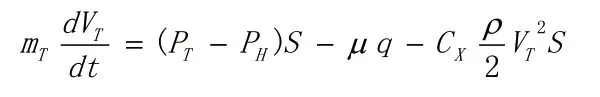
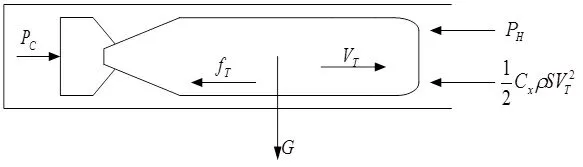
图4 发射过程中鱼雷在发射管内中的受力情况

2.3 模型的建立

根据特定深度鱼雷其运动速度只与它尾部气体压力有关，压力与尾部形状无关，把发射管形状视为轴对称体，模型简化为二维轴对称模型。对几何模型进行网格划分，即可得到网格模型。对发射管与鱼雷之间密封环处进行细化处理，在保证精度的前提下提高数值计算速度。

2.4 数值仿真计算

综合采用网格重建法和运动层法实现流场仿真的动网格处理。在Fluent中设定边界条件及流体属性，设置动网格参数。编写鱼雷运动函数并编译，初始化模型并开始计算，计算收敛后，对计算结果和模型进行报存。

2.5 仿真计算结果分析

Fluent对计算结果进行分析处理，对流场的空间分布用可视化的方法显示，图6为鱼雷出管前发射管内部压力分布图。

图5 武器运动过程中发射管内部压力分布图

根据对鱼雷受力模型计算，鱼雷膛压和出管速度的仿真结果如图6、图7所示。

从仿真结果可以看出：

（1）鱼雷在发射管内运动的整个过程中，发射管内的压强在不同时刻其空间分布不均衡。

（2）在发射开始阶段，鱼雷与发射管环型间隙的节流导致流体的压强从入口开始逐渐减小。

（3）随着鱼雷运动与发射管环型间隙逐渐增大，鱼雷尾部的压强始终小于入口压强，发射管后部的压强与单向阀入口处压强逐渐趋于相同[4]。

3 两种内弹道模型比较分析

从仿真结果可以看出，两种内弹道数学模型仿真结果中鱼雷管内膛压及出管速度变化趋势基本相同，说明建立的模型是正确的。热力学内弹道数学模型优点在于逻辑性条理性好，通用且便于领会和仿真计算，但它忽略了压强在发射管内的空间分布特性，必然影响内弹道计算的准确性。流场内弹道数学模型虽然能更为精确地描述武器水下发射的管内过程，但计算的数据量处理特别巨大，利用一般的计算设备来计算，其速度极其缓慢。

图6 膛压仿真曲线

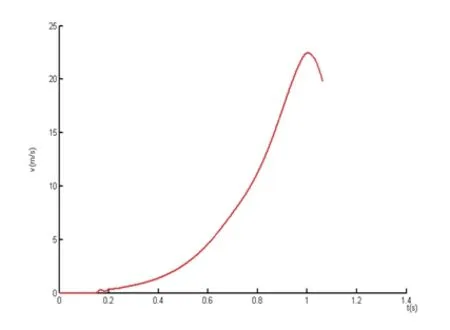
图7 速度仿真曲线