基于共振稀疏分解和松鼠优化算法的滚动轴承故障诊断

夏 俊， 贾民平

(东南大学 机械工程学院，南京 211189)

滚动轴承广泛应用于机械传动系统中，但是滚动轴承的抗冲击能力较薄弱，容易发生损伤失效。在恶劣工况条件下，滚动轴承发生故障时，测得的振动信号往往呈现出高噪声和非高斯非平稳特性。因此，从滚动轴承的非平稳振动信号中提取出准确的故障信息具有重要的研究意义。

现有滚动轴承故障诊断方法主要是基于小波变换、经验模态分解和局部均值分解等时频分析方法[1]。信号共振稀疏分解是Selesnick[2]提出的一种非线性信号分解方法。该方法选择合适的高低品质因子生成小波基函数库，通过形态分量分析对信号进行非线性分离。将信号稀疏表示为持续振荡成分(高共振分量)和瞬态冲击成分(低共振分量)。与传统信号分解方法不同，共振稀疏分解的依据是各组分的波形特性。从本质上看，稀疏共振分解(resonance-based sparse signal decomposition，RSSD)是具有两组特殊小波基函数库的小波分解，突破了传统滤波器基于频带划分的局限性，更适合用于非线性非平稳的机械故障振动信号特征提取，所以相关研究持续增加。

陈向民等[3]首次在滚动轴承故障诊断中使用RSSD方法，对所得低共振分量进行包络谱分析，提取出轴承内外圈故障特征。Wang等[4]针对压缩样本，结合共振稀疏分解和压缩感知理论，有效提取出滚动轴承故障特征。RSSD在滚动轴承故障诊断方面具有优异的表现，但是该方法无法自适应地给出最佳分解参数，从而限制了RSSD的可靠性。主观选取的稀疏分解参数，可能无法发现足够的故障信息甚至产生误判[5]。针对该问题，有研究引入遗传算法和峭度指标来搜索最优的权重系数和品质因子[6-7]。

智能群体优化算法具有良好的搜索性能，能够避免RSSD的无效分解[8]。然而遗传算法本身对于空间最优解的逼近能力较弱，每次迭代的小波分解计算量较大，导致求解效率低。并且品质因子和权重系数两者均直接影响耗散函数的表达形式，利用智能群体优化算法单独优化品质因子或权重系数不能完全发挥其全局寻优性能。

针对以上两个问题，本文将品质因子和权重系数作为松鼠搜索算法(squirrel search algorithm，SSA)的优化对象，提出一种基于多参数优化的共振稀疏分解方法。该方法利用基于SSA优化的RSSD方法进行特征提取，从而获得信号的故障特征频率，并通过仿真信号与实际轴承滚动体早期故障信号实验对方法的有效性进行了验证。

1 基于多参数优化的RSSD方法

1.1 RSSD方法理论

RSSD是将信号的共振属性作为分解的依据，再通过形态分量分析分离出高低共振分量，表示为

y=S1W1+S2W2+n

(1)

该方法通过图1所示双通道分解滤波器组实现信号分解，Hh(ω)和Hl(ω)分别为高通和低通滤波器，其中低通尺度因子(low pass scaling，LPS)α和高通尺度因子(high pass scaling，HPS)β由式(2)得出

图1 双通道分解滤波器组Fig.1 Block diagram of two-channel decomposition filter banks

(2)

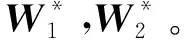
λ1‖W1‖1+λ2‖W2‖1

(3)

1.2 基于松鼠算法的多参数优化方法

冗余因子增大，会使小波频率响应的重叠度增加，导致覆盖相同范围的频率所需的分解级数增加。冗余因子和分解级数只决定RSSD的频率范围。在RSSD参数优化中，最大分解级数为

(4)

品质因子和权重系数是RSSD的关键参数，传统RSSD中参数选择依赖先验知识。本文提出一种基于松鼠搜索算法的RSSD多参数优化方法，以峭度作为优化指标，对品质因子和权重系数进行自适应优化。

松鼠算法是2019年发表的一种群体智能优化算法[10]。与目前用于RSSD参数优化中的粒子群和遗传优化算法相比具有较大优势。SSA采取多策略的更新模式，同时引入季节性监测条件，求解精度和收敛速度得到显著提高。图2是基于SSA的最优分解参数RSSD轴承故障诊断方法的流程图，具体过程为：

创新实践重视不够 实验操作时间分配相对偏少。同时，实验内容设计以基本操作和理论验证为主，轻视仪器的应用分析。格式化的实验操作方式，限制了学生独立动手解决问题的空间，导致学生独立思考时间少，实践动手能力弱[3]。没有熟练的实践技能，不能将理论和实践相结合，不能从解决应用中的实际问题出发思考解决问题，当然也无从进行创新实践和应用。

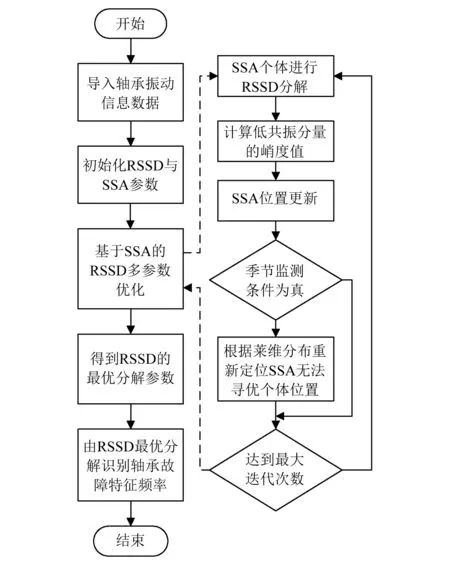
图2 基于SSA优化的RSSD轴承故障诊断流程图Fig.2 Flow chart of bearing fault diagnosis of RSSD based on SSA optimization algorithm

步骤1首先，用品质因子和权重系数作为松鼠位置，并初始化RSSD分解参数。其中低品质因子取0.8～1.3，高品质因子取3～9。权重系数与对应小波函数的能量正相关，初始值取对应子带小波函数2范数的10%～90%。冗余因子取3.5，分解级数按式(4)给出。

步骤2确定松鼠算法的种群规模、迭代次数、滑行距离参数和捕食者存在概率。根据松鼠位置信息做RSSD，对低共振分量进行希尔伯特包络解调分析，以峭度值作为适应度函数。根据峭度值确定山核桃树和橡树位置即全局最优解和局部最优解位置信息。

步骤3对于仍在森林中觅食的松鼠，分别向山核桃和橡树靠拢。在更新位置信息后，计算季节监测值，并与当前迭代次数下最小季节常数对比。若季节监测条件为真，即季节监测值小于最小季节常数，则根据莱维飞行重新定位无法搜索森林的松鼠。

步骤4重复步骤2、步骤3，将满足迭代条件或达到大迭代次数时，结束优化过程。将山核桃树上的松鼠位置信息作为全局最优解，得到自适应的RSSD最优品质因子和权重系数。

2 数字仿真分析

为验证基于松鼠算法优化的RSSD提取故障冲击响应的有效性，对滚动轴承外圈故障的模拟信号进行特征提取并进行抗噪性分析。如式(5)所示，假设滚动轴承的发生外圈故障，周期冲击信号f(t)的特征频率为 250 Hz，转频为60 Hz。单位脉冲响应的载波频率为2 000 Hz，衰减系数为-1 200。轴承外圈故障冲击信号由单位脉冲响应和周期冲击信号表示，图3是故障信号的时域波形。振动信号中还包含60 Hz的谐波分量和服从正态分布的随机白噪声n(t)。

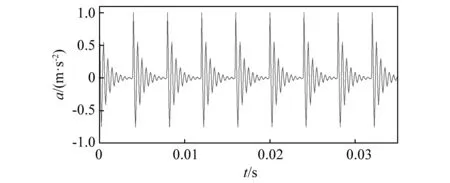
图3 轴承外圈故障冲击信号Fig.3 Shock signal of bearing outer ring fault

(5)

加大噪声，会使得RSSD性能下降。图4是加入不同信噪比的随机噪声，提取2 000 Hz附近的共振区间，进行信号重构，做希尔伯特包络谱分析的频谱图。

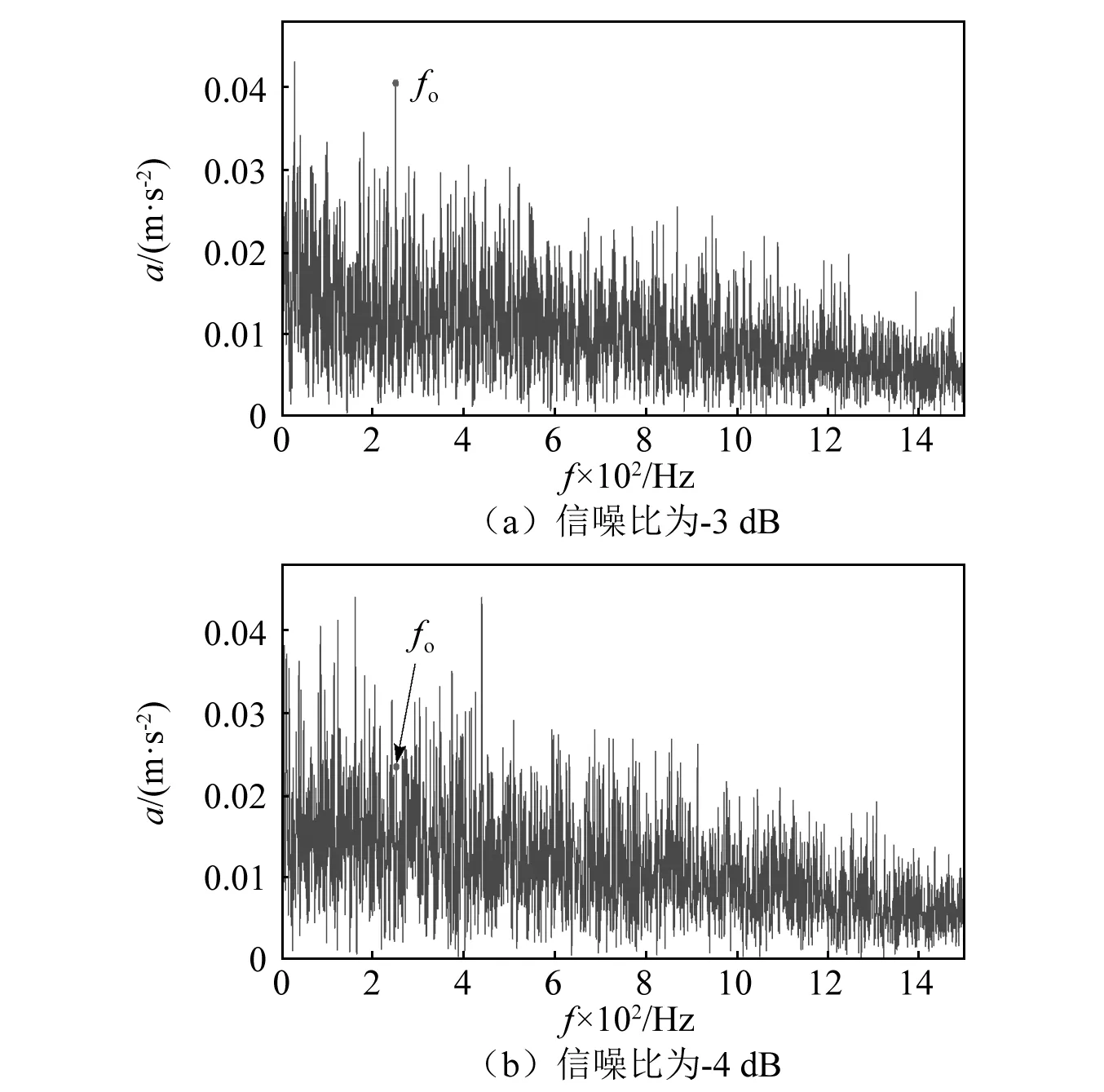
图4 重构信号包络谱图Fig.4 Envelope spectrum of reconstructed signal

如图4所示，在信噪比为-3 dB时能通过希尔伯特包络变换准确识别出250 Hz的外圈故障频率。而当信噪比为-4 dB时，故障特征频率已不能提取。使用本文提出方法进行抗噪性分析，针对信噪比为-5 dB和-6 dB的原始信号直接进行分析，结果如图5所示。

确定SSA搜索区间中位于山核桃的松鼠位置，得到对应RSSD最优分解参数为Q1=4.027,Q2=1.129,λ1=0.748,λ2=0.741。对低共振分量做希尔伯特包络分析，可以从图5中清晰地看到2 000 Hz载波频率附近的250 Hz故障信号。并且RSSD方法无需确认信号的共振频带来进行信号重构。在信噪比低于-6 dB时，本文方法能够准确识别出外圈故障信号，抗噪性能得到显著提升。

图5 低共振分量包络谱图Fig.5 Envelope spectrum of low resonance components

综上所述，对比传统的故障特征频率提取方法，基于SSA的多参数优化RSSD能够在强噪声和干扰信号的情况下，准确提取故障的瞬态冲击成分。

3 滚动轴承故障实验应用

为验证本文方法针对轴承早期故障的诊断效果，采用全寿命强化加速的实验方式获取实验数据。实验装置为ABLT-1A轴承实验台，三个振动加速度传感器分别放置于对应负荷体上。加载方式和传感器布置如图6所示，具体实验条件如表1所示。

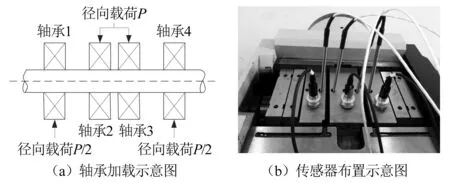
图6 轴承实验平台及加载方式Fig.6 Bearing test platform and loading mode

表1 实验平台参数Tab.1 Parameters of experimental platform

实验中使用均方根值和峭度值监测轴承运行状态，最终由于均方根值达到停机阈值结束实验。在轴承2上发现清晰的滚动体表面剥落故障，如图7所示。取滚动体故障产生阶段数据进行分析。轴承的固有频带在2 000～4 000 Hz，滚动体故障特征频率为102.8 Hz。取固有频带做希尔伯特包络谱分析，结果如图8所示。

图7 滚动体表面剥落缺陷Fig.7 Surface flaking defect of rolling element

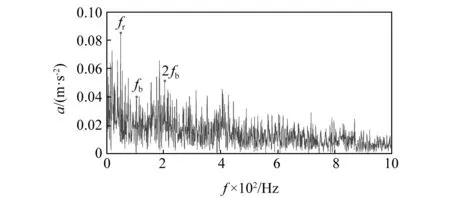
图8 固有频带重构信号包络频谱图Fig.8 Envelope spectrum diagram of natural frequency band reconstructed signal

由于使用全寿命加速实验数据，在滚动体故障成形阶段，传统的取固有频带重构信号，不能有效提取出滚动体故障频率。然后，使用本文提出方法对轴承的滚动体故障进行识别。以峭度值为目标函数，通过SSA寻找最优分解参数。最大峭度值为68.67的松鼠位置对应RSSD分解参数为Q1=7.128,Q2=1.327,λ1=0.746 5,λ2=0.683 1。目标值变化曲线如图9所示，当迭代次数为32时，获得全局最优解。在迭代次数为59和71时，季节判定条件为真，根据莱维分布重新定义未能继续寻优的松鼠位置。这两次重定义，均发现新的橡树位置，即发现新的搜索方向，但是山核桃树位置不变，即全局最优解仍未发生变化。

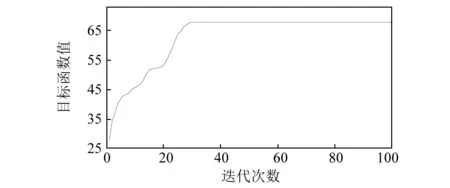
图9 目标函数值变化曲线Fig.9 Variation curve of object function value

使用最优分解参数的RSSD对轴承信号进行分解，得到的低共振分量做希尔伯特包络谱分析，结果如图10所示。

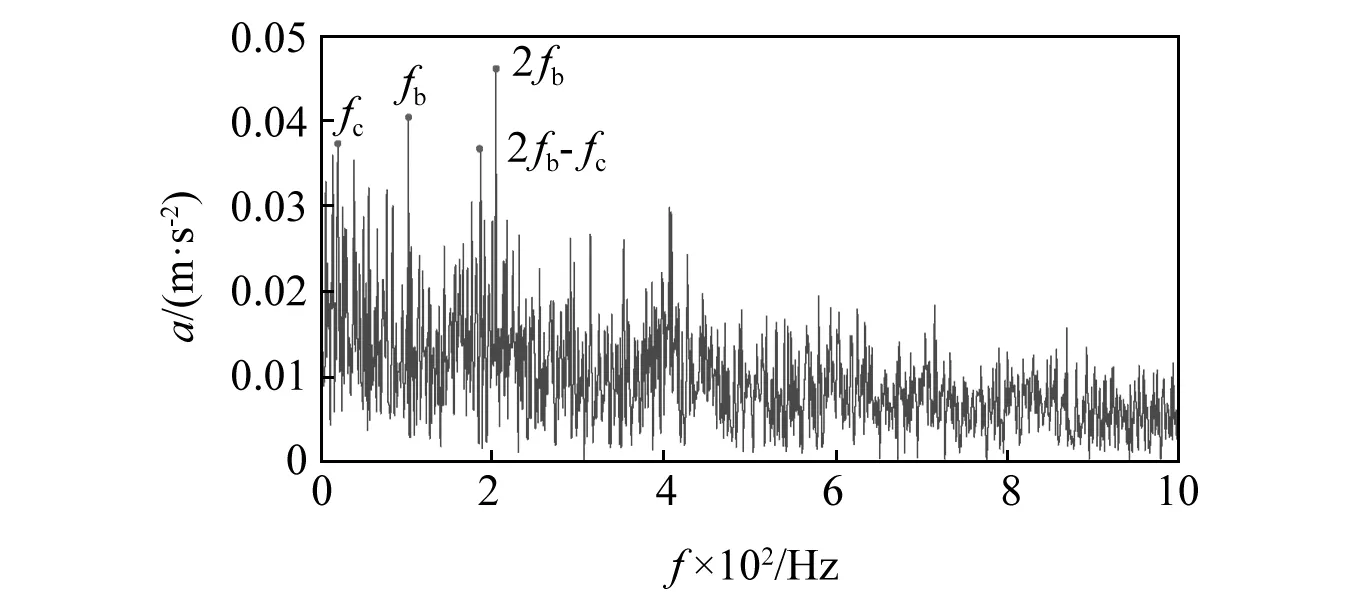
图10 最优RSSD分解参数的低共振分量包络谱图Fig.10 Envelope spectra of low resonance components with optimal RSSD decomposition parameters

从图中看出，在低共振分量的包络谱图中，能够准确识别出滚动轴承滚动体故障，其二倍谐波比较明显。对比传统的轴承故障诊断方法，基于最优分解参数的RSSD诊断能力更佳。

为研究不同分解参数优化方法对于RSSD性能的影响。分别选择Huang等研究中的遗传算法(genetic algorithm，GA)优化RSSD权重系数和Ma等研究中的中粒子群算法(particle swarm optimization，PSO)优化RSSD品质因子与本文基于SSA的多参数优化方法对比，使用特征频率密度系数(characteristic frequency intensity coefficient，CFIC)作为评价指标，定义为

(6)

式中：Aifc为特征频率fc的第i次谐波的幅值;N1为选取的谐波数；Afj为频率fj的幅值；N2为选取频率的范围。特征频率系数越高，说明算法故障特征提取能力越强。选取定滚动体故障频率及其二倍谐波进行分析。表2给出了三种方法的CFIC值和运行时间。

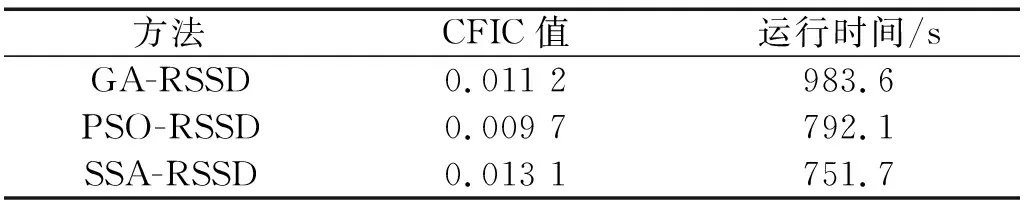
表2 三种方法的CFIC值与运行时间对比Tab.2 The CFIC and operation time comparison of three methods

基于SSA的多参数优化方法具有最大的CFIC值，验证了本文方法对解决RSSD参数自适应选取问题的优越性。RSSD参数自适应优化需要求解多峰问题，现有的优化方法主要对单一品质因子或权重系数进行寻优，导致调Q小波变换的基函数库与耗散函数的参数不能实现最优匹配。同上述方法对比，本文方法提高故障信息的分离精度，同时利用SSA算法计算效率的优越性使得算法的实时性得到提高。

4 结 论

(1)以低共振分量的峭度值作为目标函数值，对调Q小波变换的品质因子和耗散函数的权重系数进行优化，能够有效提高RSSD对故障信息的分量效果。通过仿真实验证明，该方法对比传统故障信息提取方法，具有较好的抗噪性，能够准确提取微弱信号中的故障信息。

(2) 结合SSA算法计算效率与全局寻优能力的优越性，实现对RSSD的多参数优化。通过应用实例表明对比现有单一分解参数优化方法，本文方法可以有效分离轴承的故障信息，实现小波基函数库与耗散函数之间的最优匹配。