流冰对输水隧洞衬砌的撞击影响研究

贡 力， 王 鸿， 杨轶群， 王忠慧， 康春涛

(1. 兰州交通大学 土木工程学院，兰州 730070； 2. 兰州交通大学 调水工程及输水安全研究所，兰州 730070)

我国西北地区冬季严寒，流冰期长且流冰量大，冰凌灾害已成为西北地区输水工程冰期安全运行面临的首要问题[1]。然而位于此地区的输水隧洞由于冬季气候问题，经常受到水介质中流冰的撞击作用，长期的碰撞则会造成隧洞衬砌疲劳累计损伤失效，缩短隧洞使用寿命。而对于在流冰与水工建筑物的撞击方面，实地研究一般较难展开，因此数值模拟以及试验验证的方法在该研究领域内被广泛的应用。

国内外学者对于流冰和水工建筑物以及海上结构碰撞方面进行了研究，Timco等[2]总结了所有与浮冰对结构影响相关的数据，用各种简单的方法对冲击进行了分析,发现冲击力与浮冰在冲击时的动能关系；赵绪新[3]对于空气介质中流冰对于丁坝的撞击破坏进行了数值模拟分析；张宿峰[4]对空气介质下线弹性流冰模型对桥墩产生的撞击压力方面进行了研究；贡力等[5]对在空气介质下线弹性流冰模型与输水隧洞撞击作用方面进行了相应的研究与分析；李明伟等[6]对冰荷载作用下护岸结构的撞击影响进行了数值模拟分析；张健等[7]对水介质中船冰碰撞结构响应影响进行了数值模拟分析；黄焱等[8]对船-冰碰撞载荷时间历程的模型试验进行了研究与分析； Miryaha等[9]提出一种模拟浮冰对海洋结构影响的方法，讨论了典型的浮冰作用模式和海上结构的压力分布。综上所述，国内外的学者对空气介质下流冰与桥墩和海上结构撞击研究较多，但针对水介质作用下流冰与寒旱地区输水隧洞衬砌的撞击作用研究较少。

因此，为了正确模拟碰撞过程中流冰-水-隧洞衬砌三者的相互作用，理清水介质对流冰-隧洞衬砌碰撞结构响应的影响，还原更加真实的碰撞场景，本文采用数值模拟结合试验验证的方法，运用LS-DYNA有限元软件及室内物理模型试验完成水介质中流冰与隧洞撞击的研究与分析，探究不同碰撞工况下流冰对隧洞衬砌撞击的力学性能规律，为西北寒旱地区冰期输水安全提供支持。

1 流冰-隧洞碰撞有限元模型建立

1.1 流固耦合

在流冰与输水隧洞衬砌接触之前的近场逼近过程中，流冰与隧洞衬砌之间的水由于受到挤压而预先产生一个高压力场，这是一个不可忽略的重要因素，该压力场使流冰与隧洞衬砌之间产生一个降低碰撞速度的“水垫效应”，对流冰碰撞起到缓冲作用。因此流冰与结构物的碰撞过程中周围水的影响通过定义流固耦合来解决，流冰与隧洞衬砌采用拉格朗日网格，水介质与空气介质采用欧拉网格，定义流固耦合关系可实现拉格朗日网格与欧拉网格相互作用，相互作用力通过耦合面进行转换与传递。耦合面是一个正体积的封闭面，且至少与一个欧拉单元相交。

1.2 碰撞模型建立

水介质中流冰与隧洞衬砌相互作用是一种比较复杂的非线性动态响应过程，本文在不影响仿真结果的基础上，对碰撞模型进行适当的简化。选取西北寒旱地区“引大入秦”工程盘道岭37#隧洞作为研究对象，利用 ANSYS 软件建立水介质中隧洞和流冰的碰撞模型，并结合非线性有限元软件 LS-DYNA 进行计算分析。隧洞衬砌混凝土材料模型采用美国联邦高速公路管理局( FHWA) 开发的CSCM-CONCRETE模型, 该模型是美国联邦高速公路管理局开发用来分析路边防护栏与汽车撞击性能的。该模型主要考虑了材料的硬化、率相关性以及损伤等，目前在混凝土材料低速冲击方面应用广泛[10]。具体材料参数如表1所示。

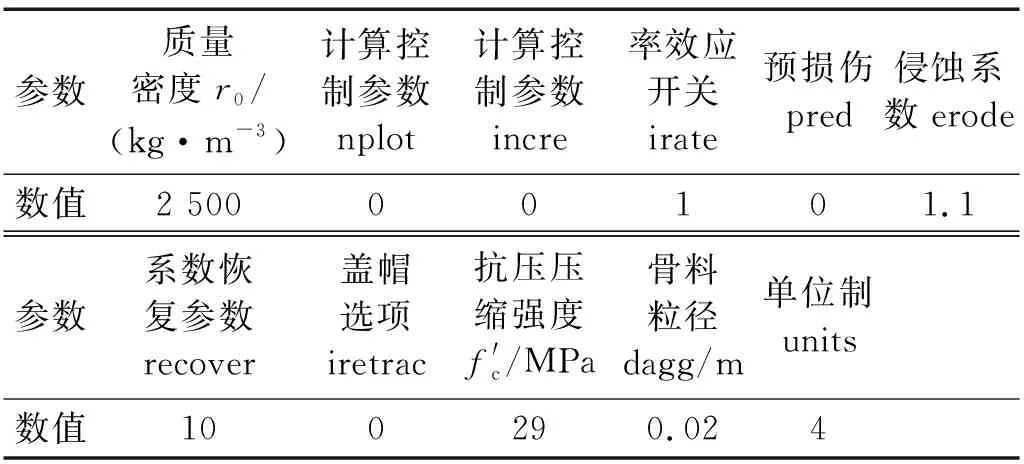
表1 混凝土材料模型参数Tab.1 Concrete material model parameters

对于冰材料而言，由于冰材料具有一定的复杂性，诸多学者在采用LS-DYNA软件进行流冰与水工建筑物方面的碰撞模拟时，选取了LS-DYNA材料库中的不同材料模型，包括各向同性弹性材料、各向同性弹性断裂材料、可压缩性泡沫材料等[11]。本文所采用的流冰材料参考了杨亮等[12]的研究数据，基于流冰碰撞时产生的破碎情况，选取了含有破碎效果的各向同性弹塑性断裂材料作为此次数值模拟的流冰材料模型。流冰材料模型的参数如表2所示。

表2 冰材料模型参数Tab.2 Ice material model parameters

水介质与空气介质材料均选取空白材料，而在状态方程方面有区别是水介质采用的是Gruneisen状态方程描述,空气介质则采用的是线性多项式Polynomial状态方程来描述。具体参数如表3～表5所示。

表3 水介质与空气介质材料模型参数Tab.3 Water and air material model parameters

表4 水介质状态方程参数Tab.4 Water medium state equation parameters

表5 空气介质状态方程参数Tab.5 Air medium state equation parameters

设置材料属性后，对碰撞模型进行建立，建立的水介质中流冰与隧洞衬砌的碰撞模型如图1所示。

图1 水介质中流冰与隧洞衬砌碰撞模型图Fig.1 Model of collision between flow ice and tunnel lining in water medium

图中1为隧洞模型，因为考虑到碰撞作用以及计算时间的问题，选取对称隧洞的一半模型用来求解分析，2为空气域，3为水域模型。根据谭忠华[13]的研究发现，流体计算域大小对计算结果影响很小，考虑到流固耦合计算时间会大幅度增加，为节约计算资源，尽量接近真实碰撞情形，本文选取4.00 m×2.10 m×0.75 m的空气域模型和4.00 m×2.10 m×2.25 m的水域模型，4为处于空气域和水域中的流冰模型,该碰撞模型中流冰模型尺寸为0.5 m×0.5 m×0.2 m，其中流冰厚度为0.2 m。

空气域未选择全域而选取厚度为0.75 m的一层进行计算分析是因为通过观察自然界流冰，漂浮的流冰大部分是浸泡在水介质中的，只有很小一部分处于空气介质中，而本文研究的是中小型的流冰对输水隧洞的碰撞影响，因此空气域对流冰的影响较小，又基于本文采用流固耦合法进行计算分析，如果欧拉网格过多，则会造成流固耦合计算时间的大大增加。因此本文在保证碰撞结果精确性的条件下选取大约4倍流冰厚度的空气域进行整个模型的计算分析。

1.3 边界条件及初始条件

本文将隧洞衬砌底板及边壁进行全约束，漂浮在水面的流冰处于竖向平衡状态，所以在仿真模拟时忽略流冰所受的竖向荷载，只考虑水流拖动流冰运动的水平荷载，其水平荷载主要通过流冰的初速度体现，因此只对水介质中流冰施加撞击方向的初速度[14]。流固耦合模型中还需定义欧拉单元的边界条件和初始状态。水域单元的边界条件是隧洞底板，定义为刚性边界条件，其余部分定义为自由出流边界。空气域单元的边界条件是隧洞边壁，但本文在建立空气域模型时选择建立0.75 m厚的一层空气域而非全域进行模拟，所以空气域与隧洞边壁接触的单元定义为刚性边界条件，其余单元均定义为自由出流边界。

2 碰撞工况选取

引大入秦工程盘道岭37# 隧洞位于中国甘肃省永登县，全长 15.723 km，设计流量32 m3/s，加大流量36 m3/s，设计水深为2.92 m，加大水深为3.37 m，纵坡 1/1 000。该隧洞的结构为反拱底板式断面以及圆拱直墙形结构，隧洞的净高为4.40 m，净宽为4.20 m，半圆形拱顶，其半径为2.10 m[15]。为研究水介质中不同工况下流冰与隧洞衬砌撞击产生的影响以及分析流冰-水-空气-隧洞衬砌四者耦合作用下隧洞衬砌的结构响应问题，本文选取附连水域与空气域的流冰-隧洞衬砌碰撞模型，建立随温度变化的不同流冰压缩强度和流冰厚度与隧洞衬砌的碰撞模型，使不同压缩强度和厚度工况流冰以 3.0 m/s初速度撞击隧洞衬砌。图2为碰撞模型网格划分图，为了精确计算结果，隧洞网格采用分区划分的原则，对隧洞受碰撞区网格进行加密处理[16]。

图2 水介质中流冰与隧洞衬砌碰撞模型网格图Fig.2 Mesh diagram of collision model between flow ice and tunnel lining in water medium

2.1 不同流冰压缩强度工况选取

流冰压缩强度会随着温度产生变化，参照王庆凯等[17]对黄河冰单轴压缩强度的试验与影响分析，温度与流冰压缩强度呈现出对数函数的关系，关系式为

σmax,h=0.767ln(|T|)+0.591,r=0.948

(1)

式中，σmax,h为平行冰面方向加载试样极值压缩强度， MPa；T为温度，℃。

根据天堂水文站实测降水和部分蒸发资料以及邻近气象站资料推得冬季平均气温在-5℃左右，极端最低气温为-28.3 ℃。本文基于以上资料，对-5～-30 ℃温度区间的流冰压缩强度进行选取，通过不同温度来控制流冰压缩强度，在其他参数确定的情况下只改变流冰压缩强度，利用1.2节所建立的碰撞模型，探究水介质中不同压缩强度流冰对隧洞衬砌撞击的作用，根据式(1)选取流冰压缩强度工况如表6所示。

表6 流冰压缩强度工况数据表Tab.6 Data sheet of flow ice compression strength condition

2.2 不同流冰厚度工况选取

通过观察自然界中输水工程流冰大多数属于形状不规则的板类结构，流冰厚度与当地气候条件密切相关，本文综合考虑到大通河冰情和盘道岭隧洞所处地理位置以及参照徐国宾等[18-19]在流冰方面的研究，选取6 cm，10 cm，13 cm，16 cm，18 cm，20 cm厚度流冰，利用1.2节所建立的碰撞模型，探究水介质中不同厚度流冰对隧洞衬砌撞击的影响作用。

3 不同碰撞工况隧洞衬砌动态响应分析

3.1 不同流冰压缩强度

经过水介质中不同压缩强度流冰对隧洞衬砌的撞击模拟分析可以发现，对于小块低速流冰撞击隧洞衬砌时，形成的撞击压力相对较小，且流冰不会呈现出大面积破碎情况，当设置流冰的屈服应力为1.825 MPa时，隧洞衬砌的应力云图及X方向位移云图如图3、图4所示。

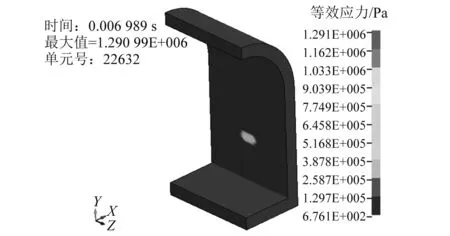
图3 隧洞衬砌最大应力云图Fig.3 Maximum stress cloud image of tunnel lining

图4 隧洞衬砌最大X方向位移云图Fig.4 Maximum X-displacement cloud image of tunnel lining

由图3、图4可知，隧洞衬砌所受的撞击压力在0.006 9 s时达到最大峰值，压力最大峰值为1.29 MPa，且隧洞衬砌撞击区的X方向位移也在该时刻达到最大峰值，位移峰值为2.62×10-5m。在其余压缩强度工况下，撞击压力最大峰值分别为1.42 MPa，1.57 MPa，1.62 MPa，1.67 MPa，1.71 MPa，1.95 MPa，1.91 MPa，1.93 MPa，1.93 MPa，1.93 MPa；隧洞受撞击区X方向位移最大峰值分别为2.73×10-5m，2.79×10-5m，3.00×10-5m，3.08×10-5m，3.05×10-5m，2.98×10-5m，3.05×10-5m，3.12×10-5m，3.14×10-5m，3.10×10-5m；对不同流冰压缩强度工况下隧洞衬砌所受撞击压力以及X方向位移时程曲线进行汇总，如图5、图6所示。

图5 不同压缩强度流冰撞击压力时程曲线Fig.5 Time history curves of ice flow impacting pressure at different compression strengths

图6 不同压缩强度流冰下隧洞X方向位移时程曲线Fig.6 Time-history curve of X-displacement in the tunnel under ice different compression strengths

由图5、图6可知，不同流冰压缩强度工况的压力时程曲线以及隧洞受撞击区X方向位移时程曲线均在同一时刻出现最大峰值且出现多峰值的情况，这是因为水介质中流冰与隧洞衬砌的碰撞过程属于动态响应的过程，第一峰值为流冰在撞向隧洞衬砌的过程中，当其逼近隧洞衬砌时流冰与隧洞衬砌之间的水会形成一个高压力场对隧洞衬砌产生作用，但作用较小，对隧洞衬砌产生的位移不明显。随后的第二个峰值为流冰撞击到隧洞衬砌的作用峰值，此时为整个碰撞过程中的最大峰值，隧洞衬砌受撞击区的位移在此时也达到最大值，由于本文在仿真模拟是采用的混凝土模型为CSCM混凝土模型，该模型在撞击后会记录混凝土的损伤变形。由图6可知，隧洞衬砌混凝土在受到流冰撞击时，会产生较大的变形，这部分变形包括弹性变形以及损伤变形，在撞击过程发生后，隧洞衬砌的位移由最大峰值下降到稳定的损伤变形，由图6可知隧洞衬砌发生的损伤变形在不同流冰压缩强度工况下均稳定在1×10-5m左右。而对于压力时程曲线的后续几个峰值可以看成是由于撞击过程中产生的波浪对隧洞衬砌的影响，这些峰值较小，对隧洞衬砌影响较小，因此本文不做讨论。

3.2 不同流冰厚度

经过水介质中不同厚度流冰对隧洞衬砌的撞击作用模拟分析可以发现，对于厚度较小速度较低的流冰撞击隧洞衬砌，形成的撞击压力和变形相对较小，且流冰不会呈现出大面积破碎情况，当设置流冰的厚度为6 cm时，隧洞衬砌的应力云图及X方向位移云图如图7、图8所示。

图7 隧洞衬砌最大压力云图Fig.7 Maximum stress cloud image of tunnel lining

图8 隧洞衬砌最大X方向位移云图Fig.8 Maximum X-displacement cloud image of tunnel lining

由图7、图8可知，当流冰厚度为5 cm时，达到撞击压力最大峰值的时间为0.008 49 s，撞击压力最大峰值为1.68 MPa，且隧洞衬砌受撞击区的X方向位移也在该时刻达到最大峰值，位移最大峰值为1.62×10-5m。在其余厚度工况下，压力最大峰值分别为2.02 MPa，2.15 MPa，2.20 MPa，2.10 MPa，2.06 MPa；位移最大峰值分别为3.24×10-5m，3.32×10-5m，3.40×10-5m，3.17×10-5m，3.26×10-5m；对不同流冰厚度工况下隧洞衬砌所受压力以及位移时程曲线进行汇总，如图9、图10所示。

由图9、图10可知，不同厚度流冰工况的撞击压力时程曲线以及位移时程曲线也均出现多峰值的情况，原因与3.1节分析原因相同。而与图6不同的是，在图9中撞击压力的第一峰值是同时发生的，这是因为“水垫效应”产生，而第二峰值却出现错位的情况，这是由于不同厚度流冰在水介质中撞击隧洞衬砌的过程中，由于流冰厚度增加，相应的碰撞面积也增加，水介质对流冰的阻力也增大，进而造成流冰与隧洞衬砌接触时间上存在着时间差，所以造成第二峰值出现不同时刻的情况，位移时程曲线峰值也出现不同时刻的情况。由图10可知，隧洞衬砌混凝土在受到流冰撞击时，产生变形情况与3.1节分析一致，但是在撞击过程发生后，不同厚度流冰工况下隧洞衬砌的损伤变形却是均稳定在0～1×10-5m左右。

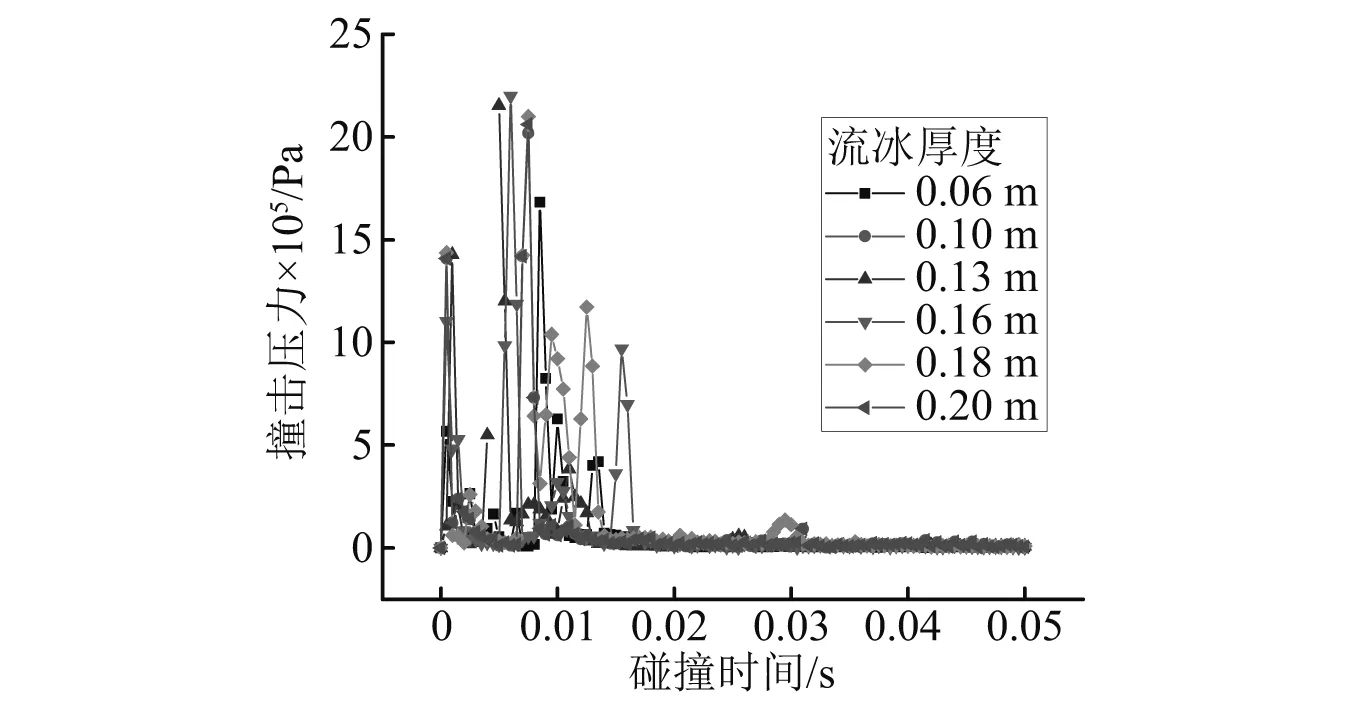
图9 不同厚度流冰撞击压力时程曲线Fig.9 Pressure time-history curves of ice flow with different thickness

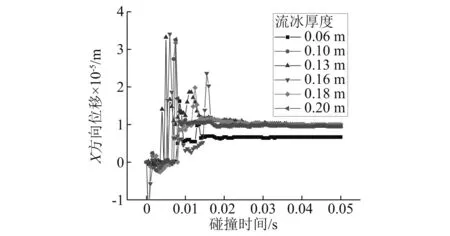
图10 不同厚度流冰下隧洞X方向位移时程曲线Fig.10 Time-history curve of X-displacement in the tunnel under ice flow with different thickness

4 不同碰撞工况下最大峰值结果分析

4.1 不同压缩强度流冰最大峰值分析

对图5、图6中时程曲线的最大峰值进行统计后，绘制不同压缩强度流冰工况下隧洞所受的撞击压力峰值散点图和X方向位移峰值散点图，并进行曲线拟合。如图11、图12所示。

图11 不同流冰压缩强度撞击压力峰值图Fig.11 Peak impact pressure of different ice compression strengths

图12 不同流冰压缩强度下隧洞X方向位移峰值图Fig.12 Peak X-displacement in the tunnel under different ice compression strengths

由图11、图12可知，流冰压缩强度与撞击压力和隧洞撞击区X方向位移均呈现出对数函数的关系，由于水介质、空气介质以及混凝土材料的影响，隧洞撞击区位移的部分点出现偏移的情况，但就整体来说流冰压缩强度与撞击压力和隧洞撞击区X方向位移还是均呈现出对数函数的关系。

(1) 流冰压缩强度与撞击压力的关系式为

y=1.272ln(x)+0.480 3

(2)

式中：y为撞击压力，MPa；x为流冰压缩强度， MPa； 相关系数为R2=0.941 8。

(2) 流冰压缩强度与隧洞衬砌受撞击区的X方向位移关系式为

y=(9×10-6)ln(x)+(2×10-5)

(3)

式中：y为隧洞衬砌碰撞区X方向位移，m；x为流冰压缩强度，MPa； 相关系数为R2=0.896 6。

不同流冰压缩强度对应的隧洞衬砌受撞击区X方向位移峰值拟合曲线相关系数略低，除了空气介质、水介质以及混凝土材料的影响外，还有位移本身的限制条件。因为本文研究小块流冰对于隧洞衬砌的撞击影响，隧洞衬砌撞击区的位移本来就是很微小，所以输出位移会存在一定的误差，导致拟合曲线的相关度略低。

4.2 不同厚度流冰最大峰值分析

对图9、图10中时程曲线的最大峰值进行统计后，绘制不同厚度流冰工况下隧洞所受撞击压力峰值散点图和X方向位移峰值散点图，并进行曲线拟合。如图13、图14所示。

图13 不同厚度流冰撞击压力峰值图Fig.13 Peak pressure of ice impingement with different thickness

图14 不同厚度流冰下隧洞X方向位移峰值图Fig.14 Peak X-displacement in the tunnel under different ice thickness

由图13、图14可知，流冰厚度与撞击压力和隧洞衬砌撞击区位移均呈现出多项式函数的关系，同样由于水介质、空气介质以及混凝土材料的影响，隧洞撞击区位移的部分点出现偏移的情况，但就整体来说流冰厚度与撞击压力和隧洞撞击区位移还是均为多项式函数的关系。由图13、图14可以发现，当流冰厚度在16～20 cm变化的过程中，撞击压力峰值与X方向位移峰值均出现微小的下降趋势，这是由于水介质和流冰厚度的尺寸效应共同导致的。本文所研究的是小块流冰对隧洞衬砌的撞击影响，在增加流冰厚度的过程中，流冰质量增加的相对较少，因此不同厚度流冰的撞击压力和撞击区位移峰值差距会相应的较小，但是随着流冰厚度的增加，水介质对于流冰的阻力相应的增大，对流冰速度的减缓作用增大，且流冰与隧洞衬砌的撞击面积也相应的增大，因此撞击压力和隧洞衬砌X方向位移峰值会出现微小的下降趋势，而不是线性增长的趋势。

(1) 流冰厚度与撞击压力的关系式为

y=-58.739x2+17.865x+0.822 8

(4)

式中：y为撞击压力，MPa；x为流冰厚度，m； 相关系数为R2=0.988 5。

(2) 流冰厚度与隧洞衬砌撞击区的位移关系式为

y=-0.002x2+0.000 6x-(1×10-5)

(5)

式中：y为隧洞衬砌碰撞区位移，m；x为流冰厚度，m； 相关系数为R2=0.913 3。

不同流冰厚度X方向位移峰值拟合曲线相关系数略低原因与4.1节分析原因一致。在此不再分析。

5 水介质中流冰撞击隧洞衬砌的物理模型试验

5.1 试验方案设计

本文通过与数值模拟相对应的室内模型试验对流冰与输水隧洞衬砌的撞击作用进行试验验证[20-21]。室内试验模型与实际模型的几何比尺Cl为 5，材料的密度比尺为1.0，加速度比尺为1.0[22-23]，在常重力场条件下进行试验,试验中水介质采用普通水介质。

试验模型如图9所示，图中字母a，b，c，d，e点所代表的是应变片所在的位置，应变片布置高度为45 cm。

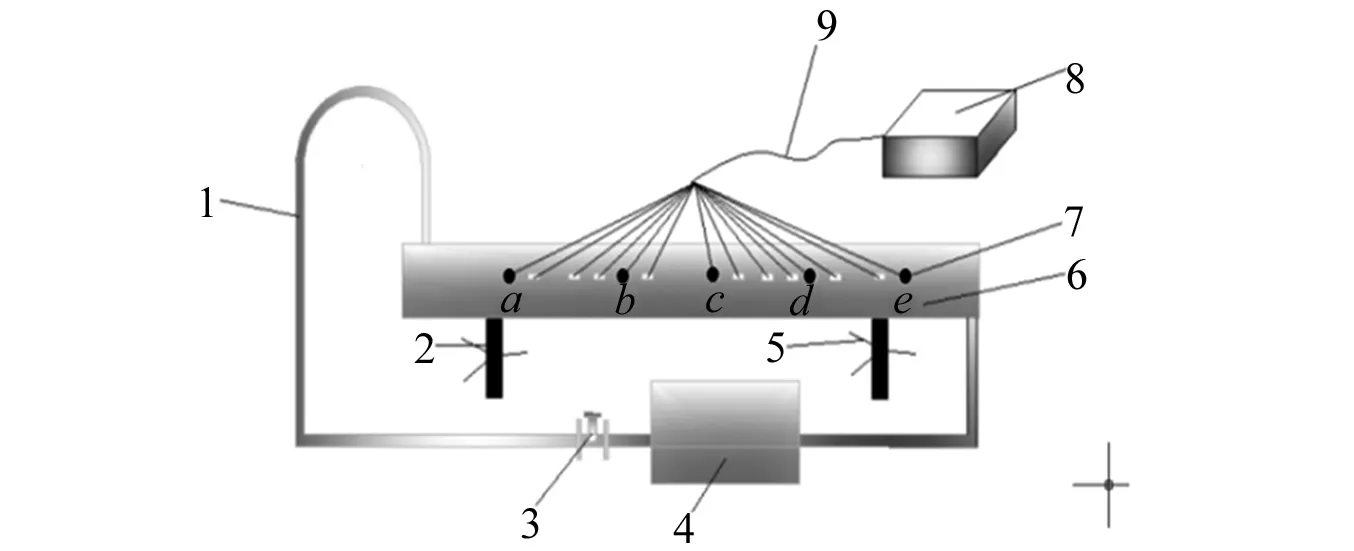
1.循环水管；2.固定支柱；3.水泵；4.水箱；5.旋转螺旋；6.水槽；7.应变片(a, b, c, d, e)；8.测试仪器；9.测试线。图15 试验装置图Fig.15 Test device diagram

5.2 试验内容

(1) 研究流冰压缩强度对隧洞衬砌撞击影响试验。

在水箱中充满水；打开总电源，利用水泵使得水箱中的水流入试验隧洞模型中；将准备好的大小规格为 10 cm×10 cm×4 cm，屈服压缩强度为1.825 MPa的冰块放入隧洞模型中；通过旋转螺旋将水流流速控制在3.0 m/s，流速用流速计测得；利用水位探针控制模型试验水深为45 cm；检查试验模型边壁的10 个有机玻璃应变片是否处于正确位置；关闭瞬态应变测试仪；利用测试线将10个有机玻璃应变片与瞬态应变测试仪进行相应的连接；将瞬态应变测试仪转换为手动操作状态；随着流冰撞击试验模型边壁，观测并记录瞬态应变测试仪上所显示的数据；接着改变流冰压缩强度大小，流冰压缩强度由温度来控制，选择不同温度来对应流冰压缩强度，分别取流冰压缩强度为2.136 MPa，2.357 MPa，2.528 MPa，2.668 MPa，2.786 MPa，2.889 MPa，2.979 MPa，3.059 MPa，3.133 MPa，3.199 MPa，重复上述步骤，最终进行数据整理。观察流冰压缩强度对撞击压力以及隧洞衬砌碰撞区位移的影响情况。

(2) 流冰厚度大小对撞击影响的试验。

改变工况，水深和流速均保持不变，改变流冰厚度，分别取1.2 cm，2.0 cm，2.6 cm，3.2 cm，3.6 cm，4.0 cm厚度流冰；重复上述步骤，观察流冰厚度对撞击压力以及隧洞衬砌碰撞区位移的影响情况。

5.3 流冰压缩强度对隧洞衬砌的撞击影响

根据5.2节中试验内容(1)所得的试验数据，得到不同压缩强度流冰工况下，隧洞衬砌所受的撞击压力值及隧洞衬砌撞击区的位移值，将上述已处理过的试验数据按照模型相似比进行相应的换算，得到如图16所示的软件模拟计算结果与试验观测计算结果对比图。

图16 不同压缩强度流冰试验结果与模拟结果对比图Fig.16 Comparison of ice flow test results and simulation results with different compression strengths

由图16可以发现，在流冰压缩强度改变的条件下，数值模拟结果的最大峰值与试验观测结果所得最大峰值有基本一样的趋势，吻合效果良好。由图16可以看出当流冰压缩强度增大时，流冰对隧洞衬砌的撞击压力随之增大，隧洞衬砌撞击区的最大位移也随之增大，且基本呈现出对数函数分布的关系。

通过误差分析可以发现，在撞击压力方面：数值模拟所得的峰值结果与试验观测所得的峰值结果最大误差为4.12%，最小误差为 0.51%，平均相对误差保持在 1.22%左右；在隧洞衬砌碰撞区最大位移方面：数值模拟所得的峰值结果与试验观测所得的峰值结果最大误差为2.34%，最小误差为 0.1%，平均相对误差保持在 0.88%左右，其计算所得误差均保持在允许范围内[24]。由此可知，本文采用的仿真模型可以准确的模拟水介质中流冰与输水隧洞衬砌的碰撞作用，模拟结果真实可靠。经过分析可知，误差的产生主要是由于试验值波动导致，可能与试验中流冰与模型的二次碰撞以及水介质的作用有关。

5.4 流冰厚度对隧洞衬砌的撞击影响

根据5.2节中试验内容(2)所得的试验数据，得到不同厚度流冰工况下，隧洞衬砌所受的撞击压力值及隧洞衬砌撞击区的位移值，将上述已处理过的试验数据按照模型相似比进行相应的换算，得到如图17所示的软件模拟计算结果与试验观测计算结果对比图。

图17 不同厚度流冰试验结果与模拟结果对比图Fig.17 Comparison of flow ice test results and simulation results with different thickness

由图17可以发现，在流冰厚度改变的条件下，数值模拟结果的最大峰值与试验观测结果所得最大峰值有基本一样的趋势，吻合效果良好。由图17可以看出当流冰厚度增大时，流冰对隧洞衬砌的撞击压力随之增大，隧洞衬砌撞击区的最大位移也随之增大，且基本呈现出多项式函数分布的关系。

通过误差分析可以发现，在撞击压力方面：数值模拟所得的峰值结果与试验观测所得的峰值结果最大误差为1.91%，最小误差为 0.1%，平均相对误差保持在 1.17%左右；在隧洞衬砌碰撞区最大位移方面：数值模拟所得的峰值结果与试验观测所得的峰值结果最大误差为4.85%，最小误差为 0.17%，平均相对误差保持在2.26%左右，其计算所得误差均保持在允许范围内。由此可知，本文采用的仿真模型可以准确的模拟水介质中流冰与输水隧洞衬砌的碰撞作用，模拟结果真实可靠。经过分析可知，误差的产生主要是由于试验值波动导致，可能与试验中流冰与模型的二次碰撞以及水介质的作用有关。

6 结 论

本文与先前研究所不同的是，考虑水介质对于流冰撞击隧洞衬砌的影响，运用有限元分析软件ANSYS/LS-DYNA进行了水介质中不同压缩强度流冰以及不同厚度流冰对隧洞衬砌的碰撞仿真模拟，并开展了相应的室内模型试验，经过研究发现数值模拟结果和试验观测结果具有良好的吻合性，并且根据流冰压缩强度与流冰厚度的变化对输水隧洞衬砌撞击影响得到了以下结论：

(1) 在只改变流冰压缩强度的情况下，隧洞撞击区X方向位移峰值和撞击压力峰值均随着流冰压缩强度的增大而增大，且均呈现出对数函数关系，仿真模拟值与试验观测值误差保持在5%以内。

(2) 在只改变流冰厚度的情况下，隧洞撞击区X方向位移峰值和撞击压力峰值与流冰厚度呈现出近似多项式关系，仿真模拟值与试验观测值误差保持在5%以内，且在本文所模拟的厚度工况下，当厚度在16～20 cm时，流冰撞击压力峰值及碰撞区X方向位移峰值不再随着流冰厚度的增加呈现出增加的趋势，而是由于水介质和流冰厚度尺寸效应的影响作用出现轻微的下降趋势。

(3) 综合分析本文所模拟的不同工况可以发现，水介质对于小型流冰撞击隧洞衬砌过程有较大的影响，不可忽略，且“水垫效应”在碰撞过程中表现的较为明显。

在实际工程中漂浮在水面的流冰其运动是受多因素影响的，如水温与水流流态等；而对于水介质中中小型流冰长期碰撞隧洞衬砌导致其失效作用等问题，还需要做进一步的研究。因此，本文研究内容可以为后续流冰长期碰撞导致隧洞衬砌失效作用研究提供支持，也为西北寒旱地区流冰期输水提供了理论基础和技术保障。