基于增强型形态学滤波的风电机组轴承故障诊断方法

齐咏生， 樊 佶， 李永亭， 高学金， 刘利强

(1. 内蒙古工业大学 电力学院，呼和浩特 010080； 2. 内蒙古自治区机电控制重点实验室，呼和浩特 010051；3. 北京工业大学 信息学院，北京 100124)

风力发电机组传动系统结构复杂，工况恶劣，承受外界载荷多变，易造成机组构件损坏，而滚动轴承是其中最重要也是最易受到损伤的零部件之一。滚动轴承如若发生故障将对整个旋转机械甚至整个风机的运行状态产生重大影响，严重时导致整台机组停机[1]。因此实时监测其工作状态，准确诊断其故障成因对风力发电机组的维护与运行有着重要的现实意义[2]。

轴承振动信号分析是实现风电机组滚动轴承状态检测最有效的工具之一。当轴承表面出现局部损伤时，故障信号包括一系列周期性指数衰减振荡脉冲，这些脉冲还会激发轴承结构共振。然而，实测轴承振动信号多采用加速度传感器直接从箱体上获取，导致其信噪比较低，特别是早期故障信号能量很小，故障特征信息比较微弱，难于提取。此时，若能够将淹没在环境噪声及干扰频率成分下的脉冲信号提取出来，则能较好的检测出故障类型及位置[3]。

形态学滤波(morphological filter, MF)是以数学形态学变换为基础的一种非线性滤波方法[4]，并已被广泛应用于许多重要领域，如图像处理[5]、语音识别[6]、电力信号[7]和机械振动信号分析[8]。其利用特定尺度和形状的结构元素(structure element, SE)与待处理信号的几何特征进行匹配，提取信号边缘轮廓和形状特征，达到消除噪声和保持脉冲特征的目的。近年来，在大型旋转机械滚动轴承故障诊断中，形态学滤波的应用越来越受到重视，并在形态学算子及结构元素的构造选择方面取得一定的成果。Raj等[9]采用膨胀腐蚀梯度算子提取轴承早期故障信号中的脉冲特征，并根据最大峭度选择最优分析尺度；余建波等[10]构造了一种平均组合差值形态算子应用于随机噪声和谐波干扰下的滚动轴承故障特征提取，由Teager能量峭度的大小选择分析尺度；Meng等[11]使用平均闭开-开闭算子去除振动信号中的高频噪声；李奕璠等[12]通过分析比较提出一种基于汉明窗的结构元素，提升了形态学滤波器的效果。Li等[13]提出一种自适应多尺度形态学方法，根据形态闭开-开闭差值运算提取振动信号中故障特征，并用遗传优化算法确定不同尺度下滤波结果的权重。但是，在上述各种形态学滤波的方法研究中，还存在以下一些问题：①在形态学算子及滤波分析尺度的选择上，尚不存在一个明确的指导方法，计算繁杂或欠缺普适性；②由于形态学方法是从图像处理引入到一维机械振动信号的处理中，对其滤波性质和影响分析不够深入；③在实际应用中，仅使用形态学滤波对早期微弱故障进行特征提取和故障诊断能力有限。

此外，在利用形态学提取故障脉冲特征时，脉冲个数并非越多越好，尤其在实际强噪声环境下，滤波时不可避免地提取到一部分伪分量，滤波后带内噪声仍然存在，高频噪声难以完全消除。因此，针对此问题需要对形态学滤波算法进行进一步改进和增强。包络导数能量算子[14-15]是近年来新提出的一种能量算子，可以检测信号的瞬态变化，相较于传统希尔伯特变换和Teager能量算子，该算子基于包络求导运算，计算复杂性低，解调性能更好，非常适合用其进一步提高形态学滤波效果。但在面对噪声和无关频率成分干扰时，其性能会受到一定程度的影响。为此，本文提出使用自相关运算和Shannon熵函数进一步增强包络导数能量算子的抗噪和削弱杂频干扰能力。

鉴于上述问题，本文旨在研究一种增强型的形态学滤波策略，与现有形态学滤波方法相比提高其微弱特征提取和故障诊断的能力。主要的改进之处包括：首先构造一个新的形态学综合顶帽变换(morphological comprehensive filter hat transform, MCFHT)提取微弱故障脉冲，并结合信号自身形状特征自适应选取滤波尺度，用于指导形态学滤波尺度的选择；之后由频响特性剖析其滤波性质，提供实际应用的理论依据和前提条件；最后使用一种改进的包络导数能量算子作为后置增强环节，抑制形态学处理后信号中的带内噪声并进一步突出故障特征。将该方法用于仿真信号和真实风电机组轴承故障信号上，对轴承故障进行检测和诊断，并与现有形态学滤波方法进行比较，结果验证了所提方法的有效性和优越性。

1 一种新的形态学综合顶帽变换及其性质分析

1.1 数学形态学基本理论

基本的数学形态学算子包括膨胀、腐蚀、开运算、闭运算和它们的组合形式。假设原始振动信号f(n)，定义在F=(n=0,1,…,N)，所选结构元素g(m)，定义在G=(m=0,1,…,M-1)，其中N≥M，腐蚀和膨胀的表达式为

(f⊕g)(n)=max[f(n-m)+g(m)]

(1)

(fΘg)(n)=max[f(n+m)-g(m)]

(2)

膨胀和腐蚀运算等价于振动信号在结构元素作用下的最大值和最小值滤波。

开运算和闭运算在膨胀和腐蚀的基础上构造，如式(3)、式(4)

(f∘g)(n)=(fΘg⊕g)(n)

(3)

(f•g)(n)=(f⊕gΘg)(n)

(4)

开运算可以滤除f(n)中的上尖峰部分，保留负脉冲成分；而闭运算可以填补f(n)中低谷部分，保留正脉冲成分。闭开组合平均算子定义为

(5)

AC&O(f(n))算子可以削弱观测信号中的高频噪声，检测双向脉冲分量，获得有助于故障诊断的几何特征和细节，但仍会保留一部分无关波形特征和干扰。

此外，根据开、闭组合形式不同的级联顺序，一种闭开-开闭组合平均算子定义为

(6)

ACO&OC(f(n))算子可以减少窄带脉冲干扰，解决开闭及闭开算子统计偏倚的缺陷，且该算子处理结果非常贴近原振动信号，具有较好的降噪作用，但该算子常常会将故障脉冲同时衰减。

闭开差值形态算子(difference filter，DIF)定义为

fDIF(f(n))=(f•g)(n)-(f∘g)(n∘)=

(f•g-f)(n)+(f-f∘g)(n∘)=

fWTH(f(n))+fBTH(f(n))

(7)

式中：fWTH(f(n))为白顶帽变换(white top-hat, WTH)，用来获取信号正脉冲；fBTH(f(n))为黑顶帽变换(black top-hat, BTH)，用来提取信号负脉冲。

1.2 一种新的形态学综合顶帽变换

形态学在信号处理的基本运算过程是不可逆的，不同算子有着不同的作用和效果。为了更好地发挥各类算子的优势和作用，本文提出了算子的级联组合方式，即利用级联组合综合发挥算子各自的优势和长处。

AC&O(f(n))和ACO&OC(f(n))是两种从不同角度对故障信号进行降噪的工具，我们将其进行级联组合提出一种形态学综合滤波(morphological comprehensive filter, MCF)运算，充分利用其各自的优点，最大限度的整合各单项算子的性能，避免由于仅采用一种算子所带来的缺陷，具体定义为

fMCF(f(n))=μ1AC&O(f(n))+μ2ACO&OC(f(n))

(8)

式中，μ1，μ2为各单项算子的权值系数。

形态学综合算子fMCF(f(n))不仅能削弱噪声反映故障几何特征，还可避免固有的输出偏移问题。在确定各单项算子的权值系数时，分别计算AC&O(f(n))和ACO&OC(f(n))滤波后信号与原信号之间的相关系数r1和r2，从而得到μ1，μ2为

(9)

为了进一步提取降噪后信号中的故障脉冲，本文遵循顶帽变换的基础，利用原信号与MCF的差分运算，整合MCF和Top-Hat，构造了一种基于MCF-Hat(MCFHT)变换的算子

fMCFH(f(n))=f(n)-fMCF(f(n))=f(n)-

[μ1AC&O(f(n))+μ2ACO&OC(f(n))](10)

基于MCFH算子的形态学滤波器在保持原信号降噪的作用上，消除低频波动，并利用顶帽变换进一步加强了对故障脉冲的提取能力。

为了得到更好的滤波效果，使用不同尺度对f(n)进行形态学变换，设λ为滤波器尺度，多尺度形态学分析下的结构元素定义为

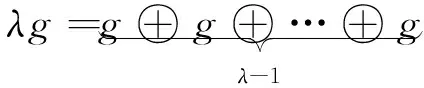
(11)

因此MCFH的多尺度定义为

fMCFH(f(n))=f(n)-[μ1AC&O(f(n))λg+

μ2ACO&OC(f(n))λg]

(12)

1.3 MCFHT性质分析

在滚动轴承运转过程中，损伤点撞击与其相接触的其他元件引起振动，表现为冲击激励产生的减幅振荡特征。通过模拟轴承外圈故障产生的冲击振动信号，我们可以验证MCFHT形态学算子的滤波性能，具体模型为

(13)

式中：振动幅值A=2；阻尼系数ζ=450；脉冲诱发的共振频率fn=1 500 Hz；采样频率fs=12 000 Hz；采样点数N=8 192；故障频率fm=120 Hz。图1为外圈故障冲击信号波形(截取两个周期)，表现为以fm为周期的指数衰减高频振荡。s2(t)为模拟风机叶片，轴和齿轮等部件产生的离散谐波分量，f1=50 Hz，f2=70 Hz。

使用MCFHT形态学算子处理故障模型中s1和s2的叠加信号，如图2中的虚线部分，s1脉冲成分被s2中的低频谐波波动干扰而发生变形。以长度为6的扁平型结构元素为例，应用MCFHT处理后结果显示为图2中实线信号，指数衰减高频振荡信号被从叠加信号中成功提取出来，信号故障冲击特征得以恢复，说明了MCFHT提取脉冲特征的有效性。

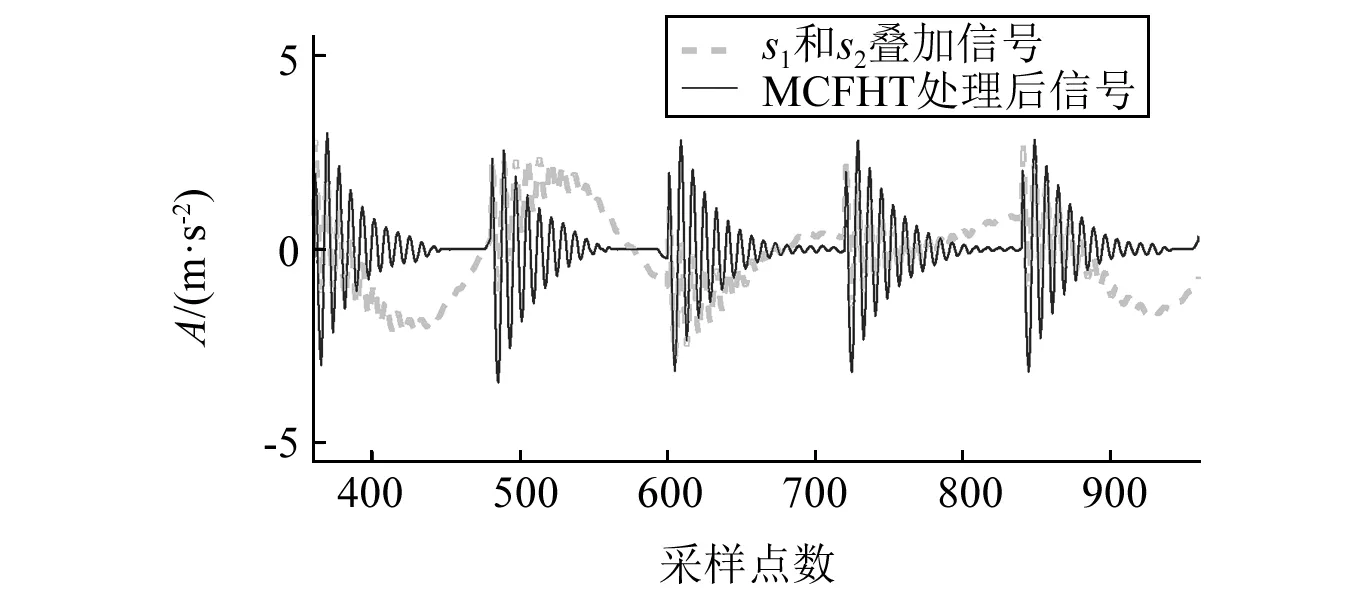
图2 MCFHT算子处理结果Fig.2 Filter result of MCFHT

为了理解MCFHT变换在振动信号处理中的工作机理，更好的利用其滤波性能，使用文献[16]中提到的非线性滤波器频率响应方法(单侧正弦模型)进行分析。仍采用扁平型结构元素，计算了MCFHT在不同尺度下的幅值频率响应，挑选尺度λ分别为1,2,3,5,8,16,32的情况，如图3所示，幅值为0.707时对应的归一化频率即为截止频率。图中观察发现MCFHT变换具有清晰的高通特性，并随着尺度λ增加，滤波截止频率逐渐减小，即通带范围加宽，当尺度λ为32时，幅值为0.707对应的归一化截止频率最小。因此结果表明MCFHT变换可以抵消低频谐波干扰，提取出故障特征。同时通过定量分析图3中滤波尺度对MCFHT变换频率响应的影响，也表明不同大小的滤波尺度意味着不同通带宽度的滤波器，通带太宽滤波后存在的带内噪声成分仍然较多；通带太窄则容易同时将故障脉冲滤除或削弱，因此滤波尺度在很大程度上影响MCFHT的滤波结果。上述分析表明，选择一个与实际故障特性匹配的滤波尺度至关重要。

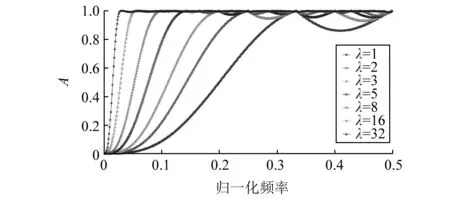
图3 MCFHT不同尺度幅频响应Fig.3 Magnitude-frequency characteristic of MCFHT with different SE scales

2 形态学综合顶帽变换滤波尺度选择

结构元素的选择对形态学变换的结果也起着较大的作用，常用的结构元素除了上述提到的扁平型，还有三角形以及正弦形等。其中，扁平型结构元素结构简单，计算效率高，能够避免信号幅值改变的影响，因此，本文后续研究均选用扁平结构元素进行处理，之后确定合适的滤波尺度。扁平结构元素的特点是扁平形状、零高度和特定长度，其长度L= 3代表最简单的形式{0 0 0}，此时形态学滤波尺度λ=1(λ=L-2)，因此选择最佳长度L成为确定滤波尺度的关键所在。而目前关于选择滤波尺度的研究中，很少有标准的选取原则，若按照经验取值，会增加许多主观因素，不能得到最佳滤波效果，难以适用不同应用场合。此外，近些年提出了一些利用寻优算法从给定较大尺度范围中搜索最优尺度，虽有一定通用性，但增加了成倍的运算量，不利于实际应用。针对尺度选择的盲目性，需要研究一种有效的滤波尺度确定方法。

图4为实际采集振动信号的部分细节，可以发现在高频振动信号细节中，尽管由于噪声干扰发生变形，但是指数衰减振荡对应的频率基本没有改变。以此为出发点，研究信号一段波形中峰峰值间隔采样点数来确定MCFHT滤波尺度大小，可以较好的贴合原信号振动衰减特征，对有效提取周期衰减脉冲序列奠定基础。不过当信号中噪声污染越严重时，参与选择的峰值必然会越多，其峰值间隔点势必会变小，将使取得的结构元素长度偏小，弱化由故障特征确定尺度大小的意义。为此，本文考虑在求峰值之间间隔点数的过程中，使用信号正峰值的均值作为阈值线，如图4中虚线所示。筛选保留大于该阈值线的峰值点，剔除小于该阈值线的峰值点，从而有效解决干扰污染严重时的问题。

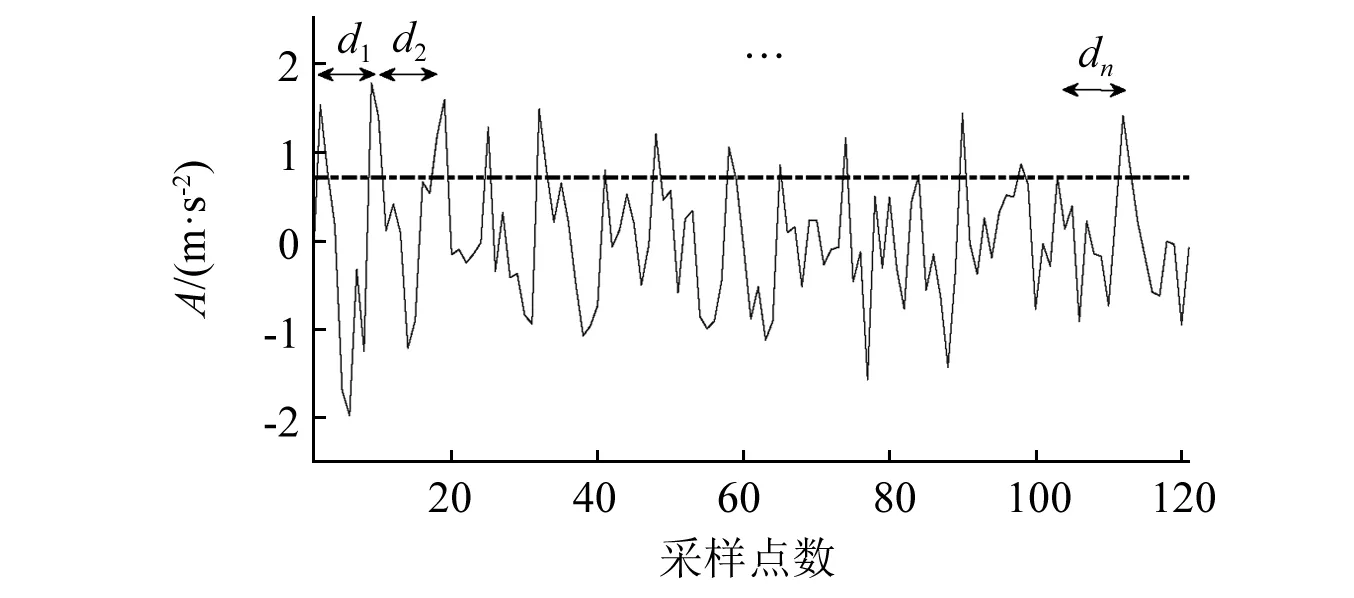
图4 振动信号的部分细节Fig.4 Local waveform of vibration signal

综合以上分析，本文提出尺度选择标准：即以信号所有正峰值点的均值作为阈值线，实现尺度选择。之所以这样选择，原因分析如下：信号中所有正峰值点求得的均值(阈值线)可代表噪声峰值与故障脉冲峰值的均值，一般情况下噪声成分幅值小于故障脉冲，处于阈值线之下，因此该阈值线可以将噪声与故障脉冲区分开。从而筛选出大于阈值线的正峰值点更多是故障脉冲点，此时计算相邻峰值采样点数则可视为合理的故障脉冲间隔。确定MCFHT变换结构元素长度的过程可总结为如下步骤，计算示例如图5所示。

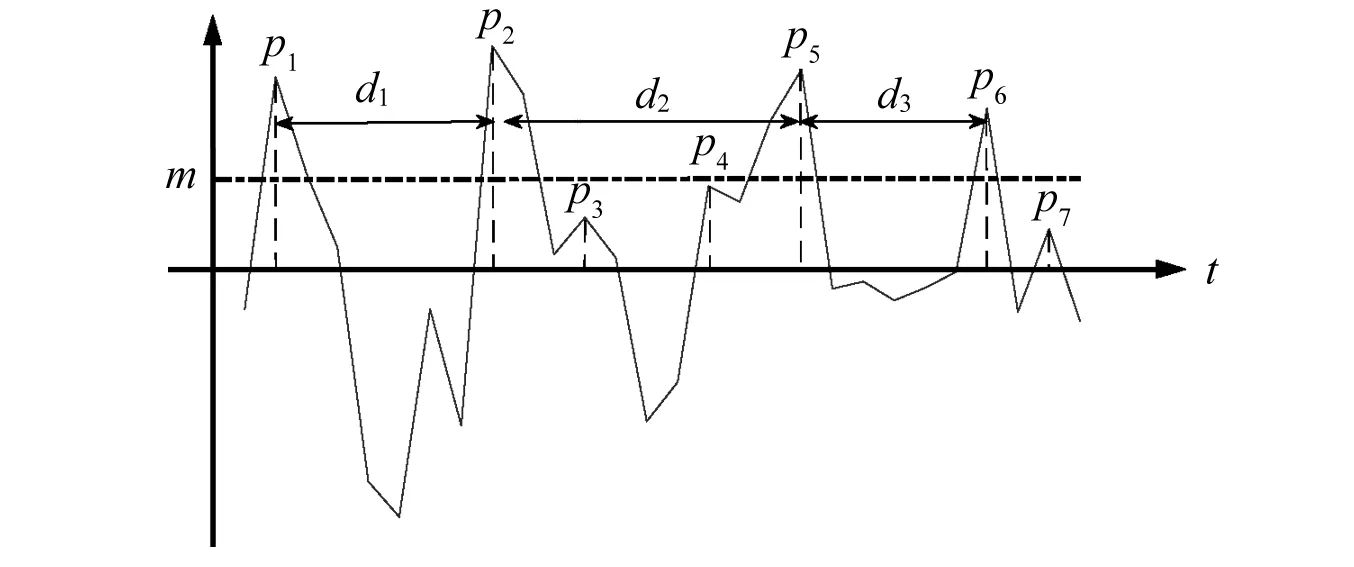
图5 信号正峰值筛选示例图Fig.5 Sample diagram of signal positive peak selection

步骤1首先对振动信号f(n)进行零均值化处理，得到y(n)={yn|n=1,2,…,N}。

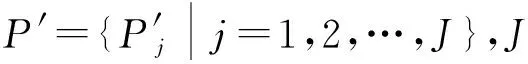
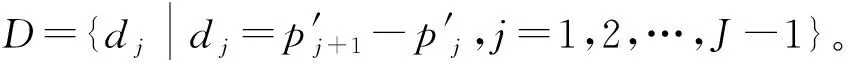
步骤4求J-1个dj的均值，作为振荡衰减间隔fs/fn的估计，即结构元素长度。

如图5示例所示，给定一段信号y(n)，其正峰值点为{p1,p2,p3,p4,p5,p6,p7}，取所有正峰值点的均值m作为阈值，将小于m的正峰值点{p3,p4,p7}认为是混入的噪声成分，大于m的正峰值点{p1,p2,p5,p6}认为是y(n)中的故障脉冲成分，由{p1,p2,p5,p6}对应的横坐标计算相邻点间的距离{d1,d2,d3}，并通过三个间隔的均值得到结构元素的长度，使用MCFHT变换得到信号y(n)的形态学滤波结果。上述结构元素自适应策略与轴承状态直接相关，体现着轴承故障征兆信息，获得的滤波结果更为合理，而且选择过程运算量小，不需要繁琐的寻优过程。具体滤波效果及比较参见后续实验部分。

3 改进的包络导数能量算子

尽管MCFHT运算能有效提取故障脉冲成分，但被其覆盖的带内干扰频率无法完全消除，为了提升信号信噪比，突出滚动轴承故障冲击，本文提出一种改进的包络导数能量算子进一步增强MCFHT滤波后结果。

常规的包络导数能量算子在直接应用时存在一些问题，如抗噪能力不强，主频与倍频在频谱中不够清晰。自相关运算具有一定降噪特性，因为噪声信号的自相关运算由时延的变大很快趋于零，并且不改变待处理信号的调制特性，此外Shannon熵函数能够抑制耦合调制产生的边频簇幅值，因此本文提出先采用自相关运算处理形态学滤波后信号，增强常规包络导数能量算子的抗噪能力，之后使用Shannon熵函数加强主导频率与倍频，使频谱更加纯净。改进后的包络导数能量算子具体分析如下。

对于MCFHT形态学滤波后信号x(t)，可通过解析信号定义为

X(t)=x(t)+jH[x(t)]=Aejφ(t)

(14)

式中,H[x(t)]为x(t)的包络。

一般而言，瞬时能量由信号的幅值平方计算

S[x(t)]=|X(t)|2+|x(t)+jH[x(t)]|2

(15)

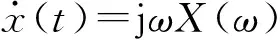
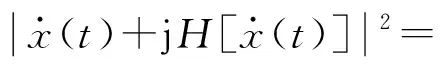
(16)

包络导数能量算子具有检测信号的瞬态变化，突出信号冲击成分的优势，但其抗噪能力不强，为此我们需要对其先进行自相关函数，以便增强其抗噪能力。

x(n)为待分析离散信号，其自相关函数可表示为

rxx(n)=E[x(n)x*(n+l)],l=0,1,2,…,N-1

(17)

式中，l为时间延迟。

由式(16)得到自相关包络导数能量算子的离散形式为

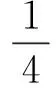
rxx(n-1)+Hxx(n+1)+Hxx(n-1)]

(18)

式中,Hxx为rxx(n)的包络。

接下来我们使用Shannon熵函数增强自相关包络导数能量谱，以使频谱更纯净，即

(19)

式中：n=0,1,2,…,N;σ为Γ[rxx(n)]的标准差。

自相关包络导数能量谱通过熵函数处理后，增强了幅值大于标准差σ的成分，削弱了幅值小于标准差σ的成分。

4 一种增强型的形态学滤波风电机组滚动轴承故障诊断方法

4.1 故障诊断流程

为提取风电机组传动链滚动轴承微弱故障特征，降低信号中谐波和噪声干扰，本文构造一种新的MCFHT形态学算子进行滤波，并根据脉冲信号振荡特征提出一种自适应尺度选择算法，该算法克服了形态学滤波尺度选择的主观性，避免尺度选择不当存在的隐患，相比于利用优化算法寻找最优尺度方法即保证了提取效果，又节省了时间成本。原信号通过MCFHT形态学算子滤波后，虽然能够提取故障信号中脉冲成分，提高信号信噪比，并有不错的抑制噪声效果，但滤波后的带内残余噪声难以有效去除，频谱分析时故障特征频率并不十分突出。故而结合一种改进的包络导数能量算子增强形态学滤波结果，从故障脉冲提取、去除带内干扰和特征增强三个角度共同作用，对故障信号进行深层次挖掘。综上，本文提出了一种增强型的形态学滤波风电机组滚动轴承故障诊断新方法，诊断流程如图6所示，具体步骤如下：

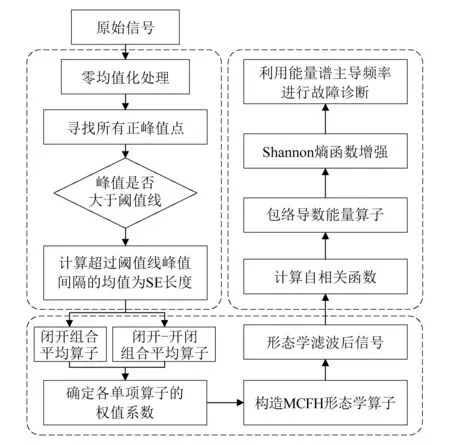
图6 故障诊断方法流程图Fig.6 Flow chart of fault diagnosis

步骤1获取信号所有正峰值点，利用正峰值点的均值作为阈值线，超过阈值线的正峰值计算其采样点间隔的均值，以此自适应确定结构元素长度。

步骤2使用得到的结构元素长度对原信号进行闭开组合平均和闭开-开闭组合平均运算，并计算两次结果与原信号的相关系数，以此确定各单项算子的权值系数，结合顶帽变换思想，构造MCFHT形态学算子，得到MCFHT滤波后信号。

步骤3计算滤波后信号的自相关函数，削减带内噪声，在此基础上用包络导数能量算子突出故障冲击成分，利用熵函数抑制边频簇幅值。

步骤4通过能量谱中主导特征频率成分与故障特征频率理论值进行对比分析，判断发生的故障类型。

4.2 仿真分析

为验证本文所提方法提取轴承故障周期性脉冲信号的有效性，仍采用式(13)中使用的轴承仿真模型，添加信噪比SNR=-12 dB的白噪声，仿真混合信号如下图7(a)所示，为了清楚呈现时域波形，图中仅给出部分采样时刻信号。其频谱如图7(b)所示，从图7(b)中可以看到原振动信号频谱图中仅含有谐波频率50 Hz和70 Hz，检测不到故障频率120 Hz。

图7 故障仿真信号时域波形及频谱Fig.7 Temporal waveform and amplitude spectrum of simulated signal

为了提取故障相关特征(120 Hz及其倍频)，抑制干扰频率(50 Hz，70 Hz和噪声)，首先使用MCFHT形态学滤波器处理原信号。其中AC&O(f(n))和ACO&OC(f(n))

两次滤波结果与原信号的相关系数r1,r2分别为0.51,0.74，计算得到两个单项滤波器的系数μ1,μ2分别为0.59,0.41。在自适应选择结构元素长度过程中，利用4.1节中的步骤1，选取的扁平型结构元素长度为9，根据这些参数滤波后结果如图8所示。图8(a)为时域图，可以看到有效减少了谐波趋势的干扰，冲击成分比较明显。图8(b)为滤波后信号频谱，故障频率处的峰值谱线得以突出，说明形态学滤波的有效性。但频谱中仍可看到较多的噪声频率，易对信号故障特征的识别造成干扰。

因此继续采用上述改进的包络导数能量算子对信号进一步降噪和脉冲冲击成分增强。如图9所示，与图8(b)相比，能量谱更加清晰干净，50 Hz和70 Hz的干扰谐波频率被滤除，噪声频率得到有效抑制，检测到故障特征频率fm及其倍频2fm～4fm处幅值更加突出，可以据此准确判定轴承损伤类型。

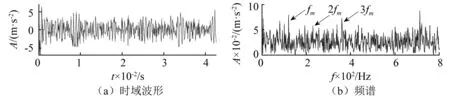
图8 MCFHT形态算子滤波后结果(L=9)Fig.8 Result of MCFHT morphological filtering(L=9)

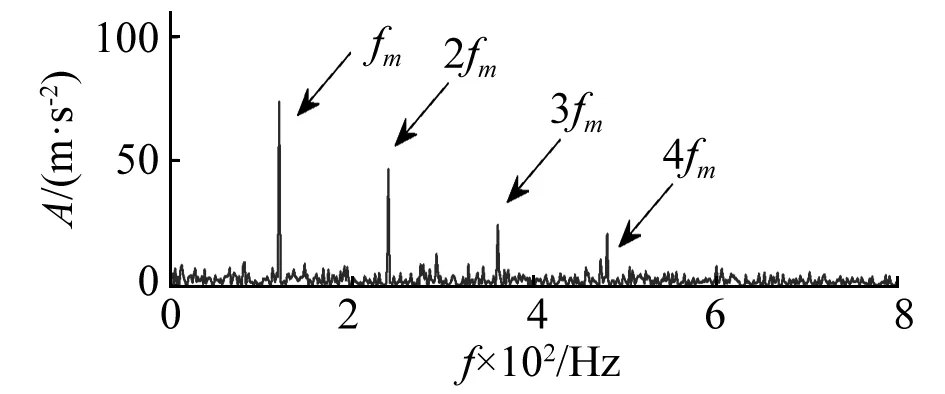
图9 增强型形态学滤波能量谱(L=9)Fig.9 Energy spectrum of the proposed enhanced morphological filtering(L=9)

为了直观地分析比较所提增强型形态学滤波的效果，给出以下三种实验情况。①验证本文采用阈值线筛选正峰值点的作用。由信号所有正峰值点间隔的均值计算得到结构元素长度，并用增强型形态学滤波，此时结构元素长度为5，结果见图10(a)，可以看到只有故障特征频率fm处谱线突出，无法获取其倍频谱线信息，故而未进行筛选得到的尺度降低了增强型形态学滤波的效果；②验证改进后包络导数能量算子的提升作用，图10(b)展示了经MCFHT算子滤波后应用常规包络导数能量算子增强的结果，可以发现，虽然fm倍频处幅值得到了一定加强，但信号中许多杂频干扰无法消除，故障特征不够清晰；③验证使用改进后包络导数能量算子的合理性，用传统的Teager能量算子[17]对图8(a)信号进行处理，能量谱如图10(c)所示，同样发现故障频率fm及其倍频受杂频干扰，频带内部噪声较多，且干扰频率幅值比较高，由此可以证明本文所提增强型形态学滤波器在噪声污染与谐波干扰环境下对信号中故障特征更好的提取能力。

图10 三种比较分析结果Fig.10 Results of three comparison methods

继续使用余建波等提出的一种形态学平均组合差值算子(average combination difference morphological filter，ACDIF)处理图7(a)信号，结构元素长度通过该文提出的Teager能量峭度的大小来选择，确定长度为12，滤波结果及其频谱如图11所示，虽然故障频率fm及其倍频处幅值比较突出，但是两个谐波分量频率点幅值也很明显，ACDIF虽能提取故障脉冲，抑制一定程度的背景噪声，但无法消除谐波干扰，会对诊断结果造成影响，据此可以进一步证明本文方法的有效性和优越性。

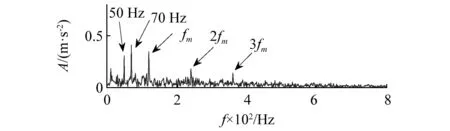
图11 ACDIF形态学算子处理结果Fig.11 Result of ACDIF morphological filtering

4.3 真实风机

为了进一步验证本文所提方法在实际风电机组轴承故障诊断中的有效性与可行性，采用从内蒙古自治区翁贡乌拉风电场测取的风电机组传动链轴承故障振动信号进行分析处理，风机型号为阳明1.5 MW风机。振动加速度传感器安装在风电机组驱动端，以此采集轴承信号。信号采样频率为26 kHz，轴承型号为6332MC3 SKF深沟球轴承。详细参数如表1所示，转速为1 882 r/min，外圈和内圈故障特征频率分别为fo=99.97 Hz和fi=150.97 Hz。

表1 滚动轴承6332MC3 SKF 基本参数Tab.1 Parameters of rolling element bearing 6332MC3 SKF

4.3.1 外圈故障

图12(a)，图12(b)分别为风电机组滚动轴承外圈故障信号时域图和频域图，从图12(b)看出，频谱中外圈故障特征频率及其倍频的幅值被各种干扰所淹没，难以识别故障特征。计算得到两个单项算子的权值系数μ1，μ2分别为0.73，0.27，根据结构元素自适应选择方法确定SE长度为6，利用MCFHT形态学滤波对外圈故障信号进行处理，得到如图13的滤波结果。相比于图12(a)，图13(a)中滤波后信号中的冲击成分更加明显，图13(b)频谱中也可以观察到轴承外圈故障特征频率及其倍频fo～3fo，但谱线并不十分突出，还残留冗余干扰成分。继续使用改进的包络导数能量算子抑制残余噪声，强化故障特征。能量谱如图14所示，噪声干扰频率成分明显减少，谱中清楚地提取了轴承外圈故障特征频率及3倍频成分。分析结果表明本文方法能够有效提取滚动轴承外圈故障特征。

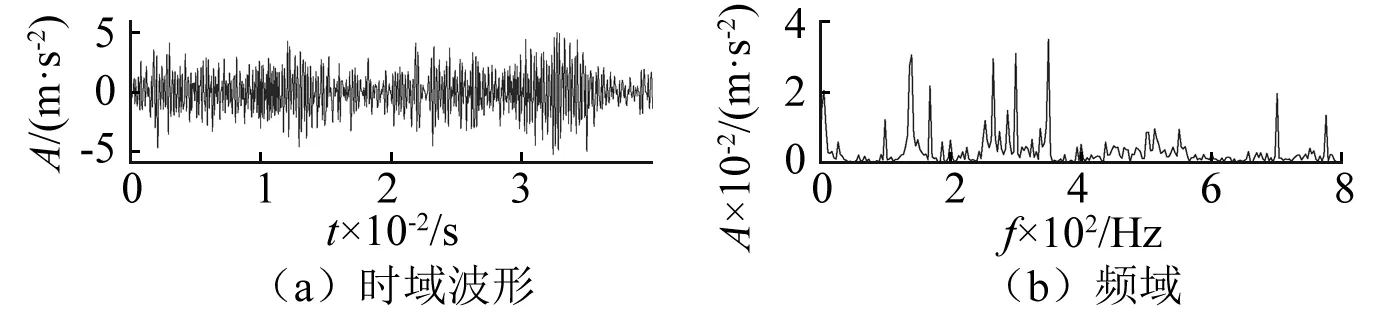
图12 风电机组轴承外圈故障时域波形及频谱Fig.12 Temporal waveform and amplitude spectrum of outer-race fault for wind turbine bearing

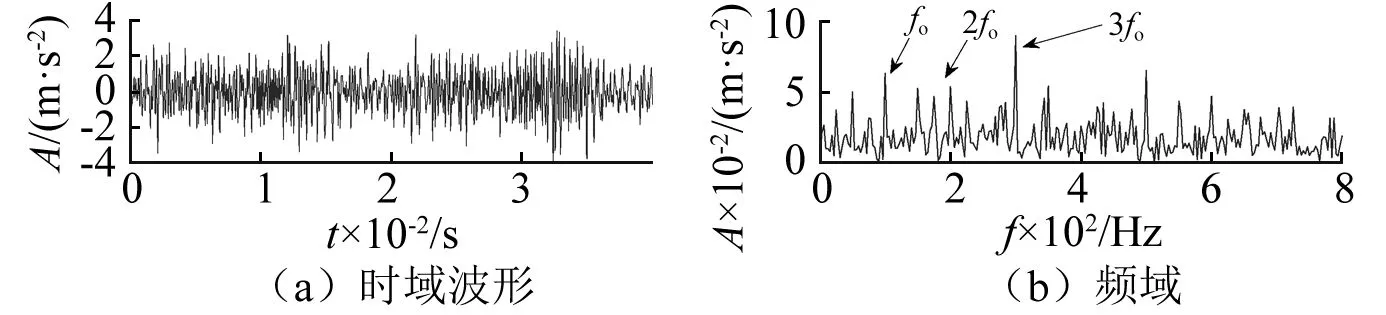
图13 MCFHT形态学算子滤波后结果(L=6)Fig.13 Result of MCFHT morphological filtering(L=6)

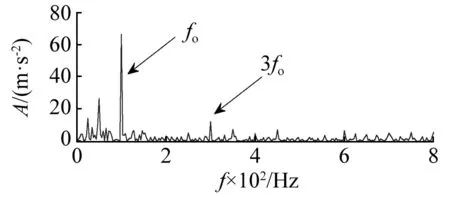
图14 增强型形态学滤波能量谱Fig.14 Energy spectrum of the proposed enhanced morphological filtering

图15为采用常规包络导数能量算子对MCFHT滤波后信号处理的结果，从中可以看出，虽然外圈故障频谱比较突出，但是一处低频干扰的幅值也很大，影响诊断结果。图16为使用ACDIF算子处理结果，同样被幅值较高的杂频所干扰。综上分析可以表明本文方法在提取风机振动信号中故障冲击序列，抑制其中谐波和背景噪声的有效性，也说明了在风电机组外圈故障诊断中的优越性。

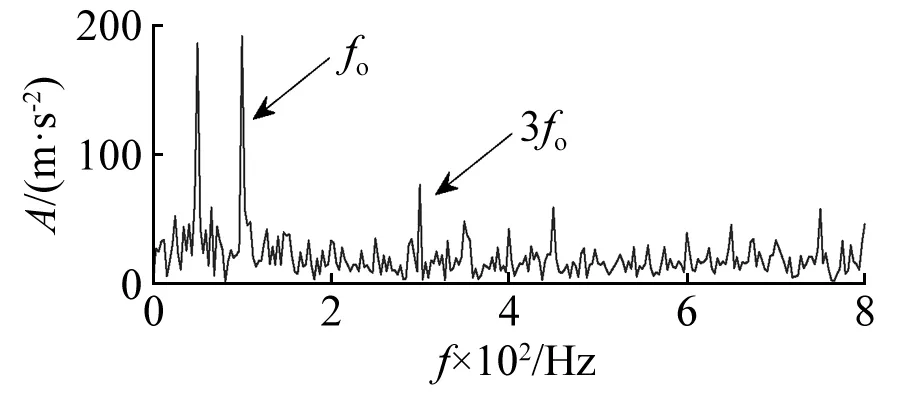
图15 形态学滤波后常规包络导数能量谱Fig.15 Energy spectrum of traditional envelope derivative operator after the MCFHT morphological filtering

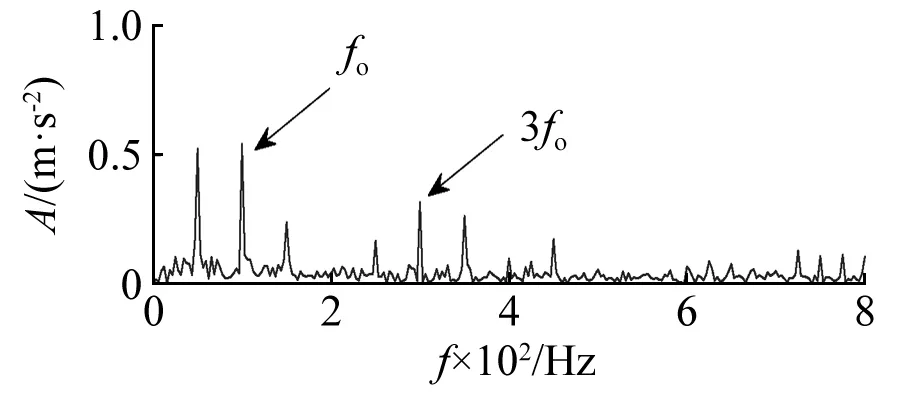
图16 ACDIF形态学算子处理结果Fig.16 Result of ACDIF morphological filtering

4.3.2 内圈故障

当风电机组轴承内圈发生故障时，采集到的时域波形如图17(a)所示，故障脉冲信号的周期特征比较微弱。图17(b)为故障信号的频谱图，由于实际工作环境中强噪声的干扰，从频域中观测到与故障特征相关的频率成分较少。

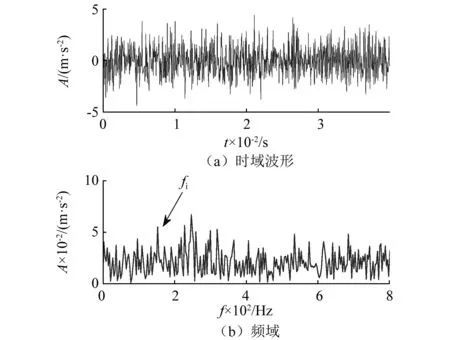
图17 风电机组轴承内圈故障时域波形及频谱Fig.17 Temporal waveform and amplitude spectrum of inner-race fault for wind turbine bearing

为了准确提取轴承内圈故障特征，按照上述相似步骤对内圈故障信号用增强型的形态学滤波器处理，计算得到μ1,μ2分别为0.64，0.36，结构元素长度为7，滤波后信号的能量谱如图18所示。可以直观的看出内圈故障特征频率及其多个倍频fi～4fi对应的谱线很容易分辨，说明有效提取了内圈故障脉冲，判断轴承内圈出现故障。同样给出常规包络导数能量算子处理结果，如图19所示，虽然能找到内圈故障特征频率及其2倍频，但幅值不够突出，提取效果欠佳。ACDIF形态学算子处理结果如图20所示，频谱中无关频率成分较多，很难确定故障频率。以上对比表明本文所提方法对风电机组轴承内圈故障冲击提取和故障诊断的优越性。

图18 增强型形态学滤波能量谱(L=7)Fig.18 Energy spectrum of the proposed enhanced morphological filtering(L=7)

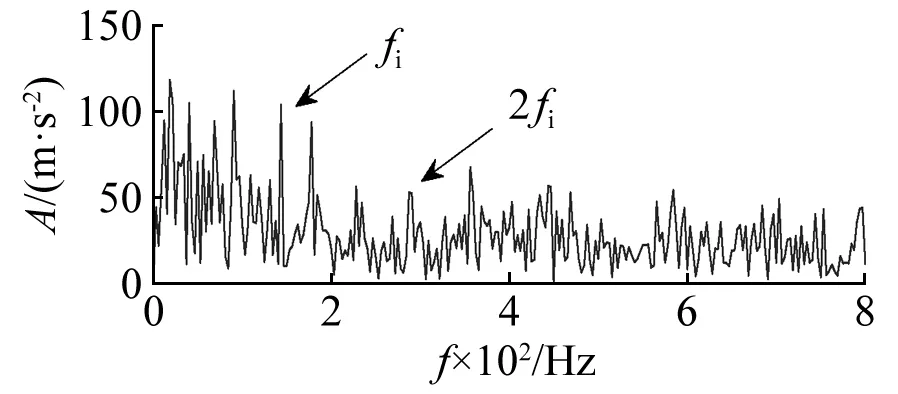
图19 形态学滤波后常规包络导数能量谱Fig.19 Energy spectrum of traditional envelope derivative operator after the MCFHT morphological filtering

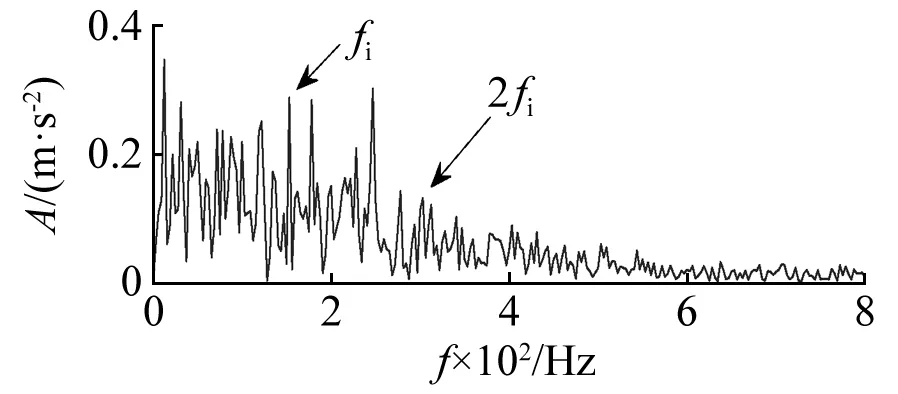
图20 ACDIF形态学算子处理结果Fig.20 Result of ACDIF morphological filtering

5 结 论

本文提出一种增强型的形态学滤波分析新方法，用于检测风电机组传动链滚动轴承故障。借鉴两种形态学平均滤波算子以及顶帽变换首先提出一种新的MCFHT形态学算子，可以有效提取故障信号中的脉冲成分，并通过非线性频率响应考察了MCFHT具有很好的高通特性，揭示其提取脉冲特征的能力。之后，由原故障信号的自身振动特性出发，以信号筛选后的正峰值相邻采样点间隔作为结构元素的长度，即形态学滤波尺度，既保证了滤波效果，又节省了大量时间成本。最后利用一种改进的包络导数能量算子作为后置环节，去除MCFHT滤波后信号中存在的带内残余噪声，突出信号的冲击成分。分析比较结果表明，所提出的增强型形态学滤波方法能够消减各种干扰，有效提取轴承振动信号的脉冲特征，具有更好的故障检测能力。