基于多模主曲线法估计韧脆转变区间热影响区断裂韧度

胡馨丹，惠 虎，张亚林，周忠强

(华东理工大学 机械与动力工程学院，上海 200237)

0 引言

当考虑脆性断裂时，金属材料常被认为不是连续体。如脆性断裂局部法中就是将裂纹前缘的材料定义为断裂过程区，区域内又分为不同的单元体。金属材料中包含位错堆积、晶界与亚晶界、沉淀物和夹杂物，这些微观不均质常是引发低温脆断的原因[1]。对于宏观上均匀的材料，这种缺陷是随机分布的，从而使得材料在微观上具有不均匀性而宏观上是均匀的。在许多不同结构材料中，这种不均匀性通常称之为随机不均匀性。除此之外，还有其他不均匀性的类型，例如焊接接头的焊缝和焊接热影响区。由于焊接过程是一种快速升温和冷却的过程，根据峰值温度的由高到低，热影响区(HAZ)可以分为几个不同的组织区域，即：部分熔化区加过热区、正火区、不完全正火区、回火区。其中，过热区晶粒极其粗大且晶界和晶内化学成分和组织不均匀，是焊接接头的薄弱环节。若已知试样的取样位置以及测试了足够多的试样，则可以考虑这种确定性的不均匀性对材料韧性的影响。

主曲线法是由WALLIN等[2-3]提出的、仅通过测试少数试样得到一个参考温度T0就可以描述整个转变区间的断裂韧度的一种方法。其已被写入标准ASTM E1921中，并被各国的核电规范和结构完整性评价广泛使用。众多研究指出，当用于宏观非均质材料时，用于分析脆性断裂试验结果的标准主曲线法将不再适用[4-6]，标准主曲线法仅适用于宏观均质的材料。这限制了该方法的使用，直到2019版ASTM E1921增补了附录5中提及了多模主曲线法，是解决不均质材料韧性评估的一种潜在解决办法[7]。而我国有关这方面的研究还非常有限，主要是因为热影响区的范围很窄，很难取出有效试样。国际上有关断裂韧度的测试标准，仅有英国的BS 7448提及热影响区断裂韧度的测试，但仍然缺乏具体的取样手段和合格标准[7-11]。因而有必要开展不均质热影响区断裂韧度测试，并获取韧脆转变区间的韧性分布和特征温度T0，该研究对于建立不均质焊接接头的完整性设计和评价具有重要的意义。

本文以低温压力容器用钢SA738Gr.B埋弧焊焊接热影响区实测韧性数据为研究对象，分析标准主曲线法对于不均质材料的不足之处，并消化吸收2019版ASTM E1921标准中新增补的多模主曲线法，分析多模主曲线法分析过程，将复杂的数值求解过程通过编程实现；同时，对比研究标准主曲线法和多模主曲线法的预测结果。本文的研究方法和结论有助于解决不均质材料的性能评估，尤其对异种金属焊接接头的性能评估。

1 断裂韧度试验

1.1 试验材料

测试母材为核电用钢SA738Gr.B，标称厚度55 mm，交货状态为淬火加高温回火，根据ASME的要求，其化学成分、拉伸力学性能和冲击性能的试验值应分别符合表1～3中的要求。根据含碳量和合金含量，该钢为低合金钢。焊接采用埋弧自动焊，2块尺寸为55 mm×300 mm×600 mm材料作为焊接试板，在焊接之前通过机加工如图1所示的X坡口。焊接主要参数如表4所示，焊接采用多道焊且层间温度不低于200 ℃，焊接前的预热温度为120 ℃。

表1 SA738Gr.B钢的化学成分

表2 拉伸力学性能要求

表3 冲击性能要求

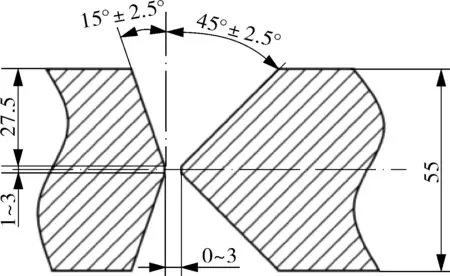
图1 焊接试板坡口结构示意

1.2 取样与测试

考虑到热影响区的非均质性，为了获取可靠的韧性评估，需要测试足够多的试样。本文依照图2的取样方式，提取26个试样进行试验，试样采用0.5T的C(T)试样。HAZ的宽度约2 mm，取样时让整个裂纹平面置于热影响区薄片层内，裂纹扩展方向沿着焊接线的方向(见图2(b))。断裂韧度试验包含两个部分：疲劳试验预制裂纹和低温环境下的断裂试验。通过线切割的方式预制宽度大约2 mm的尖锐疲劳裂纹，使裂纹尖端与加载孔的纵向间距和试样宽度的比值在0.45～0.7标准要求值以内。试验温度设定为-120 ℃和-130 ℃，使用液氮喷淋的方式进行制冷，PID控制器全程控制温度在目标温度±3 ℃以内。

(a)取样位置及局部放大

(b)0.5T-C(T)试样结构尺寸

2 标准主曲线法分析过程

主曲线法的基础是1984年芬兰科学家WALLIN[10]关于断裂韧度在韧脆转变区内的分散性的研究，而后在1997年名为“确定铁素体钢韧脆转变区参考温度的标准试验方法”的标准被提出，该标准即是主曲线法的试验操作和数据分析的规范[11]。

主曲线法是基于最弱链理论，该理论认为在适用范围内的材料发生断裂主要由于裂纹萌生，并且它们的韧脆转变区内任意温度下的断裂韧度的累积失效概率可以用同一个三参数威布尔分布函数表述：

(1)

式中，Pf为累积失效概率；B为试样厚度，mm;B0为参考试样的厚度，mm,通常将厚度为1 in(25.4 mm)的试样称为1T试样;KJc为弹塑性断裂韧度，MPa·m1/2；Kmin为门槛断裂韧度，MPa·m1/2，通常取Kmin=20 MPa·m1/2；K0为尺度参量，为Pf=63.2%时的KJc值;m为形状系数，经过大量试验数据得出的试验值为4，后文为威布尔斜率。

门槛断裂韧度Kmin，WALLIN提出将它的值固定为20 MPa·m1/2,与温度和试样的厚度无关[2]。在计算参考温度T0时，不同尺寸的断裂韧度试样都需要通过尺寸调整变为标准试样厚度的断裂韧度值，其换算公式见式(2)，其中B0=25 mm，厚度B为实际测试试样的标称厚度，与侧面开槽无关。

K25.4 mm=Kmin+(KJc-Kmin)(B/B0)1/4

(2)

值得注意的是,在韧性较低的下平台，上式可能不够准确。因为该模型基于最弱链假定，即认为脆性断裂是由裂纹的启裂控制的[12]。在较低的温度下，启裂准则将不再是主要控制断裂的准则，断裂主要是由裂纹在晶界之间扩展的难易控制，这取决于晶界的结合强弱。在这种情况下，没有统一的尺寸效应，断裂韧度的分布变化程度较小也不符合三参数威布尔分布[13]。本文主要研究韧脆转变区间断裂韧度的分布情况，因而通过有限的试样得到转变区间的韧性分布是有价值的，公式(1)(2)也是有效的。对于结构钢，WALLIN[4]基于大量的统计分析，得到一条经验性的结论，即有一条表述断裂韧度-温度相关性的主曲线，可以通过公式(3)定义。对应于1T厚度的标准试样，若平均断裂韧度能到100 MPa·m1/2，此时的测试温度即为参考温度T0。该参考温度是材料的宏观断裂性能的表征参数。

K0=31+77exp{0.019(T-T0)}

(3)

ASTM E1921提供了两种确定参考温度T0的方法，即单温度法和多温度法。对于单温度法，需要根据下式估算威布尔分布尺度参数K0：

(4)

式中，KJc(i)为所有有效和无效试样转换成1T标准试样的KJc值。

将尺度参数K0代入下式可得中值断裂韧度KJc(med)：

KJc(med)=(K0-20)(ln2)1/4+20

(5)

将KJc(med)代入下式得到参考温度T0：

(6)

对于多温度法，需要通过编程将不同温度下的KJc(1T)代入公式(7)迭代求解T0。

(7)

式中，δi为克罗地亚检查常数，当KJc(i)有效，δi=1，当KJc(i)无效，δi=0;Ti为对应于各KJc(i)的试验温度，℃。

使用获得的参考温度T0来建立材料在不同失效概率下的断裂韧性与温度之间的关系，可以用下式计算：

KJc(Pf)=20+[-ln(1-Pf)]1/4[11+77

×exp{0.019(Ti-T0)}]

(8)

3 多模主曲线法分析过程

多模主曲线法适用于表征宏观不均质材料的参考温度，其中假定不均匀性非常大，以至于可以把T0看成随机变量，并服从高斯分布[14]。高斯分布可完全由两个参数定义：总体的平均参考温度(Tm)和围绕平均值的标准偏差(σTm)。要执行此评估，通常要求在[Tm-50 ℃，Tm+50 ℃]的温度区间内有20个数据点。以下为估计这两个参数的极大似然估计步骤。

假设随机变量T0服从由均值Tm和标准偏差σTm表征的高斯分布。在这种情况下，T0的概率密度函数为：

(9)

式中,τ0为计算累积失效和存活概率密度的温度。

Tm和σTm使用适当的求解算法确定，该算法可使公式(10)给出的似然对数值最大化。

(10)

式中,N为被测试样数量;fi为累积失效概率密度函数，由公式(11)得出;Si为累积存活概率密度函数，由公式(12)得出。

(11)

(12)

其中，条件失效概率密度函数fτ0(i)表达式见式(13)，与标准主曲线法中的表达式是一致的。

(13)

条件存活概率密度函数Sτ0(i)表达式见式(14)，与标准主曲线法中的表达式是一致的。

(14)

式中，Kτ0(Ti)为在试验温度Ti，以计算累积失效和存活概率密度的温度τ0表征的一个断裂韧度数据样本的威布尔尺度参量，由公式(15)给出。

(15)

当使用数值方法来计算公式(11)(12)中的无穷积分时，在-200 ℃<τ0<200 ℃范围内进行评估，通常会提供足够的精度。对于多模主曲线法容许失效曲线的确定，在有效温度范围内的每个温度，可以找到满足公式(16)中的KJc(Pf)值。

(16)

4 结果与讨论

4.1 标准主曲线法分析结果

通过试验测得SA738Gr.B埋弧焊焊接热影响区韧性数据的有效试验结果如表5所示。为了检验主曲线法对不均质材料的适用性，对试验结果使用单温度法和多温度法进行处理，其中-130 ℃下的断裂韧度采用单温度法，-130 ℃和-120 ℃的断裂韧度采用多温度法。依据第2节主曲线法的分析过程，可以得到热影响区的断裂韧度的分布情况，如图3所示。其中用标准主曲线法测得的参考温度用TOMC表示，分别为-137.4 ℃和-136.5 ℃，二者几乎相当。但是，从图3可看出，热影响区的断裂韧度有较宽的分散带，并且有部分数据点落在了5%和95%容许失效边界曲线之外。这意味着标准主曲线法用于表征不均质材料韧脆转变区间的断裂韧度可能会存在问题。下文中将对这一问题进行具体分析。

主曲线法的理论基础之一，是认为铁素体钢在韧脆转变区任一温度下的断裂韧性的分布符合形状系数为4、门槛值Kmin为20 MPa·m1/2的三参数威布尔分布公式(1)，将其整理后两边取双ln对数，经线性化的公式如下：

(17)

表5 断裂韧度试验结果

在以lnln(1-Pf)为纵坐标和以ln(KJc-20)为横坐标的坐标图上，所有断裂韧性数据理应均匀地分布在斜率为4直线的两侧。将本文在-130 ℃下所测得的SA738Gr.B埋弧焊焊接热影响区韧性数据绘制在图4坐标图内，图中试验数据点的累积失效概率Pf按下式计算:

(18)

式中,i为断裂韧性值按从小到大排序后的序号；N为试验数据断裂韧性数据总数。

从图4可以看出，实测数据和标准主曲线法经线性化的三参数威布尔分布的相关性较差，尤其在图示虚线框内，数据点严重偏离线性化直线。这说明，三参数威布尔分布不能够准确表征不均质材料的韧性分布。而且在图4中的阴影区域，对应于中低韧性区间，数据点在整个直线的左侧，这说明生搬硬套使用主曲线法会高估热影响区的断裂韧度，造成危险的估计。同样的，测试数据的实际拟合曲线的斜率为2.7和理论中的斜率4也不相符合。从上述分析可以看到，主曲线法对SA738Gr.B热影响区的断裂韧度评估具有局限性。

(a)单温度法 (b)多温度法

图4 断裂韧性数据的三参数威布尔分布

4.2 多模主曲线法分析结果

对HAZ这种典型不均质的区域，不同的热作用导致HAZ测试结果差别很大。由于淬硬的马氏体组织的存在，位于过热区的试样可能会产生极低的断裂韧度测试数值；位于正火区和回火区的试样由于受热影响较小，通常韧性较好，会产生较高的断裂韧度测试数值。若将HAZ不同区域的参考温度T0看成一个随机变量是合适的，后续将结合试验结果进一步研究多模主曲线法对不均质HAZ韧性评估的适应性。

由于材料不均匀性的影响，多模主曲线法比标准主线法更复杂，本文解释了三参数威布尔分布在分析断裂韧性数据时会带来一定的偏差。与标准主线法方法类似，但多模主曲线法将三参数威布尔分布改进为多模分布，可以通过基于试验数据的最大似然估计方法来估计相关参数，平均参考温度Tm和标准偏差σTm、K0和(T-T0)的统计依据保持不变，可见标准主曲线法和多模主曲线法的联系和区别是：它们预测曲线的形状一致，但前者采用的是威布尔分布，后者采用的是多模分布。大多数研究表明，只要有足够的试验数据，多模主曲线法是有效的，通常建议不少于20个数据点用于极大似然估计。运用编程，求解合适的参数Tm和σTm，使公式(10)中的lnL最大。对-120 ℃和-130 ℃下的断裂韧度数据求解后可得：Tm=-128.4 ℃，σTm=17.1 ℃。

对于中值断裂韧度以及5%和95%的容许失效边界，可以用公式(9)～(16)确定。Pf=0.05时，确定为5%的失效概率曲线；Pf=0.95时，确定为95%的失效概率曲线。5%失效概率由KJc(0.05)表示，95%失效概率由KJc(0.95)表示。用公式(16)迭代法测定了测试温度在-200 ℃

与标准主曲线法相似，多模主曲线法获得SA738Gr.B钢的韧脆转变温度T0的95%和5%上下边界的失效概率图如图5所示。通过多模主曲线法获得的平均参考温度Tm=-128.4 ℃，相比之下，这个结果高于标准主曲线法的参考温度。在数据包络性方面，多模主曲线法的5%和95%上下边界曲线更宽，因而可以容纳由不均质所导致的分散性过高或者过低的数据点。不仅如此，在重要结构的完整性评估中，如核电、高压或超高压容器中，常用5%累积失效概率下的断裂韧度作为材料性能的输入值。多模主曲线法会产生比较保守的低韧性估计(如图5所示)，相较于标准主曲线法，多模主曲线法5%的预测曲线更低。因而，多模主曲线法是一种适用于评估不均质材料断裂韧度的方法。

表6 多模主曲线法的中值断裂韧度和5%，95%容许失效边界值

图5 多模下95%和5%上下边界的失效概率图

本文测试的数据显示了新版ASTM E1921—2019不均匀性附录的价值，当标准主曲线法使用受限制时，它提供的分析方法和公差范围适用于表征不均质铁素体钢的韧性评估。当评价焊缝和热影响区转变区间的性能时，尤其对于异种金属焊接接头，提供了切实可行的解决办法。运用多模主曲线法并联合容许失效边界曲线，可以概率性地应用测试数据来评估厚壁压力容器和焊接件的完整性。

5 结论

本文以55 mm厚SA738Gr.B钢埋弧焊热影响区实测韧性数据为研究对象，分析了标准主曲线法不足之处，并探讨了多模主曲线法的分析过程，用MTLAB编程实现复杂的数据处理过程，对比研究了标准主曲线法和多模主曲线法的预测结果。主要测试结果和结论如下。

(1)通过标准主曲线法的单温度法和多温度法得到SA738Gr.B热影响区的参考温度分别为-137.4 ℃和-136.5 ℃；多模主曲线法获得的参考温度为-128.4 ℃，比标准主曲线法高出约8～9 ℃。此外，多模主曲线法可以容纳热影响区过大的分散性，且可以得到更为保守的5%容许失效边界曲线。因而，标准多模主曲线法适用于表征不均质材料的断裂韧度，且能提供相对保守的预测结果。

(2)标准主曲线法估计的准确性与采样位置密切相关。由于材料的不均匀性，实测的威布尔斜率2.7比理论值4小1.3。通常，不均匀性导致测试结果的断裂韧性分布偏离三参数威布尔分布，并高估了材料的韧性。

(3)对于厚壁结构钢和焊接接头，很难做到绝对均匀。因而，多模主曲线法更符合实际情况，可成功地描述微观结构不均匀的焊接热影响区转变区间的断裂韧度，但结果的准确性直接与数据样本的大小有关。

本文测试了26个数据能得到较为稳定的结果。但实际工程应用，如此数量的测试很难实现，因而综合数据结果的可靠度和样本容量的大小，确定合适的数据样本的大小至关重要。这一部分内容笔者将在下一篇文章中给出具体的说明。