水平井油水混合物准三维非稳态渗流传质研究*

迟 杰，张隆源，张梦飞

（中国石油大学 胜利学院 a.基础科学学院；b.机械与控制工程学院，山东 东营257061）

在最近的几十年中，数学模型已成为决定油气田分析，维护和开发决策的主要工具。基于有关沉积物的具体特征来寻找石油油水、油气两相传质传热等问题的解决方案，可以长期预测石油产量，并评估维持油藏压力的措施和其他提高采油率的措施的有效性[1,2]。黄志江等[3]研究油水两相流在颗粒多孔介质中的流动阻力特性, 建立了颗粒填充多孔介质通道中油水流动过程的计算模型。宋红伟等[4]对低流量水平井油水两相分层流速度场进行数值模拟取得很好的应用效果。谭刚等[5]讨论了油水两相流压降和持水率与滑移的影响因素, 并对今后的发展和下一步的研究方向提出了建议。刘静等[6]低渗透二维两相流的数值模拟，进一步丰富了变流体物性水驱渗流数学模型。徐冰[7]综合考虑裂缝内法向渗透压力、裂缝渗透系数的相互作用和岩体中渗透压力、渗流体积力、岩体渗透系数的相互作用，建立了压裂渗滤强化采油条件下流固耦合裂缝扩展三维数学模型。刘焯[8]创新地利用核磁共振测试,研究了压力梯度、注入倍数、渗透率、反向驱替这四个因素对微观油水赋存状况的影响。王建忠等[9]通过改善低渗透油藏的渗透率或者降低油水界面张力将是减小压力波动、利于生产的有效措施。

尽管如此，使用流体动力学模型的实践表明，数学模型的功能远远不能满足解决与现场开发相关的重要生产问题时出现的需求[10]。特别是适用于复杂的非常规领域中开发过程进行建模。迫切需要解决的问题是构建用于计算粘性油田（尤其是水平井附近）的开发参数的计算模型。本文通过在自然半固定坐标系下建立动态计算网格的计算域离散化方法，尝试用半固定的自然网格计算两相传质的问题，并给出了所确定形状的流中相流量的解析表达式。以期该对水平井平行井系统的各种模型开发和应用提供参考。

1 方法论

用于计算油水混合物的非平稳渗流的方程组包括：

相连续性方程式（1）：

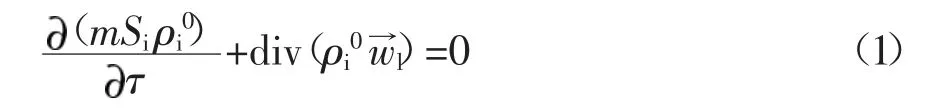
广义达西方程式（2）：

油水混合物内部能量平衡方程式（3）：

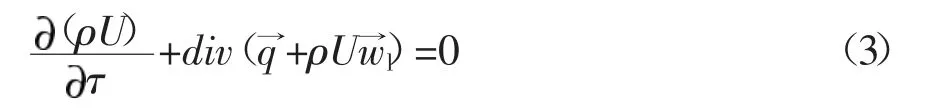
式中 div：散度公式；grad：梯度公式；τ：时间，s；参数 i 油时取值 1，水时取值 2；m：孔隙率；Si：第 i 相的饱和度真密度；k0：绝对相渗透率；fi：相对相渗透率；μi：动态粘度；ρU=（ρ1с1+ρ2с2）是混合物的比内能热传导（λ）引起的热通量矢量。式（1-3）中，未知量为速度压力（P），温度（T），和饱和度（S）i。对于方程组（1-3），参数在 τ=0 时的初始分布设置流动区域以及该区域边界上的条件。

2 问题描述

本文考察了“注入井-储层-生产井”系统，水平注入和生产井系统在油田作业期间发生的准三维等温非平稳过程。涉及上述系统相关问题的假设见图1。

图1 中，H：储层厚度；LZ：井的水平段的长度；ΔZ：沿 Z 轴的模型细胞的尺寸；W：水；O+W：水-油混合物。

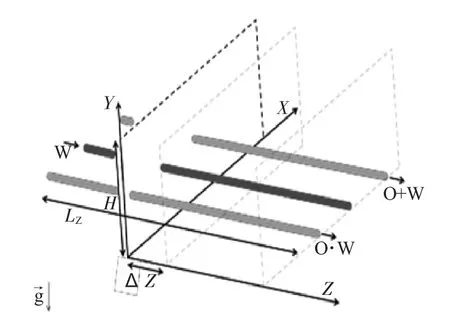
图1 平行水平井系统准三维问题示意图Fig.1 Schematic diagram of quasi three dimensional problems of parallel horizontal well system

三维问题简化为3 个相互关联的组合：（1）在注入井水平段中改变压力，水（蒸汽）流量和温度（在解决热问题的情况下）的准一维问题；（2）Nx二维两相在垂直层渗透问题ΔZi=LZ/NZ；（3）油水的压力，温度和流量变化的准一维问题。在井的水平部分注水（在此阶段，我们只能解决两相渗流问题）。油水混合物沿Z 轴在生产井的水平段中流动0≤Z≤LZ；热水或其他冷却剂沿Z 轴流动；而Z 从Z 取值范围[0, LZ]，假设渗透率沿Z 轴的投影（Wz）比Wx 和Wy 小得多，因此，式（4）成立。

考虑时间为参数已知分布的准平稳近似：tn和随时间Δt 的某些外部影响，时间tn+1=tn+Δt，其中n=1，N。在实践中使用的开发系统（图1）通过解决以下3 个问题来描述：注入井水平段系统-地层-生产井水平段系统中传热和传质的三维非平稳问题。旨在改进用于计算流体力学参数的方法，假定已知渗流区域内的温度场。

3 模型设计

在第2 节的假设基础上，在储层区域和井横截面中形成计算网格。提出了解决问题的迭代方法。

3.1 模型数据设置

几何尺寸：注射井直径（di）和生产井直径（dp）；井水平段之间的距离（Lx）；井水平段有效长度(LZ)；

初始油藏参数分布 孔隙度（m）、绝对相渗透率（Ko）和相对相渗透率（fo, w（Sw））、水或油饱和度（So=1-Sw）、初始时刻油藏的压力（P0）和温度（t0）；

注入井（Pi）和生产井（Pp）初始压力，注入井的初始温度（Ti）和速率（Go, w）；

计算参数 时间步长（Δt），断面数（Nz），流线和等势面数，流量迭代时的误差（ξG）。

3.2 模型计算

注产井水平段沿长度0≤x≤Pi, p（x,t）和温度Ti（x,t）的初始分布；压力分布由动量平衡方程表示，可用式（5）表达：

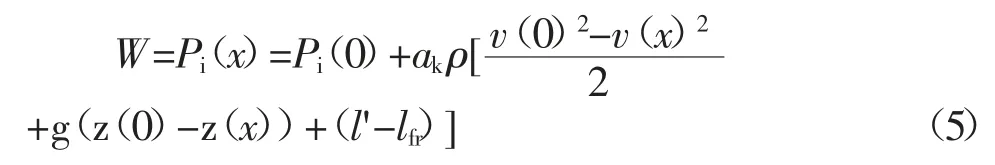
确定流线的初始位置：等势面在平面上Zi=const为定义常量，控制量形成于线的交点。因此，使用自然坐标系其中，考虑到研究对象的几何形状（图1）和边界影响，以源和汇的叠加形式呈现，li对应等势线φi和流线ψj计算过程中确定，式（6）：

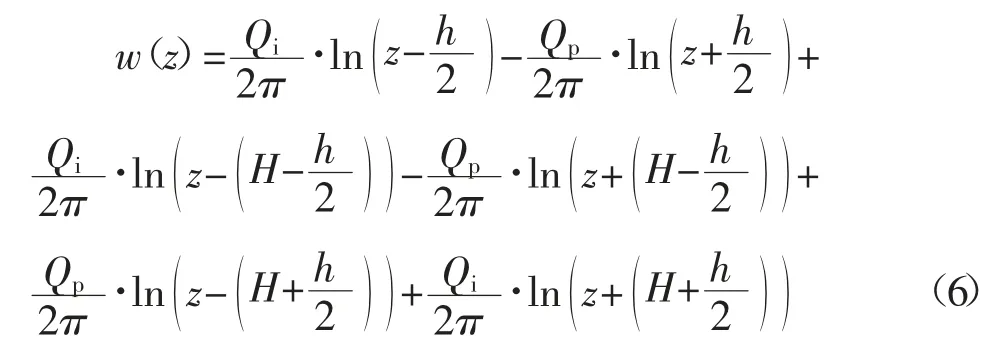
从水平井中的准一维流体运动方程组中沿长度0≤x≤L 的速度、压力、饱和度、温度的变化。沿气流的压力分布可表示为式（7）：

从式（7）中可以确定混合物气流流速l'=Lj，其中Lj是当前流长度。令可得式（8）：

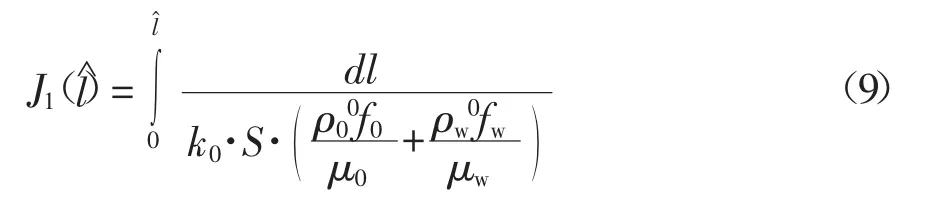
在考虑到（8）和（9）的情况下，沿水流的相速度分布 l 如式（10），式（11）：

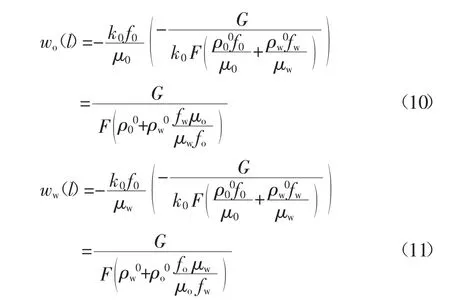
油水流量在 l=L 与区域 F（L）部分时，如式（12）方程组所示：

在时间tn+1时第i 相的饱和度等于：

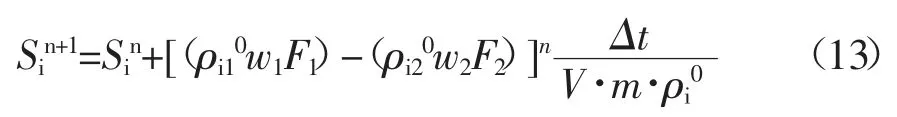
在自然坐标系中，利用式（6）中找到的控制量，通过类比考虑流线的形状，可确定水流和相流的初始压力分布。采用动态自然半固定坐标系来划分空间。渗透流量参数的不断变化，对流线进行细化。按照上述步骤反复进行，直到获得式（14）收敛条件。

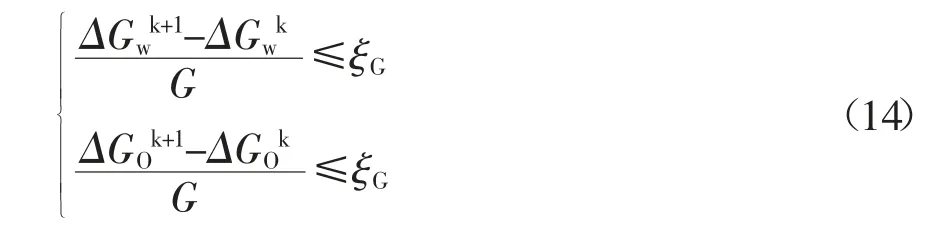
其中k 为迭代次数，ξG为迭代过程中对各层流的允许误差根据上述步骤重复计算时间间隔其中 Nt为时间步数。

4 案例分析与数值模拟

使用某地区的真实数据以进行仿真分析，根据数字随机孔网络建模的结果设置了相对相渗透率函数，表1 汇总了用于计算的初始数据。

表1 初始数据设定Tab.1 Initial data setting

第一阶段，计算出各种模式的田间开发技术指标。

不同压力条件下，产油产水量随时间变化见图2。在不同ΔP 条件下，产油产水量都呈上升趋势。在ΔP=80atm 时，累计产油量最高。

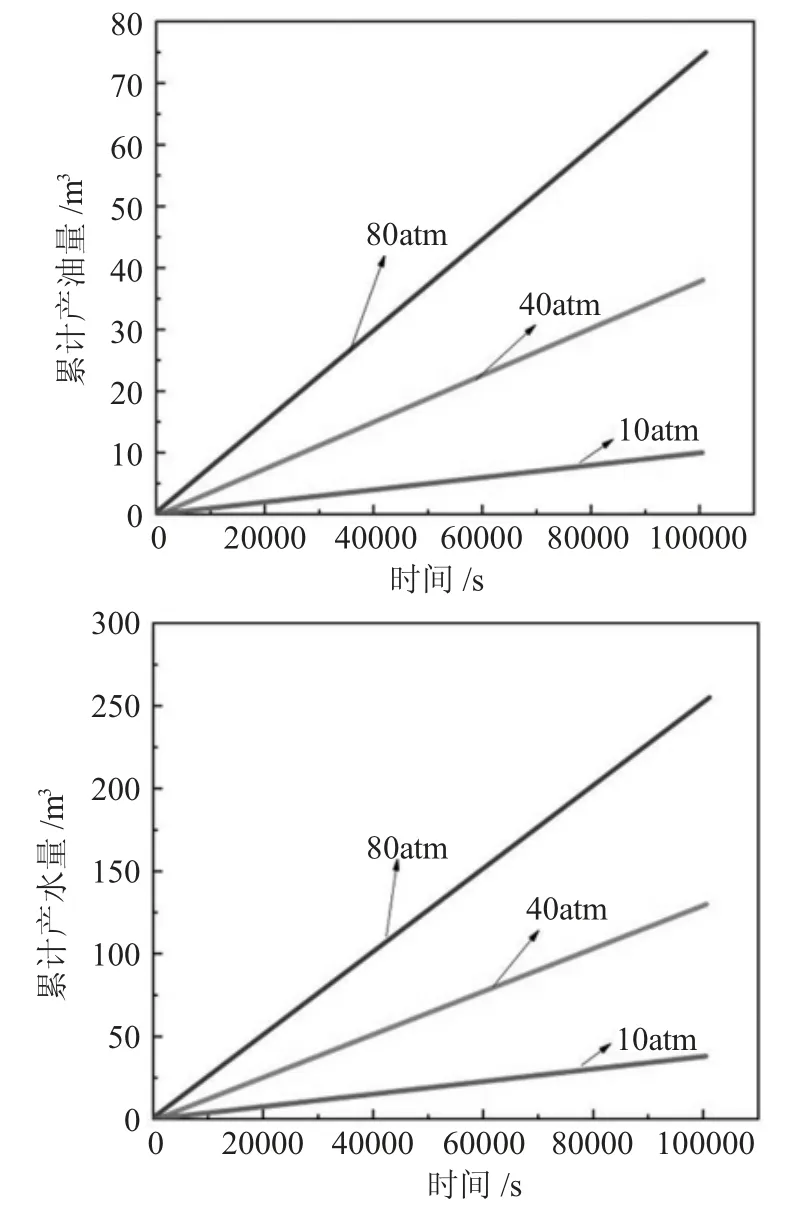
图2 不同压力条件下产油产水量时间变化Fig.2 Time variation of oil and water production under different pressure conditions

用不同的初始地层温度进行了一系列等温计算（图3）。初始地层温度为20、60 和80℃，在这一系列实验中，影响结果的关键因素是流体粘度，表面张力和相对渗透率图的变化的依赖性[11,12]。从储层流体样品中获得了动态粘度和表面张力的依赖关系，并通过模型证明了相对渗透率图中的变化规律。

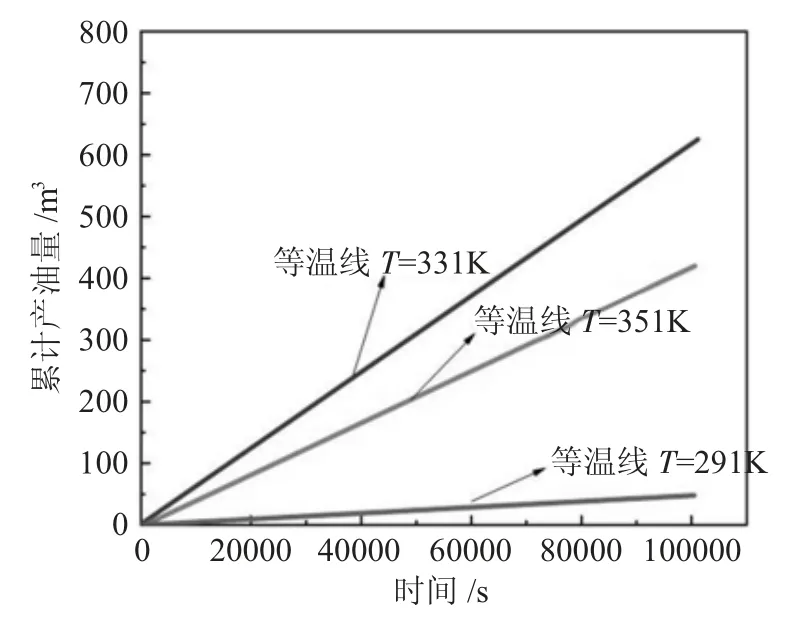
图3 不同初始温度等温曲线Fig.3 Isothermal curves of different initial temperatures

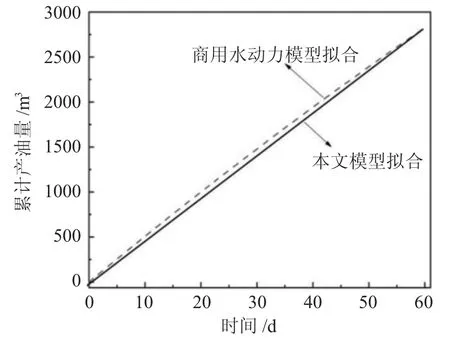
图4 本文模型与商用模型结果比较Fig.4 Comparison of the results of the model and commercial model

应用多相系统主题力学的基本规律，结合现代物理、数学模型和数值方法进行求解，提供了研究的可靠性。用商业水动力模型对数据进行验证，证实了所获得的结果（图4）。

5 结语

基于自然半固定坐标系中动态计算网格的构建，开发了一种用于稀疏化确定渗流两相混合物，并将其实现为可编程模型，平行水平井系统准三维非平稳等温运行模型。以某高粘度油田为例，利用平行水平井系统对各种开发模式进行了计算参数研究。所提出的计算方法及其软件实现是对传热和传质过程进行进一步建模的基础，为从本领域理论研究和数值模拟提供借鉴。