不同温度环境下加肋土工膜与砂土界面拉拔试验的颗粒流数值模拟

高俊丽，徐宏飞，袁 川，曹 威

(上海大学土木工程系，上海 200444)

垃圾填埋场中部分垃圾在降解发酵过程中会产生大量热量，导致衬垫系统内部温度升高，影响了衬垫系统中土工合成材料的力学性质，在一定程度上影响了填埋场的安全稳定性. 已有很多专家对土工材料的温度效应进行了研究. Bely 等[1]发现温度的变化通常导致界面摩擦系数的变化. Osswald等[2]发现温度的升高通常会导致土工材料松弛时间的减少. Irsyam等[3]通过直剪试验，并且利用热蜡对土工格栅的剪切面进行了研究，提出了横肋端承阻力的计算公式. 许四法等[4]对温度和填埋高度引起的垃圾填埋场边坡土工膜张拉力进行了分析. 结果表明: 当填埋高度较小时，作用在HDPE 土工膜端部的张拉力主要为温度应力; 温差越大，土工膜端部的张拉力越大; 随着填埋高度的增加，填埋引起的HDPE 土工膜端部张拉力增大. 景苏明[5]对土工格栅拉拔试验界面等效摩擦力进行了研究，针对土与土工格栅组成的加筋土，分析了拉拔试验过程中加肋土工膜与砂土界面产生的等效摩擦力及各自所占的比重. 高俊丽等[6-7]探讨了加肋土工膜与砂土界面的相互作用机制，给出了加肋土工膜与砂土界面总阻力由面摩阻力、肋块所受端承阻力和侧摩阻力3 部分组成的具体表达式，并通过大量直剪试验研究了在不同正应力和加肋间距下土工膜与砂土之间的界面特性和强度特性.

还有学者采用有限元方法和离散单元法，将宏观试验与数值模拟相结合，对加肋土工膜与砂土界面的作用机制进行了更深入的探讨. 张孟喜等[8]采用二维颗粒流程序(2D particle flow code，PFC2D)对H-V 加筋土进行了模拟，很好地拟合了立体加筋砂土三轴试验的应力-应变曲线，并通过研究颗粒的受力情况分析了H-V 加筋砂土的受力原理. 本工作基于离散单元法的二维颗粒流程序(PFC2D)，从细观角度对加肋土工膜与砂土界面拉拔试验进行了数值模拟，将宏观力学性质与其细观变化联系起来，分析了不同工况下土工膜的拉拔应力-位移图、颗粒位移矢量分布图和模型内部接触力分布图，对加肋土工膜与砂土界面的作用机理进行了更深入的研究.

1 颗粒流数值模拟

若在模拟中采用与砂土颗粒相同半径的Ball 单元，会使生成的颗粒过多. 周健等[9]研究了颗粒数目对双轴试验结果的影响，认为当颗粒数量超过2 000 个时，对试验结果影响不大，因此在不改变砂土级配、不均匀系数和曲率系数的前提下，可适当提高颗粒半径. 同时砂土与土工膜的颗粒级配参考了郑俊杰等[10]的颗粒粒径参数，设置最小粒径为1 mm，最大粒径为3.8 mm，对模拟结果不产生实质的影响. 图1 为试验用砂与PFC 模型颗粒级配的对比图.

图1 试验用砂及PFC 模型颗粒级配对比Fig.1 Comparisons of the grain size gradation between the test sand and the PFC model particle

1.1 建立模型

在建立PFC2D颗粒流拉拔模型时，采用Wall 单元模拟拉拔试验箱，生成宽为300 mm，高为300 mm 的矩形区域. 采用Ball 单元来模拟砂土颗粒和土工膜: 首先在矩形区域内随机生成相应的颗粒; 然后通过Fish 语言将指定范围内的土颗粒删除; 最后生成加肋土工膜模型，这样可避免颗粒重叠的问题. 加肋土工膜模型如图2 所示. 本研究模拟了不同温度(7，16，25°C)和不同加肋高度(0，3，4.5，6 mm)组合的室内拉拔试验. 由于温度对土工合成材料的表面摩擦性质有很大的影响，所以本研究通过改变加肋土工膜与砂土界面的摩擦系数来模拟温度情况，并且通过改变土工膜肋块颗粒层数(2 层为3 mm，3 层为4.5 mm，4 层为6 mm)来模拟加肋高度变化. 完整的PFC2D颗粒流模型如图3 所示.

图2 加肋土工膜模型Fig.2 Model of the ribbed geomembrane

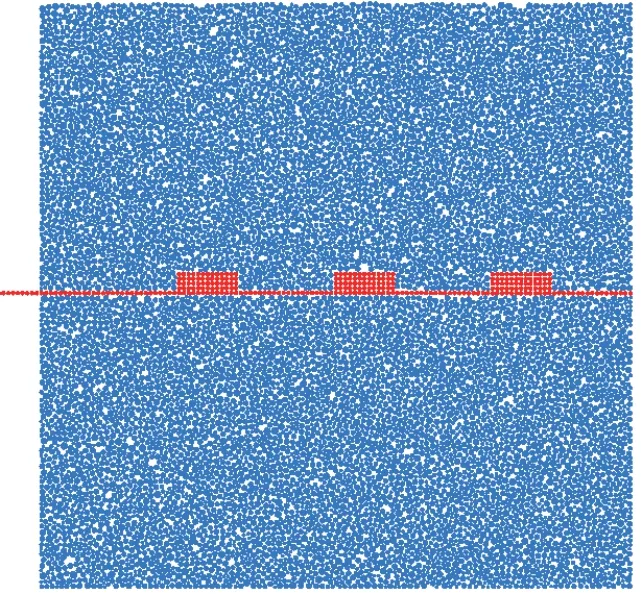
图3 PFC2D颗粒流模型Fig.3 Mode of PFC2D

1.2 细观参数标定

由于颗粒流模拟很难找到细观参数与宏观参数之间的对应关系，那么能否达到与试验结果相同的宏观特性是判别颗粒流模拟是否合理的重要依据. 本研究的细观参数是根据光面土工膜的基本物理性质(弹性模量、密度和伸长率等)和室内拉拔试验结果所表现出的宏观力学参数(极限拉拔应力、泊松比等)来确定的，具体模型参数如表1 所示.

表1 细观参数Table 1 Mesoscopic parameters

为了验证PFC 数值模型所选用参数的合理性，在温度为7°C，肋块高度分别为3，4.5 和6 mm 的条件下进行观测模拟，绘制出拉拔应力τ(kPa)与拉拔位移u(mm)的关系曲线，并与室内试验数据进行对比，结果如图4 和表2 所示. 可知，PFC2D模拟所得的拉拔应力-位移曲线与试验结果具有相同的变化规律和发展趋势，在数值上也基本满足分析的要求，误差不超过10%. 在不同温度情况下，极限拉拔应力的试验值与模拟值的比较结果如表3 所示. 可见，误差率也不超过10%. 综上，可以认为本研究选取的参数是合理的，能够准确模拟拉拔模型试验情况. 因此，可以采用该模拟模型对试验内部情况进行深入分析.

表2 不同高度下极限拉拔应力数值模拟与试验数据对比Table 2 Comparisons of the ultimate tensile stress between the numerical simulation data and the test data under different heights

表3 不同温度下极限拉拔应力数值模拟与试验数据对比Table 3 Comparisons of the ultimate tensile stress between the numerical simulation data and the test data under different temperatures

图4 数值模拟与室内拉拔试验的拉拔应力-位移对比Fig.4 Comparisons of the drawing stress-displacement between the numerical simulation data and the test data

2 颗粒流模拟结果与分析

2.1 高度对拉拔应力-位移关系曲线的影响

当温度为7°C 时，由图5 可知，随着加肋高度的增加，极限拉拔应力也随之增大. 相比光面土工膜(h= 0 mm)，加肋土工膜的极限拉拔应力明显更大: 加肋土工膜(h= 3 mm)的极限拉拔应力相比光面土工膜(h= 0 mm)提高了101.3%; 加肋土工膜(h= 6 mm)的极限拉拔应力(h=3 mm)相比加肋土工膜又提高了54.3%. 这说明随着加肋高度的增加，模型的抗拉拔强度更高.

图5 不同高度下的拉拔应力-位移图Fig.5 Diagram of the drawing stress-displacement under different heights

2.2 温度对拉拔应力-位移关系曲线的影响

通过对不同温度(7，16，25°C)拉拔试验模拟发现，温度对拉拔应力有着较为明显的影响.由图6 可知: 在开始阶段，加肋土工膜(h= 6 mm)和光面土工膜(h= 0 mm)的拉拔应力都随着位移的增加快速发展，当达到一定值时，随着位移的增加有一定的上下波动，然后趋于稳定;通过PFC 模拟的拉拔模型结果发现，随着温度的降低，极限拉拔应力显著增加，结构稳定性更强. 结合表4 可以得出，随着加肋土工膜与砂土界面摩擦系数的增大，拉拔应力也逐渐增加.这与周健等[9]用颗粒流程序模拟砂土双轴试验时，得到的“随着界面摩擦系数的增大，峰值应力也有所提高”的规律一致.

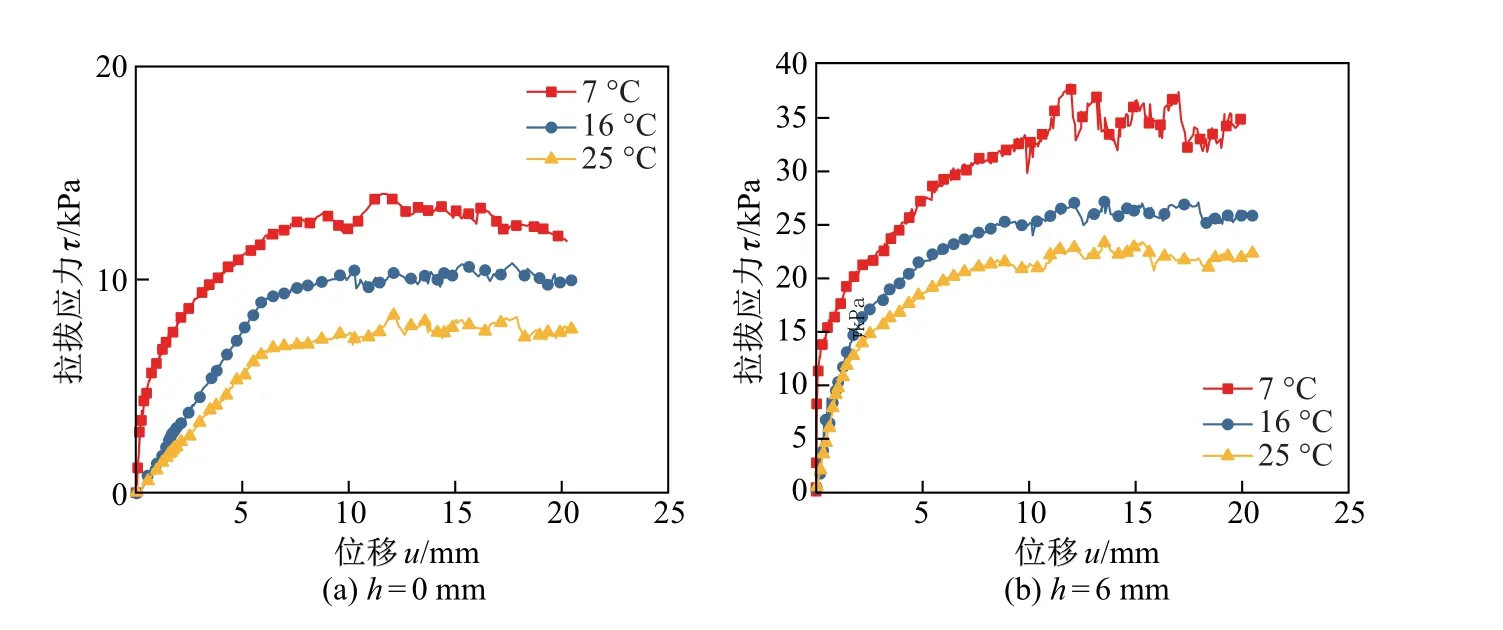
图6 不同温度下的拉拔应力-位移图Fig.6 Diagram of the drawing stress-displacement under different temperatures

2.3 加肋土工膜与砂土界面的摩擦系数分析

由表4 可知，在拟合了宏观的拉拔应力-位移曲线的情况下，加肋土工膜与砂土界面摩擦系数的模拟值明显高于试验值. 这是由于模拟中的填土和筋材所用颗粒都设置成圆盘状，而实际试验中的填土为不规则砂土. 不规则性使得砂土与加肋土工膜之间的摩擦力要比圆形颗粒大很多. 因此在PFC 模拟时，需要通过增大界面摩擦系数来减小颗粒形状的影响. 从表4 还可以看出，在25 kPa 下，在7～16°C 阶段，加肋土工膜与砂土界面的摩擦系数下降了0.26; 而在16～25°C 阶段，界面摩擦系数下降了0.22. 由此可知，随着温度的升高，颗粒流数值模拟的界面摩擦系数也是逐渐下降的.

表4 不同温度下界面摩擦系数数值模拟与试验数据对比Table 4 Comparisons of the interface friction coefficients between the numerical simulation data and the test data under different temperatures

2.4 位移场分析

图7 为加肋土工膜(h=6 mm)被拉出20 mm 后的位移分布图，其中颜色代表位移大小(位移从大→小，颜色从红→紫)，箭头代表方向. 为了更清晰地分析土颗粒的运动趋势. 将图7 分为A，B，C 3 个部分进行分析，结果如图8 所示. 由图8(a)可知，在拉拔过程中，肋块附近的土颗粒往拉拔方向有明显的位移和旋转. 由于左侧墙体限制了模型中土颗粒的移动，所以在拉拔过程中土颗粒由向左运动转而向上运动. 由图8(b)可知，位于肋块中间的区域，土颗粒有向上、向左的运动趋势. 这与林永亮等[11]利用土工格栅进行拉拔试验的数值模拟结果大致相同. 由图8(c)可知，靠近最右侧肋块附近区域，由于土颗粒向左运动，此区域土颗粒产生松动现象，肋块后部上方的土颗粒在法向应力的作用下有向下的运动趋势.

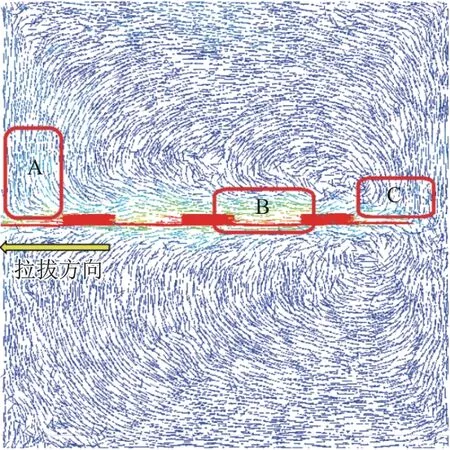
图7 拉拔过程中的颗粒位移矢量分布图Fig.7 Vector distributions of the particle displacement during the drawing

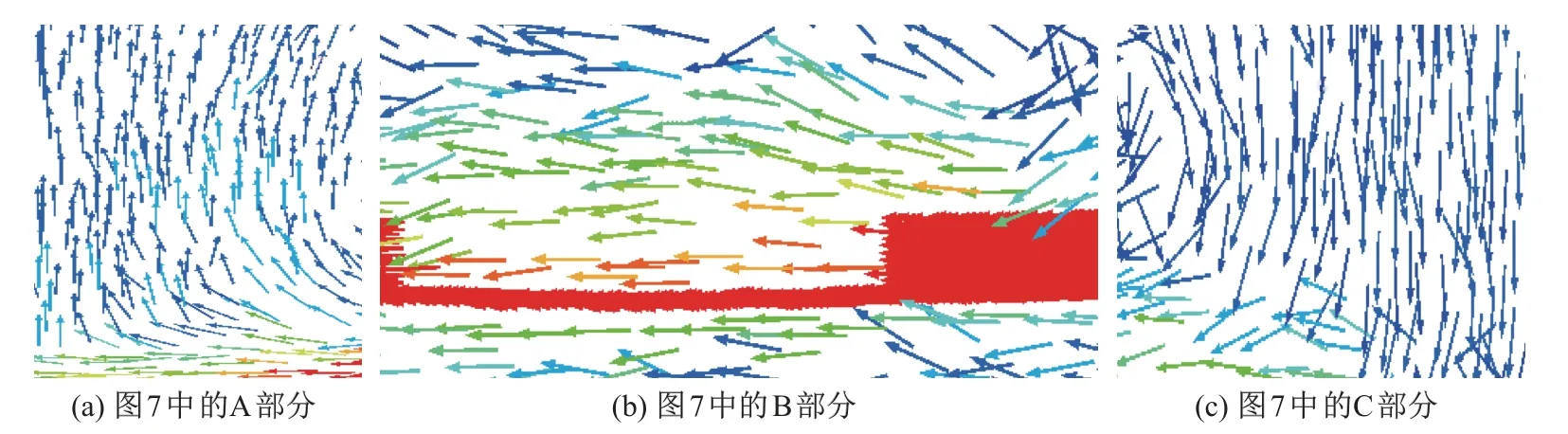
图8 拉拔过程中的土颗粒运动趋势图Fig.8 Motion trend of the soil particles during the drawing

图9 是在不同温度下，加肋土工膜(h=6 mm)被拉出20 mm 后的加肋土工膜与砂土界面附近颗粒位移图. 可知，随着温度的升高，加肋土工膜与砂土界面附近的砂土颗粒位移逐渐变大，结构稳定性变弱. 这是因为在相同的拉拔速率和位移情况下，加肋土工膜与砂土界面附近的砂土颗粒位移越大，说明土体抵抗拉拔应力的能力较差，整体的稳定性较差.

图10 是在温度为7°C 时，不同加肋高度的加肋土工膜被拉出20 mm 后的加肋土工膜与砂土界面附近颗粒位移图. 可知: 光面土工膜(h= 0 mm)与砂土界面附近的砂土颗粒运动方向主要为向下运动且位移较小，受到拉拔的影响较小，整体抵抗拉拔应力的能力较差; 随着加肋高度的增加，加肋土工膜与砂土界面附近的砂土颗粒位移减小，整体稳定性变强. 这说明加肋土工膜的稳定性明显优于光面土工膜.

图10 不同高度下颗粒位移矢量分布图Fig.10 Vector distributions of the particle displacement under different heights

2.5 加肋土工膜拉拔模型中颗粒间接触力分布

图11 为加肋土工膜(h=3，6 mm)被拉出20 mm 后的接触力(颗粒所受到的合力)分布图，其中黑色线条代表接触力，线条的粗细代表接触力的大小. 对比图11(a)和(b)可知，随着加肋高度的减小，加肋土工膜与砂土界面附近砂土颗粒的接触力明显减小. 这说明加肋的效果明显减弱，土体内部的相互作用变弱，整体稳定性变差.

由于每种工况的内部接触力分布规律类似，因此以加肋高度为6 mm 的情况为例来分析内部接触力分布情况. 从图11(b)中可以看出: 由于左侧墙体限制了模型中土颗粒的移动，所以在拉拔过程中，第一根加肋处接触力最大，第二根与第三根逐渐减少，与林永亮等[11]所述的接触力分布规律类似; 而且在第一根肋块处接触力最大，并以加肋土工膜为中心向上、下两边逐渐减小，与Dyer[12]采用光弹法观察加筋格栅承载杆件周围应力的分布规律类似. 同时由图12 可知，肋块在模型拉拔过程中挤压其左侧的颗粒或带动颗粒一起移动，使得接触力较大而形成高应力区，而在肋块另一侧，由于土体松动，接触力明显变小，出现低应力区.

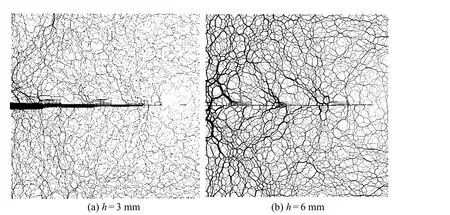
图11 接触力分布Fig.11 Contact force distributions

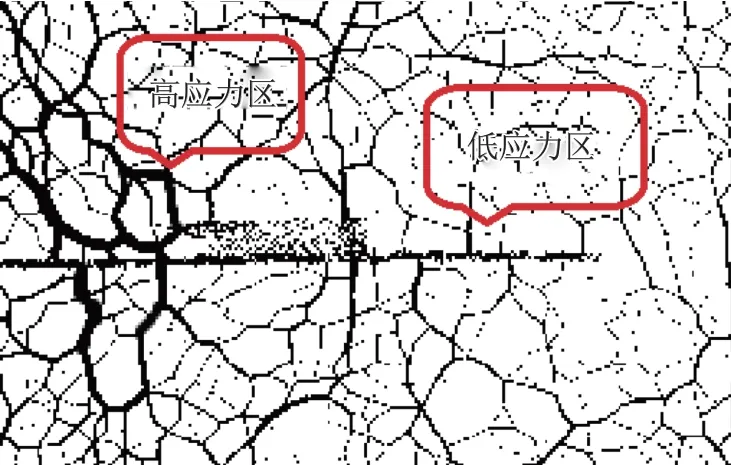
图12 肋块附近应力分布Fig.12 Stress distributions near the rib

2.6 小 结

颗粒流模拟从拉拔应力-位移关系曲线与细观角度(界面附近颗粒的位移与接触力规律)，探究了加肋高度和温度对极限拉拔应力的影响; 通过比较各种工况，得出了最优试验加肋高度和温度，并给出了相应的关系——加肋土工膜与砂土界面稳定性随着加肋高度的增加和温度的降低有明显的提升. 这是因为筋土间的相互作用力包含光面土工膜的面摩擦阻力、肋块端阻力和肋块侧摩擦力[6]. 随着肋块高度增加，肋块端阻力明显增大，此时筋土间的相互作用力主要由肋块端阻力决定. 温度对土工合成材料的强度、变形有较大影响: 温度越高，其强度越低，变形越大; 温度越低，其强度越高，变形越小，说明低温情况下土工膜的物理性质更稳定.这对实际垃圾填埋场底部温度的把控具有很有效的指示作用，并且进一步证明了加肋土工膜相对于光面土工膜的优势，即更容易提高填埋场底部的承载强度且制作简单、经济.

3 结束语

本研究基于室内拉拔试验，运用颗粒流细观数值模拟研究了拉拔试验的细观颗粒变化情况，分析了PFC2D数值模拟的合理性，揭示了加肋土工膜拉拔试验中加肋土工膜与砂土界面的相互作用机理，从宏观到细观分析得出如下结论.

(1) 采用PFC2D软件可较好地从细观角度对加肋土工膜与砂土界面的特性进行揭示，并与拉拔试验结果进行了对比与分析，验证了其合理性与可行性.

(2) 在相同法向应力和相同温度作用下，加肋土工膜的作用效果明显高于光面土工膜. 在相同法向应力和相同加肋高度作用下，随着温度的升高，极限拉拔应力逐渐降低，并且加肋土工膜与砂土界面的摩擦系数也逐渐下降. 这说明界面摩擦系数对温度有很强的依赖性，低温下界面摩擦系数越高，拉拔应力越大，模型的稳定性越强.

(3) 通过对颗粒位移的观测，拉拔过程中肋块向左移动对附近的土颗粒位移有较大影响，肋块左边土颗粒向左上方移动，而右边土颗粒有向左、向下运动的趋势. 随着温度的降低或者肋块高度的增加，加肋土工膜与砂土界面附近砂土颗粒的位移变小，整体的稳定性变强.

(4) 在拉拔过程中，接触力从加肋土工膜界面向上、下两边逐渐减小，肋块左侧的接触力大于肋块右侧，处于高应力区. 第3 个肋块后方接触力最小，处于低应力区. 随着加肋高度的增加或者温度的降低，加肋土工膜与砂土界面附近砂土颗粒的接触力明显增大，整体的稳定性变强.