不同飞行高度下超声速来流/射流及其相互作用的数值模拟
2021-02-26放韩桂来刘美宽丁珏翁培奋姜宗林
邓 放韩桂来刘美宽丁 珏翁培奋姜宗林
(1.上海大学上海市应用数学和力学研究所,上海 200072;2. 中国科学院力学研究所高温气体动力学国家重点实验室,北京 100190;3. 中国科学院大学工程科学学院,北京 100049)
后台阶流动、射流一直是流体力学关注的重要的基本流动现象[1-4],而后台阶流动和射流的组合流动也普遍存在于流体力学的各个领域. 在火箭发射和飞行过程中,火箭处于不同的飞行高度,由于环境空气密度随着高度的增加而变小,火箭周围的气体静压也随着高度的增加而变小,发动机尾喷管产生的射流形态也发生变化: 由地面附近的过膨胀形态转变为高空时的欠膨胀形态[5-8]. 火箭喷管附近流场存在着复杂的超声速来流和燃料射流相互作用情况,可通过两步后台阶模型模拟超声速来流与射流相互作用进行研究. 二者相互作用产生的回流区,会对射流形态产生影响,并影响到火箭发动机喷管的防热[9-11]. 气动喷嘴产生的燃料气体与喷嘴周围的空气掺混[12]、超燃冲压发动机中支板产生燃料射流和发动机内流相互作用[13]等现象也可视为两步后台阶处超声速来流和射流相互作用的流动现象. 因此超声速来流与射流在两步后台阶处相互作用的现象具有重要的科研价值和工程意义.
已有的工作主要运用后台阶研究流动产生流体分离和再附、后台阶回流区内涡结构等现象[14-16]: 超声速来流在台阶拐角处由于外形的突变,产生流动分离现象; 气体快速膨胀并在台阶下游位置产生一个剪切层,剪切层和后台阶下壁面之间形成回流区; 回流区内存在着复杂的涡结构. Biswas等[17]研究了膨胀比H/h= 1.942 3,2.5 和3.0 的后台阶流动,以及在流动方向上来流的空间演化和三维效应. 结果发现,在靠近内侧壁处的剪切层存在向回流区喷射的现象. Hasan等[18]通过实验研究了Re= 11 000 时层流分离的后台阶流动. 结果表明,与未受扰动的流动相比,扰动增加了剪切层的生长速率和湍流强度,并减少了再附长度. 扰动频率及其谐波幅度的测量结果也表明,剪切层存在失稳. Reddeppa等[19]在高超声速激波风洞中研究了Ma=7.6 时的后台阶流动. 结果发现,后台阶表面传热率会受到台阶高度的影响.
射流普遍存在于燃烧反应过程、发动机喷流等研究领域. Zapryagaev等[20]通过实验确定,从轴对称喷嘴排出的超声速射流剪切层的初始部分具有三维结构,欠膨胀射流初始段是由膨胀扇、剪切层、拦截激波等基本结构构成的. Imamoglu等[21]运用大涡模拟和加权本质无振荡(weighted essentially non-oscillatory,WENO)格式求解Navier-Stokes 方程组,发现模拟射流激波胞格结构良好地符合实验结果. 刘昕等[22]研究了不同射流与环境静压比下,欠膨胀超声速射流近场的流场结构. 结果发现,在欠膨胀超声速射流情况下,欠膨胀射流方向出现的拟周期性拦截激波是欠膨胀射流稳定发展的特征,而这种拟周期性欠膨胀激波结构的消失是射流失稳开始的标志.
本工作分别研究了不同飞行高度下超声速后台阶流动、射流以及超声速来流/射流相互作用的流场结构和流动规律. 采用高精度格式离散Navier-Stokes 方程,通过改变不同来流条件参数,重点对流场的回流区涡结构、射流膨胀扇、两个剪切层的相互作用等展开研究和讨论.
1 物理模型和数值方法
1.1 物理模型
本工作采用两步后台阶作为基本模型,研究了超声速后台阶流动、射流和超声速来流/射流组合流动这3 种流动形式. 超声速后台阶流动的物理模型如图1(a)所示: 从边界AB 处产生Ma= 3 的超声速来流,来流经过点C 时发生分离,产生来流剪切层. 射流的物理模型如图1(b)所示: EF 处喷出Ma= 2 的高温高压射流,射流边界附近形成射流剪切层. 超声速来流/射流组合流动的物理模型如图1(c)所示: 边界AB 处产生Ma= 3 的超声速来流,气流从点C 处膨胀分离,形成一个来流剪切层; EF 处产生Ma=2 的射流. 因为射流出口处的静压显著高于环境静压,因此此时射流的类型为欠膨胀射流,在射流边界附近会出现射流剪切层. 来流剪切层和射流剪切层在第二个台阶上方相互作用,形成复杂的流场结构. 考虑到流场的对称性,本工作流场的计算区域、CUP 和网格分布如图2 所示,其中CUP 总数为72,网格总数为180 万,采用矩形结构网格. 由于网格太密,图2(c)为稀疏后(总数为1.8 万)的网格分布. 壁面BC,CD,DE 为绝热壁,HG 采用外推的无穷远边界条件,AH 采用超声速无反射边界条件,FG 采用对称边界条件,AB,EF 相应的边界条件如表1 所示.

表1 边界条件Table 1 Boundary conditions
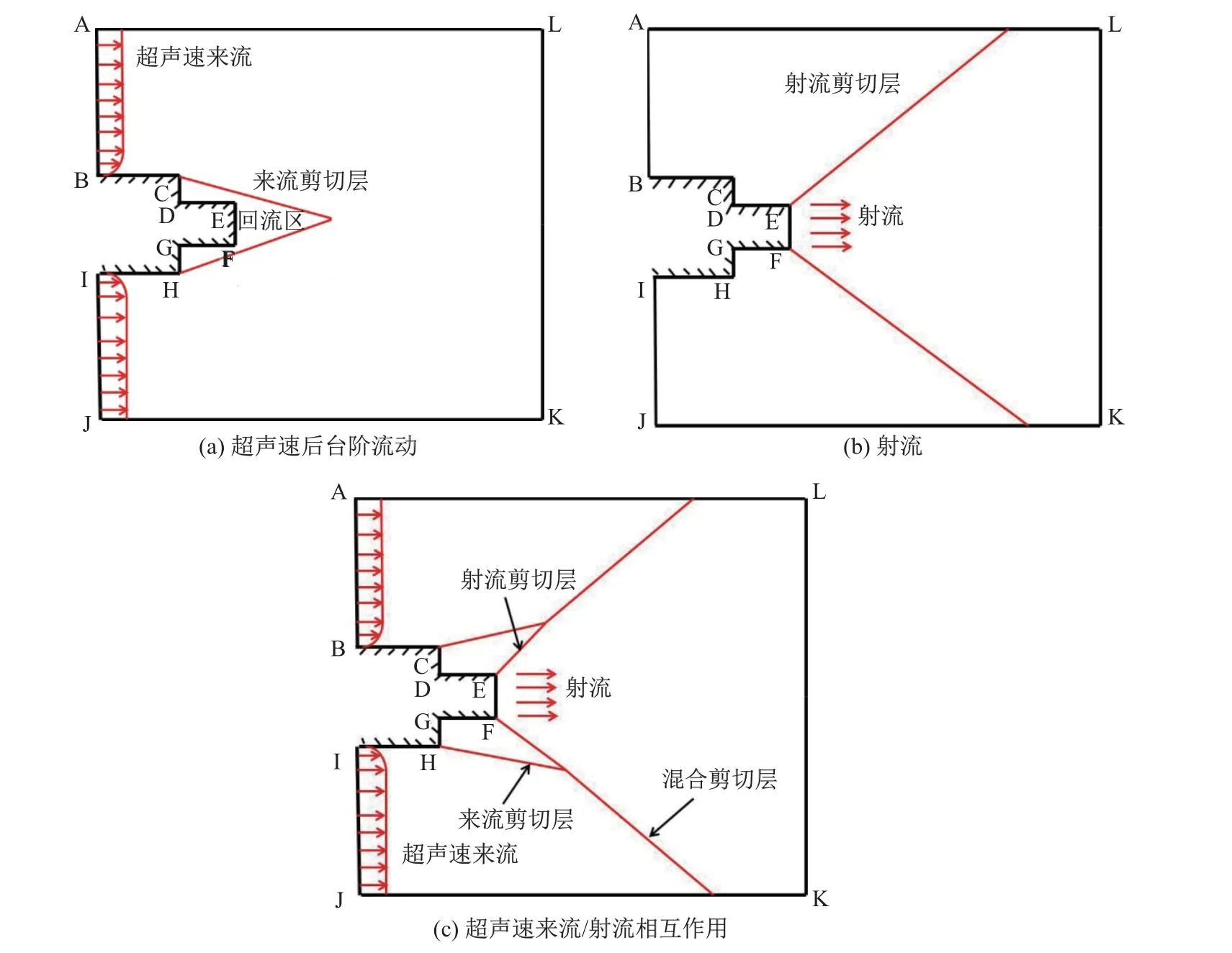
图1 物理模型Fig.1 Physical models

图2 计算域、CUP 和网格分布Fig.2 Computational domain,CPU and grid distributions
当超声速来流的Ma= 3 时,选取了3 种不同飞行高度的国际标准大气(international standard atmosphere,ISA)条件作为来流的参数条件,选取的高度分别是20,30 和50 km,具体参数如表2 所示. 后台阶EF 处射流的Ma=2,参数设置如表3 所示,组分也为空气.

表2 20~50 km 飞行高度的高空大气标准参数Table 2 Atmospheric standard parameters at 20~50 km flight altitudes

表3 射流参数Table 3 Jet flow parameters
1.2 控制方程
在笛卡尔坐标系下,二维无量纲化Navier-Stokes 方程表示为

式中: 下标v表示粘性项; 各矢量形式为

式(2)~(6)中的ρ和p分别表示气体的密度和压力;u,v分别表示x,y方向上的速度分量; 各黏性应力分量为

各方向上的热流分量为

其中黏性系数μ根据Sutherland 公式确定,Pr=0.72.
控制方程需要通过变换关系实现物理空间(x,y)向计算空间(ξ,η)的变换. 直角坐标系下的控制方程经过Jacobian 变换之后,计算空间中的Navier-Stokes 方程表示为

式中: 各矢量形式为

Jacobian 行列式为

取参考量L为特征长度,u0=a0,即来流速度为特征速度,温度T0、分子黏性系数μ0、密度ρ0为特征变量. 对应的特征时间t0=L/u0,特征压强,各无量纲量分别为
1.3 计算方法
本工作分别应用五阶精度WENO 格式[24]、六阶精度中心差分格式离散对流项和粘性项[25],时间推进应用三阶精度Runge-Kutta 格式[26]. 采用MPI 非阻塞并行模式,网格总数180 万,使用72CPU 在广州天河二号上运行.
Steger-Warming 流通量矢量分裂法通过对特征值进行分裂,表示为

五阶精度WENO 格式对流项离散形式[24]如下:
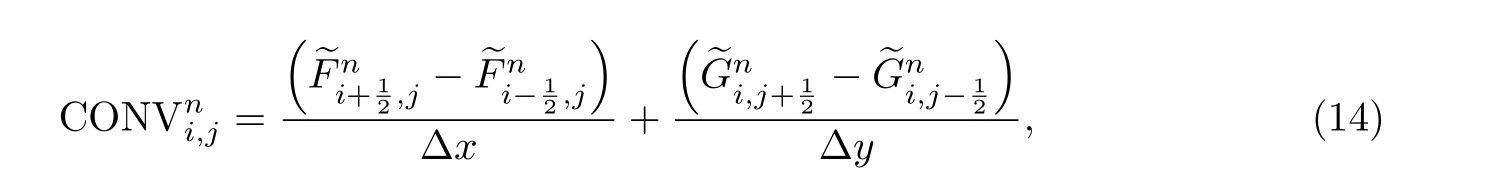
式中,CONV 表示对流项.
矢通量构造为
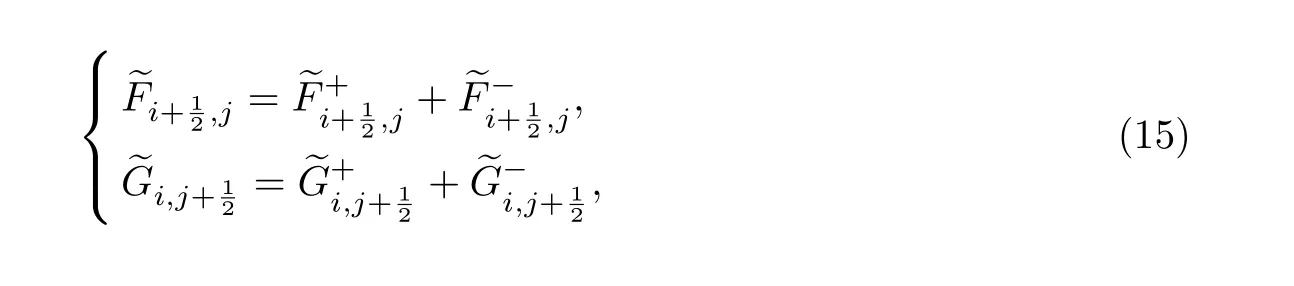
式中:

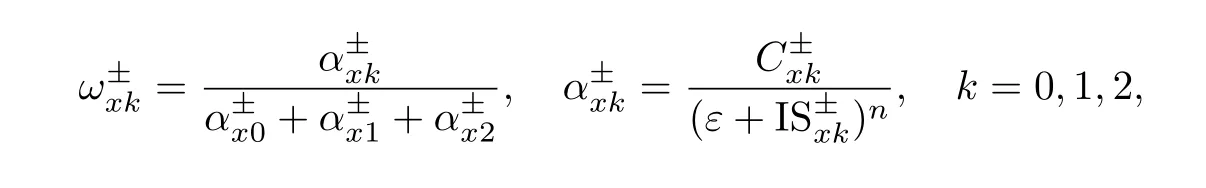
其中IS 为光滑度量函数;n为一个整数. 本工作根据Jiang等[24]的建议,取n=2.
组合系数如下:

G通量的构造方式类似,替换F为G即可获得表达式.
粘性项半离散逼近式[25]如下:
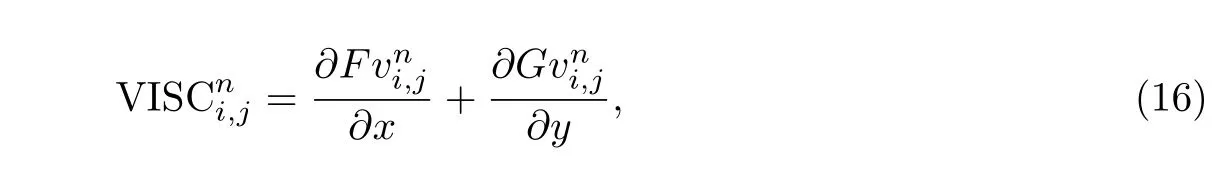
式中,六阶精度中心差分格式导数项可以离散表示为
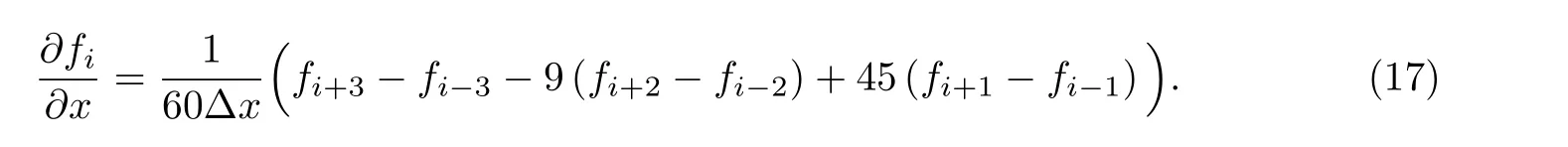
时间积分采用三阶精度Runge-Kutta 方法[26],即
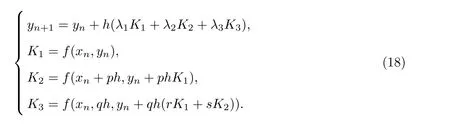
1.4 数值验证和网格无关化验证
使用平板超声速流动的算例来验证计算方法的正确性和可靠性. 超声速来流的Ma= 7,雷诺数Re=1.233×106. 如图3 所示,在前缘激波之后,超声速来流密度变小,并且边界层沿着超声速来流方向逐渐变厚. 这与平板超声速流动的实验情况一致.

图3 平板上超声速流动密度分布图Fig.3 Density distributions of the supersonic flow on a plate
采用可压缩边界层的自相似解用于数值比较. 可压缩边界层的自相似解是半解析解. 本工作采用五阶Runge-Kutta 方法结合打靶法求解自相似解. 将半解析解与数值模拟解进行比较,来验证数值模拟的代码和代数方法. 如图4 所示,数值模拟曲线与半解析解曲线吻合良好,表明该算法是可靠的.
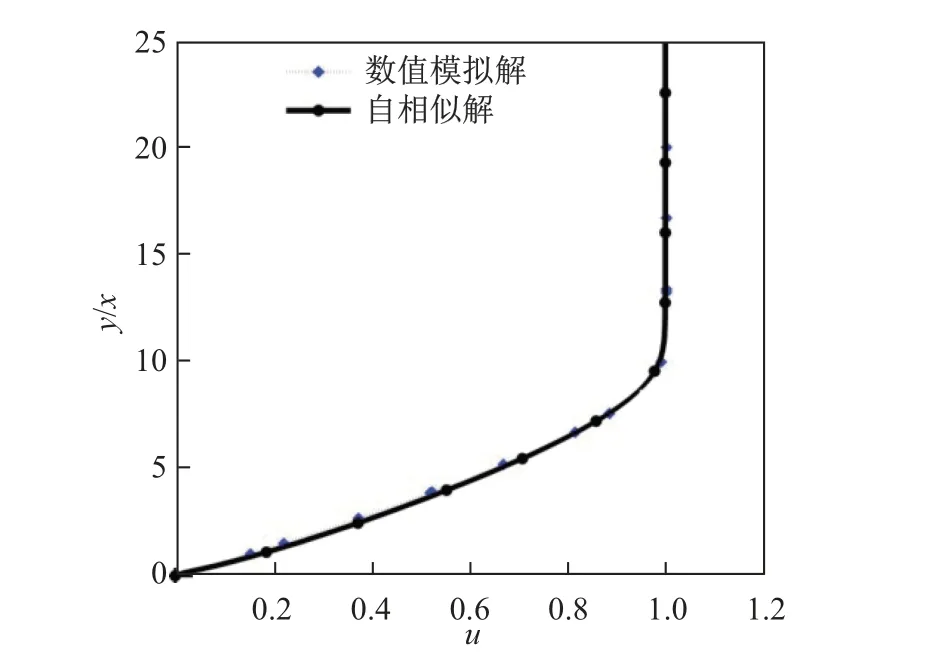
图4 平板上超声速流动边界层上的速度分布Fig.4 Velocity distributions of the supersonic flow boundary layer on a plate
采用飞行高度为20 km 的后台阶流动和射流相互作用流场进行网格无关化验证,以确定流场合适的计算网格. 选择y= 0 处的数据来验证网格无关性. 选择t= 0.015 s 对称线位置的静压曲线,使用了3 种不同总数的网格(180 万,360 万和540 万). 图5 显示了不同网格的压力分布. 结果发现,3 种网格的结果吻合良好. 本工作选择总数为180 万的网格进行数值模拟.

图5 3 种网格的压力曲线变化Fig.5 Changes of the pressure curves under three kinds of grids
2 数值结果与分析
2.1 不同飞行高度下的超声速后台阶流动
在超声速后台阶流动中,超声速来流从两步后台阶两侧流过(见图6). 可以看出: 超声速来流经过后台阶上方壁面时,由于壁面附近气体速度梯度急剧变化,沿来流方向壁面起始处产生了微弱的前缘激波; 气体经过拐点时,几何外形发生突变产生分离形成剪切层,剪切层和台阶之间形成一个回流区; 回流区内气流速度小,动能转化为内能,温度较其他区域明显增大; 气体在经过台阶拐角时发生膨胀,气体静压急剧变小且流速大小和方向均发生改变,拐角附近形成膨胀扇区. 由于剪切层/激波作用,回流区内形成了涡结构,剪切层也因此扰动形成了激波(见图7). 图6 中3 种飞行高度下的流场结构类似,但当飞行高度为50 km 时,因为飞行高度的增加,密度和来流静压会有量级的降低,Re也会随之有量级的减小,尾涡有明显拉长的现象,剪切层的水平倾角也变小(见图6(c)).

图6 不同飞行高度下的后台阶流动密度梯度Fig.6 Supersonic flow acts on the double backward-facing steps at different flight altitudes

图7 20 km 飞行高度下的后台阶流动底部涡结构Fig.7 Vortex structure at the bottom of the double backward-facing step at 20 km flight altitude
回流区内气体流动速度较慢,并且有涡的相互作用,来流动能在回流区内转化为内能,壁面温度和来流温度产生了明显的差异,壁面温度相对于来流温度要高. 3 种飞行高度下的壁面温度接近,后台阶壁面BC,CD,DE 的温度为特征温度的2.3~2.7 倍(见表4).

表4 不同飞行高度下的后台阶流动的壁面温度Table 4 Wall temperatures of the double backward-facing step at different flight altitudes
2.2 不同飞行高度下的射流
射流从后台阶底部处产生后,首先经过一个三角形的等速核心区. 等速核心区内的温度、密度等都为常数且不会改变. 等速核心区外产生膨胀扇区,膨胀扇区沿着射流的流动方向逐渐变宽. 膨胀扇区的发展造成了射流宽度的增大和三角形等速核心区的线性收缩,如图8 所示.射流气体的膨胀使得气体加速并且速度方向发生改变. 同时,由于气体的膨胀引起射流边界附近的静压低于环境静压,使得射流气体在剪切层边界被压缩,形成反射激波和射流剪切层. 在不同飞行高度下,流场基本结构类似.
图9 为距离射流喷口0.05 处y方向半截面上的速度分布. 可以看出,3 种飞行高度的情况都属于高度欠膨胀射流形态. 流体首先经过等速核心区,在等速核心区内流体速度恒定,均约为无量纲速度2. 随后流体开始快速膨胀,形成对称的膨胀扇区. 射流在经过膨胀激波时加速并且速度方向发生改变,此时速度开始增加. 膨胀扇区外因为流体静压与周围环境静压不匹配,产生了拦截激波和剪切层,经过高强度的拦截激波和宽度较大的射流剪切层时,气体速度急剧下降.

图9 不同飞行高度下距射流喷口0.05 处半截面上的速度分布Fig.9 Velocity distributions on half section of jet flow at different flight altitudes(0.05 away from the nozzle)
不同飞行高度下膨胀扇区的大小有很大差异,尤其是在飞行高度为50 km 时气体的密度、静压与其他两个飞行高度相比有量级的降低,射流和环境气体的静压比也明显增加,射流边界张角增大,膨胀扇区大小也随之变大. 因此当飞行高度为50 km 时,速度在无量纲范围0.05<y <0.3 之间持续增加,而其他两种高度下的速度增加范围约为0.05<y <0.1(见图8). 该范围反映了膨胀扇区的大小. 3 种飞行高度下气体所能达到的最大速度均为射流初始速度的1.25~1.3 倍左右,且随着飞行高度的增加,最大速度也增加. 飞行高度为50 km 时对应的最大速度明显大于其他两种飞行高度.
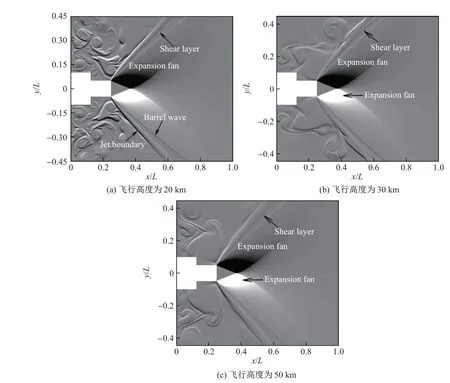
图8 不同飞行高度下的射流密度梯度Fig.8 Density steps of jet flow at different flight altitudes
随着飞行高度的增加,由于射流喷口静压与环境静压的比值显著增大,射流的强度显著增强,射流边界附近的剪切层水平倾角也随之增大,各飞行高度下的剪切层水平倾角如表5 所示,其中飞行高度为50 km 时的剪切层水平倾角最大,可达53.2°左右.

表5 不同飞行高度下的射流剪切层角度Table 5 Angles of jet flow shear layer at different flight altitudes
2.3 超声速来流/射流在后台阶的相互作用
以飞行高度为20 km 时超声速后台阶流动和射流相互作用的流场结构为例. 后台阶拐角处气体发生分离产生来流剪切层,来流剪切层和后台阶之间形成回流区. 回流区内复杂的涡结构造成了来流剪切层的扰动,并在剪切层上形成小激波(如图10(a)). 在射流起始的三角核心区外气体发生膨胀形成膨胀扇区,气体在膨胀扇区内的速度大小和方向均发生改变. 来流剪切层和射流剪切层交汇后发生相互作用,两个剪切层汇合为一道混合剪切层. 混合剪切层两侧形成了两个新的激波,两侧速度大小不同引发不稳定性,使得混合剪切层在后期失稳. 混合剪切层的失稳导致剪切层上产生了一些小激波结构,这些小激波结构被包裹在混合剪切层两侧的激波内. 如图10 所示,不同飞行高度下流场结构类似,射流的形态有差异,飞行高度越高,射流剪切层的水平倾角越大,膨胀扇区面积越大.

图10 不同飞行高度下超声速来流/射流相互作用的流场密度梯度Fig.10 Density steps of supersonic flow/jet flow interaction at different flight altitudes
两步后台阶两侧的超声速来流会对射流本身形态产生影响,使得射流提前出现失稳现象:超声速来流剪切层和射流剪切层发生相互作用产生混合剪切层,混合剪切层由于受到两侧来流和射流的双重影响容易产生失稳. 以往研究表明,射流轴线压力分布经过了典型的膨胀-压缩-膨胀的循环过程[22]. 以飞行高度为20 km 为例,将只有射流的工况和超声速来流/射流相互作用的工况下的射流轴线压力进行对比发现: 在超声速来流/射流相互作用的工况下,因为有超声速来流的影响,流场结构提前出现了膨胀-压缩-膨胀的射流结构,轴线压力出现了明显的波动现象,符合膨胀-压缩-膨胀的现象(见图11). 而在只有射流的工况下,由于计算域较小,射流并未出现膨胀-压缩-膨胀的现象.
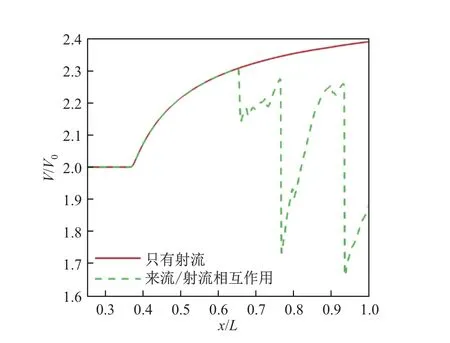
图11 20 km 飞行高度下只有射流和超声速来流/射流相互作用时的工况轴线速度分布Fig.11 Axial velocity distributions of only jet flow and supersonic flow/jet flow interaction at 20 km flight altitudes
当飞行高度为20,30 和50 km 时,选取超声速来流/射流相互作用和只有射流时距离射流喷口0.05 处半截面上的速度分布,结果如图12 所示. 首先射流气体经过三角形等速核心区,且在该区域内气体速度恒定. 随后流体开始快速膨胀,气体速度开始增加,当飞行高度为50 km 时,两种工况下的膨胀扇区大小都明显大于其他飞行高度,因此速度增加时的y范围明显大于其他飞行高度. 但由于超声速来流/射流的相互作用,超声速来流压缩射流,导致膨胀扇区小于只有射流的工况,尤其当飞行高度为50 km 时,超声速来流/射流的静压明显小于其他飞行高度. 来流对射流的影响显著,膨胀扇区受到来流压缩的影响明显变小,超声速来流/射流相互作用时速度增大的y范围明显小于只有射流时的速度增大范围.膨胀扇区外存在拦截激波和射流剪切层,气流经过拦截激波后速度急剧下降. 可以观察到,在飞行高度为50 km 的超声速来流/射流相互作用工况下,在穿过剪切层后速度会有波动. 这是因为已经到达了回流区,剪切层扰动导致回流区内产生大量的涡结构,从而造成速度的波动现象.
如图12 所示,超声速来流对射流的压缩,不仅会改变膨胀扇区的大小,也会对膨胀扇区内的最大速度产生影响(见图12). 在相同的飞行高度下,膨胀扇区内所能达到的最大速度,只有在射流的工况下略大. 在超声速来流/射流相互作用和只有射流两种工况下,同一飞行高度下的速度在等速阶段以后变大,两种工况下速度曲线基本吻合. 这说明膨胀扇区内气体膨胀的速率基本一致,有无超声速来流对于射流膨胀扇区的膨胀速率没有太大影响.
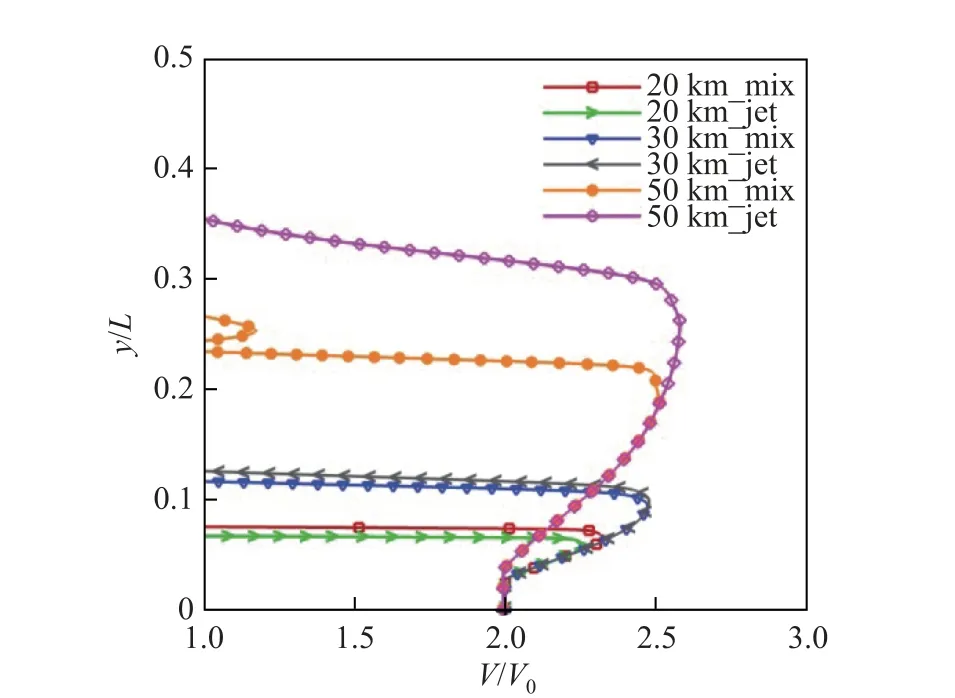
图12 不同飞行高度下只有射流和超声速来流/射流相互作用情况时距射流喷口0.05 处半截面上的速度分布Fig.12 Velocity distributions on half section of only jet flow and supersonic flow/jet flow interaction at different flight altitudes (0.05 away from the nozzle)
超声速来流对射流的影响主要有三个方面: ①超声速来流会压低射流边界和射流剪切层,使得射流膨胀扇区缩小,膨胀区内速度最大值也会变小,但对射流膨胀速率影响甚微; ②超声速来流和射流交汇后,两个剪切层会发生相互作用并汇合为混合剪切层,因混合剪切层两侧的速度不同而产生不稳定性,造成混合剪切层的失稳,形成一些小激波结构,改变了射流本身结构; ③混合剪切层两侧由于气体的压缩产生两个激波,两个激波的出现,使得射流内部的膨胀-压缩-膨胀现象提前出现.
射流剪切层的角度变化可以反映超声速来流对射流的压缩程度. 高度越高,来流静压越小,射流的影响相对变强,射流剪切层的水平倾角随着飞行高度的增加而增大. 如表6 所示,同一飞行高度下,超声速来流/射流相互作用时的射流剪切层水平倾角小于只有射流的情况. 当飞行高度为20 km 时,射流静压约为来流静压的3 倍左右,此时超声速来流的影响较大. 在超声速来流/射流相互作用的工况下,射流剪切层的水平倾角约为7°左右,而该飞行高度下只有射流工况下的射流剪切层水平倾角高达40°左右. 随着飞行高度增加,来流对射流的压缩效应变弱,剪切层的水平倾角也随之增大. 尤其当飞行高度为50 km 时,射流静压约为来流静压的250 倍左右,此时来流影响较小,超声速来流/静流相互作用后射流剪切层的水平倾角为41°,相比于飞行高度为20 km 时明显增大.

表6 不同飞行高度下的射流剪切层角度Table 6 Angles of jet shear layer at different flight altitudes
射流剪切层水平倾角变化对于流场结构产生的影响如图13 所示. 可以看出: 飞行高度增加,超声速来流的影响变小,射流影响相对变大,射流剪切层水平倾角变大,底部涡区会有明显的拉升. 对于不同飞行高度,由于射流剪切层和超声速来流剪切层水平倾角的变化,导致回流区大小和形态发生改变,进而影响回流区大尺度涡的数量. 在飞行高度为20 km 时,超声速来流静压要大于其他飞行高度,对流场结构的影响较大,此时超声速来流剪切层向下发展. 当飞行高度为30 km 时,超声速来流静压相对于20 km 时有所减小,对射流的影响变小,此时超声速来流剪切层抬升,基本呈水平状态. 上述两个飞行高度中回流区内大尺度涡结构丰富. 在飞行高度为50 km 时,超声速来流静压相对小于其他高度,射流在超声速来流/射流相互作用中占主导地位,射流剪切层水平倾角变大,进而抬高了来流剪切层,回流区明显变大,此时回流区内只观察到两个大尺度涡.

图13 不同飞行高度下超声速来流/射流相互作用时的底部涡结构Fig.13 Vortex structures of supersonic flow/jet flow interaction at different flight altitudes
超声速来流/射流相互作用会对回流区壁面温度产生影响. 与只有后台阶流动的工况相比,射流的存在使得回流区内涡结构相互作用更加剧烈,因而壁面温度也有明显提高. 选取两步后台阶回流区内BC,CD 两个壁面. BC 段温度如表7 所示,可见不同飞行高度下壁温约为来流温度的2.8~4.3 倍左右,且高度越高、温度越高,加热的效果越明显. CD 段温度如表8 所示,约为来流温度的4.0~5.3 倍左右. 与只有后台阶流动时的温度(见表5)相比,超声速来流/射流相互作用下BC,CD 的温度比只有后台阶流动时大得多.

表7 不同飞行高度下超声速来流/射流相互作用时的BC 段温度Table 7 Temperatures of BC section of supersonic flow/jet flow interaction at different flight altitudes

表8 不同飞行高度下超声速来流/射流共同作用时的CD 段温度Table 8 Temperatures of CD section of supersonic flow/jet flow interaction at different flight altitudes
3 结束语
本工作分别应用五阶精度WENO 格式、六阶精度中心差分格式离散对流项和粘性项,时间积分采用三阶精度Runge-Kutta 格式,研究了超声速后台阶流动、射流的基本流场结构,并进一步研究了超声速来流/射流在后台阶的耦合流动,得到如下研究结果.
(1) 在后台阶流动的工况中,气体经过后台阶拐角形成一个剪切层,剪切层后台阶之间的回流区涡造成了剪切层的扰动,使剪切层上方形成了激波. 当飞行高度为50 km 时,剪切层明显拉长.
(2) 在只有射流的工况中,射流首先经过三角形等速核心区,等速核心区外气体膨胀形成膨胀扇区,膨胀扇区外形成拦截激波和射流剪切层. 射流剪切层的水平倾角随着飞行高度的增加有小幅增大.
(3) 在超声速来流/射流相互作用的工况中,射流剪切层和超声速来流剪切层交汇并发生相互作用,形成一个混合剪切层. 混合剪切层两侧形成两道激波,混合剪切层上由于失稳产生小激波结构. 随着飞行高度的增加,射流剪切层明显增大.
(4) 在超声速来流/射流相互作用的工况中,有可能将射流气体卷入了两步后台阶的回流区中,对壁面形成显著的加热. 对两个剪切层相互作用的流场机理尚不成熟,需要在以后的工作中进一步研究.
