高增压柴油机进气流动理论研究

2021-02-26文明李玉峰贾孟秋鲁祯王天友

车用发动机 2021年1期

文明，李玉峰，贾孟秋，鲁祯，王天友

(1.天津大学内燃机燃烧学国家重点实验室，天津 300072；2.中国北方发动机研究所(天津)，天津 300400)

随着内燃机排放和油耗法规日益严格，越来越多的柴油机采用以高增压为特征的高强化技术，功率密度不断提升。例如，大众汽车公司开发的帕萨特2.0 L TDI柴油机采用250 MPa高压共轨喷油系统、高压压比和低压压比分别为3.8和1.5的二级增压系统，在标定转速4 000 r/min时升功率达88 kW/L[1]。德国FEV咨询公司针对单缸排量为0.4～0.5 L的轿车柴油机开发的高效燃烧系统(HECS)，采用增压比为3.8的单级VGT增压器，在4 800 r/min时升功率达到105 kW/L[2]；一些学者在进气压力0.3～0.4 MPa、喷油压力250～300 MPa工况下，在单缸柴油机上开展了升功率达100 kW/L的匹配试验研究[3-5]。

当增压比提高以后，发动机进气压差和空气密度显著增加，一些研究者认为[6-13]，进气流速和进气马赫数将随增压压比的提高而显著增加，也将造成气道缸内涡流比、湍流强度等宏观和微观流场参数随增压压比提高而显著增加。但是，实际发动机的进气流动是受周期性活塞运动制约的瞬态流动过程，比稳态流动状态复杂，因此弄清高增压柴油机进气流动规律对于进气道设计、缸内流动和燃烧组织都具有十分重要的意义。

本研究针对一台高增压单缸柴油机的实际运行条件，运用仿真方法对缸内流动进行试验标定并开展了计算分析，并进一步进行了理论分析，揭示了高增压柴油机的进气流动规律。

1 高增压柴油机进气流动的仿真研究

1.1 高增压单缸柴油机进气流动的试验参数

发动机为一台排量为1 L的单缸柴油机，采用4气门、喷油器中心布置、双顶置凸轮轴结构。此单缸柴油机主要性能和结构参数见表1。一个外源压气机提供所需进气压力，高压空气在进入气缸前先经过一个稳压箱以消除进气压力波动。通过缸压传感器测量气缸压力，通过进气压力传感器测量进气稳压箱压力(平均进气压力)和进气道入口处瞬态压力(瞬时进气压力)。试验台架见图1。

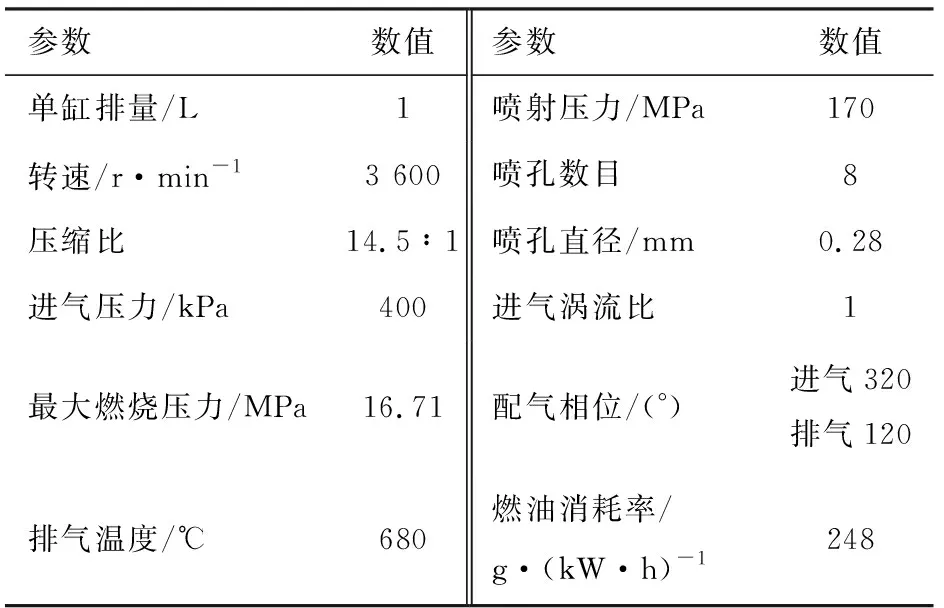
表1 高增压单缸柴油机参数

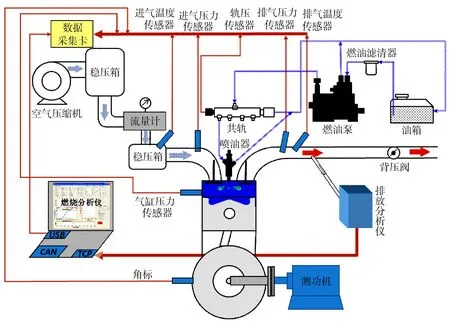
图1 发动机试验台架

由图2看出，在转速4 000 r/min的工况点上，稳压箱里的平均进气压力为400 kPa，进气过程中的最大进气压差可达80 kPa，大致位于进气冲程中部活塞速度变化率最大的位置。

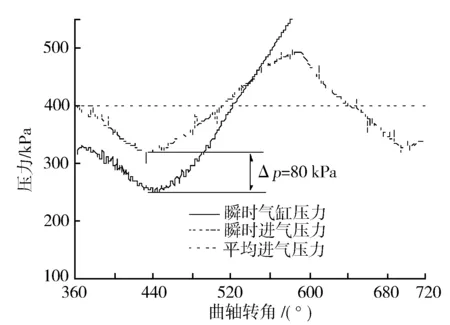
图2 进气压差变化

1.2 模型建立

本研究采用的柴油机瞬态计算模型是以上述单缸柴油机缸盖为基础建立的(见图3)，包括进/排气道、进/排气门、气缸盖和燃烧室，采用切向气道与螺旋气道组合的双进气道，在后续分析中会分别对切向气道和螺旋气道侧气门处的流场进行分析。

采用商业软件Converge对增压柴油机进气门处流动特性展开研究。本研究采用的网格策略见图4。模型基础网格尺寸为4 mm，气缸上部、进气道和进气门附近区域采用固定加密对网格进行了细化，加密等级各有不同，最小网格尺寸为0.25 mm，位于气门阀座区域，平均网格尺寸为1.1 mm。模型在上止点的总网格数约为68万，在下止点约为120万。亚格子湍流模型为k方程模型，近壁区域采用Werner and Wengle近壁模型进行求解。

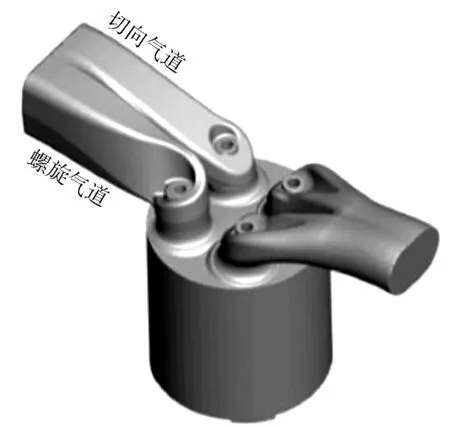
图3 发动机进气流动几何模型

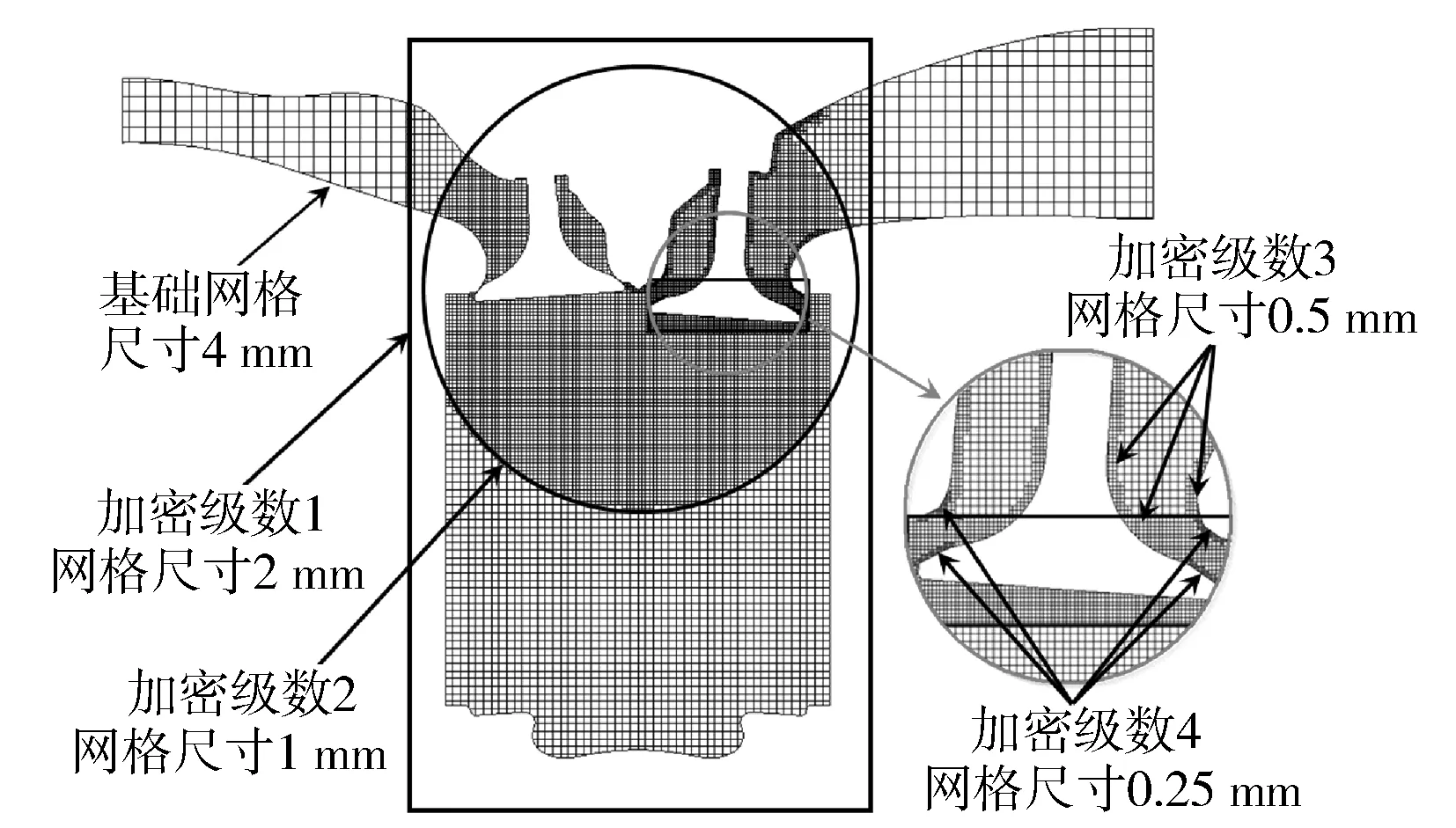
图4 计算网格示意图

1.3 计算工况及边界条件

为对比不同增压比与转速对气门附近流动的影响，本研究设置了6个算例，如表2所示。每个工况的算例都计算23个循环，考虑到初始条件的影响，前3个循环被剔除，只对后20个循环的数据进行分析。针对单缸机转速为3 600 r/min、增压比为3.2的试验工况，对热力学单缸机试验的不着火缸压曲线进行了仿真标定，标定结果用于后续的数据分析。

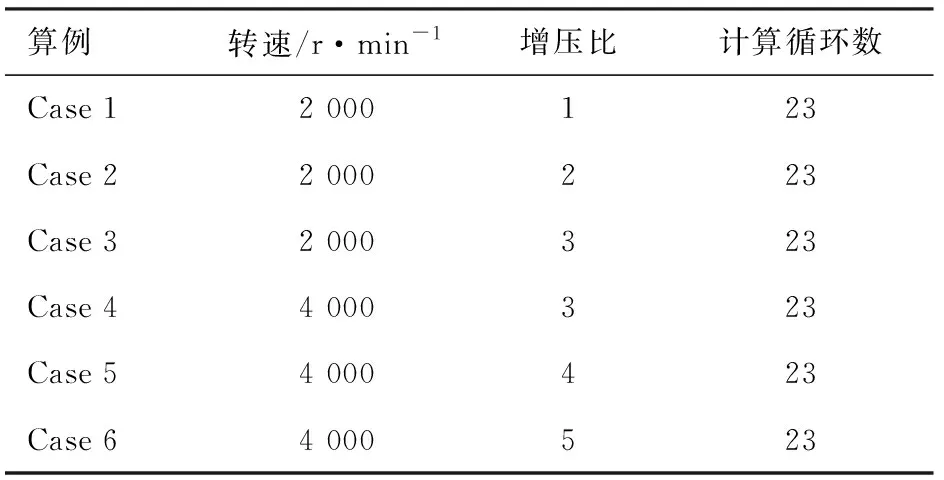
表2 计算工况

柴油机几何模型的进口边界与出口边界均设为压力边界，其中进口压力的设置随增压比而变化，如增压比为1时进口压力设为101 325 Pa，增压比为2时进口压力设为202 650 Pa，以此类推。出口压力在所有工况下都设置为101 325 Pa。进气道与进气门壁面温度设为300 K，排气道与排气门壁面温度设为320 K，气缸盖、气缸套和活塞顶部的壁面温度设为350 K。

1.4 模型试验标定

对转速为3 600 r/min、增压比为3.2工况的单缸机缸压曲线进行标定，模拟计算中未考虑燃烧过程，因此，只对压缩上止点前缸压曲线模拟值与试验值的相对误差进行了分析，结果见图5。由图5可知，进气与压缩过程中缸压的模拟值与试验值曲线符合良好。在压缩上止点前，模拟与试验的相对误差最大为0.93%，可知本研究中的仿真结果是真实可靠的。

图5 热力学单缸机试验与仿真缸压曲线对比

2 仿真结果分析

2.1 进气压差和气缸空气量的变化规律

图6示出在不同转速和增压比条件下进气压差随曲轴转角的变化。由图6可见，在进气上止点(360°)附近，由于进气门开度很小，进气压差较大，在转速2 000 r/min、增压比3时进气压差高达180 kPa。在活塞下行的主要进气过程中(390°～540°)，发动机转速和增压比都对进气压差有明显的影响，转速2 000 r/min时的进气压差比转速4 000 r/min的进气压差小得多；当转速较低(2 000 r/min)时，进气压差随增压比的增加变化较小，而当转速较高(4 000 r/min)时，进气压差随增压比的增加显著提高；在转速为4 000 r/min、增压比为5时，最大进气压差可达90 kPa，大致位于进气过程中期活塞速度变化率最大的曲轴转角位置，即图6中的450°。这一结果也与图2所示的试验结果一致。

图7示出不同转速和增压比下进入气缸的空气质量随曲轴转角的变化。由图7看到，增压比对进气质量的影响较大，进气质量随增压比的提高而显著增加；转速对进气质量的影响较小，在增压比为3时，当转速从2 000 r/min提高到4 000 r/min，在主要进气过程中(390°～540°)，低转速的进气质量稍高于高转速的进气质量，这是因为发动机在较低转速下的充气效率比高转速下的充气效率要高一些。

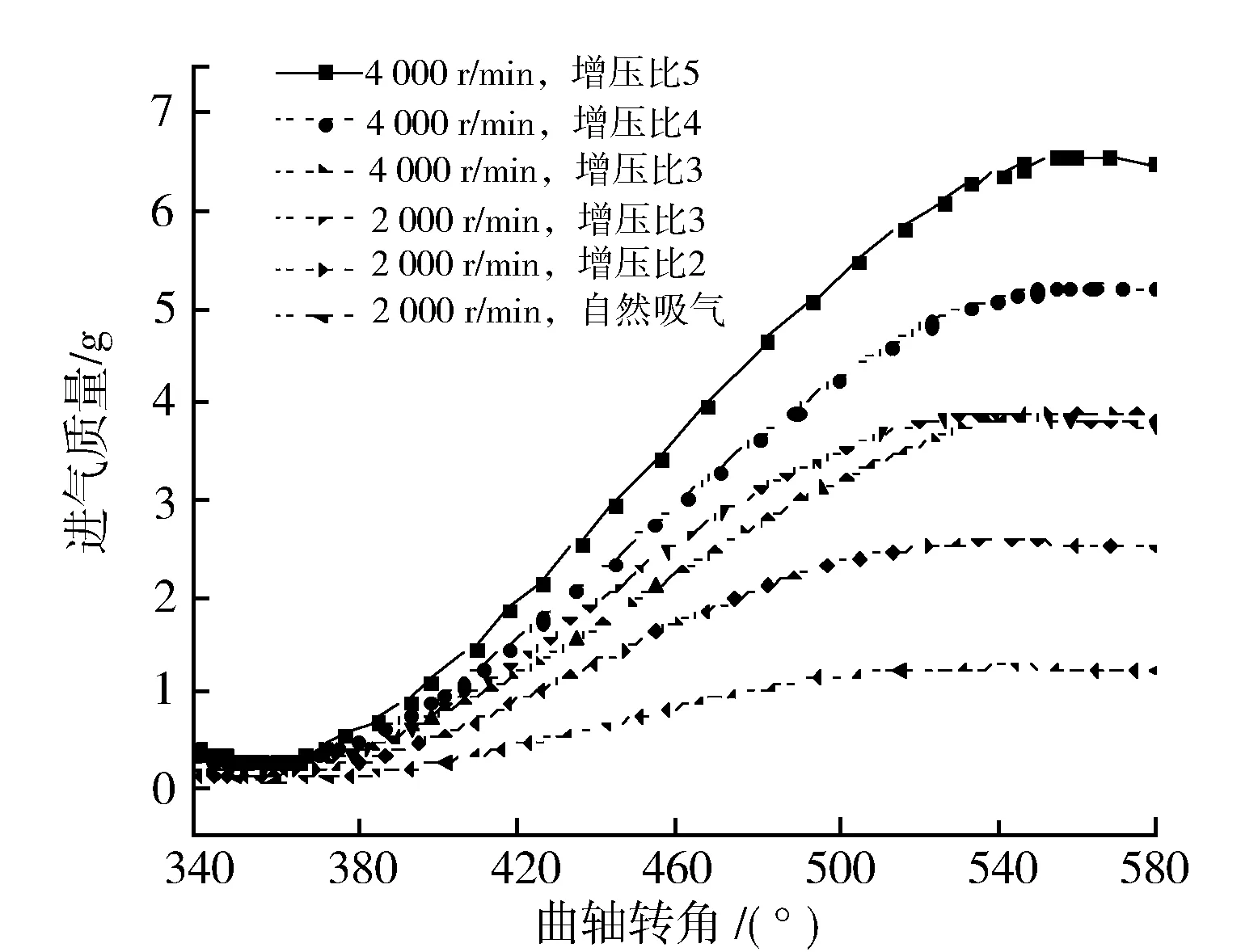
图7 进气质量随曲轴转角的变化

2.2 气道进气射流相对轴向速度的变化规律

当进气气流在一定压差作用下流过进气门与阀座形成的环形区域时，形成了进气射流。为了便于描述进气射流的速度方向及分布，图8示出进气射流的3个速度方向和气门阀座圆周方向的起始角度。为了便于数据分析，如不是特指进气射流在气门-阀座环形区域的空间分布时，都把给定圆周角度上对应计算点的进气射流速度进行算术平均，形成了平均进气射流速度随阀座圆周角度的变化规律。

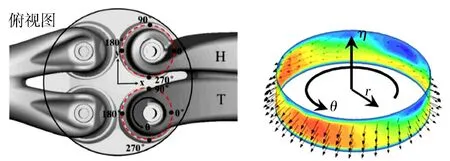
图8 进气射流速度方向和分布角度定义

图9示出在转速2 000 r/min、不同增压比条件下，在进气过程中期切向气道进气射流的相对轴向速度沿阀座圆周方向的变化规律。相对轴向速度是指进气射流的轴向速度分量(Vtotal)η(给定圆周角度上对应的进气射流速度进行算术平均)与平均活塞速度Sp之比。由图9可见，2 000 r/min时，在进气过程的中期(460°)，进气射流相对轴向速度沿圆周方向的分布变得非常不均匀，与气道相对的阀座部分(180°周围)获得较高的速度；但进气射流的相对轴向速度数值及其沿阀座圆周方向的分布规律均不随增压比的增加而变化。在进气过程中进气射流在其他方向上速度分量随增压比的变化规律与此相似。此外，螺旋气道出口的进气射流速度随增压比的变化规律也与切向气道的相似，即在进气过程中，进气射流速度大小及其沿阀座圆周的分布规律几乎不随增压比增加而变化。

图9 不同增压比条件下进气射流相对轴向速度分布(460°(进气冲程100°)，切向气道，2 000 r/min)

图10示出转速4 000 r/min、不同增压比条件下，在进气过程中期切向气道进气射流的相对轴向速度沿气阀座圆周方向的变化规律。由图10可见，在进气过程中期(460°，活塞最大运动速率附近)，相对轴向速度数值及其沿阀座圆周的分布规律几乎不随增压比的提高而变化。

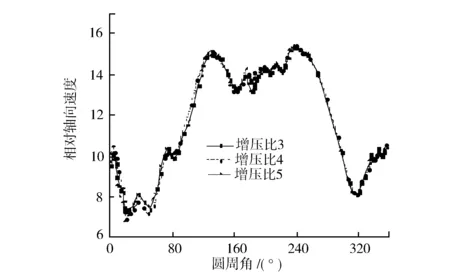
图10 不同增压比条件下进气射流相对轴向速度分布(460°(进气冲程100°)，切向气道，4 000 r/min)

图11示出转速4 000 r/min、进气行程460°、不同增压比时，切向、螺旋两个气道出口的进气射流相对轴向速度沿其阀座圆周方向的空间分布。由图11看到，在两个气道出口的环形区域内进气射流的相对轴向速度空间分布规律几乎不随增压比的变化而变化。

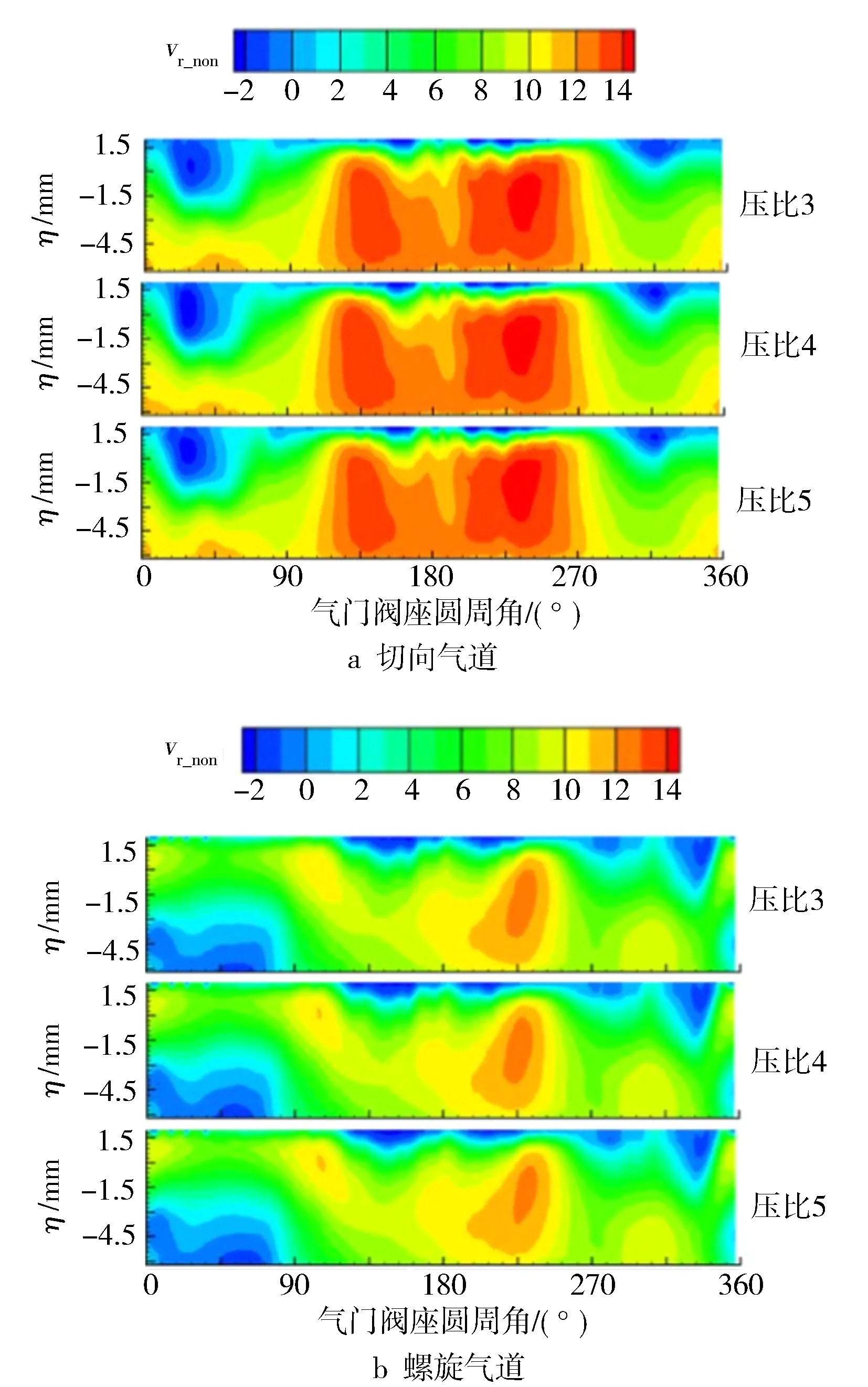
图11 在两个气道出口处进气射流的相对轴向速度的空间分布(460°)

2.3 缸内涡流比和平均湍动能的变化规律

图12示出在不同转速和增压比条件下进气和压缩过程中缸内涡流比随曲轴转角的变化规律。由图12可见，对于4 000 r/min转速，在进气和压缩过程中缸内涡流比的大小及其随曲轴转角的变化几乎不随增压比的变化而变化；转速2 000 r/min时，除自然吸气进气方案外，增压比2和增压比3进气方案的缸内涡流比的大小及其随曲轴角度的变化规律也几乎不随增压比的变化而变化。

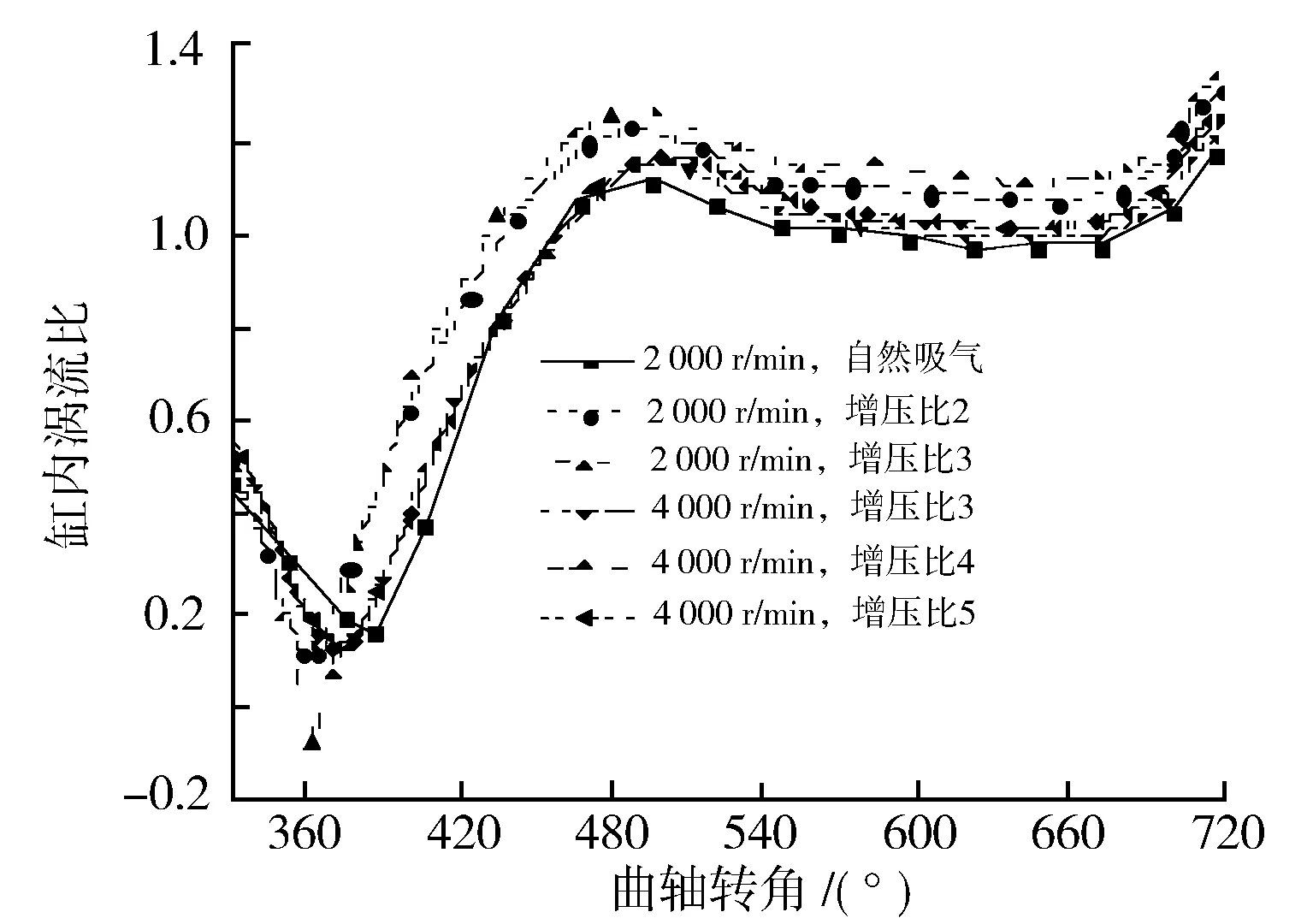
图12 缸内涡流比随曲轴转角的变化

图13示出不同转速、不同增压比条件下进气和压缩过程中缸内平均湍动能随曲轴转角的变化规律。由图13可见，除自然吸气进气方案外，在进气和压缩过程中缸内平均湍动能的大小及其随曲轴转角的变化规律几乎不随增压比的变化而变化。

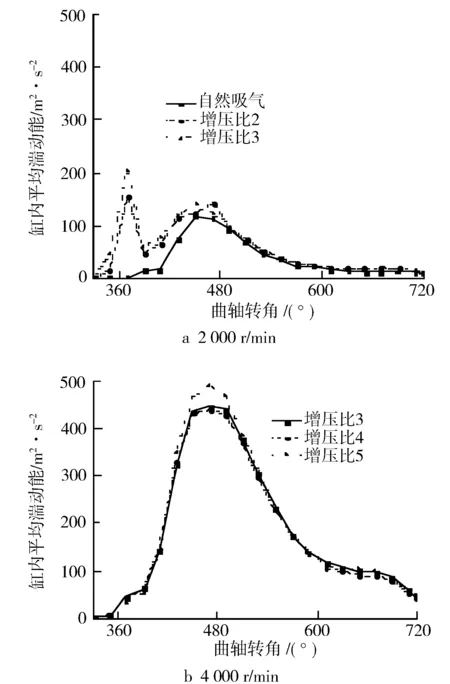
图13 缸内平均湍动能随曲轴转角的变化

综合上述仿真计算结果的分析可以得出，高增压柴油机在相同转速工况下，虽然进气压差随增压比提高而显著增大，但进气射流速度的大小及其分布、缸内涡流比、缸内湍动能等宏观和微观流动参数基本上不随增压比的提高而变化，缸内湍动能随转速的增大而增大。

3 高增压柴油机进气流动的理论分析

按照流经气阀座的进气射流和活塞扫过的气缸容积来表达平均进气质量流率：

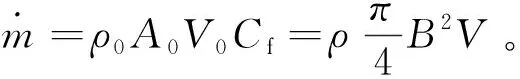
(1)

式中：ρ0和ρ分别为进气阀座处和缸内的空气密度；Cf为气道流量系数；A0为进气门与阀座之间的环形面积；B为缸径；V0和V分别为进气射流速度和平均活塞速度。其中，四冲程发动机的平均活塞速度可由下式获得：

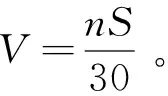
(2)

式中：n为发动机转速；S为冲程。

假设进气过程为绝热过程，则

(3)

式中：p0和p分别为进气阀座处的压力和缸内压力。

由式(1)和式(3)可知，

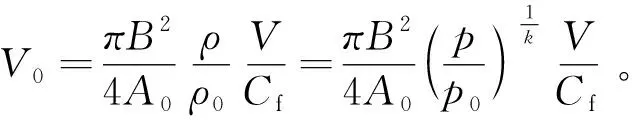
(4)

式(4)表示进气射流速度V0受限于平均活塞速度V，且与气道流量系数、进气压力与缸内压力比值有关。当发动机转速一定时，平均活塞速度V是一个定值。假设在转速、进气压力一定的条件下，增压比从一个数值a提高到另一个数值b，由式(4)推出：

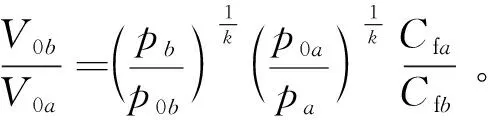
(5)

式中：下标a，b分别表示增压比a和增压比b时对应的参数。

由于发动机进气压力与缸内压力之比按照某一种热力过程(常常假设为绝热过程)规律变化，因此当进气压力从一个状态变化到另外一个状态时，式(5)中前两项之积等于1，这样，进气射流的速度之比反比于气道流量系数之比，即

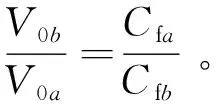
(6)

由式(1)可知，在发动机转速一定的条件下，当增压比从数值a增加到数值b时，其进气质量与进气密度、气道流量系数和进气流速的关系如下：

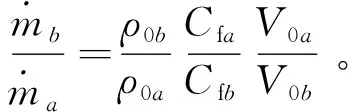
(7)

依据式(6)，式(7)中后两项的乘积为1，因此式(7)可以推导成：

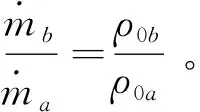
(8)

这个结果说明，对于高增压发动机，当增压比提高时，进气质量的增加主要源于进气密度的增加。

将增压比从一个压比增加到另一个压比，依据图7得到进气质量增加率，依据理想气体公式计算得到进气密度的增加率，结果见图14。在发动机转速4 000 r/min时，当进气压力从0.3 MPa分别增加到0.4 MPa和0.5 MPa时，除进气初期(340°～410°)数据波动之外，在绝大多数进气过程中，进气质量的增加率几乎等于进气密度的增加率；转速2 000 r/min时，当进气压力从0.2 MPa增加到0.3 MPa时，除进气初期(340°～410°)数据波动之外，进气质量的增加率几乎等于进气密度的增加率。由此可知，当增压比提高时，进气质量的增加主要源自于进气密度的增加。

图14 进气质量、进气密度和流量系数的增加百分数随增压比增加的变化规律

高增压柴油机中由于循环油量和循环气量大幅度增加，在进气组织中需要提高空气的动量和能量来促进混合气的形成。从前面分析得知，当增压比提高后，进气流速u、缸内涡流比、缸内湍流强度u′或湍动能1/2u′2等宏观和微观流场参数均不随增压比增加而增加，空气运动对油气混合的作用不随增压比的提高而加强。但是考虑到进气密度随增压比增加而增加的事实，那么单位体积的流动动量ρu、动能1/2ρu2以及脉动动量ρu′、脉动动能1/2ρu′2均随增压比的提高而显著增大，为高增压发动机的油气混合过程提供了更大的流动动量和脉动动能。