基于改进的DQN机器人路径规划

董永峰，杨 琛，董 瑶+，屈向前，肖华昕，王子秋

(1.河北工业大学 人工智能与数据科学学院，天津 300401；2.河北工业大学 河北省大数据计算重点实验室，天津 300401；3.河北工业大学 河北省数据驱动工业智能工程中心，天津 300401)

0 引 言

移动机器人的研究已经成为当前社会和科技的研究方向，路径规划技术是机器人研究中的基础问题[1]。硬件技术的进步促进了机器人路径规划算法的发展，包括传统算法，例如：遗传算法[2]、蚁群算法[3]、强化学习[4]。还有另一种新颖的方法，深度强化学习[5]，该方法是深度学习与强化学习的结合，深度强化学习解决了强化学习中状态到动作映射所带来的维数灾难问题[6]，能更好满足机器人动作选择需求。

Google DeepMind中Mnih等提出深度Q网络模型[7]，该模型将深度网络和Q-learning算法结合，不仅解决了传统Q-learning算法中的维数灾难，也可以机器人所获取的环境信息作为训练数据训练网络，达到网络收敛[8]。Tai Lei等[9]将DQN算法应用到了移动机器人的路径规划中，但是在实验过程中，出现了过估计对机器人动作选择带来的负面影响，造成机器人获得的奖赏值和规划出的路径并非最优。在DQN的基础上又出现了很多改进的算法，比如深度双Q网络[10]、竞争深度Q网络[11]、优先回放DQN[12]、平均DQN[13]等。DDQN有效解决了DQN在实验环境下存在Q学习算法固有的缺点——过估计问题[14]，使得智能体能够选择相对较优的动作。但是DDQN优化目标中，仅仅利用当前估计网络参数，忽略了先验知识的重要性。在前期的网络训练中，网络参数均为初始化，并未进行网络训练，即不存在先验知识，若是利用平均DQN优化目标进行估计网络参数训练，会使得网络参数训练效率降低。

为了更有效解决深度Q学习算法中的过估计问题，本文提出一种DTDDQN算法，融合平均DQN和DDQN的各自优点，来减少过估计对移动机器人动作选择的影响，实现最优动作策略的选择。

1 深度强化学习

1.1 深度Q学习

在Q-learning算法中，利用一个Q值表来对状态-动作值函数进行存储和更新，并根据机器人所学习的经验知识对Q值表进行更新。然而随着机器人所处环境状态复杂程度的升高，使用Q值表存储状态-动作值函数的短板越发明显，将会引起“维数”灾难。为解决Q-learning随着环境复杂程度的升高而带来的“维数”灾难，可以利用函数近似逼近来替代Q值表并对值函数进行计算。函数逼近可以是线性函数逼近或者是非线性函数逼近，比如利用深度学习中的神经网络，我们可以称之为深度Q网络(DQN)。

DQN是Q-learning算法的一种改进算法，它以神经网络作为状态-动作值函数的载体，用参数为θ的f网络来近似替代状态-动作值函数，公式如式(1)所示

f(s,a,θ)≈Q*(s,a)

(1)

其中，f(s,a,θ)可以是一种任何类型的函数，通过函数来近似替代Q值表，无论输入空间有多大，都能够用神经网络的输出值计算Q值。在深度Q网络中，存在两个网络，分别为估计网络和目标网络，两个网络的结构完全相同，不同之处在于网络参数。其中估计网络的输出为Q(s,a,θ)，用来估计当前状态动作的值函数；目标网络的输出表示为Q(s,a,θ-)。网络参数更新规则为，估计网络中的参数实时进行更新，在经过C步之后，估计网络的参数会复制到目标网络中。DQN网络更新是利用TD误差进行参数更新。公式如式(2)所示

Lt(θt)=E(yt-Q(s,a,θt))2

(2)

其中，yt为优化目标，计算公式如下

(3)

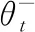
DQN中训练网络所用的样本集来自于经验池中，在移动机器人与环境交互后，会将交互后的转移样本(st,at,rt,st+1)存储到经验池D中。每次的网络训练会从经验池D中取出一定数量的转移样本集，采用随机梯度下降的方法进行网络参数的更新。

1.2 深度双Q学习

Van Hasselt等发现在实验过程中，DQN在Q值的计算中，存在过估计的问题，即网络输出的Q值高于真实的Q值。为有效解决过估计问题，Van Hasselt等对DQN的优化目标进行优化改进，利用估计网络输出s状态下的Q值计算出对应Q值最高的动作a，再利用目标网络输出Q值计算优化目标并进行网络训练。DDQN利用估计网络进行动作选择，目标网络进行策略评估，将动作选择和策略评估进行了分离，有效解决了DQN中存在的过估计问题。其优化目标的更新函数如式(4)所示

(4)

2 改进的算法

2.1 过估计问题

通常引起估计值函数和真实值函数之间误差有两方面：函数模型的不灵活性和环境中的噪声。深度Q学习的基本框架仍然是Q-learning算法，深度Q学习只是利用神经网络来代替table表来记录状态动作函数，所以深度Q学习无法克服Q-learning算法本身固有的缺点—过估计。

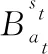
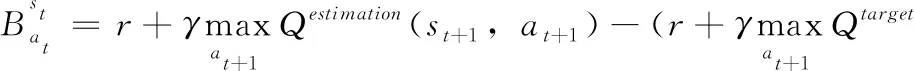
(5)

2.2 DTDDQN算法

假设在状态s下，机器人有动作a1,a2可以进行选择并执行，其中对应的真实的值函数为Q(s1,a1),Q(s2,a2)，并且在真实值情况下Q(s,a1)>Q(s,a2)，说明动作a1为状态s下的最优动作，动作a2为状态s下的次优动作。由于模型输出存在过估计，则有可能出现值函数Qestimation(s,a2)误差幅度大于值函数Qestimation(s,a1)误差幅度，从而导致模型输出的值函数Qestimation(s,a2)大于值函数Qestimation(s,a1)，由于机器人选择策略为greedy策略，所以在该情况下机器人所选择的动作为次优动作a2，而并非最优动作a1，造成机器人最终选择的策略并非最优。

在深度强化学习中，一种改进的方法是利用减少目标近似误差(target approximation error，TAE)来减少过估计对动作选择的影响，目标近似误差指的是目标期望值与估计网络的输出值的差值。公式如式(7)所示

(6)

(7)

引起目标近似误差TAE的原因有两个：第一个是损失函数不精确的计算影响到了参数的训练；第二个是经验回放缓冲区的大小有限，看不见状态动作对的泛化误差。为了有效解决过估计在路径规划中的影响，需要减少TAE的值。利用先前参数的网络对优化目标值进行计算取平均并进行网络参数的训练则能够有效减少TAE的值，从而解决深度强化学习在路径规划中的过估计问题[15]。

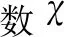
(8)

(9)

(10)

其中，式(10)为利用先前K代的参数计算出来的Q值的平均，动态融合后的优化目标更新网络参数能够减少目标近似误差，从而有效避免在动作选择时过估计问题的影响。利用改进后的优化目标进行TD误差计算，然后利用损失函数进行网络参数的更新，本文网络参数更新具体公式为

(11)

本文DTDDQN算法流程见表1。

表1 DTDDQN算法流程

3 基于DTDDQN的机器人路径规划

移动机器人的路径规划是机器人在与陌生环境的不断的交互学习中规划出一条避开障碍物最优路径。本文提出了一种DTDDQN算法，并将该算法用于机器人的路径规划。本文DTDDQN算法的训练模型如图1所示。

图1 DTDDQN算法模型

首先，机器人在陌生的环境中不断的学习并采集样本，用机器人当前所处状态的特征作为网络输入，将当前位置下的Q值作为网络输出，并利用动作选择策略进行动作选择，到达下一个状态，并将该系列的数据存储到经验回放池D中作为网络训练的样本。机器人在探索环境的最优路径过程中，不断利用改进的优化目标进行网络参数的更新，一直循环迭代直到训练完成。

在实验中，为了减少机器人所规划出的路径长度，本文中的实验机器人能够采用8个方向动作，如图2所示，动作1、2、3、4、5、6、7、8分别表示向上、右上、向右、右下、向下、左下、向左、左上。

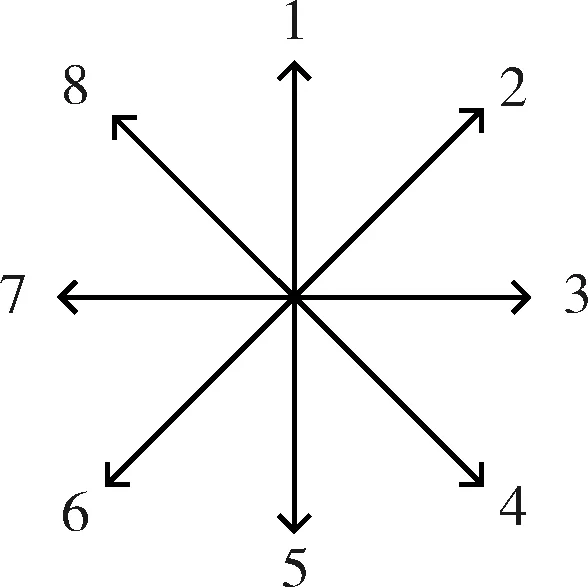
图2 方向图

在强化学习中，奖惩函数是影响路径规划的重要因素。在路径规划中，机器人的目的为最大化从初试状态到目标状态的累积回报期望。因此，奖惩函数直接影响路径规划的结果。在实验中，机器人碰到障碍物将会获得-1的惩罚值，到达自由栅格将获得1的奖赏值，到达终点获得5的奖赏值。本文的奖惩函数公式如下

(12)

4 实验结果与分析

4.1 实验环境和参数配置

本文在栅格法环境下进行两组路径规划实验，DTDDQN、DDQN、DQN这3种算法的迭代次数均为5000次，机器人到达终点为一次迭代的结束标志：

(1)实验一：与传统算法对比。环境为20×20的栅格环境。起始点位置为S点，目标点位置为E点，栅格图的环境如图3(a)所示。该环境为文献[16]中的环境。

(2)实验二：与DQN和DDQN算法对比。环境为20×20的栅格环境。起始点位置为S点，目标点位置为E点，与实验一环境进行对比，该环境障碍物分布复杂且不均匀。栅格图的环境如图3(b)所示。

其中黑色的栅格表示环境中的障碍物区域，白色的栅格表示环境中非障碍物可移动区域。

图3 栅格环境

实验环境为Windows下的频率为2.6 GHz的CPU服务器，网络框架为Tensorflow 1.8.0，选用python3.5.2版本进行编程实现。

本文算法与DQN、DDQN两种算法进行对比。3种算法的网络模型结构均为5层：输入层为机器人所在环境的特征向量；隐藏层有3层，每层有30个神经元，各层的激活函数均为relu函数；输出层为机器人所处环境状态下的Q值，Q值的维数为可执行动作的个数(即8维向量)。本文对比实验的超参数配置见表2。

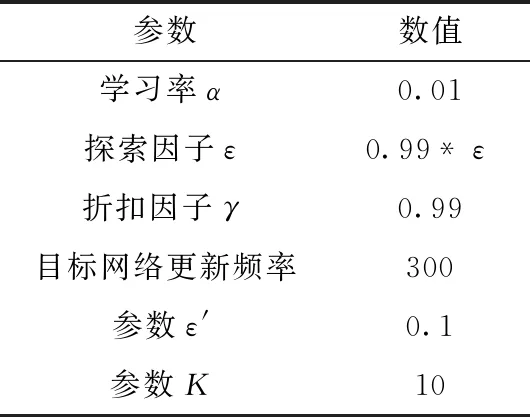
表2 参数设置

在本文路径规划训练过程中，探索因子初始化为1，采用模拟退火原则，每次迭代后乘以0.99，最后趋于0.1。模拟退火的原则可以使得机器人充分探索陌生的环境，获得充足的样本来训练稳定的网络，最终规划出一条更优的路线。

4.2 实验结果对比分析

4.2.1 与传统算法对比

本文DTDDQN算法在文献[16]的栅格环境下与改进的蚁群算法的文献[16]、文献[17]、文献[18]进行对比，对比指标包括以下两个：一是规划出的路径长度；二是规划出的路径拐点数。所得路径规划线路图如图4所示，指标对比数据见表3。

图4 4种算法路径规划

表3 4种算法对比

从表3和图4可以得出，在路径长度上，DTDDQN算法和文献[16]、文献[17]、文献[18]这4种算法规划出的路径长度均为28.627，但是本文的DTDDQN算法规划的路径拐点数为4，而文献[16]、文献[17]、文献[18]规划的路径拐点数分别为6,7,5。在实际的环境下，本文路径规划路线拐点数的减少也会减少机器人从起始点到目标点所用的时间。

4.2.2 与DQN、DDQN对比

本文在多种指标下与DQN、DDQN算法进行对比，其中包括机器人执行某一动作所能获得的奖赏值，该指标越高说明机器人能够在特定的环境下选择更优的动作。二是网络参数训练过程中机器人碰撞障碍物次数、算法所规划出路径的长度和拐点数。

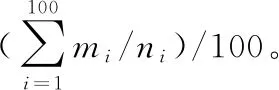
图5 平均每步奖赏值对比

表4 平均每步奖赏值对比

从图5和表4可以看出，在大多数情况下，DTDDQN算法的平均奖赏值都在DDQN和DQN之上，DTDDQN算法在训练过程中的平均奖赏值为1.013，而DDQN算法和DQN算法分别为0.957和0.911。DTDDQN的平均奖赏值比DDQN高出6%，比DQN高出10%，说明在躲避障碍物上和动作选择方面，DTDDQN算法比DDQN算法和DQN算法能够提供更好的行动策略。

图6(a)、图6(b)、图6(c)分别是经过5000次迭代后，DQN、DDQN、DTDDQN算法按照网络输出的最大Q值所对应的动作所规划出的路线图。从路线规划图和表5中得出，DQN、DTDDQN、DDQN算法均能规划出了一条无碰撞的路线。

图6 3种算法路径规划

从表5和图6可以看出，在路径长度上，DTDDQN算法规划出了一条最优路径，路径长度为28.627，拐点数为8，而DQN、DDQN算法并未规划出一条最优路径，DDQN算法规划的路径长度为29.213，拐点数为11。最差的是DQN算法，DQN算法规划出的路径长度为30.385，拐点数为10。在训练中，DTDDQN算法中的机器人障碍物碰撞次数为21 640次，而DDQN和DQN训练中机器人的碰撞次数分别为25 471次和28 182次。DTDDQN算法与DDQN、DQN算法障碍物碰撞次数相比，分别减少了18%、30%的碰撞次数。由此可以看出，与DQN、DDQN算法相比，DTDDQN算法在陌生的环境和在减少碰撞次数的条件下，能够规划出一条更优的路线。

表5 指标对比

5 结束语

本文提出的DTDDQN算法动态融合了DDQN和平均DQN各自优点，DTDDQN算法前期先以较大权重的DDQN优化目标对网络参数进行更新并进行先验知识的积累，到网络训练的中后期，增大平均DQN优化目标的更新的权重，从而充分利用先验知识进行网络训练，在减少TAE值的同时，使得网络输出的Q值更加接近真实Q值，以减少过估计对机器人在选择动作时的影响，达到所选动作策略最优。经过不同环境的仿真实验验证，DTDDQN算法较DQN算法和DDQN算法在训练过程中障碍物碰撞次数和平均奖赏值以及规划出的路径长度方面都有一定程度的提升和优化。