基于支持向量数据描述的闭合超球面机

梁锦锦

(1.西安石油大学 理学院，陕西 西安 710065；2.陕西师范大学 教育学院，陕西 西安 710062)

0 引 言

支持向量数据描述(support vector data description, SVDD)被广泛用于单值分类和奇异值检测[1,2]。文献[3]利用模糊C均值找到关键特征进而构造一种高效SVDD算法；文献[4]将SVDD应用于无线传感器网络；文献[5]对癌症多分类基因数据集，利用SVDD设计递归策略消去冗余特征；文献[6]对特征进行排序，构造多个支持向量数据描述模型；文献[7]对雷达目标识别问题，构造一种最小二乘SVDD模型，降低了计算复杂度且保证了检测精度；文献[8]修改SVDD的目标函数，并利用启发式策略解决参数选择问题，提高求解线性方程组的训练速度；文献[9]利用支持向量数据描述构造一种分类器SVDC，利用一类样本的球形描述边界对数据进行分类；文献[10]针对多源样本，利用支持向量数据描述构造一种多分类器；文献[11]融合支持向量数据描述和二叉树结合构造了一种多分类器，取得了良好的分类结果；文献[12]利用SVDD构造两个支持向量超球，避免了矩阵求逆的运算，提高了传统SVDD的分类器。这些研究或拓宽SVDD的应用领域，或构造快速训练算法，但由于训练仅利用目标类样本而不考虑非目标类样本，故而分类精度并不高。

从提高分类精度角度，笔者利用SVDD构造闭合超球面机(sealed hypersphere machine，SHM)，在SVDD的目标函数和约束条件中加入对非目标类样本的错分惩罚和限制条件，修正最小包围超球的描述边界，以更加准确地贴近实际的分类曲面，判断待测样本的类别。

1 闭合超球面机

1.1 支持向量数据描述SVDD

记{xi}(i=1,…,N)为n维空间Rn中的目标类样本，SVDD求取一个半径最小的超球来覆盖全体目标类样本。由于样本并非总是球形分布，SVDD通过非线性映射Φ:x→Φ(x)将样本投影到一个高维的特征空间。SVDD对样本xi引入松弛变量i≥0以放松约束条件，并引入正比于违反约束总量i的惩罚参数C>0。记最小包围超球的半径和球心分别为R和a，SVDD在非线性空间中求解如下凸二次规划

(1)

SVDD采用Lagrange乘子法，求解式(1)的对偶规划得到原问题的解

(2)

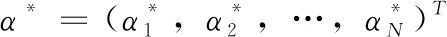
最小包围超球的球心按照下式进行计算

(3)

最小包围超球半径根据下式计算

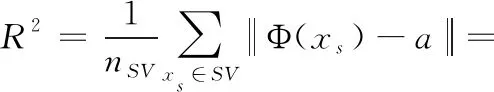
(4)

给定测试样本z，采用下列规则判断是否接受该样本

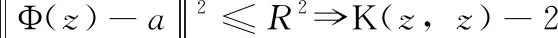
(5)

如果待测样本z到最小包围超球球心的距离平方小于超球半径R2，接受该测试样本为目标类；否则，拒绝该样本，将其作为非目标类。需要指出，这里距离的计算是在非线性空间中进行。

1.2 闭合超球面分类机SHM

以非线性空间为例，记Φ:x→Φ(x)为非线性映射，i,j≥0为松弛变量，C1,C2>0为惩罚参数，训练SHM等价于求解如下凸二次规划

(6)

采用Lagrange乘子法推导上述问题的最优解，依次对规划(6)中的4个不等式约束引入Lagrange乘子αi≥0,βj≥0,γi≥0和ηj≥0，构造如下Lagrange函数

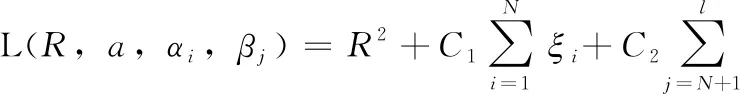
(7)

对Lagrange函数L(R,a,αi,βj)关于变量R，a，i和j求偏导，并置偏导的值为零，则有

(8)

化简整理得到

(9)

将所得关系式带入原规划，可得原问题的对偶规划

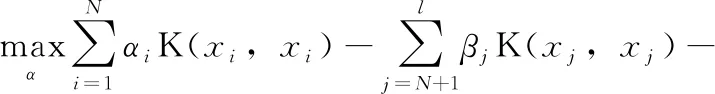
(10)

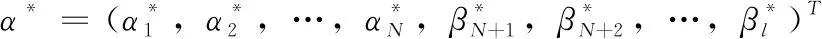
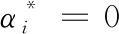
(11)

给定测试样本z，SHM采用如下符号函数来判断样本的类别

(12)

1.3 算法复杂度分析

选取经典的SVM和SVDC算法，对比分析SHM算法的复杂度。不妨假设训练样本个数为l。SVM在训练时需要输入两类样本，所需时间和空间复杂度分为o(l2)和o(l3)。SVDC仅采集一类目标类样本信息，求取这类样本的最小包围超球，将落入描述边界内部和外部的样本分别定义为正类和负类。为了方便分析，不妨假定正负类样本个数相同，则参与训练的目标样本个数为l/2，SVDC需要的时间和空间复杂度分别为o(l2/4)和o(l3/8)。SHM采集目标类样本构造一个超球面分类机，时间和空间复杂度与SVDC相当；但是在约束条件中加入对非目标类样本的限制条件，从而超球半径的计算式(11)和决策准则(12)，完全不同于SVDC的计算式(4)和决策准则(5)。由于SVDC和SHM需要采集的数据数目较少，从而大大降低了存储空间；同时这两类算法具有较少的支持向量数目，从而降低了测试阶段所需的计算量和运算时间。

2 仿真实验

为验证SHM的算法性能，生成正态分布数据集，并选取部分规模不同的UCI数据集展开实验。所有算法采用MATLAB7.01编写程序，并在P4CPU，3.06 GHz，1 GB的PC机上模拟实现。

首先，对正态分布数据集验证SHM的有效性。产生正负类数目均等的样本集，并依次增加样本规模。随机互换3%的类别指标，选取80%的样本参与训练，其余参与测试。SHM将正类样本当作目标类，采用线性核函数，并取10次随机抽取实验的平均结果。为方便计算，SHM取C1=C2=C，表1列出在不同惩罚参数下的分类精度。

表1 SHM的分类精度

表1数据验证了SHM是一种有效的分类算法。SHM的分类精度较高，且随着惩罚参数和样本规模的变化而呈现一定规律性。SHM的分类精度先随惩罚参数的增加而增加，继续增加反而有小幅下降；SHM的分类精度随样本规模的增加先增加然后几乎保持不变。

其次，对比SHM与已有算法的分类表现。选取部分UCI数据，列出基本特征于表2；其中，正类指代数目较少的样本，负类指代数目较多的样本，比例是正类样本和负类样本的数目之比。

如果定义正负两类样本的数目之比为不平衡度，则表2中数据可以分为两部分：不平衡度较低的数据集，如Pima、Iris和Indian数据集；不平衡度较高的数据集，如Glass Ⅱ和Balance Ⅱ。

表2 数据集的基本特征

选取SVM、SSVM和SVDC作为比较对象，对比SHM的分类表现。所有算法采用十重交叉验证法选取最优参数，惩罚参数和径向基核参数的取值区域为lgC=[-2,-1,-0.5,0，0.5，1，2]和σ=[0.01,0.03,0.1,0.3,0.5,0.8,1]。支持向量机SVM和SSVM随机抽取总样本的50%参与训练，其余参与测试；支持向量数据描述算法SVDC和SHM将正类样本作为目标类进行训练，代入数目较多的负类样本进行测试。表3列出不同算法在最优参数下的分类性能。

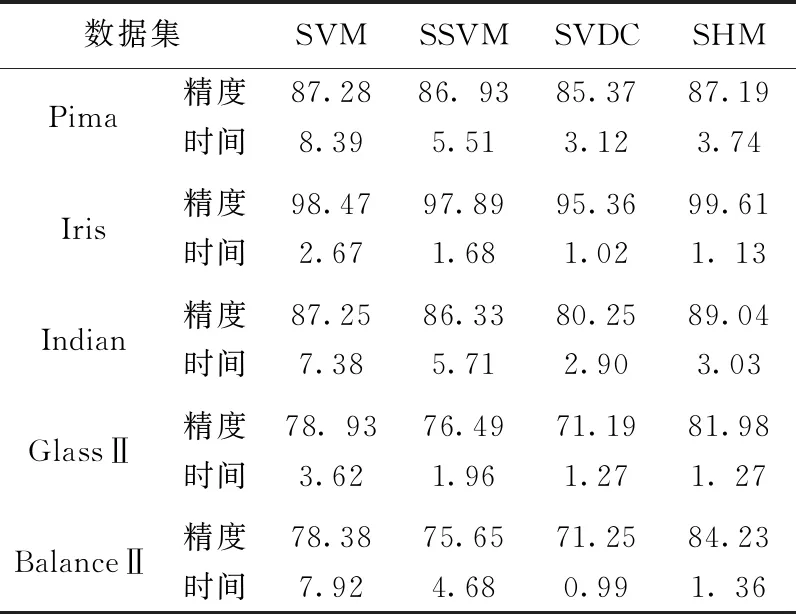
表3 不同算法的分类性能

在上述表3中，精度是训练集和测试集上的分类精度的平均值，时间是训练集和测试集上的运行时间的平均值。

观察表3数据得出结论：SHM在处理不平衡度较高的数据集时，能够显著提高SVM和SSVM的分类精度且缩减分类时间。SHM在处理任意不平衡度的数据集上，均能显著提高SVDC的分类精度，同时略微增加运行时间。

数据集Iris的不平衡度较低而Balance Ⅱ的不平衡度较高。在Iris数据集上，SHM将SVM和SSVM的分类精度分别提高1.14%和1.72%，而分类时间依次是两者的42.32%和67.26%。SHM将SVDC的分类精度提高4.25%，而分类时间仅多0.11 s。在数据集Balance Ⅱ上，SHM的有效性和优越性体现地更为明显，其分类精度分别比SVM和SSVM高5.85%和8.58%；而分类时间依次是两者的17.17%和29.06%。SHM将SVDC分类精度提高12.98%，而分类时间仅多0.37 s。

整体而言，SHM在分类精度和运行时间上具有良好表现：其分类精度与SVM相当，略高于SSVM和SVDC；其分类时间远远低于SVM，略低于SSVM而略高于SVDC。考虑到SHM可以提高SVDC的分类精度，增加的分类时间是值得的。

最后，阐明SHM的鲁棒性，也即分类精度随核参数变化而变化趋势。选取UCI中的Image数据集进行实验。该数据集规模较大，共含有2310个样本，其中正类样本1310个，负类样本1000个，故而在此数据集上的分类表现，可以视为算法的实际性能。实验中发现，不同算法随惩罚参数的变化趋势类似，故着重列出算法随径向基核参数的变化趋势。设定惩罚参数C=1，4种算法SHM、SVM、SSVM和SVDC的分类精度随径向基核参数σ的变化曲线列于图1。

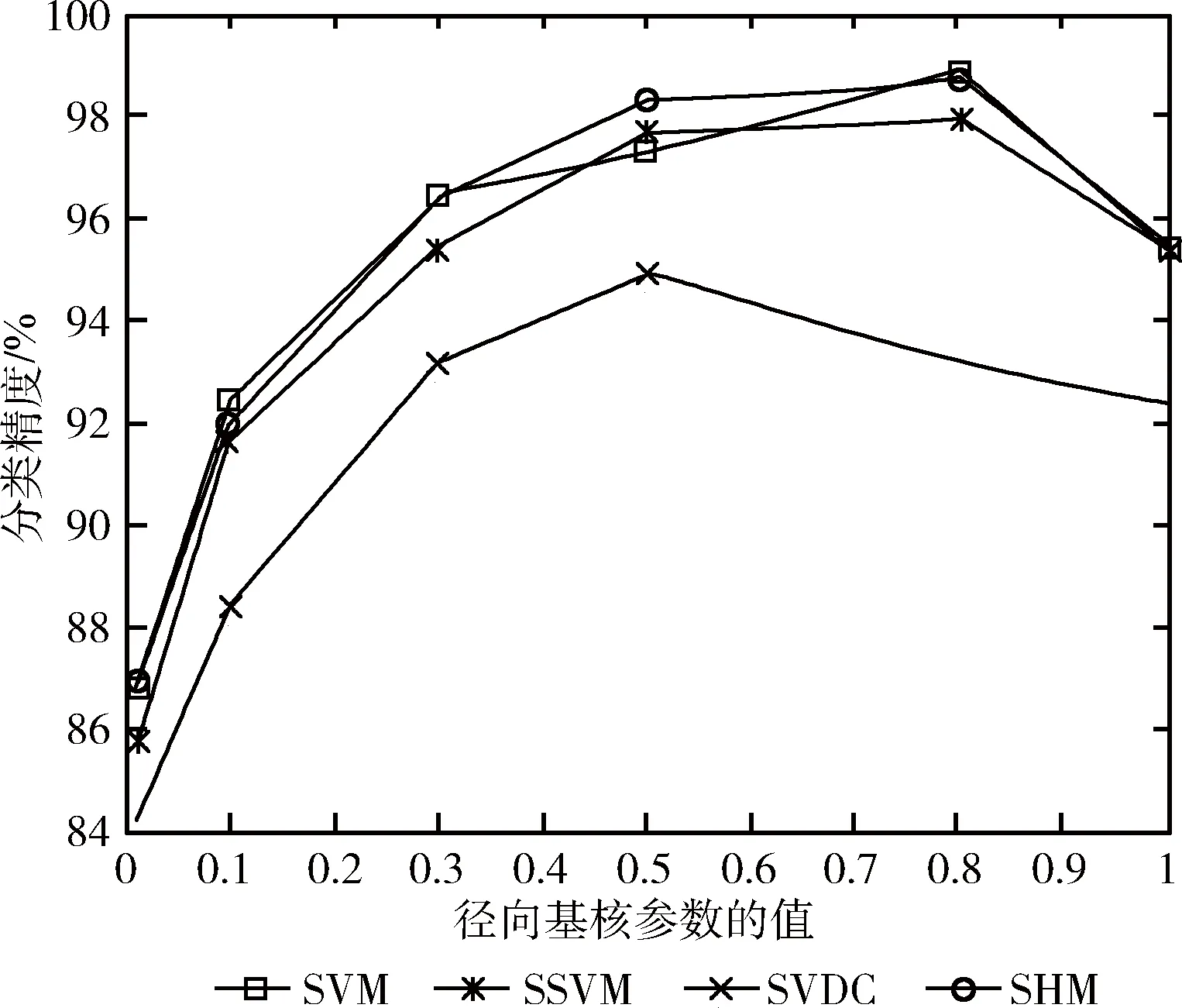
图1 分类精度随径向基核参数的变化曲线

观察图1曲线可以看出：SHM、SVM、SSVM和SVDC的分类精度均随径向基核参数的增加，出现先增加而后减少的变化趋势；但是4种算法的变化幅度并不相同。

整体而言，SHM和SVM的分类精度相当，两者均比SSVM的分类精度要高，且远远高于SVDC的分类精度。这验证了采用负类样本修正描述边界，可以显著提高SVDC的分类精度。

当核参数较小时，4种算法的分类精度并不高，这是因为“过拟合”造成对训练集过度学习，而一定程度降低了测试集上的分类性能；增大核参数，4种算法的分类精度先随之增加，进一步增大反而导致分类精度有一定程度的下降。其中，SHM、SVM和SSVM由于用到了两类样本的信息，分类精度随核参数变化的幅度并不明显；而SVDC仅利用一类样本的信息，分类精度随核参数变化增幅显著，也即算法的鲁棒性不高。

取训练集和测试集上运行时间的平均值作为分类时间，进一步验证SHM算法对比已有算法的优势。对上述径向基核参数的取值，给出取惩罚参数C=1时，不同算法的分类时间随径向基核参数的变化趋势，列出相应结果于图2。

图2 分类时间随径向基核参数的变化曲线

观察图2曲线可以看出：SHM的分类时间要远远低于SVM的分类时间，显著低于SSVM的分类时间。这是因为利用一类样本所需的计算和存储成本较低。SHM的分类时间略高于SVDC的分类时间。考虑到SHM提高了SVDC的分类精度，增加的分类时间是值得的。

3 结束语

闭合超球面机(sealed hyperplane machine，SHM)利用非目标类修正传统SVDD的超球形描述边界，并设计符号函数展开分类判别。SHM在不同规模的正态分布数据集上均保持了良好的分类精度；相较于已有算法，在UCI数据集上具有分类精度和分类时间上的显著优势，且这种优势在不平衡度较高的数据集上体现得更加明显。SHM具有较好的鲁棒性，大规模Image数据集上分类精度和分类时间随径向基核参数的变化曲线验证了这一点。本文的闭合超球面机针对二分类问题提出，如何拓宽SHM将其应用于多分类问题是进一步的研究方向。