重构约束的离散矩阵因式分解跨模态哈希

张万桢，刘同来，李志梅+

(1.桂林航天工业学院 实践教学部，广西 桂林 541004；2.广东工业大学 计算机学院，广东 广州510006；3.桂林电子科技大学 广西密码学与信息安全重点实验室，广西 桂林 541004)

0 引 言

跨模态检索(cross-modal retrieval)[1-5]是指用户能用任意一种媒体类型的数据进行检索，搜索引擎返回多种类型媒体数据的检索方式。其关键问题在于如何高效地解决多媒体数据之间存在的语义鸿沟[6-10]。为此，近年来国内外研究人员提出了多种跨模态哈希(cross-modal hashing)方法[11-15]。其中，基于协同矩阵因式分解(collective matrix factorization，CMF)的跨模态哈希方法[16-20]取得了令人瞩目的成果。CMF作为一种简单但有效的语义挖掘方法能够高效地学习多模态潜在语义，降低多模态数据间的语义鸿沟。然而这些基于CMF的方法仍然存在一些固有的缺点。首先，在学习潜在语义信息时，过去基于CMF的方法没有考虑在子空间映射过程中，部分冗余信息会随同多模态数据的主要语义信息一同嵌入，导致检索效率下降的问题。此外，许多方法使用松弛-量化的优化方式会导致哈希码产生大量的量化误差，降低检索性能。

为此，本文提出一种重构约束下的离散矩阵因式分解哈希方法(RDMFH)。RDMFH对不同模态使用CMF学习潜在公共语义矩阵的同时，对公共语义矩阵施加数据重构约束、离散约束与图约束。重构约束保证学习到的潜在语义冗余信息最小化；离散约束减小最终生成哈希码的量化误差；图约束使得最终生成的哈希码更具可区分性。基于以上3个约束，本文所提出的RDMFH不仅能充分发挥CMF学习多模态潜在语义信息的能力，同时克服了其鲁棒性不足，量化误差大的缺陷，使得哈希码具有更好的检索性能。

1 相关工作

根据是否使用数据自身的标签信息，已有的跨模态哈希方法可以分为有监督跨模态哈希方法和无监督跨模态哈希方法。

1.1 有监督跨模态哈希方法

有监督的跨模态哈希方法利用数据本身标注的真实标签信息探索异构多模态数据之间的相关性。通常的方法是在学习低维哈希码的同时嵌入标签的语义信息，增强哈希码的可区分性。典型的有监督跨模态哈希方法有最大语义相关哈希[21](semantic correlation maximization，SCM)、监督矩阵因式分解哈希、可扩展离散矩阵因式分解哈希、离散跨模态哈希[22](discrete cross-modal hashing，DCH)、离散潜在因子哈希[23](discrete latent factor hashing，DLFH)、鲁棒多视角哈希[24](robust multi-view hashing，RMVH)等。具体地，SCM利用正交约束序列哈希码，重构多模态数据的相关性矩阵，学习具有可区分性的哈希码；SMFH首先使用CMF学习多模态数据的潜在公共语义矩阵，然后对其施加图约束加强哈希码的可区分性；DCH使用线性分类器学习多模态数据的哈希码，并对所学习的哈希码进行标签回归增强哈希码的可区分性；DLFH使用潜在因子模型挖掘标签的语义信息，通过离散的优化方法得到最终哈希码；RMVH通过重构潜在语义到原始数据与同时保存多模态数据的模态间和模态内相似性，加强哈希码的鲁棒性和可区分性。

1.2 无监督跨模态哈希方法

无监督的跨模态哈希方法通过挖掘多模态数据本身的分布来学习数据的哈希码。通常的方法是将多模态数据原始的高维空间映射到低维的汉明空间，同时保存数据的原始分布。典型的无监督跨模态哈希方法有协同矩阵因式分解哈希(collective matrix factorization hashing，CMFH)、潜在语义稀疏哈希(latent semantic sparse hashing，LSSH)、混合相似哈希(fusion similarity hashing，FSH)、协同重构嵌入[25](collective reconstructive embedding，CRE)等。具体地说，CMFH首先使用CMF提取多模态数据的低维潜在语义，然后对其进行量化得到哈希码；LSSH对图像和文本分别使用CMF和稀疏编码学习多模态数据的低维潜在语义；FSH通过在多模态潜在语义中嵌入不同模态数据内部的结构相似性增加哈希码可区分性；CRE通过对多模态数据进行重构嵌入直接学习多模态离散语义。

2 方 法

为了加强CMF对哈希学习的鲁棒性，同时缓解松弛-量化优化方式对哈希学习的负面效果，提出了一种在重构约束下的离散矩阵因式分解哈希方法。与传统基于CMF的跨模态哈希方法相比，受鲁棒多视角哈希RMVH模型的启发，通过对多模态数据的潜在语义重构回原始数据，加强哈希学习的鲁棒性。同时，对多模态数据使用CMF直接学习离散潜在语义，减少以往使用松弛-量化优化方法产生的量化误差。为了简便表示，本文将集中于现实世界中最常见的两种媒体数据：图片与文本，下面将详细介绍本文方法的模型。

2.1 问题描述

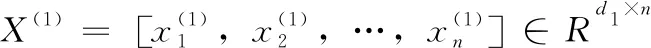
因此，本文提出重构约束的离散矩阵因式分解哈希方法的目的是学习数据库的统一哈希矩阵B与一组用于查询数据的映射函数：f1:X(1)→B和f2:X(2)→B。通过该组映射函数，用户的查询数据可以映射到低维的汉明空间，与数据库的哈希码B进行对比，然后返回与查询数据最相近的数据库样本。

2.2 重构约束的离散矩阵因式分解哈希

对于图片训练集X(1)与文本训练集X(2)，假设它们有共同的潜在语义V，根据矩阵因式分解模型可以表示为下式

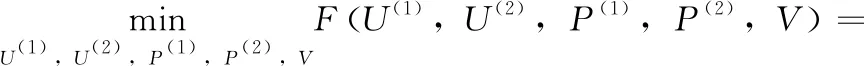
(1)

其中，U(1)∈Rd1×r和U(2)∈Rd2×r为因子矩阵，P(1)∈Rr×d1和P(2)∈Rr×d2分别为图片和文本的映射矩阵，α和β为超参数。式(1)中第一项和第二项分别为对图片集和文本集的矩阵因式分解，以学习它们共同的低维语义，第三项为线性回归项，以学习一组用于查询数据的映射矩阵。以往的基于CMF的多模态哈希方法，如CMFH、SMFH直接优化式(1)获得多模态潜在语义V和对应模态的映射矩阵P(1)和P(2)，然后使用符号函数直接量化矩阵V获得最终的哈希码B。

然而这些方法忽略了数据中的冗余信息，一张图片或一段文字中必然会存在与所描述事物不相关的冗余信息。简单地通过线性回归模型去学习映射矩阵P(1)和P(2)，会导致在泛化新样本时把原始数据中的冗余信息一起映射到潜在语义矩阵V中。在随后的量化过程中，冗余信息与核心语义信息一同被量化为哈希码，导致哈希码的可区分性下降，影响检索性能。此外，先优化式(1)再使用符号函数量化潜在语义矩阵V生成哈希码，会导致量化过程中产生大量的量化错误，也会影响最终生成哈希码的检索性能。

基于以上的讨论，受到RMVH的启发，本文提出一种新的重构约束的离散矩阵因式分解哈希，其公式化描述如下

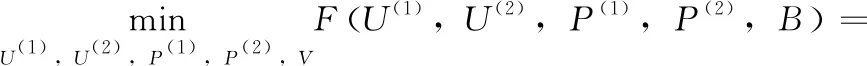
(2)

其中，Q(t)∈Rd(t)×r为重构矩阵，E(t)∈Rd(t)×n为重构误差矩阵。与式(1)不同的是，式(2)直接对多模态数据使用CMF学习离散潜在语义，通过优化式(2)，可以直接学习到离散的多模态数据的统一哈希码矩阵，避免松弛-量化步骤，减少了量化误差。同时，通过重构约束项X(t)=Q(t)P(t)X(t)+E(t)，将多模态数据分为纯净项Q(t)P(t)X(t)和冗余项E(t)，在学习多模态数据的离散潜在语义B时，只使用P(t)X(t)而排除了冗余信息项E(t)，增强哈希码的可区分性和映射矩阵的鲁棒性。同时，对E(t)施加L1范数约束是为了让重构误差尽可能小。此外，变量Q正交是为避免出现平凡解。

一般来说，希望同一类别样本的哈希码尽可能相似，而不同类别样本的哈希码尽可能不同。为了进一步增强所学习哈希码的可区分性，构造了一个图拉普拉斯矩阵以保存多模态数据的相似性，其公式化描述如下

(3)

其中，L∈Rn×n为相似矩阵S的拉普拉斯矩阵。把式(3)与式(2)结合，得到本文目标函数式如下

(4)

其中，γ为超参数。

2.3 优化算法

对于多变量的目标函数，通常的优化方法是交替迭代乘子法(ADMM)，优化其中一个变量时固定其它变量，然而式(4)中存在离散变量B，使得直接对式(4)使用ADMM进行优化变得非常困难，为此，我们采取一种灵活的替代优化方式[26]，通过引入一个辅助变量K，简化式(4)的优化过程。引入辅助变量K的目标函数式如下

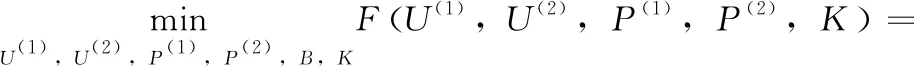
(5)

以往的方法已经证明，该替代方式可以很大程度上方便目标函数的优化，同时尽量不影响最终的优化结果。式(5)的增广拉格朗日函数如下

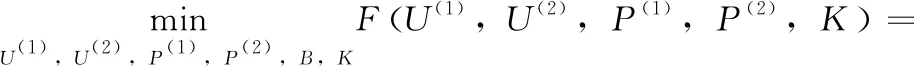
(6)

其中，Z(t)为增广拉格朗日乘子，μ为惩罚参数。通过该拉格朗日函数，将带约束优化变为无约束优化，进一步方便优化。对式(6)使用ADMM交替优化目标变量步骤如下。

步骤1 定除U(t)外的其它变量，式(6)对U(t)求偏导等于0解得

(7)

步骤2 定除K外的其它变量，式(6)对K求偏导等于0解得

A1K+KA2+A3=0

(8)

其中

可以通过使用Matlab直接求解该Sylvester方程求得K。

步骤3 定除P(t)外的其它变量，式(6)对P(t)求偏导为0解得

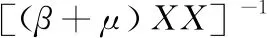
(9)

其中，D=βBX(t)+μQ(t)X(t)X(t)T-μQ(t)TE(t)X(t)T+Q(t)TZ(t)X(t)T。

步骤4 过解决下面方程，可求得变量Q(t)

(10)

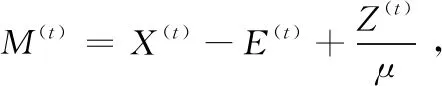
步骤5 定其它变量，令式(6)对B求偏导等于0再用符号函数量化得

(11)

步骤6 过下式更新变量E(t)

(12)

步骤7 过下式更新Z(t),μ

(13)

因此，通过迭代更新以上变量，直到达到设定的迭代次数来优化目标函数的各项参数，具体的优化过程见算法1。

算法1：本文的优化算法

输入：图像矩阵X(1)和文本矩阵X(2)，相似矩阵S，参数α，β，γ，α(1),α(2)，哈希码长r迭代次数T。

输出：映射矩阵P(1)和P(2)，哈希矩阵B。

(1)随机初始化所有变量矩阵；

(2)Repeat；

(3)用式(7)更新矩阵U(t)；

(4)用式(8)更新矩阵K；

(5)用式(9)更新矩阵P(t)；

(6)用式(10)更新矩阵Q(t)；

(7)用式(11)更新矩阵B；

(8)用式(12)更新E(t)；

(9)用式(13)更新Z(t)和μ；

(10)Until迭代次数。

2.4 时间复杂度分析

对于算法1，其计算的时间复杂度主要来自于求解Sylvester方程和SVD分解。下面详细列出算法1的各个步骤所需要的时间复杂度。在每一次迭代中：更新矩阵U(t)的时间复杂度为O(r3+r2d+rdn)；更新矩阵K的时间复杂度为O(n2)；更新矩阵P(t)的时间复杂度为O(rdn)；对一个d×r大小的矩阵进行SVD所需要的时间复杂度为O(dr2)，因此更新矩阵Q的时间复杂度为O(dr2+d2n)。一般来说有n>d>r，因此本文方法每一次迭代的时间复杂度约为O(n2+d2n+drn)。

3 实验与分析

本文在Wiki、NUS-WIDE和MirFlickr-25k这3个公开的基准数据集上进行实验验证与分析，并与最近的基于CMF的跨模态哈希方法进行对比，包括无监督的CMFH、LSSH、RFDH，和有监督的SMFH、SCARTCH对比。此外，为了进一步验证方法的有效性，还与非基于CMF的跨模态哈希方法RMVH、DCH进行对比。在两种常见的跨模态检索任务上进行对比和分析：①本检索图片；②片检索文本。

3.1 数据集

Wiki：Wiki数据集是从维基百科的文章中收集的图片-文本对，有2866组，共分为10大种类。每一张图片至少对应一段不少于70个单词的文段描述。每张图片被表示为128维的SIFT特征，而文本则由10维的主题特征所表达。该数据集共有10大类别，每一组图片-文本对对应其中一个类别。本文选取2173组样本作为训练集，其余的作为测试集。

NUS-WIDE：NUS-WIDE是一个真实的网络图像-文本数据集，它包含269 648张带有标签注释的图片，共有81个类别。本文选取其中10个数量最多的种类，共有186 577张带有注释的图片作为训练集。每张图像表示为500维的视觉特征，文本则表示为1000维的词袋向量，本文选取2000组图像文本对作为测试集，剩余的作为训练集。

MirFlickr-25k：MirFlickr-25k是从图片网站flickr上收集的图片-文本数据集，包含25 000组图片-文本对，共有24个类别。每张图片表示为150维的视觉特征，文本表示为1366维的词袋模型。本文选取2000组图像-文本对作为测试集，其余的作为训练集，数据见表1。

表1 实验数据集统计信息

值得注意的是，由于SMFH的计算复杂度太高，因此，为了方便实验，本次实验在NUS-WIDE数据集上仅采用5000个样本作为训练集训练对比。

3.2 实验设置

本文方法的参数设置如下：α控制不同模态数据对潜在语义影响的权重，一般设置为0.5；β设置为10；γ控制监督信息的权重，设置为100；α设置为0.001；迭代次数T设为10。此次实验的性能评估标准采用平均精度均值(mean average precision，MAP)。MAP反映模型的整体准确率，数值越大表示检索效果越好。为了避免随机初始化数据的干扰，所有的实验数值均重复10次取均值。实验环境为Intel(R) Core(TM) CPU I7-6700@4.0 GHz 32 GB RAM的服务器上运行，系统为WIN10。

3.3 实验结果与分析

表2与表3分别给出了本方法与对比方法在Wiki、NUS-WIDE和MirFlickr-25k这3个数据集上的两种跨模态务的MAP数值，哈希码长分别为16 bit、32 bit和64 bit。

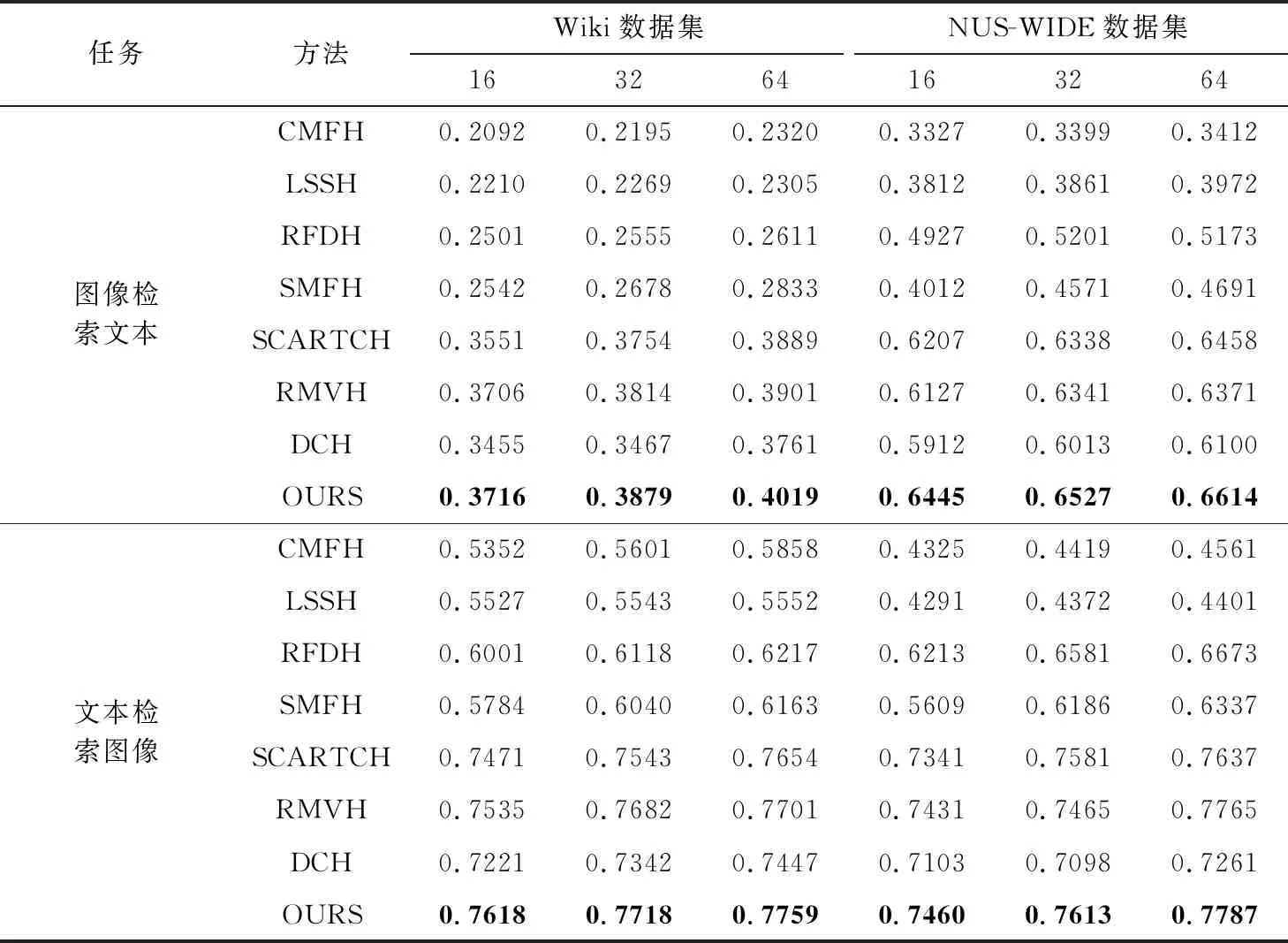
表2 在Wiki和NUS数据集上MAP值

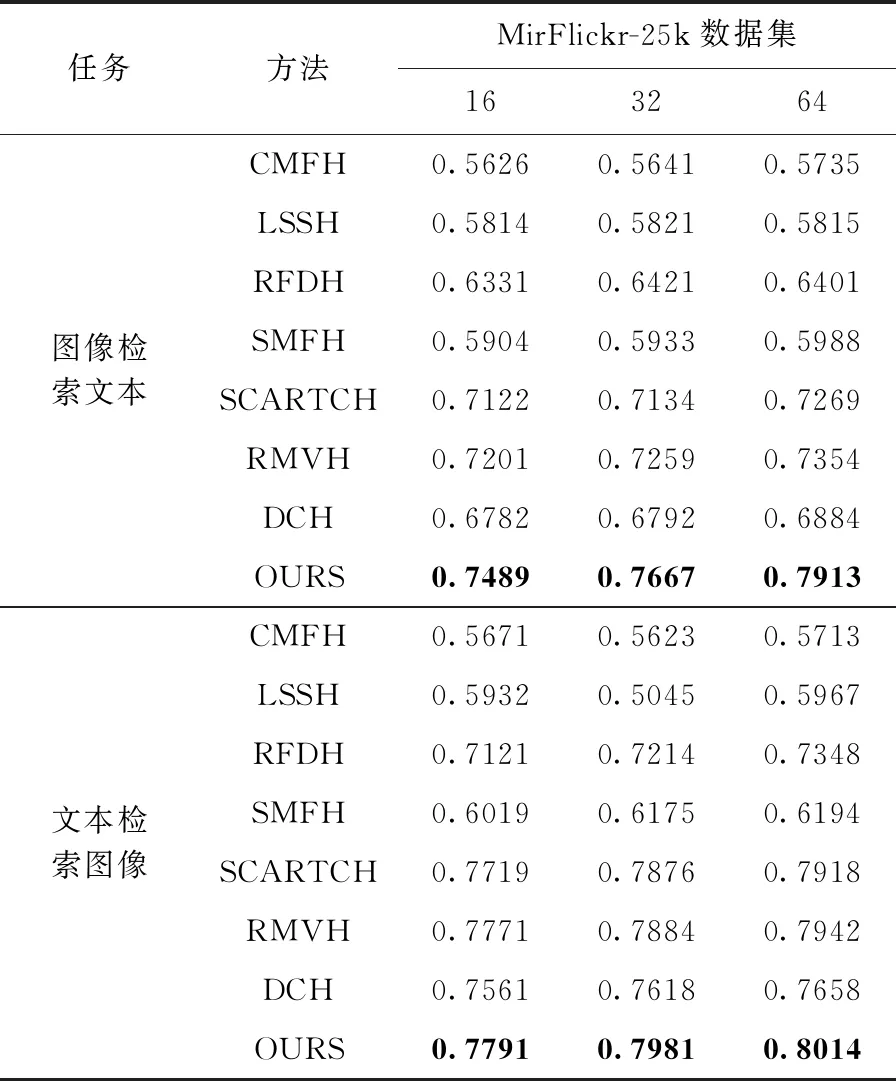
表3 在MirFlickr-25k数据集上MAP数值比较

表2、表3中最优的数值均用黑色加粗字体表示。

对于Wiki数据集，从表2的数据可以看出，本文的方法在不同哈希码长度下的MAP值优于所对比的方法，验证了本方法在跨模态检索任务中的有效性。值得注意的是，通过观察表2，可以发现大部分有监督跨模态哈希方法比无监督的跨模态哈希方法检索效果更好，这是因为有监督的方法通过嵌入真实的标签信息到哈希码中，可以大幅增加哈希码的判别力，因此有监督的方法通常比无监督的方法检索效果好。但是可以看到无监督的RFDH在文本检索图像任务中效果比有监督的SMFH好，这是因为RFDH是使用离散的优化方法优化哈希码，避免了松弛-量化过程造成的量化误差，而SMFH是使用松弛-量化的方法优化哈希码，所以无监督的RFDH效果比有监督的SMFH好。而本文方法也是采用离散的优化方法，因此检索效果优于非离散的方法。此外，通过表2还可以观察到，哈希码的码长越长，效果越好，这是因为哈希码的码长越长，哈希码所能保存的信息越多，因此检索效果越好。由于本文方法与RMVH均使用数据重构，使得哈希码能够尽可能少的受到冗余信息的干扰，哈希码所保存原始数据的主要信息比其它方法更多，因此检索的效果优于其它对比方法。

对于NUS-WIDE数据集，从表2的MAP数值比较中可以观察到，本文方法优于其它的方法，这与在Wiki数据集中的观察一致，再次验证了本文方法在跨模态检索任务中的有效性。此外，可以观察到，文本检索图片任务的MAP值比图片检索文本的MAP值普遍要高，这是因为文本所包含的信息比图片的信息要直观，能更好表达数据的核心语义。

对于MirFlickr-25k数据集，从表3的MAP数值对比中可以观察到，本文方法优于其它的对比方法，与Wiki、NUS数据集中的观察一致，进一步验证本文方法的有效性。

3.4 收敛分析

下面分析本文方法的收敛性，由于本文方法的优化方式是基于迭代的优化方式，因此优化算法的收敛性对模型的性能起到至关重要的作用。这里主要通过实验验证本文优化算法的收敛性。

图1为迭代次数与目标函数值的曲线图。从图1中可以观察到，本文方法在10次迭代左右就基本收敛，因此本文方法的整体计算成本并不高，可以有效地用于大规模的跨模态检索任务。

图1 目标函数迭代曲线

3.5 参数分析

下面分析参数对实验结果的影响，重点分析3个主要参数α，β，γ对实验的影响。由于实验过程中发现参数αt对本文方法实验影响很小，这里不作进一步分析。为了研究以上3个参数对实验结果的影响，在研究其中一个参数时，固定其它两个参数，固定参数的取值如上文所述，哈希码长定为16 bit，以MAP作为评价指标。

图2显示了各个参数在Wiki和NUS-WIDE数据集上的实验结果。从图2中观察到，当α取值为0.5时，本文方法在两个数据集中取得最优结果；参数β控制线性回归项对整个模型的影响，从图中可以看到，当β处于[1,50]时，模型的性能往上提升，当大于50时，模型性能下降，因此β的取值取中间值10为最佳；参数γ控制监督信息对模型性能的影响，从图中可以观察到，当γ的取值为100时，模型性能达到最佳，继续往上升模型性能下降，因此γ取值100。通过以上分析可知，本文方法参数能在一个较宽范围内取得不错的结果，对参数敏感性不强。

3.6 消融分析

为了进一步验证数据重构和离散约束对实验结果的影响，进行了以下3组消融对比实验。第一组对比实验为本文方法对比本文方法去除重构约束但保留离散约束项的结果，记为RDMFH-1；第二组对比实验为对比本文方法与本文方法去除离散约束但保留重构约束项的结果，记为RDMFH-2；第三组对比实验为对比本文方法与本文方法去除重构约束与离散约束的结果,记为RDMFH-3。实验在Wiki数据集上进行，采取MAP数值评估，实验结果见表4。表4中本文方法与RDMFH-1对比可以得出，重构约束项在检索性能上有约1%的提升，验证了重构约束项的有效性；对比本文方法与RDMFH-2可以看出，离散约束对哈希码的检索能力有较大的提升，在每一位哈希码上均有10%以上的MAP数值提升，说明离散约束能大幅度减少量化误差，提高哈希码的可区分性，增加检索能力。对比RDMFH-2与RDMFH-3可以观察到，在哈希码非离散的情况下，重构约束项仍然对哈希码有约1%的性能提升，再次验证重构项的有效性。

4 结束语

本文提出了一种重构约束的离散矩阵因式分解哈希方法。与以往的基于矩阵因式分解的哈希方法不同，考虑了异构多模态数据中普遍存在的冗余信息对学习公共语义空间的影响，通过添加数据重构约束，将由稀疏项建模的冗余信息与映射项建模的主要信息进行分离，增强所学习哈希码的鲁棒性与可区分性。同时直接学习离散的哈希码，避免松弛-量化造成的大量量化误差。大量的实验结果表明，本文方法优于其它基于矩阵因式分解的跨模态哈希方法。

图2 参数调优折线

表4 消融对比实验结果