水利工程控制测量中几种平面坐标系统建立方法的实践分析

苏秀永，邵火峰，吴 磊，沈 默，沈明安

(1.中国电建集团华东勘测设计研究院有限公司，浙江 杭州 310014；2.河南省振瑜测绘信息有限公司，河南 信阳 464000)

0 引 言

水利工程控制测量分为平面控制测量和高程控制测量。控制测量工作，在规划设计阶段，是为了测绘大比例尺地形图[1]；在施工阶段，是为了将图纸上的设计放样到实地上；在竣工后运营阶段，是为了监测工程建(构)筑物变形。各阶段建立的控制网分别称为测图控制网、施工控制网和变形监测网[2]；其中变形监测网多为施工控制网改造而成。在平面控制测量中，地表水平距离投影到参考(地球)椭球面上以及将参考椭球面上的长度投影到高斯平面上均会引起长度变形。国家统一坐标系统为了控制长度变形，虽然采用了分带投影，以满足中、小比例尺测图的基本要求，但长度变形依然存在；尤其是在高海拔和(或)远离中央子午线的地方存在的变形越大[3]。

因此，根据水利工程项目所在的地理位置和平均高程，合理确定测区中央子午线和投影基准面，建立工程平面坐标系统，使得由控制点坐标反算的边长与实地测量的水平距离在数值上尽可能相等。也就是要求地面测量的水平距离归算到参考椭球面上的高程改化值和参考椭球面的归算边长投影到高斯平面上的投影改正值之和限制在一定数值之内[3]，以保证大比例尺地形图测绘和放样精度和方便施工放样工作。从两项长度变形分析、推论，结合水利工程实例，讨论水利工程测量中几种平面坐标系建立的方法，并分析各种方法的特点、适用性。

1 两项长度变形分析

地球表面是个不规则的曲面，在地表测量的几何数据，一般是以椭球面为归算的参考基准面[4]。水利工程所用的地形图是平面图，需要将椭球面上的测量元素(边、角)投影成平面元素。高斯正形投影是一种等角投影，使平面图上的图形与椭球面上的相应图形保持相似，便于识图和用图，在控制点坐标归算及地形图测绘、制图中广泛应用[5]。归算、投影均会产生变形。

1.1 地表测量的水平距离归算到椭球面上的长度变形

地表测量的水平边长归算到椭球面上的长度变形△S1，计算公式[6]如下：

(1)

式中，S是地表测量的水平距离；Hm是测距边两端的平均高程(正常高)；hm是测区平均高程异常；H0是高程投影基准面高程(当高程投影基准面为参考椭球面时，H0=0)；RA是测距边所在法截线的曲率半径，为计算方便，实际工作中通常以地球平均曲率半径R来代替RA，同时忽略影响较小的hm，可将式(1)简化为:

(2)

R取6 371 km，测距边S取1 km，计算在不同高度的地表测距边，归算到椭球面上。测距边投影变形值△S1和相对变形值△S1/S如下所示(见表1)。

表1 不同高度的1 km测距边，归算到参考椭球面上投影变形值及相对变形值

从表1可见，△S1总是负值，表明将地表测量的水平边长归算到椭球面上，距离会变短[3]；|△S1|值与Hm成正比，随Hm增大而增大。

1.2 椭球面上的归算边长投影到高斯平面上的长度变形

参考椭球面上的归算边长投影到高斯平面上的长度变形△S2，计算公式[6]如下：

(3)

式中，S0=S+△S1，即S0是归算到椭球面上的边长；ym是测距边两端点横坐标平均值(测距边中点到中央子午线的距离，减去500 km)；Rm是参考椭球面上测距边中点的平均曲率半径；Δy是测距边两端点横坐标之差。为计算方便，实际工作中通常以地球平均曲率半径R来代替Rm，同时舍去微小量第二项，可将式(3)简化为:

(4)

R取6 371 km，归算边S0取1 km，计算不同位置(ym值不同)的归算边，投影到高斯平面上，投影变形值△S2和相对变形值△S2/S0如下所示(见表2)。

表2 不同位置的归算边，1 km长度投影变形值和相对变形值

1.3 两项长度综合变形

从表1、表2可以看出，当工程所在测区高程(大地高)大于159.28 m或测区中心平面位置离开中央子午线的东西方向距离(ym)大于45.05 km时，△S1、△S2值均超过规范[7]规定的25 mm/km，即△S1/S、△S2/S0值均大于规范[7]规定的1/40 000。两种长度变形之和△S=△S1+△S2，△S1、△S2符号一正一负，表明两者存在着抵偿的地带。

在实际工作中，综合考虑|△S|≤25 mm/km，即△S/S≤1/40 000。

(5)

为计算方便，实际工作中通常令S0=S，可将式(5)简化为:

(6)

2 坐标系的建立方法及其适用性分析

根据测区的地理位置和平均高程及长度综合变形值△S的大小具体情况，水利工程可分别采用以下几种方法建立平面直角坐标系[1_2]。其中用2.2、2.3、2.4、2.5方法建立的坐标系，称为地方坐标系、独立坐标系或工程坐标系，应与国家统一坐标系建立联系。

2.1 采用国家统一3°带高斯正形投影平面直角坐标系

由以上分析可知，当工程所在测区高程(大地高)不大于159.28 m且ym不大于45.05 km时，即长度综合变形值|△S|≤25 mm/km，可直接采用国家统一3°带高斯正形投影平面直角坐标系。这种坐标系测量成果能够“一测多用”。

但水利工程项目一般位于丘陵、山区，高程(大地高)多大于159.28 m，测区跨度几十公里到上百公里，综合变形值△S通常多达分米级。因此，这种坐标系，在水利工程项目中使用甚少。

2.2 采用“抵偿投影带”的高斯正形投影平面直角坐标系

这种坐标系仍以参考椭球面为高程投影基准面，选择1条子午线作为高斯投影的中央子午线，用高斯投影改正△S2抵偿高程投影改正△S1，使得△S→0。

高程投影基准面为参考椭球面时，H0=0，由(6)式可得：

(7)

式中，Hm取测区平均高程值，解算出“抵偿投影带”ym的值，以ym处的大地经度Lm作为“抵偿投影带”(也称任意带[7])的高斯投影中央子午线，一般取位至5′、10′。

如浙江省某水利工程，测区概况：大致呈东西走向，西高东低，测区平均高程Hm=100 m(19**国家高程基准)；中央子午线120°，3°带成果，最小横坐标y西=-90.5 km、最大横坐标y东=10.1 km，测区内边长综合变形不满足|△S|≤25 mm/km要求。

由式(7)可解得ym=±36.7 km，即在ym=-36.7 km(Lm=119°38′)处，△S1=-0.016 m，△S2=0.016 m，两项长度变形完全抵偿，△S=0。实际应用中，一般取Lm=119°40′，作为“抵偿投影带”的中央子午线。

式(7)是个理论推导公式，实际工作中，可使用更为简化的公式：ym=(y西+y东)/2，确定子午线Lm；也可直接选取测区内某条子午线或测区边缘子午线。经试算，测区内边长综合变形满足|△S|≤25 mm/km即可。

这种坐标系的成果与国家统一3°带成果关系紧密，坐标转换[8]方便。

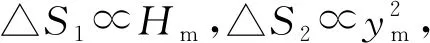
2.3 采用投影于“抵偿高程面”上的高斯正形投影3°带平面直角坐标系

这种坐标系，高斯投影仍沿用国家统一3°带中央子午线，但高程投影基准面由参考椭球面改为“抵偿高程面”，用高程投影改正△S1抵偿高斯投影改正△S2，使得△S→0。由(6)式可得：

(8)

式中，ym取测区中心横坐标值，解算出“抵偿高程面”H0的值，实际工作中，一般取位至整米或整十米。

如西藏某水电站，测区呈西北—东南走向，西高东低，中央子午线93°，测区3°带最小横坐标y西=-62.3 km、最大横坐标y东=-41.0 km，测区平均高程Hm=3 535 m(19**国家高程基准)，综合变形显然不满足|△S|≤25 mm/km 要求。

测区中心ym=(y西+y东)/2=(-63.2-41.0)/2 =-51.6 km，则由式(8)可解得H0=3 325.2 m，取整3 325 m；即选取H0=3 325 m的高程面作为控制网的高程投影基准面，高斯投影沿用中央子午线93°。测区中心ym=51.6 km 处综合变形趋向于0，测区东西两边缘处综合变形趋向于±25 mm/km。

实际工作中，一般先平差计算出一套国家统一3°带的控制网各点Pi坐标(xi，yi)，再将控制网缩放(一般是放大)到“抵偿高程面”上；也可在GPS控制网一点一方向约束平差时，“投影面高程”设置栏输入“抵偿高程面”H0的数值。

2.4 采用投影于“抵偿高程面”和“抵偿投影带”的高斯正形投影平面直角坐标系

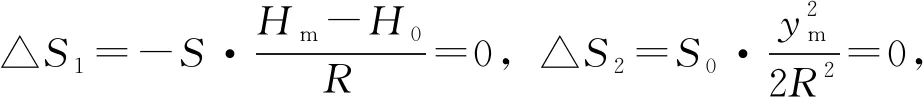
实际工作中，选择测区平均高程面或比其稍低一些的高程面为高程投影基准面；选择测区的中心线或其附近的某一子午线为高斯投影的中央子午线。

如云南省某水电站，测区南—北走向，呈Z字形状，测区横跨3°第33、34带(100°10′～100°40′)，北高南低，测区平均高程Hm=1 223 m(19**国家高程基准)，综合变形显然不满足|△S|≤25 mm/km要求。

该水利工程选取1 223 m为高程投影基准面、经度100°25′为高斯投影的中央子午线，建立测区平面直角坐标系。

这种坐标系内边长综合变形最小，坐标计算工作量相对较大，但适用性较广泛，特别适用于测区东西宽度较大、测区中心偏离3°带中央子午线较远和地面高程较大的水利工程项目。

2.5 采用投影于“抵偿高程面”的“一点一方向”平面直角坐标系

这种坐标系，选取测区内某一高程面为边长的高程投影基准面，不再考虑边长的高斯投影变形△S2，是以网中某固定点为起算点，以某一选定方向的坐标方位角为起算方位而建立的平面直角坐标系。

如浙江省某抽水蓄能电站施工控制网，该抽蓄电站上水库、下水库为全站仪边角网，上下水库之间采用GPS网连接(见图1)。全站仪所测的水平边长、GPS边长(由空间直角坐标计算的水平边长)，均以上下库平均高程457 m(19**国家高程基准)为高程投影基准面。边长不进行高斯投影，以下库中心点II06为起算点，以长边II06—II12(II12为上库控制点)为起算方位，“两网结合平差”，建立上下库统一平面基准，平面成果方便上、下库施工放样。II06、II12坐标采用国家3°带成果，使得施工测量控制网坐标系统与电站规划设计阶段的坐标系统非常接近。

图1 某抽水蓄能电站施工控制网示意

又如云南—四川某巨型水电站坝址施工测量控制网(见图2)，采用大坝中部高程680 m(19**国家高程基准)为高程投影基准面，边长不进行高斯投影，以BⅡ12为固定点，BⅡ12—BⅡ17为固定方位角的自由网。BⅡ12、BⅡ17坐标采用规划设计阶段成果，使得施工测量控制网坐标系统与电站规划设计阶段的坐标系统非常接近。

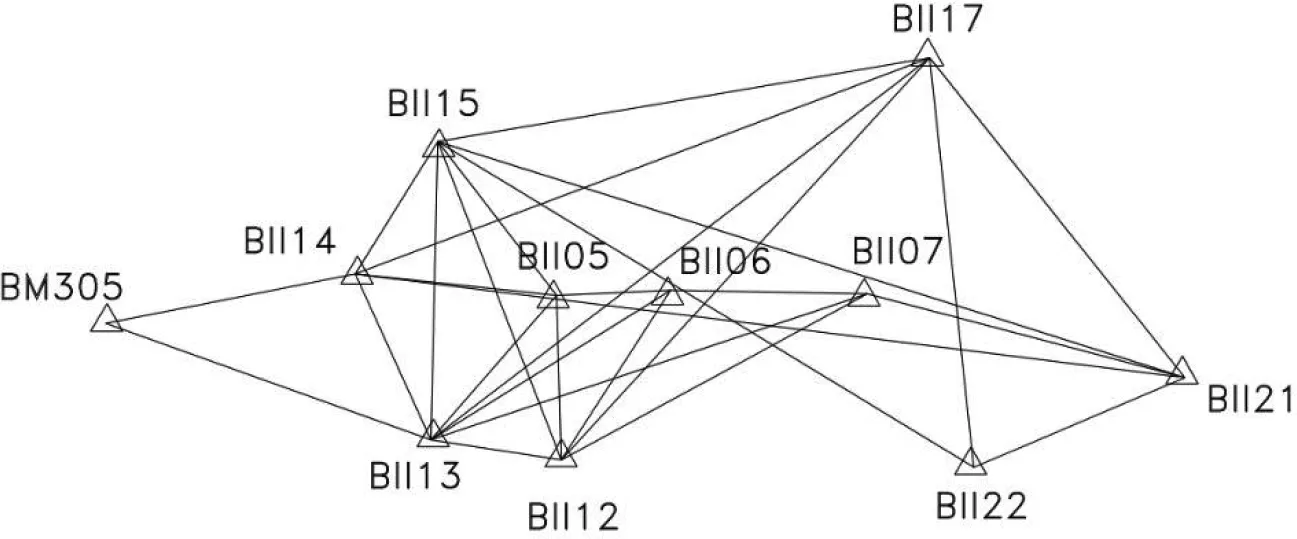
图2 某水电站坝址施工测量控制网示意

再如福建省某水电站坝址区变形监测网，由施工控制网改造而成，采用大坝顶部高程300 m(19**国家高程基准)为高程投影基准面，以坝右某固定点A为原点，以坝轴线为X轴，且指向左岸为正；以垂直于坝轴线为Y轴，且指向下游为正，采用全站仪边角网建立的独立坐标系统，在保证建网精度同时，也符合设计、施工的习惯。

这种坐标系适用于坝址、厂房等水电枢纽工程，范围小、整体精度要求高的施工控制网和变形监测网，以及抽水蓄能电站上、下库统一平面控制网。

3 结 语

平面坐标系统的建立主要考虑将长度综合变形控制在规范允许的范围之内，实质是根据测区地理位置和平均高程，对高程投影基准面和中央子午线位置的选择。实际工作中，应灵活选用上述几种方法，以确保水利工程项目大比例尺地形图测绘精度，在施工放样时方便使用控制点成果。

水利工程测区范围往往呈不规则状，测区内地势高低起伏较大，测区平均高程难以估算得十分准确。当使用计算和时，如果估算偏差较大，会导致测区内局部边长综合变形超限。因此，在实际工作中，应根据测区具体情况，认真估算，在确定之后，还应在测区范围内试算并调整。