全委托的公共可验证的外包数据库方案*

周搏洋,陈春雨,王 强,周福才

1(东北大学 软件学院,辽宁 沈阳 110169)

2(中国科学院 沈阳自动化研究所,辽宁 沈阳 110016)

随着信息技术的高速发展,智能手机等小型终端设备成为人们生活中不可或缺的一部分.然而,这些终端设备受限于较弱的计算和存储能力,无法承受庞大的数据量所带来的昂贵代价.伴随着云计算[1-3]的高速发展,这些弱计算能力的终端可以将数据外包给云服务提供商[4]管理,即用户将庞大的数据通过外包的形式让拥有强大计算能力的云服务器来存储和计算.通过这种将数据外包的方式,用户可以随时随地发出查询请求,云服务器则会根据不同的请求执行查询操作,并将结果返回给用户.因此,用户本地只需负责数据传输等简单操作即可,使得其持有轻量级设备即可执行查询操作.然而,由于用户丧失了对数据的直接控制[5],云服务器可能会伪造查询结果来减少响应时间和查询代价.这种资源租用的模式也带来了查询的安全性、正确性和隐私性等诸多问题.在这种情况下,如何使得用户能够检测和验证查询结果的完整性,成为了亟待解决的问题.

针对上述问题,Benabbas 等人于2011 年首次提出了可验证数据库(verifiable database,简称VDB)的概念[6],包括三方实体:数据拥有者、云服务器和用户.其中:数据拥有者持有数据库,并将其外包给云服务器存储;用户则可根据索引对数据库进行查询.由于具有可验证性,当用户对索引进行查询时,云服务器返回查询结果和一个能够验证结果完整性的证据.用户便可根据该证据来验证结果是否被篡改,即:得到查询结果的同时,又能验证其完整性.而其中需要满足的一个关键条件是:用户查询验证的开销要远远小于其在本地执行查询计算的开销,否则便失去了外包的意义.对于持有小型终端设备的数据拥有者而言,由于计算能力的限制,方案能实际应用的关键是,其使用轻量级设备在可接受的时间内能完成协议中的步骤.在可验证数据库方案中,数据拥有者的工作量主要由外包预处理阶段的开销构成,包括初始化和密钥生成算法.

近年来,国内外研究人员针对可验证数据库做了大量的研究[7-25],其中的很多方案在预处理阶段的开销超出了持有小型终端的数据拥有者的计算能力,以至于无法在现实中使用.如文献[18]利用向量承诺[26]的信息隐藏性和位置绑定性构建了一个可验证数据库方案,但由于向量承诺所需开销较大,数据拥有者在预处理阶段要 执行O(ℓ2)量级的指数运算才能实现初始化和密钥生成等操作,其中,ℓ为数据库中数据集的大小.当数据库很庞 大时,这样的开销对于轻量级的设备而言是不可接受的.为解决这一问题,文献[19]提出了一种分摊模型,将昂贵的预处理开销分摊到方案后面的查询步骤中,从而对每次查询而言“减小”其预处理阶段的开销.然而实际上,对数据拥有者而言,分摊的方式并没有减少其在整个方案中的工作量.因此,分摊模型依然不满足数据拥有者的关键要求.此外,在当前很多方案中,如文献[6,21],用户的验证过程需要私钥的参与,也就是说,只有持有私钥的用户才能验证查询结果的完整性.而在实际场景中,用户可能希望通过代理来验证查询结果,公共可验证则恰好满足此要求.在公共可验证的方案中,任何一个被数据拥有者授权,即持有验证密钥的用户均可以对外包数据库的查询结果进行验证.综上,在实际的不可信云环境中,如何在实现外包数据库完整性验证的前提下,又能够降低数据拥有者在预处理阶段的开销成为了关键,现有方案未能同时解决数据拥有者预处理开销大及公共可验证的问题.

针对上述要求,本文提出了一个全委托的公共可验证的外包数据库(publicly verifiable outsourced database with full delegation,简称PVDFD)模型,该模型具有以下两个特点.

1) 数据拥有者预处理开销小.利用可验证外包模幂运算,将预处理阶段大量的模幂运算委托给云服务器,使得数据拥有者与云服务器交互获得验证密钥的工作量小于自己生成验证密钥的工作量,同时保证验证密钥的保密性.这里的全委托是指除了将数据库外包给云服务器来检索外,还将预处理阶段生成验证密钥的部分运算交给云来完成;

2) 公共可验证.本方案支持公共可验证,即任何持有验证密钥的用户均可根据任意用户发送的查询请求及云服务器返回的结果和证据进行验证.

1 相关知识

本文所用符号见表1.

Table 1 Notations表1 符号说明

1.1 双线性映射

双线性映射[27-29]是指两个循环群之间相对应的线性映射关系.G1和G2均为p阶乘法循环群,g为群G1的生成元,定义2 个群上的双线性映射为e:G1×G1→G2,满足以下性质.

(1) 双线性:对于任意的a,b∈Zp和u,v∈G1,均满足e(ua,vb)=e(u,v)ab;

(3) 可计算性:对于任意的u,v∈G1,都存在有效的算法计算出e(u,v).

1.2 双线性Diffie-Hellman指数难题

双线性Diffie-Hellman 指数难题(bilinear diffie-hellman exponent,简称BDHE)[30]:G1和G2均为p阶乘法循环群,g,u为群G1的两个生成元,群上的双线性映射为e:G1×G1→G2.随机选择α∈Zp,给定一个元组(U0,U1,…,Un,Un+2,…,U2n),使得对于任意的i∈{0,…,n,n+2,…,2n}均满足.计算是困难的.

2 PVDFD 模型

本节主要介绍了全委托的公共可验证的外包数据库PVDFD 模型.首先给出了模型的架构及交互流程,然后给出了模型的形式化定义和安全性定义.

2.1 PVDFD模型架构

全委托的公共可验证的外包数据库模型PVDFD 中包含4 方实体,分别是可信第三方、数据拥有者、云服务器以及授权用户,其中,云服务器是不可信的,其他实体是可信的.模型架构如图1 所示.

Fig.1 Architecture of PVDFD图1 PVDFD 模型架构

可信第三方首先执行初始化算法生成公共参数,并将其分发给数据拥有者、授权的用户以及云服务器.数据拥有者在外包数据库之前,利用可信第三方生成的公共参数执行密钥生成算法生成密钥,包括数据库的查询密钥、验证密钥的计算密钥、验证密钥的恢复密钥和验证密钥的检索密钥,并将验证密钥的计算密钥发送给云服务器.云服务器执行验证密钥计算算法,返回编码后的验证密钥及相应的证据.数据拥有者利用验证密钥恢复算法验证,在验证通过的情况下完成验证密钥的恢复操作,将其发送给授权的用户,并将数据库的查询密钥发给云服务器.接着,授权的用户便可以向云服务器发送查询索引.由于云服务器是不可信的,其执行查询算法返回结果及证据,授权的用户执行验证算法实现验证操作,若算法输出1,则表示云服务器执行了正确的查询.由于持有验证密钥的用户均可对查询结果进行验证,因此该方案支持公共可验证.

注:本文中的数据库为NoSQL 类型,表示为DB={(i,vi)|i∈{0,…,n}},数据库中数据集大小为ℓ=n+1.

2.2 PVDFD的形式化定义

该模型可由概率多项式时间算法六元组PVDFD=(Setup,KeyGen,VKeval,VKrec,Query,Verify)表示,其中每项都代表一个多项式时间算法.6 个算法具体描述如下.

1)Setup(1λ)→pp:初始化算法.初始化算法由可信第三方执行,算法根据输入的安全参数λ生成公共参数pp,并发送给方案中的其他实体;

2)KeyGen(pp,DB)→(EKDB,EKpp,VKpp,RKpp):密钥生成算法.密钥生成算法由数据拥有者执行,算法输入数据库DB和公共参数pp,生成数据库的查询密钥EKDB、验证密钥的计算密钥EKpp、验证密钥的恢复密钥VKpp和验证密钥的检索密钥RKpp.其中,EKDB用来查询数据库,EKpp,VKpp,RKpp分别用来计算、恢复和检索数据库的验证密钥VKDB(数据库的验证密钥VKDB在下文验证密钥恢复算法VKrec中定义);

3)VKeval(pp,EKpp) →:验证密钥计算算法.验证密钥计算算法由云服务器执行,算法输入公共参数pp和验证密钥的计算密钥EKpp,输出编码后的数据库验证密钥和相关的证据;

5)Query(EKDB,x)→(y,πy):查询算法.查询算法由云服务器执行,算法输入数据库的查询密钥EKDB及授权 用户发来的查询索引x∈domain(DB),输出对应的查询结果和证据对(y,πy);

6)Verify(pp,VKDB,x,y,πy)→{0,1}:验证算法.验证算法由持有数据库验证密钥的用户执行,算法输入公共参数pp、验证密钥VKDB、查询索引x和云服务器返回的查询结果y的证据πy.验证通过输出1,否则 输出0.

2.3 PVDFD的正确性及安全性定义

2.3.1 正确性

PVDFD 方案的正确性,即:若模型中的每个算法都被正确地执行,则永远不会拒绝正确的结果.其形式化定义如下,其中,negl(λ)为关于安全参数λ的可忽略函数.

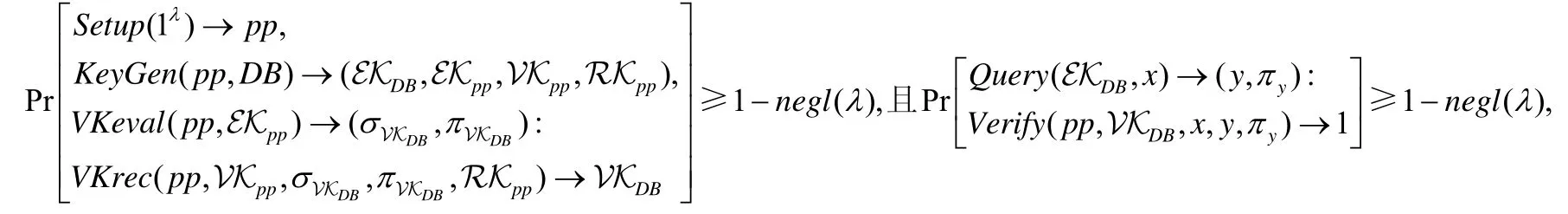
2.3.2 安全性

1) 验证密钥的机密性

验证密钥的机密性是针对不可信的云服务器而言的.简单来说,云服务器无法获取外包数据库的验证密钥.下面通过安全性实验来定义该模型中的验证密钥的机密性.定义敌手A(·)=(A0,A1),其中,A0,A1为两个概率多项 式时间模拟器,设计安全实验如下:

对于任意的λ∈N,定义敌手A在PVDFD 中的优势如下:

定义1.若,,则PVDFD 方案实现了验证密钥的机密性.其中,negl(λ)为可忽略函数.

2) 验证密钥的不可伪造性

验证密钥的不可伪造性是针对不可信的云服务器而言的,即,云服务器伪造一个验证密钥始终不能通过数 据拥有者的验证.下面通过安全性实验来定义该模型中的验证密钥的不可伪造性.定义敌手A(·)=(A0,A1,A2),其中,A0,A1,A2为3 个概率多项式时间模拟器,设计安全实验如下:

对于任意的λ∈N,定义敌手A在PVDFD 中的优势如下:

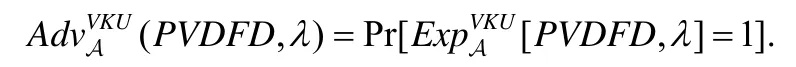
定义2.若,则PVDFD 方案实现了验证密钥的不可伪造性.其中,negl(λ)为可忽 略函数.

3) 查询结果的不可伪造性

查询结果的不可伪造性是针对不可信的云服务器而言的,即云服务器伪造一个查询结果和证据始终不能 通过授权用户的验证.下面通过安全性实验来定义该模型中的查询结果的不可伪造性.定义敌手A(·)=(A0,A1),其中,A0,A1为两个概率多项式时间模拟器,设计安全实验如下:

对于任意的λ∈N,定义敌手A在PVDFD 中的优势如下:

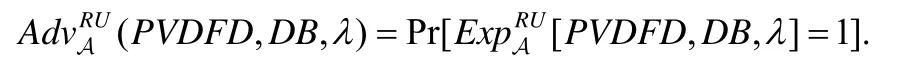
定义3.若(PVDFD,DB,λ) ≤negl(λ),则PVDFD 方案实现了结果的不可伪造性.其中,negl(λ)为可忽 略函数.

3 PVDFD 方案的描述

本节首先介绍了方案构建中用到的一个子协议MExp[31],然后详细介绍了PVDFD 方案中的各个算法,并给 出了正确性证明.由于本方案的安全性归约为BDHE 难题,在此难题中需要O(ℓ)量级的幂运算,因此数据拥有者 在预处理阶段要生成验证密钥所需的开销很大.而MExp协议为可验证的外包模幂运算协议,数据拥有者可以利用此协议,将这些幂运算外包给云服务器计算,同时又能验证结果的完整性.在此过程中需要注意的是:云服务器不能获取验证密钥的信息,否则,其可以伪造结果和证据而不被验证者察觉.

3.1 子协议:可验证外包模幂运算MExp

PVDFD 方案在预处理阶段的云服务器和数据拥有者交互生成验证密钥的过程中,用到了可验证外包模幂 运算协议MExp[31]作为子协议.为简单起见,令p为大素数,ui∈Zp作为底,ci∈Zp作为幂,其中,i∈{0,…,n}.MExp协 议由Ding 等人于2017 年提出,协议中存在两方实体:诚实的客户端和不可信的服务器.客户端希望将乘法模幂 计算外包给计算能力强但不可信的服务器来计算,而客户端能够验证结果的完整性.简单地提 取该协议中的系统模型,表示为以下3 个步骤,其中均省略modp操作.

1)ME.Setup(u0,…,un,c0,…,cn,p)→(ME.EK,ME.VK)

② 计算bi和t0h0,使其满足k2=k4(c0+c1+…+cn)-k0t0h0,其中,i∈{0,…,n};

③ 计算wi=ui/v0,其中,i∈{0,…,n},并生成逻辑划分如下:

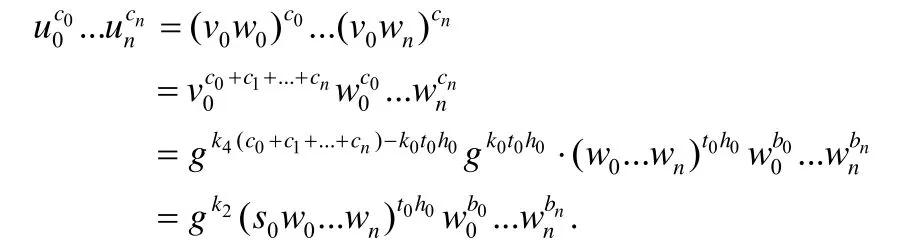
④ 选择随机数r∈Zp,计算,其中,i∈{0,…,n}.将进行逻辑划分如下:

⑤ 计算满足k3=k5r(c0+c1+…+cn)-k1t1h1和rci=+t1h1的bi′和t1h1,其中,i∈{0,…,n};

2)ME.Compute(MExp.EK)→{ME.σy,ME.πy}

此步骤由服务器生成编码后的结果ME.σy和证据ME.πy.具体如下.

① 将ME.EK分解为和;

② 对于i∈{0,…,n},计算和;

④ 返回结果和证据,分别为ME.σy=和ME.πy=.

3)ME.Verify(ME.VK,ME.σy,ME.πy)→{ME,y,⊥}

此步骤为客户端验证计算结果的正确性,具体如下.

① 将ME.VK分解为,ME.σy分解为 {,ME.πy分解为;

② 计算是否满足等式:

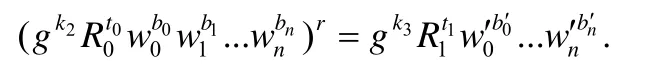
若不满足,则终止协议并输出⊥;否则,恢复计算结果ME.y=.

MExp协议有以下的性质.

1) 正确性:若服务器是诚实地遵循上述过程,协议可确保客户端总是可以输出ME.y;

2) 零知识性:协议可确保不遵守协议的恶意服务器无法获得任何秘密输入和输出(运算结果)的信息;

3) α-可检查性:协议确保检测到恶意服务器返回的错误结果的概率不小于α.

3.2 方案详细设计

本节首先详细介绍了PVDFD 方案中各个算法的具体构造,然后给出了正确性证明.下面分别进行描述.

1) 初始化算法.

该算法用于为方案中的所有实体生成公共参数.算法的主要步骤如下.

① 给定安全参数λ,可信第三方首先选择阶为p∈poly(λ)的两个群G1和G2满足双线性映射e:G1×G1→G2;

② 随机选取两个生成元g,u∈G1;

③ 令公共参数pp=(p,g,u,G1,G2,e)并发送给云服务器、数据拥有者和授权用户.

2) 密钥生成算法.

该算法用于生成方案所需密钥.算法的主要步骤如下.

① 数据库DB={(i,vi)|i∈{0,…,n}},其中,数据集大小为ℓ=n+1.数据拥有者先将数据库DB插值为多项式的形式,使得对于任意的i∈{0,…,n},均满足F(i)=vi.提取多项式F的系数集合为C={c0,c1,…,cn};

② 选择两个随机数γ,k∈Zp.令验证密钥的检索密钥RKpp=k,数据库的查询密钥EKDB=(C,γ);

③ 选择随机数α∈Zp作为伪随机函数(PRF)的密钥,并建立伪随机函数PRF(α,t)为:;

④ 记j为模幂操作的索引,对于∀j∈[2n+2]{n+1},执行MExp协议的初始化算法ME.Setup(u,αj+1,p)生成模幂计算求值密钥ME.EK[j]和验证密钥ME.VK[j].其中,u和αj+1分别为底和幂.当j=2n+2 时,执行算法ME.Setup(F,C,p)生成求值密钥ME.EK[j]和验证密钥ME.VK[j],其中,F={PRF(α,i)|i=0,1,…,n}为底;

⑤ 令验证密钥的恢复密钥VKpp={ME.VK[j]|0≤j≤2n+2∧j≠n+1}、计算密钥EKpp={ME.EK[j]|0≤j≤2n+2∧j≠n+1}.其中,

⑥ 最终,数据拥有者保持PRF密钥α,EKDB,VKpp和RKpp私有,并将EKpp发送给云服务器.值得注意的是:数 据拥有者在执行算法ME.Setup时只选择一次随机的六元组,在后面的操作中都使用该六元组.也就是说:对于所有的i∈[5]和j∈[2n+2]{n+1},均满足kj,i=k0,i.

3) 验证密钥计算算法.

该算法根据接收到的验证密钥的计算密钥来计算编码后的验证密钥.算法的主要步骤如下.

① 云服务器收到验证密钥的计算密钥EKpp后,将其分解为{ME.EK[j]|0≤j≤2n+2∧j≠n+1};

② 云服务器执行算法ME.Compute(ME.EK[j])生成编码后的结果ME.σy[j]和证据ME.πy[j];

4) 验证密钥恢复算法.

该算法用于对云服务器返回的结果进行验证,并恢复出数据库的验证密钥.算法的主要步骤如下.

② 执行算法ME.Verify(ME.VK[j],ME.σy[j],ME.πy[j]).

③ 当j∈[2n+2]{n+1}时,数据拥有者验证是否满足如下等式:

若不满足,则输出⊥并丢弃;否则,令:

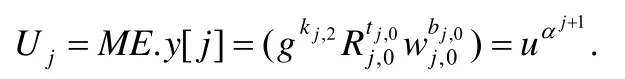
当j=2n+2 时,验证是否满足等式:

若不满足,则输出⊥并丢弃;否则,令:

④ 数据拥有者将{Uj}j∈[2n+2]{n+1}添加到数据库的查询密钥EKDB中,并将更新后的该值发送给云服务器.此时,EKDB={C,γ,{Uj}j∈[2n+2]{n+1}}.

⑤ 数据拥有者最终令VKDB={σDB,{Uj}j∈[2n+2]{n+1},RKpp,PRF(α,0)},并通过安全的信道发送给授权的用户.

5) 查询算法.

该算法用于查询数据库即执行多项式求值计算.算法的主要步骤如下.

① 当云服务器收到数据拥有者发来的EKDB以及授权用户发来的查询索引x后,首先将EKDB分解为{C,γ,{Uj}j∈[2n+2]{n+1}},并令X={1,x,x2,…,xn};

④ 将结果y和证据πy发回给授权的用户.

6) 验证算法.

该算法用于对云服务器返回的查询结果进行验证.算法的主要步骤如下.

① 授权用户收到结果y和证据πy后,首先将VKDB分解为{σDB,{Uj}j∈[2n+2]{n+1},RKpp,PRF(α,0)};

③ 验证以下等式是否成立:

若成立,则接受并输出1;否则,拒绝并输出0.

注:本方案亦可直接用于外包多项式的可验证计算,此时,多项式的更新效率为常量级.假设F为n阶的原外包多项式,F′为系数更新后的外包多项式,σF对应上文中的σDB,VKF对应上文中的VKDB表示外包多项式的验 证密钥,upd为更新信息.具体更新算法为

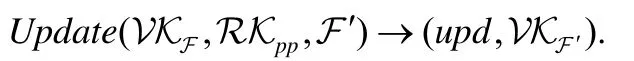
该算法在保证多项式的阶不变的情况下,可高效地对多项式的任意系数进行更新.算法的主要步骤如下.

① 假设更新的系数位置为i∈{0,…,n},令upd=.其中,ci为系数更改前的值,为更改后的值;

③ 外包多项式的用户将upd发送给云服务器,并将更新后的验证密钥VKF′重新发送给授权用户,即可实 现外包多项式的更新.

3.3 正确性证明

本节将基于公式(1)～公式(3)的正确性来证明整个方案的正确性.公式(1)、公式(2)可根据文献[31]来证明.而对于公式(3),其等式的左边(left-hand side,简称LHS)有:

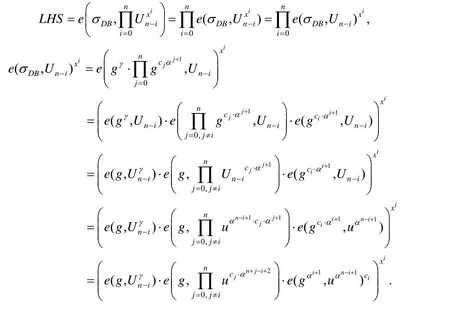
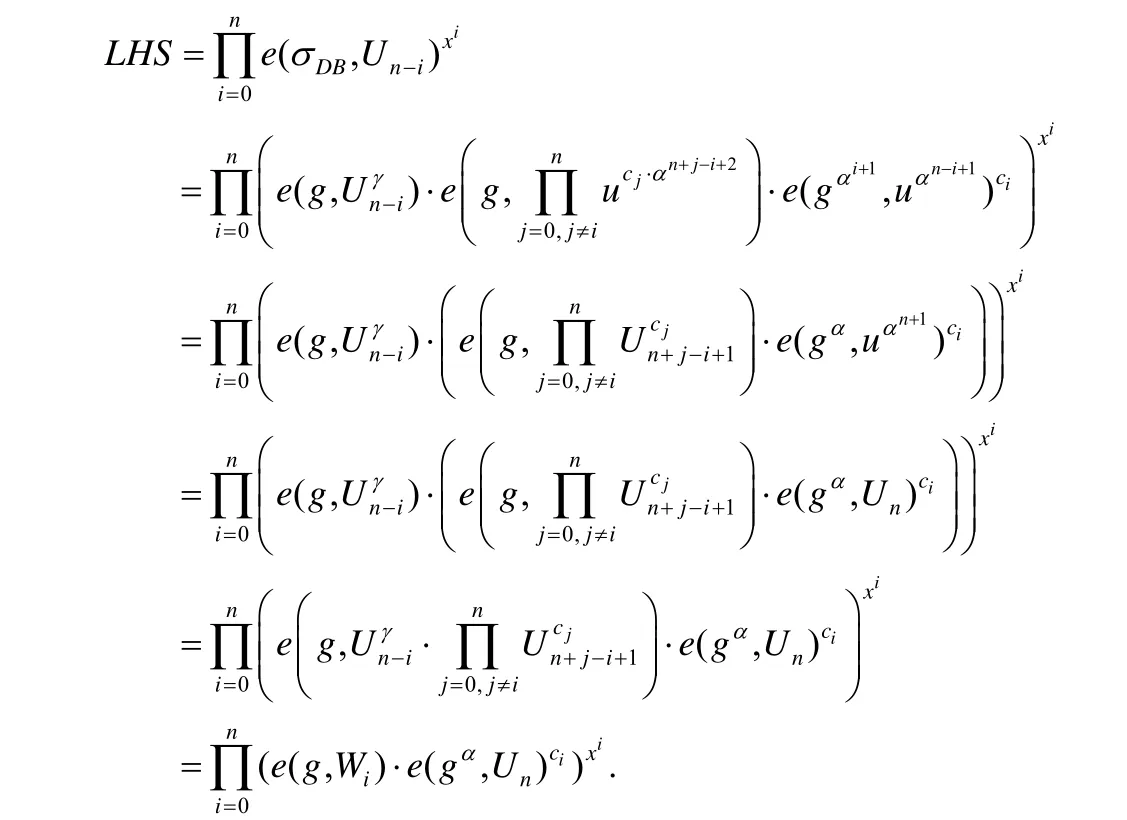
又由公式(3)等式的右边(right-hand side,简称RHS)可知:

即LHS=RHS,公式(3)成立.因此,若方案步骤都是正确执行,产生的结果都是未被篡改的,则结果和(y,πy)总能分别通过数据拥有者及授权用户的验证.

4 安全性证明

定理1.若存在一个概率多项式时间的敌手A,满足,则他可以创建一个有效的算法B来打破可验证外包模幂计算的零知识性.

证明:根据文献[31],若敌手A已知公共参数信息,且能够构建一个算法B区分计算结果和哪一个输入相关,即打破了可验证外包模幂计算的零知识性.

敌手A的挑战过程如下:已知公共参数为pp,敌手通过模拟器随机构造两个数据库的计算密钥和,并将其发送给挑战者;挑战者随机选择其中一个密钥,调用算法执行模幂运算,并将结果和证据返回给敌手;敌手收到结果和证据后,利用算法B猜测出b的值,即区分出计算结果 与哪一个计算请求相关.由此可知,敌手使用了有效的算法打破了可验证外包模幂计算的零知识性.

定理2.若存在一个概率多项式时间的敌手A,满足,则他可以创建一个有效的算法B来打破可验证外包模幂计算的α-可检查性.

证明:根据文献[31],若敌手A伪造了结果和证据,分别将其中的R0和R1替换为和,且满足,则伪造成功.敌手A利用伪造信息和真实的值可以构建一个算法B来打破可 验证外包模幂计算的α-可检查性.

具体构建过程如下:敌手A随机选择值R满足.令,根据等式:

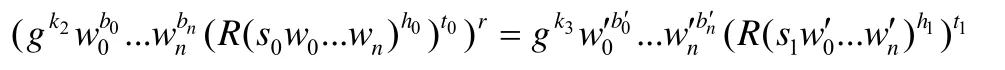
定理3.若存在一个概率多项式时间的敌手A,满足,则他可以创建一个有效的算法B来打破BDHE 难题.

证明:查询索引x*对应的值为y*,敌手A伪造了该值和证据,分别为.若伪造的值满足且=1,则伪造成功.敌手A利用伪造信息和真实的查询结果及证据可以构建一个算法B来打破BDHE 难题.

具体构建过程如下:令c=,即真值与伪造值的差值.由于验证通过,则一定满足以下等式:

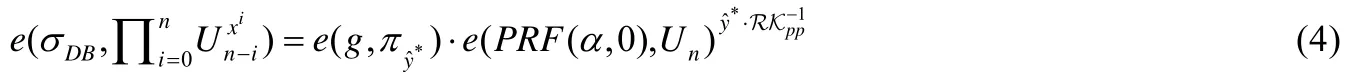
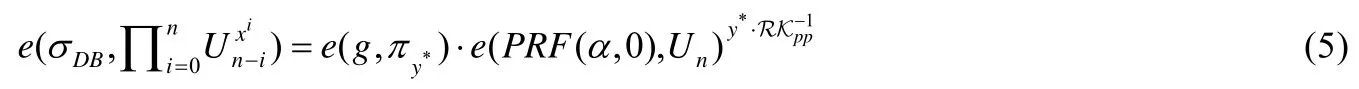
根据公式(4)和公式(5),可以推出:

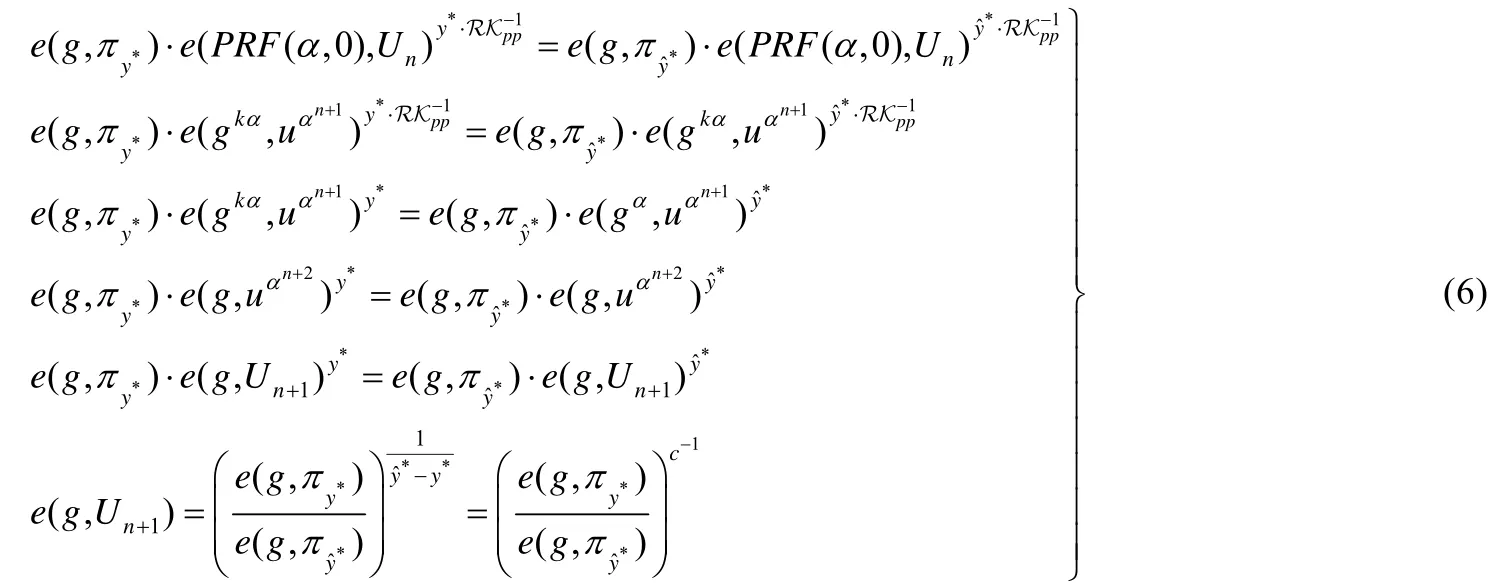
由公式(6)可知,敌手使用了有效的算法打破了BDHE 难题.

5 分 析

5.1 方案对比

本节将本方案PVDFD 与Miao 等人的方案[24](MVDB)、Chen 等人的方案[18](CVDB)、Benabbas 等人的方案[6](BVDB)、Backes 等人的方案[21](BFVDB)和Wang 等人的方案[23](WVDB)进行了功能上的对比分析.主要比较了方案是否需要较大的预处理开销、是否支持公共可验证和计算难题的假设.结果见表2.

Table 2 Comparison among six schemes表2 方案对比

从表2 中可以看出,MVDB 方案、CVDB 方案和BVDB 方案在预处理阶段均需要数据拥有者执行昂贵的计算.这对于持有小型终端的数据拥有者而言,代价过于昂贵.而BFVDB 方案和WVDB 方案虽不存在预处理开销大的问题,却不能实现公共可验证,BVDB 方案同样存在不支持公共可验证的问题.本文的PVDFD 方案通过采用将预处理开销委托给云计算的方式,不需要数据拥有者过大的预处理开销,且支持公共可验证.

5.2 复杂度分析

BVDB 方案、BFVDB 方案和WVDB 方案不能实现公共可验证,本文的PVDFD 方案在功能方面优于三者,因此在本节中不做对比.本节主要对比了本方案和CVDB 方案、MVDB 方案及不进行全委托计算的方案(without full delegation scheme)分别在预处理阶段、查询阶段和验证阶段的计算复杂度.其中,不进行全委托计算的方案是指将本方案中由云服务器和数据拥有者交互生成验证密钥的过程由数据拥有者独立完成,即数据拥有者独立计算验证密钥,而其他步骤不改变所形成的方案.由于插值操作、双线性映射和指数运算的计算开销较大,因此忽略其他的运算,仅对比3 种方案中的插值操作开销、双线性映射开销和指数运算开销,结果见表 3.在表3 中,ℓ,Interplt,Pairing,Exp分别代表数据库中的数据集大小、插值操作的开销、双线性映射的开销以及 指数运算的开销.

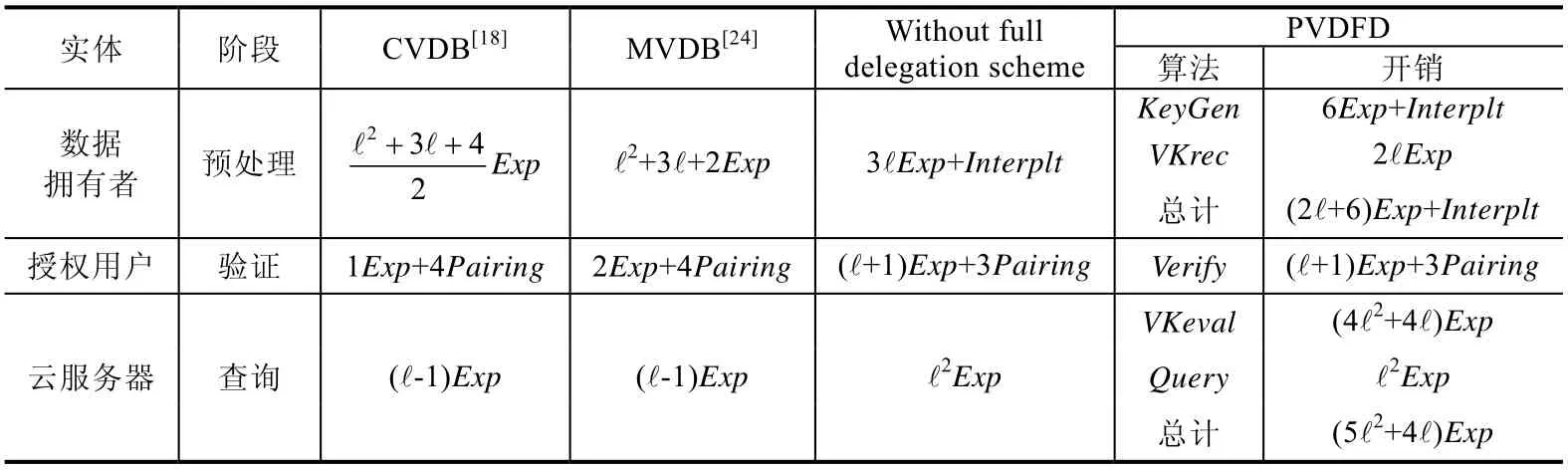
Table 3 Comparison of computation cost表3 计算复杂度对比

PVDFD 方案在预处理阶段,数据拥有者首先需要将数据库进行插值操作,并执行6 次指数运算生成Mexp协议中6 个隐藏的对;其次执行VKrec算法,执行2ℓ次指数运算以恢复验证密钥.因此,预处理阶段数据拥有者共需(2ℓ+6)次指数运算和一次插值操作.若不进行全委托计算,在本地执行全部的密钥生成操作则需要进行一次插值操作及3ℓ次指数运算.而CVDB 方案基于向量承诺实现,MVDB 方案基于向量承诺和布隆过滤器实现,二者在预处理阶段所需代价均为O(ℓ2).昂贵的平方量级的指数运算操作远远超出了数据拥有者的计算能力,尤其是 当数据库中的数据集较大时,其开销是不可接受的.显然,本文的PVDFD 方案在预处理阶段的工作量最低,证明了全委托方案的优越性.而在用户验证阶段,CVDB 方案和MVDB 方案的开销较小,为常量级;本方案和不进行全委托的方案的开销均要执行与数据库大小呈线性量级的指数运算,但线性量级的开销是用户可以接受的.CVDB 方案和MVDB 方案虽然在验证过程中开销较小,但在预处理阶段开销过大,使其仍无法实际应用.此外,由于云服务器可以认为是拥有海量计算资源的实体,拥有强大的计算能力.在PVDFD 方案中,云服务器执行的任务量最大,是对其强大计算能力的充分利用.CVDB 方案、MVDB 方案和不进行全委托计算的方案对云服务器的利用较小,不能使其充分发挥作用以减小数据拥有者本地的开销.

5.3 效率分析

本节通过实验对比分析了本方案与CVDB 方案、MVDB 方案及不进行全委托计算(without FD scheme,即第5.2 节所述数据拥有者独立计算验证密钥形成的方案)这3 种方案在预处理阶段、验证密钥生成过程、验证阶段和查询阶段的开销.实验采用PBC 库实现双线性群的初始化,采用NTL 库实现数据库的插值操作.运行实验程序的计算机配置为:Intel(R) Core(TM) i7-6700 CPU@3.40GHz 3.41GHz 主频的处理器和8GB 内存.

1) 比较本方案与CVDB 方案、MVDB 方案及不进行全委托计算的方案在预处理阶段的时间开销.

预处理阶段包括初始化操作和密钥生成操作.实验结果如图2 所示,其中,横坐标表示外包数据库中的数据集大小,纵坐标表示3 种方案在预处理阶段的执行时间.实验结果表明:本方案和不进行全委托计算的方案在预处理阶段时间开销较低;且当数据集越大时,两方案的时间开销越接近.这是由于数据集越大,数据库插值的时间则越长,指数运算的时间可以被忽略.而MVDB 方案和CVDB 方案的时间开销均远远高于二者,在数据集大小为10 000 时的开销甚至达到了约100 000s.其原因是MVDB 方案和CVDB 方案在预处理阶段需要过于昂贵的平方量级的指数运算操作,另两方案则只需线性量级的指数运算即可完成.当数据集较大时,MVDB 方案和CVDB 方案的时间开销是持有小型终端的数据拥有者所不能接受的.

2) 比较本方案和不进行全委托计算的方案生成验证密钥的时间开销.

实验结果如图3 所示,其中,横坐标表示外包数据库中的数据集大小,纵坐标表示两种方案生成验证密钥的执行时间.实验结果表明:两方案的执行时间几乎都与数据集大小呈线性关系,而本方案生成验证密钥所需时间 更低.由上文,要计算验证密钥中的σDB和{Uj},不进行全委托计算的方案需要进行3ℓ次指数运算,ℓ为数据库大小.而本方案执行验证密钥恢复算法,进行2ℓ次指数运算即可求得验证密钥.因此,本方案的开销更小,尤其当数 据集大小较大时,优势更加明显.

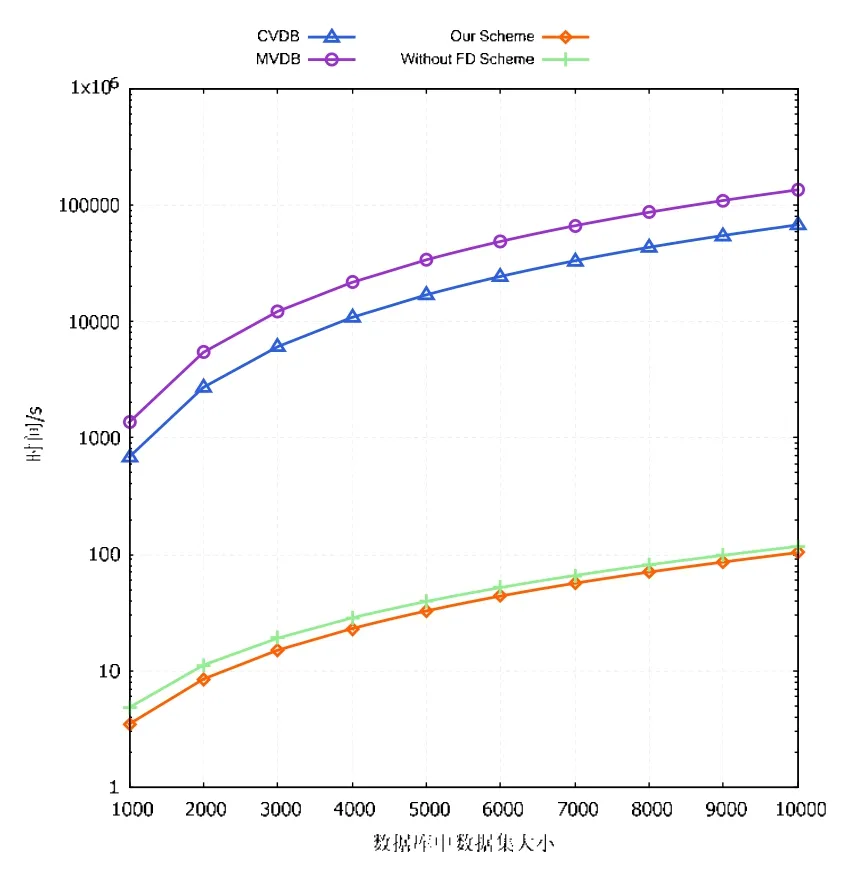
Fig.2 Comparison of time cost in pre phase图2 预处理阶段开销对比图

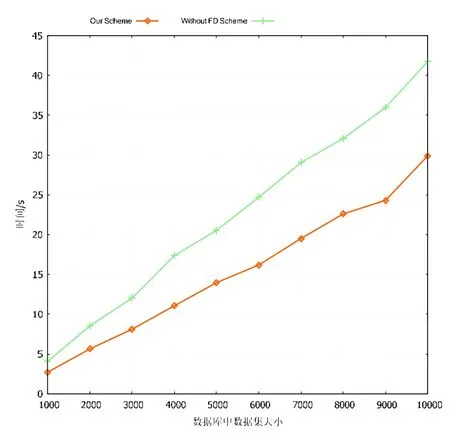
Fig.3 Comparison of time cost in VKEval phase图3 计算验证密钥的开销对比图

3) 比较本方案与CVDB 方案、MVDB 方案及不进行全委托计算的方案在验证阶段的时间开销.

实验结果如图4 所示,其中,横坐标表示外包数据库中的数据集大小,纵坐标表示3 种方案在用户验证阶段的执行时间.实验结果表明:随着数据集大小的增长,本方案和不进行全委托计算的方案所需的时间开销随之线性增长;而CVDB 方案和MVDB 方案中验证操作的时间开销则为常量级,独立于数据集的大小.这是由于本方案为了实现公共可验证性,使得用户执行线性量级的指数运算操作.但由图4 中可看出:当数据集大小为10 000时,时间开销约为14s,这对于用户而言是完全可以接受的.而CVDB 方案和MVDB 方案由于将大部分开销都放在预处理阶段执行,因此在验证阶段开销较小;然而其在预处理操作中过于昂贵的开销,使其难以实际应用.

4) 比较本方案与CVDB 方案、MVDB 方案及不进行全委托计算的方案在查询阶段的时间开销.

实验结果如图5 所示,横坐标表示外包数据库中的数据集大小,纵坐标表示3 种方案在云服务器查询阶段的执行时间.实验结果表明:CVDB 方案和MVDB 方案对云服务器的利用率最低,其次是不进行全委托计算的方案,而本方案对云服务器的利用率最高.这是由于CVDB 方案和MVDB 方案将大部分的开销放在了预处理阶段,数据拥有者执行昂贵的预处理操作,使得其查询和验证的开销较小.然而,云服务器的计算能力很强,数据拥有者的计算能力却是有限的,仅仅使用云服务器进行数据库的查询操作,是对其计算能力的浪费.此外,持有小型终端的数据拥有者执行如此昂贵的预处理开销是不现实的.因此,CVDB 和MVDB 两方案没有利用好云服务器的特性减小数据拥有者的开销.而不进行全委托的计算方案同样没有利用好云服务器的计算能力.本文把预处理阶段全委托给云服务器计算,合理地利用了云服务器强大的计算能力,减少了数据拥有者在预处理阶段的时间开销,虽然使得用户的验证开销略有增长,但该增长是在用户接受范围内的,这使得本方案更适于实际应用.

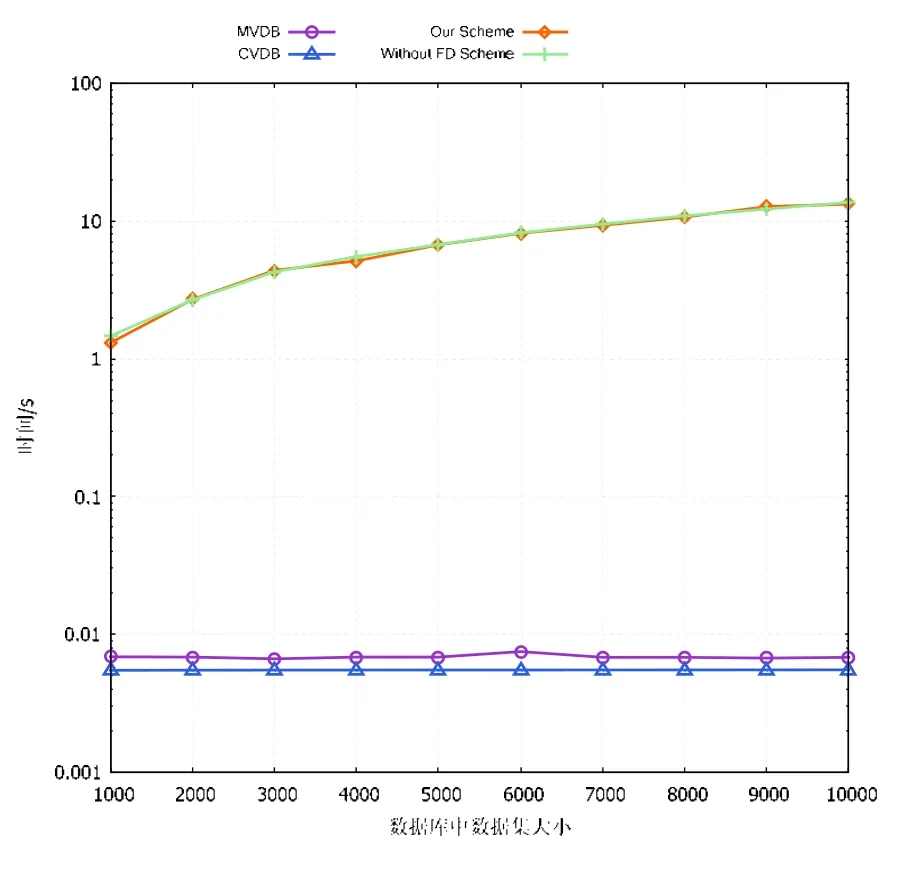
Fig.4 Comparison of time cost in verify phase图4 验证阶段开销对比图

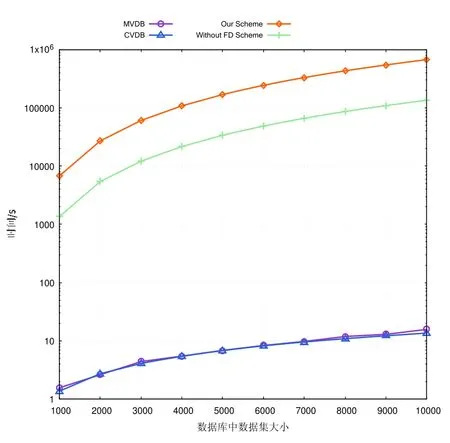
Fig.5 Comparison of time cost in query phase图5 查询阶段开销对比图

以上实验结果表明:PVDFD 方案很好地利用了云服务器具有强大计算能力的特性,使得数据拥有者在预处理操作的开销上有很大的优势;尤其当数据集较大时,优势更加明显.其原因是:在本方案中,数据拥有者将预处理操作全委托给云计算,而本地只需执行密钥生成操作及验证密钥恢复操作即可,两个操作的执行时间之和仍小于对比文献及不进行全委托计算的方案执行预处理操作的时间,因此本方案实用性更强.

6 总 结

本文提出了一个全委托的公共可验证的外包数据库方案PVDFD.通过将预处理阶段的工作量委托给云服务器计算,减少了数据拥有者的计算成本,且云无法获得任何与验证密钥相关的信息.此外,本方案支持公共可验证,使得任何持有验证密钥的授权用户均可向云服务器发出查询请求,并可以根据云服务器返回的计算结果和证据进行验证,实现了公共可验证.此外,本方案亦可用于外包多项式的可验证计算,且其更新的代价为常量级.本文还证明了PVDFD 方案的正确性和安全性.最后,通过理论和实验分析表明:PVDFD 方案解决了可验证数据库方案中,数据拥有者预处理阶段开销过高及不能公共可验证的问题.