长江上游10 m标志船水流阻力特性试验研究

刘 俊，胡 江，张 文，黄 纲

(1.重庆交通大学 水利水运工程教育部重点实验室，重庆 400074；2.重庆交通大学 国家内河航道整治工程 技术研究中心，重庆 400074；3.长江宜宾航道局， 宜宾 644002)

长江上游为大型山区河流，滩险众多，礁石林立，水流复杂，船舶航行时多借助于航标导航。天然情况下长江上游枯水期历时较长，水位比较稳定；而洪水期受暴雨径流影响，水位暴涨暴落，日变幅大。标志船随着水位变动受力状态发生改变，容易造成走锚，给船舶航行安全带来重大隐患。除去船型自身参数等内在因素外，标志船是否能正常工作的外界因素主要为水流条件，因此对其阻力特性的试验研究可以给标志船的布置工作提供指导。

国外对于浮标的研究起步较早且相关成果较丰富，但主要针对海洋浮标，标体一般为椭球形。早期贝托H. Q.[1]曾对海洋工程中浮标理论和实际问题进行过阐述，主要包括浮标力学、系留索力学和浮标实际问题等。而在国内长江上游河段中，标志船为较常见的一种助航标志，但关于标志船的研究不多，其中有部分学者根据三峡成库后航宽和航深相继增加等因素对三峡库区开展过研究，研究内容主要集中在标志船受力相关因素及航标配置等方面。杨斌[2-3]对三峡库区深水标志船进行受力分析，得出其系留所需缆索长度和深水设标的相关经验等；刘作飞[4]结合目前三峡库区航标配置和系留设施等情况，通过受力分析和维护实践经验对航标配置给出相应建议；冯飞[5]基于BP神经网络对长江航道标志船异动原因进行识别研究，提出适用于标志船异动原因识别相关算法，朱滔[6]针对长江上游漂浮物在标志船缆绳处造成堆积形成其失稳现象，提出一套检测及报警方案。以上研究成果基本采用理论分析，而关于现场试验与理论计算结合的研究相对较少，特别是标志船受力特性的定量研究。

本文针对长江上游河段10 m标志船，通过理论分析及现场试验，观测水深变动条件下标志船阻力特性。并将实测结果与理论计算结果进行对比分析，提出长江上游10 m标志船实际水流阻力计算式，研究成果对长江上游标志船的优化设置、维护长江航道安全畅通提供具有较好的依据。

1 标志船选型

在三峡库区中，以往主要有6.7 m以及10 m(分A、B型)规格钢质标志船[4]，其中B型10 m标志船为原长江上A型的改进型式。6.7 m标志船相对于10 m标志船而言，因浸水面积小，浮力就越小，但稳定性不如后者，一般适用流速较缓且流态良好的浅水区域河段；10 m标志船一般用于急流险滩等河段，包括流速、水深大且流态不稳定情况。自2017年起，长江航道局实施“擦亮行轮的眼睛”航标专项行动，提出对长江干线航标实施大型化，统一标志船尺寸的要求，全面淘汰6.7 m型标志船，因此叙泸段航道辖区现阶段基本全部采用B型10 m标志船，其中主要技术参数如表1所示。本次现场试验浮标选用B型10 m标志船，配套系缆锚石为长条形结构，标准重量约1 t，尺寸为1.3 m×0.7 m×0.4 m(长×宽×高)，标志船与锚石之间通过钢丝绳连接，长度约20 m。

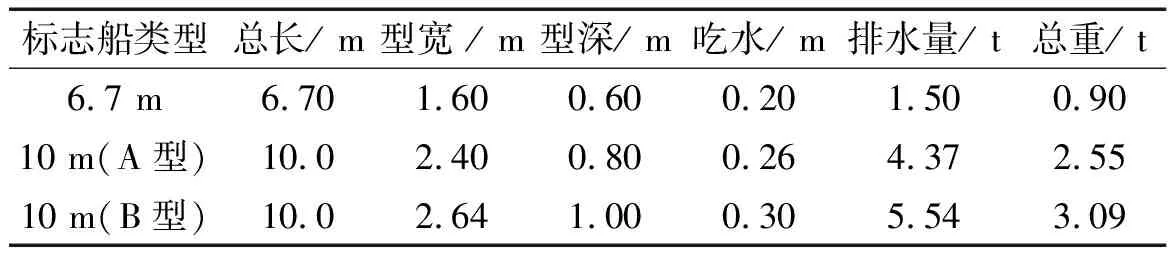
表1 不同标志船主要技术参数Tab.1 Main technical parameters of different lightship

2 标志船受力特性现场试验

图1 试验河段航道图Fig.1 Channel chart of tests reach

2.1 试验河段概况

试验选取长江上游叙泸河段共两块区域，所采用的试验航标共10处，其中包括红浮及白浮，见图1。龙船碛位于上游航道里程998 km，属铜鼓滩水道，为典型的弯曲河段，该滩段下段航槽弯曲狭窄、水流湍急，左岸鸭儿碛暗碛向河心延伸，右岸龙船碛平铺于江面占据大半河道，划定有船舶横驶区域，枯水期阻束水流形成急流滩，驶离横驶区域后航槽宽阔水流平缓。筲箕背滩位于上游航道里程1 004.5 km，属筲箕背水道，为过渡段浅滩，是川江上游著名的险滩之一，该滩上浅下险，上段航槽宽阔水流平稳，下段筲箕背与练家漕暗碛相对，枯水期阻束水流成急流滩，航槽下口弯曲狭窄。特别自金沙江向家坝枢纽蓄水运行以来，因上游日调节非恒定流作用，导致航道水位日变幅大，标志船随着水位变动对系泊角度造成影响，从而使得锚石受力状态发生改变，标志船设置可能需根据水位的变化需要予以调整，也给航道维护带来不利影响。

表2 标志船现场试验记录表Tab.2 Field tests records of lightship

综合以上分析，该试验河段具有航道弯曲狭窄、滩多水浅、水位涨落频繁和变幅大等特征，河床组成主要为砂卵石，基本保持稳定，水面平均比降约0.25‰。该河段水流流速在2.0 m/s以上，枯期流量约2 000 m/s3时滩上流速大部分约为3.0 m/s，个别滩险达4.0 m/s以上[7]，船舶航行困难需要及时避让滩险，因此标志船成为重要的助航设施。而标志船容易发生走锚，因此有必要进行其水流阻力特性的研究。

2.2 现场试验布置

为观测10 m标志船的阻力数值，试验选用5 t测力计、LS1206B型便携式流速流量仪及HY1600测深仪等仪器。试验开展于9月上旬，属于汛期，江面风速不大，天气晴朗。现场试验步骤：(1)测量人员采用5 t测力计连接标志船，位于江面上浮动；(2)当保持相对稳定时，测量人员位于标志船中部将流速仪垂直放入水面中保持1 min后，读取仪器表中的流速，利用测深仪读取测量位置的水深及无线手持仪读取测力计读数，本实验将测力计读数近似为标志船实际水流阻力数值；(3)依次选择10块不同区域，重复上述步骤，测取结果见表2。

3 现有标志船阻力计算式适应性分析

图2 理想状态下标志船受力图Fig.2 Stress analysis diagram of lightship

水中的标志船，与航行中的船舶相似，理想状态下主要受水流阻力、缆绳拉力、重力垂直分量和重力水平分量以及浮力的作用，见图2。其中又把重力水平分量称为坡降阻力，即船舶航行时克服与航向相反的船舶自重分力。关于标志船水流阻力的计算，本文根据船舶阻力的成因按照弗劳德阻力及产生阻力的物理现象进行分类，对应整理出理论公式和经验公式，而坡降阻力计算则是一个纯力学概念。

3.1 标志船阻力计算的理论公式

3.1.1 水流阻力

理论公式根据弗劳德阻力分类法将水流阻力分为摩擦阻力与剩余阻力两部分，通过理论分析结合船模试验，并针对川江水流特点和船型情况进行相关调整，得出川江驳船水流阻力表达式[8-11]，本文将标志船类似驳船分析考虑，则

(1)

式中：f1=k0[0.137+0.258/(2.68+Lw)]，k0=1+0.004 3(15-t)；As=Lw(C1T+δB)；Vs=(1.15.1.30)Vcp+Va；Am=βBT。

f1为驳船阻力系数；t为水温；As为船舶浸水面积，m2；Lw为船舶水线长度，m；C1为系数(驳船取2.0)；T为船舶吃水，m；δ为船舶方形系数，常取0.75～0.80；B为船舶型宽，m；Vs为船与水的相对速度，m/s；Vcp为船舶长度内纵向表面平均流速，m/s；Va为船舶上滩至少应保持的对岸流速，一般在0.3～0.5 m/s；ξ1为驳船剩余阻力系数，对川江一般取6.0；Am为船舶浸水部分舯剖面积，m2；β为船舶横断面系数，β=0.95～0.99。

3.1.2 坡降阻力

相比于水流阻力，坡降阻力为纯力学概念，一般采取下式计算

RJ=αWJ

(2)

式中：α为船队上滩时水面比降的修正系数，一般取α=1.1～1.2；W为船舶总排水量，kg；J为水面比降‰。

3.1.3 航行阻力

根据上述公式(1)和(2)可确定标志船航行阻力计算式

R=Rv+RJ

(3)

带入相关数值进行计算，其中驳船阻力系数f1=0.17，船舶浸水面积As=25.12 m2，剩余阻力系数ξ1=6，方形系数δ=0.8，船舶浸水部分舯剖面积Am=0.52 m2，见表3。理论公式虽然在我国山区航道整治中发挥了重要作用，但因公式本身结构不是很完善且只适用于部分河流，未能充分考虑不同河流实际特性，应根据实际情况建立适用于自身特点的计算公式，才能满足实际工程需求。

3.2 标志船阻力计算的经验公式

经验公式根据产生阻力的物理现象将水流阻力分为兴波阻力、摩擦阻力及粘压阻力讨论，相关阻力计算公式如下。

3.2.1 兴波阻力

(4)

式中：Rw为兴波阻力，N；Cw为兴波阻力系数；ρ为水的密度，kg/m3；V为水流流速，m/s；S为浮标湿表面积，m2，其中S=L(1.7T+δB)；L为标志船长度，m，其余符号同前。

目前关于船舶兴波阻力系数Cw数值计算，由于限制因素(波高、波长和周期等)过多且不易测取，主要依靠船模试验。本文拟通过《船舶原理》[12]中兴波阻力系数曲线图，选择较丰满船舶，观测曲线突变点，分段拟合得到相关表达式。

3.2.2 摩擦阻力

(5)

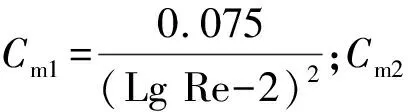
3.2.3 粘压阻力

(6)

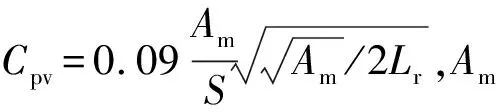
根据上述公式可确定标志船航行阻力经验计算式，带入相关数值进行计算，结果见表3。通过理论公式和经验公式航行阻力计算对比，可得两者增长趋势吻合较高。随着流速增加，航行阻力值越接近，造成该现象的原因可能为船舶航行时兴波阻力的干扰，针对低速船而言，兴波阻力在总阻力中所占比例很小，因此标志船阻力计算的经验公式也存在局限性，主要为波浪等因素的干扰。

表3 标志船理论公式和经验公式计算对比表Tab.3 Comparison of theoretical and empirical formulas for lightship

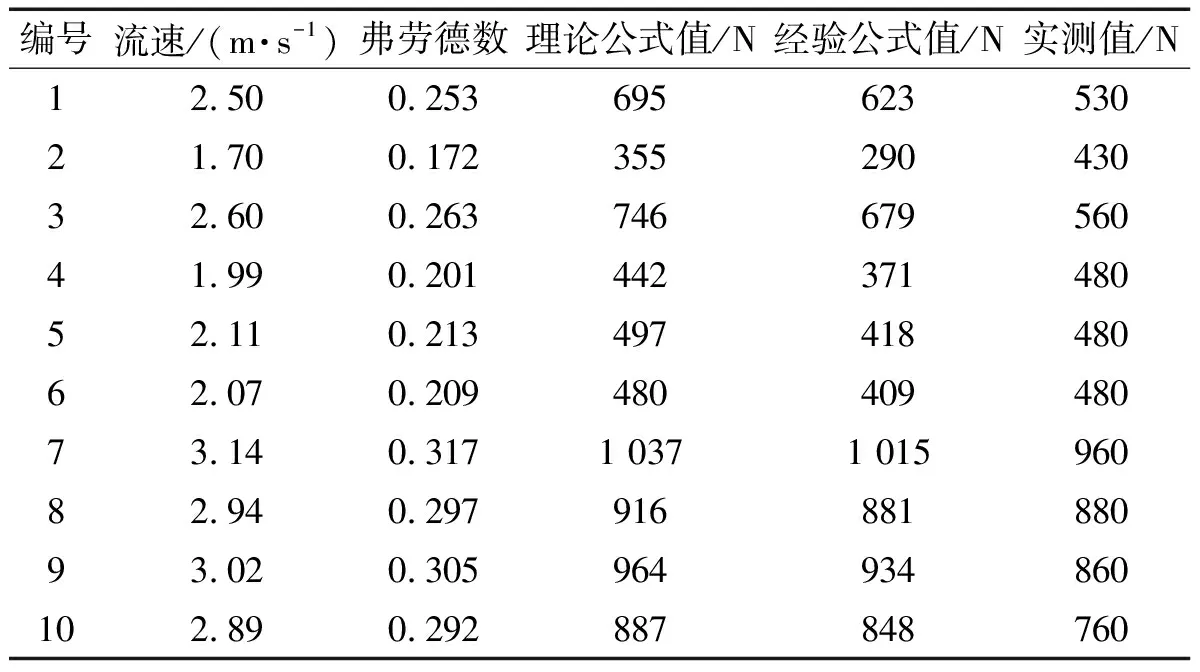
表4 实测值与理论计算值对比分析Tab.4 Comparative analysis of measured and calculated values

4 10 m标志船阻力特性分析

分析标志船阻力计算的理论及经验公式，发现与标志船航行阻力数值大小相关的因素，除船型自身参数之外，主要体现在水流流速和水面坡降两种参数。由公式(1)和(2)得，水流流速和阻力之间成指数关系，而水面比降则为线性关系。通过计算分析对比得两种公式计算得出的水流阻力在航行阻力中所占比例均很高，而且随流速增加，水流阻力所占比例越大，坡降阻力可以忽略不计。因此最能反映长江上游标志船受力特性的参数为水流流速。

根据标志船的理论水流阻力计算公式，将现场试验测取参数代入计算，理论计算与现场实测结果进行对比见表4，两种公式计算值和实测值之间存在一定的误差。由现场试验与理论分析计算结果对比分析图3可知，(1)现场试验与理论计算结果变化规律相似，即随着弗劳德数的增加标志船水流阻力而增大。其中理论分析的理论公式及经验公式计算曲线重合度高，增长趋势相对吻合；(2)实际水流条件下，相对于理论计算的线型变化趋势，标志船所受实际水流阻力受水流条件影响较大，整个关系曲线存在明显的分界点，而理论计算方法不能体现这种水流变化的差异性，其变化曲线基本一致，没有较大突变点，导致了其存在的局限性。

通过上述参数影响分析和前述驳船水流阻力计算公式(1)，针对长江上游10 m标志船，公式(1)可简化为

Rv=ξVm

(7)

(8)

式中：ξ和m为相关系数；V为水流流速,m/s；g为重力加速度，取9.8 m/s2；L为标志船长度,m。

根据船舶弗劳德数与航行阻力实测值绘制曲线，见图4，选择在Fn为0.25处进行分段拟合，可得公式(9) ，其中两个区间拟合的相关系数R2分别为0.973 6和0.971 9，拟合程度较高。

(9)

上述简化计算公式计算值与实测值对比见图5，除个别点存在偏差，其余各点均吻合较好，相关性较高，其中最大误差基本控制约±5%。综合以上分析，公式(9)较为符合长江上游10 m标志船的实际情况，可用于标志船的水流阻力计算。

5 结论及建议

(1)长江上游10 m标志船主要受水流阻力和坡降阻力影响，其中水流阻力占主导，坡降阻力计算时可忽略不计，而与水流阻力最相关的参数为水流流速；(2)长江上游10 m标志船水流阻力理论计算方法不能完全体现浮标水流变化的差异性，其变化曲线基本趋于一致。其实际水流阻力受水流条件影响，在Fn小于0.25时，阻力增长较缓慢；而Fn大于0.25时，阻力迅速增加。通过引入船型弗劳德数,并考虑水流流态影响，可得长江上游10 m标志船的水流阻力简化计算公式；(3)虽然本文给出了10 m标志船的水流阻力计算公式，但现场试验河段选择不多，研究成果适用范围有限，在成果运用过程中应注意河段的选取。