复杂流态下系泊船的水动力特性研究

张 博，姚慧岚，刘洪杰，刘 勇

(1.中国海洋大学 工程学院，青岛 266000；2.浙江省交通规划设计研究院有限公司，杭州 310000)

全球经济的快速发展，使得船舶逐渐向大型化以及专业化发展，港口工程建设也不断走向深海和远海。深海码头以及开敞式码头泊位处的水流条件十分复杂，如宝钢马迹山码头等[1]，具体表现为水流速度大、横向水流明显、水流方向沿水深变化等。系泊船在码头停泊或系泊作业时会受到严重影响，甚至出现断缆现象，威胁系泊船的泊稳安全以及作业效率。因此，有必要对复杂流态下系泊船的水动力特性进行研究，为大型船舶系泊方式优化、保证泊稳安全等提供一定的科学依据和参考。

Bomze基于一阶线性波理论和Froude-Krylov假设，发展了浮动刚体六个自由度的运动方程系统，考虑了作用在刚体上包括水动力、系泊力及龙卷风或水流引起的外力在内的作用力。Krishnankutty等[2]研究了船舶航行所产生的波浪和水流对系泊船的影响，他们首先将系泊船简化成抛物线截面，然后求解系泊船的运动方程，分析不同种类的系泊缆绳所受的作用力，并将其与已有试验和理论结果进行了对比。于洋等[3]对码头系泊船的水动力特性进行了研究，将船体处理为细长体，计算了二维船体剖面的附加质量，数值结果表明，在某些频率处，附加质量为负值。张福然等[4]通过理论分析、模型试验以及与国外计算公式的对比分析，给出了计算船舶水流力系数的经验公式和半经验公式。陈春升[5]采用物理模型试验方法对LNG船在不同风浪流组合作用下的船舶运动量、系缆力和撞击力进行了研究，结果表明：不规则波作用船舶运动量、系缆力和撞击力普遍大于规则波；45°斜浪的作用对船舶运动量、系缆力和撞击力的影响最大。杨宪章等[6]针对宁波舟山港马迹山矿石码头的较强潮流条件，开展了波流联合作用下的系泊船模型试验，研究了水流对系缆力的作用规律。李焱等[7]开展了系泊船物理模型试验，得到了不同水流条件下系泊船的运动响应和系缆力，给出满足系泊船系泊安全的水流强度限制值。邹志利等[8]研究了风、浪、流耦合作用下系泊船的运动响应、系缆力和护舷碰撞力，讨论了不同水位和不同风浪流夹角对系缆力和碰撞力的影响。陈中一等[9]研究了25万t油轮在不同潮汐和流速条件下的系缆力，指出首尾缆和倒缆是最主要的缆力，流速对系缆力影响很大，并提出了相应的系缆方式和安全措施。向溢等[10]进行了系泊船模型试验，发现系泊缆绳张力的大小与水流及波浪的大小、方向都存在密切关系，在规则波作用下，对缆绳张力大小的影响次序为：流向、波高、流速、波浪方向与风向、风速，其中风的作用一般要比水流和波浪小。

综上，国内外学者从不同角度研究了对系泊船的水动力特性和系缆力，考虑了风、浪、流等各种因素对系泊船的影响。但是，在更为复杂的码头水流条件下，例如大横向水流流速、水流流向沿深度变化等，有关系泊船水动力特性影响的研究较少。在这种复杂流态条件下，现有规范中的系缆方式可能无法保证大型系泊船的泊稳安全。因此，有必要对复杂流态条件下系泊船的水动力变化规律进行研究。在实际中系泊船运动响应过程十分复杂，在最佳系缆方式未知的情况下，为减少计算量和六自由度之间非线性耦合的影响，本文对系泊船力学模型进行简化，由于缆绳通过对船舶横荡、纵荡、艏摇运动的约束使船舶停靠在码头处，因此可以考虑采用约束船舶横荡、纵荡、艏摇的方法来近似替代缆绳的约束作用，从而获得横摇、纵摇和垂荡自由的系泊船简化模型，并以简化模型为研究对象，对复杂流态下系泊船的水动力特性进行研究。

本文采用计算流体力学(CFD，Computational Fluid Dynamics)方法，研究复杂流态条件下系泊船的水动力特性。基于STAR-CCM+平台，以KCS(集装箱船)系泊船简化力学模型为研究对象，采用VOF方法捕捉气-液两相流交界面，应用SIMPLE算法对压力和速度进行耦合求解，结合重叠网格方法，求解RANS方程和Realizablek-ε湍流模型。在不同流速(后文以弗劳德数Fr替代)、不同流向角(β)的常规流态条件以及流向沿水深变化的复杂流态条件下，针对船模的绕流场进行瞬态数值模拟，分析系泊船横向力系数、纵向力系数、艏摇力矩系数以及横摇、纵摇、垂荡的变化规律，研究结果可为复杂流态下大型系泊船的系缆优化布置等提供科学指导和参考依据。

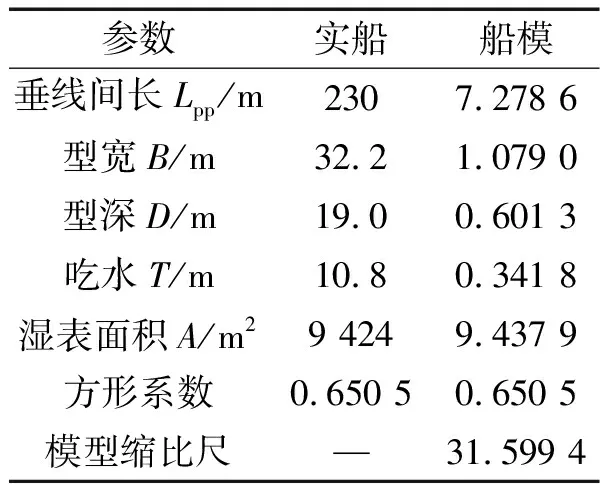
表1 KCS船型参数Tab.1 Ship type parameters of KCS

1 数值模拟方法

1.1 研究对象

本文以3 600TEU集装箱船KCS(KRISO Container Ship)模型为研究对象，该船在国际会议Tokyo 2015中有较多的水动力试验数据。KCS船型如图 1所示， 船型参数见表 1。

图1 KCS船几何模型Fig.1 Geometric model of KCS ship

1.2 控制方程

本文通过求解RANS方程对系泊船的粘性绕流场进行模拟，时均化后的连续性方程和动量方程如下

(1)

(2)

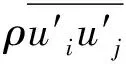
1.3 计算域及边界条件

根据ITTC(International Towing Tank Conference，国际拖曳水池会议)关于船舶水动力CFD应用的指南，进行计算域的设置(图 2)：入口距船艏1.5Lpp，出口距船尾2.5Lpp，左右边界距船中心线2.5Lpp，顶部据自由面1.5Lpp，底部距自由面2.5Lpp。边界条件设置为：入流面、左边界及上下边界均为速度入口边界，出流面和有边界为压力出口边界，船模表面为无滑移壁面。

1.4 网格划分

应用切割体网格技术对图2所示的计算域进行离散高质量的网格是数值计算的前提，本文对自由液面进行了网格加密，来捕捉自由面的变化，对系泊船近壁处的网格进行了三层加密，来保证计算结果的准确性及计算效率，如图3所示。

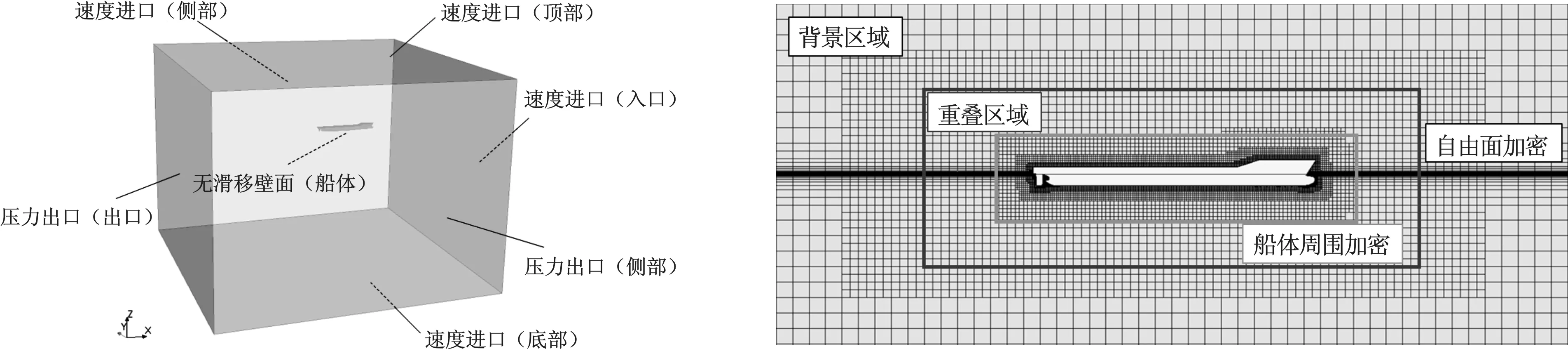
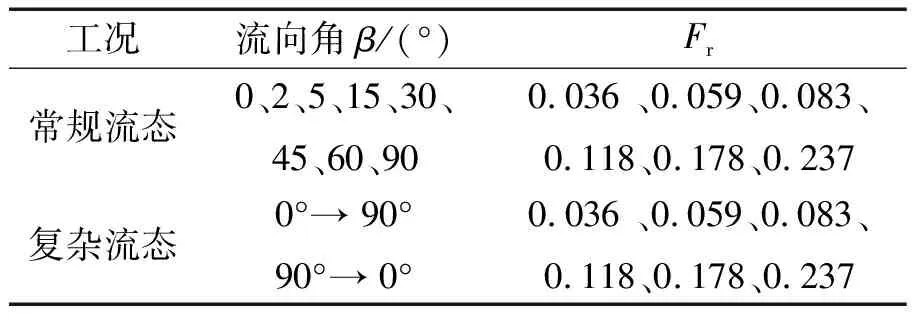
表2 研究工况Tab.2 Calculation conditions

1.5 研究工况

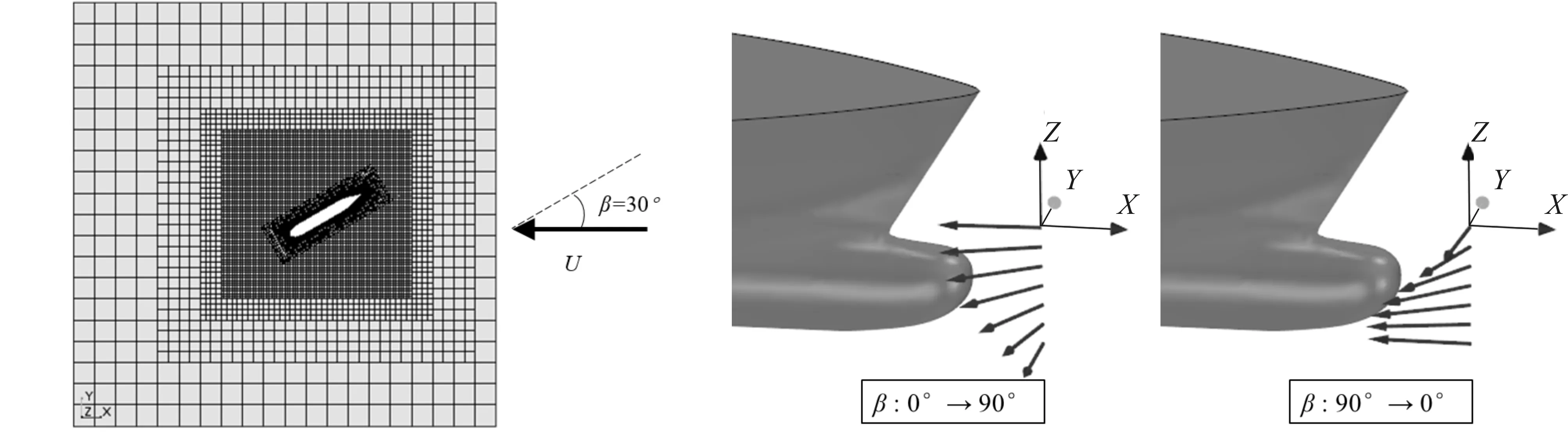
计算工况如表 2所示。常规流态指水流方向单一的水流环境，具体工况包括不同流向角和不同弗劳德数的组合，通过旋转重叠区域改变系泊船姿态，实现水流流向的变化，见图 4。复杂流态为不同弗劳德数下，水流流向分别沿船舶吃水深度从0°方向转变到90°方向以及从90°方向转变到0°方向的水流，通过CFD软件中自定义函数实现，其表达式见式(3)，复杂流态示意图见图5。

(3)

式中：vx、vy分别为水流在x和y方向的速度分量；z为垂向位置；h为船舶吃水；v为水流速度。

将本文探讨的复杂流态条件下系泊船纵向力(船长方向)、横向力(船宽方向)以及艏摇力矩进行无量纲化处理，各物理量的表达式如下所示

(4)

(5)

(6)

式中：Fx、Fy、N、Cx、Cy、CN分别为纵向力、横向力、艏摇力矩及其无因次系数；ρ、U、A、Lpp分别为流体密度、流速、系泊船湿表面积及型长。

2 数值方法验证

2.1 网格无关性检验

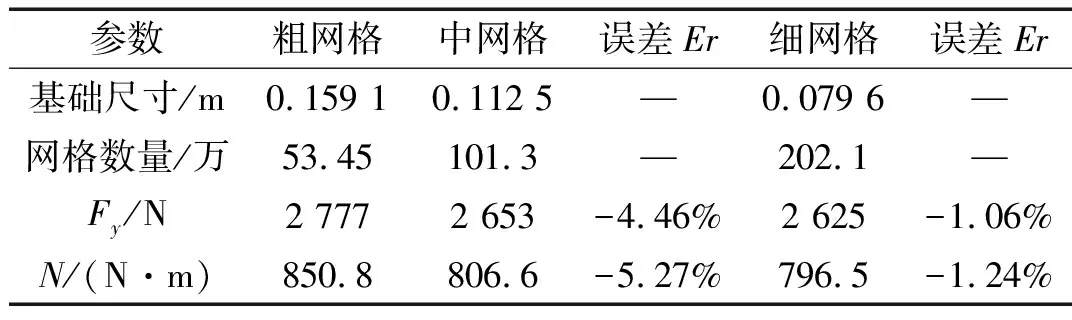
表3 网格无关性分析结果Tab.3 Grid independence analysis results

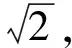
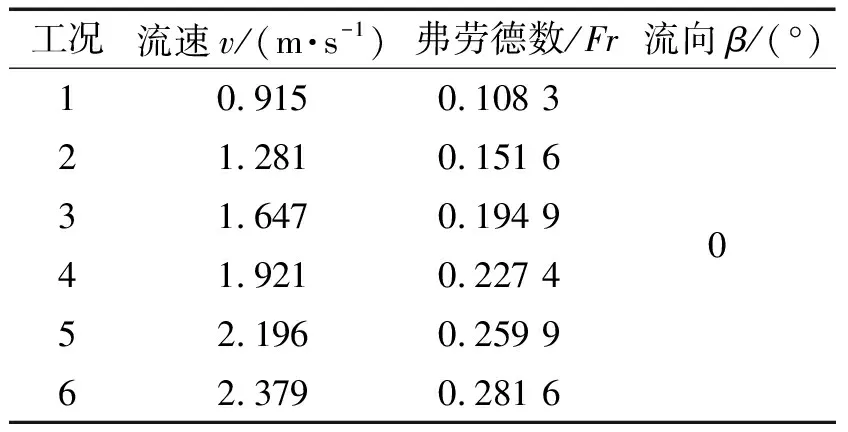
表4 试验工况Tab.4 Experimental conditons

2.2 可靠性验证

采用Tokyo 2015会议中的试验工况进行数值模拟，并将得到的系泊船纵向力系数、纵摇及垂荡的数值计算结果与试验结果进行比较，试验工况见表 4。

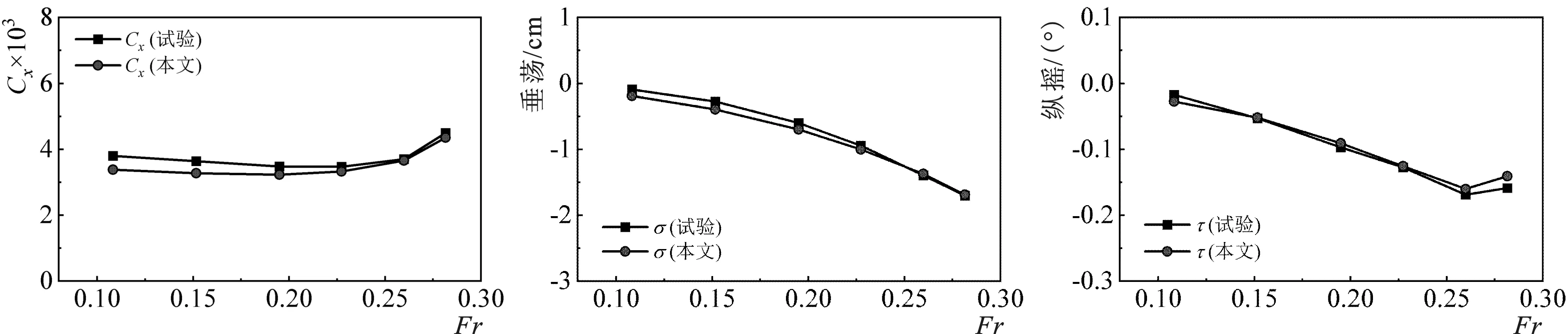
图6给出纵向力系数数值计算结果与Tokyo 2015会议中试验数据的对比。从图中可以看出，系泊船纵向力系数Cx(本文)与试验数据Cx(试验)随Fr变化的趋势一致；Cx(本文)的整体数值相比于Cx(试验)较小；在高弗劳德数下吻合较好，低弗劳德数下存在一定偏差，但是误差百分比均在10%以内。

图7给出不同流速下系泊船垂荡和纵摇数值结果与试验结果的对比。从整体上来看，不同Fr下数值结果与试验结果符合良好。以上研究表明，本文所采用的数值模型能够比较准确地预报系泊船的水动力以及运动响应。

3 数值结果与讨论

3.1 常规流态下系泊船的水动力特性

3.1.1 水动力系数

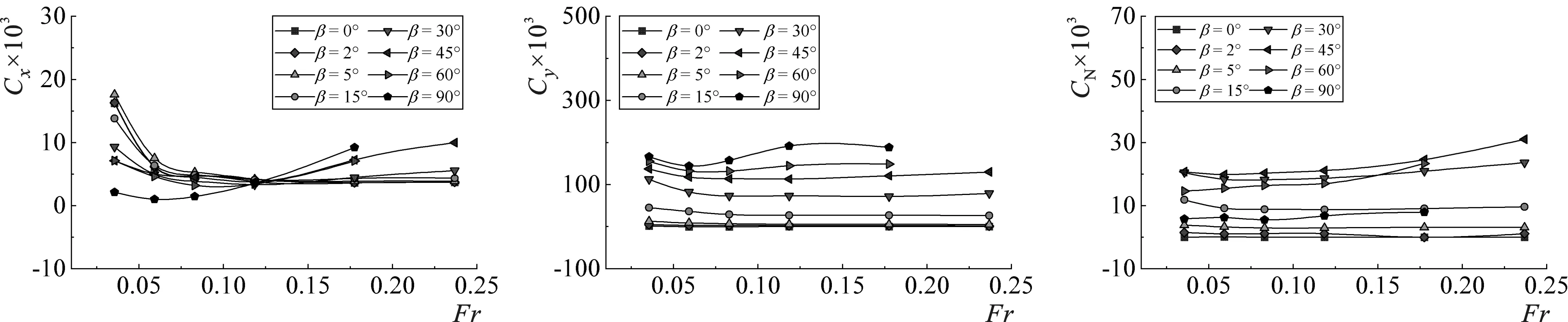
图8给出不同Fr下系泊船水动力系数随β的变化曲线。随着β的增大，系泊船纵向力系数Cx的变化较为复杂：当Fr=0.036～0.118时，Cx整体呈现先增大然后逐渐减小的趋势；当Fr=0.178～0.237时，随着β的增大，Cx的变化曲线整体呈现出逐渐增加的趋势，β较大时系泊船艏艉两侧的流场较为复杂，系泊船纵向力系数受到较大影响。随着β的增大，横向力系数Cy一致呈现逐渐增大的趋势，在β=90°时达到最大值，β的增大使船体逐渐受到侧向水流力的作用，系泊船受力主要以横向力为主。随着β的增大，艏摇力矩系数CN呈现先增大后减小的趋势，基本关于β=45°对称，并且在β=45°达到最大值。随着β的增加，系泊船侧面受到水流作用，受力面积逐渐增大，系泊船从以受纵向力为主转变为以横向力为主，在β>15°后更为明显。需要注意的是，当流向角较大(如β=60°、β=90°)且流速较大(Fr=0.237)时，系泊船因横摇过大而发生倾覆(该工况下的数值结果在文中图表中并未显示)。因此，在实际工程中如面临类似的水流环境，需重点关注。

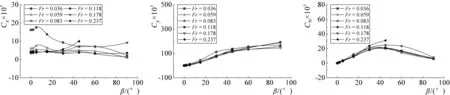
图9给出不同β下系泊船水动力系数随Fr的变化曲线。从图中可以看出，Cx随Fr的变化受到β的影响：当β等于0°～30°时，随着Fr的增大，系泊船纵向力系数Cx呈现逐渐减小至平缓的趋势；当时当β等于45°、60°、90°时，Cx随着Fr的增大呈现先减小后增大的趋势。随着Fr的增大，系泊船横向力系数Cy以及艏摇力矩系数CN的变化较小。

3.1.2 运动响应

图10中给出系泊船在不同Fr下的垂荡、纵摇和横摇随β的变化曲线。随着β的增加，系泊船逐渐下沉，系泊船垂荡值和纵摇值也逐渐增加，但增加的速率逐渐减小。随着β的增加，系泊船横摇值呈现先减小后增大的趋势，在β=0°～45°时横摇值出现负值，然后在β=45°附近转为正值并逐渐增大，当Fr=0.237和0.178时，系泊船横摇值的变化幅度更大。

图11给出Fr=0.178时不同β下系泊船横摇情况及自由面变化。从图中可以看出，当β=0°和30°时，系泊船迎流侧水位变化不大(虚线框内)，水流对系泊船的作用点在船舶质心以下，使得系泊船横摇值出现负值；当β=60°和90°时，系泊船对水流的阻碍作用加剧，在没有缆绳对横摇进行约束的情况下，系泊船迎流面处的水位升高，水流对系泊船的作用点升至质心之上，使系泊船横摇值转为正值，并且随着β的增加逐渐增大。图12给出了Fr=0.178时不同β下系泊船底部压力分布。从图中可以看出，随着β的增加，系泊船迎流侧船舭处压力逐渐变小，船底低压区范围逐渐增大，使得系泊船的垂荡值与纵荡值增加。

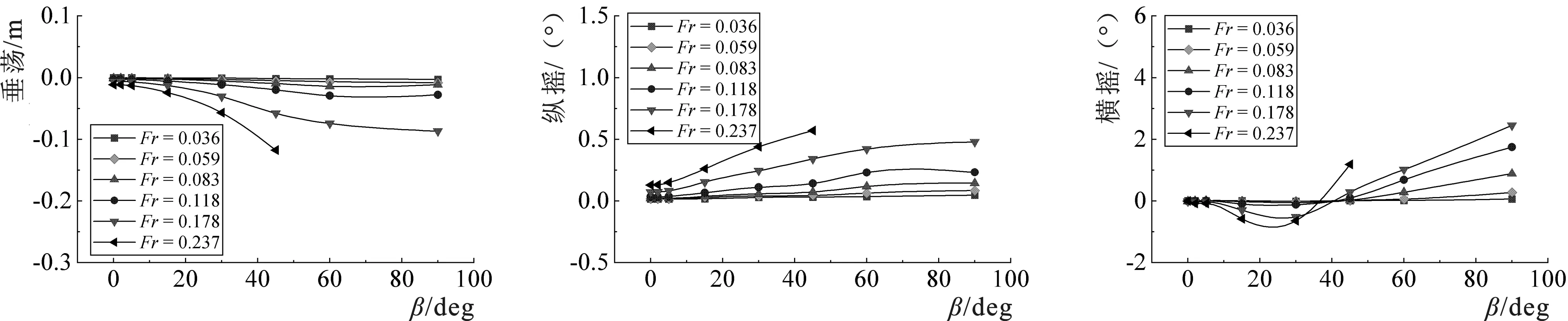
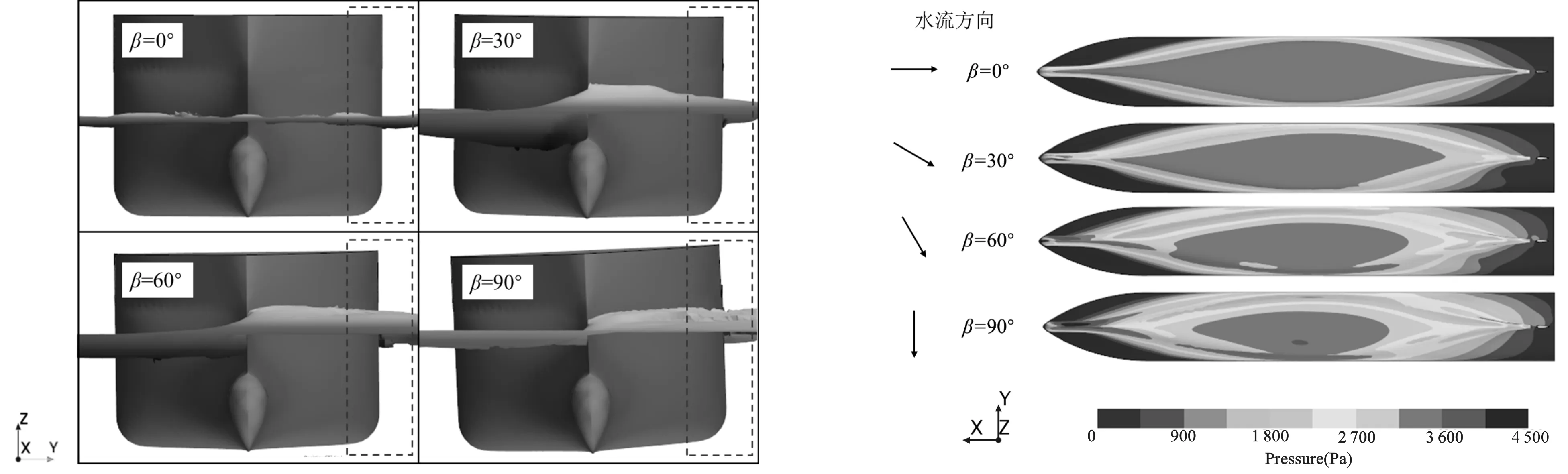
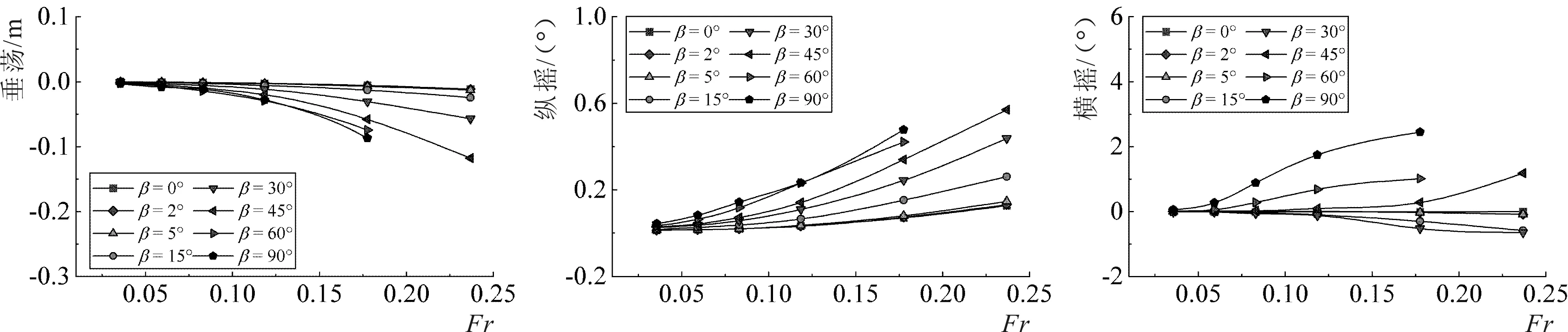
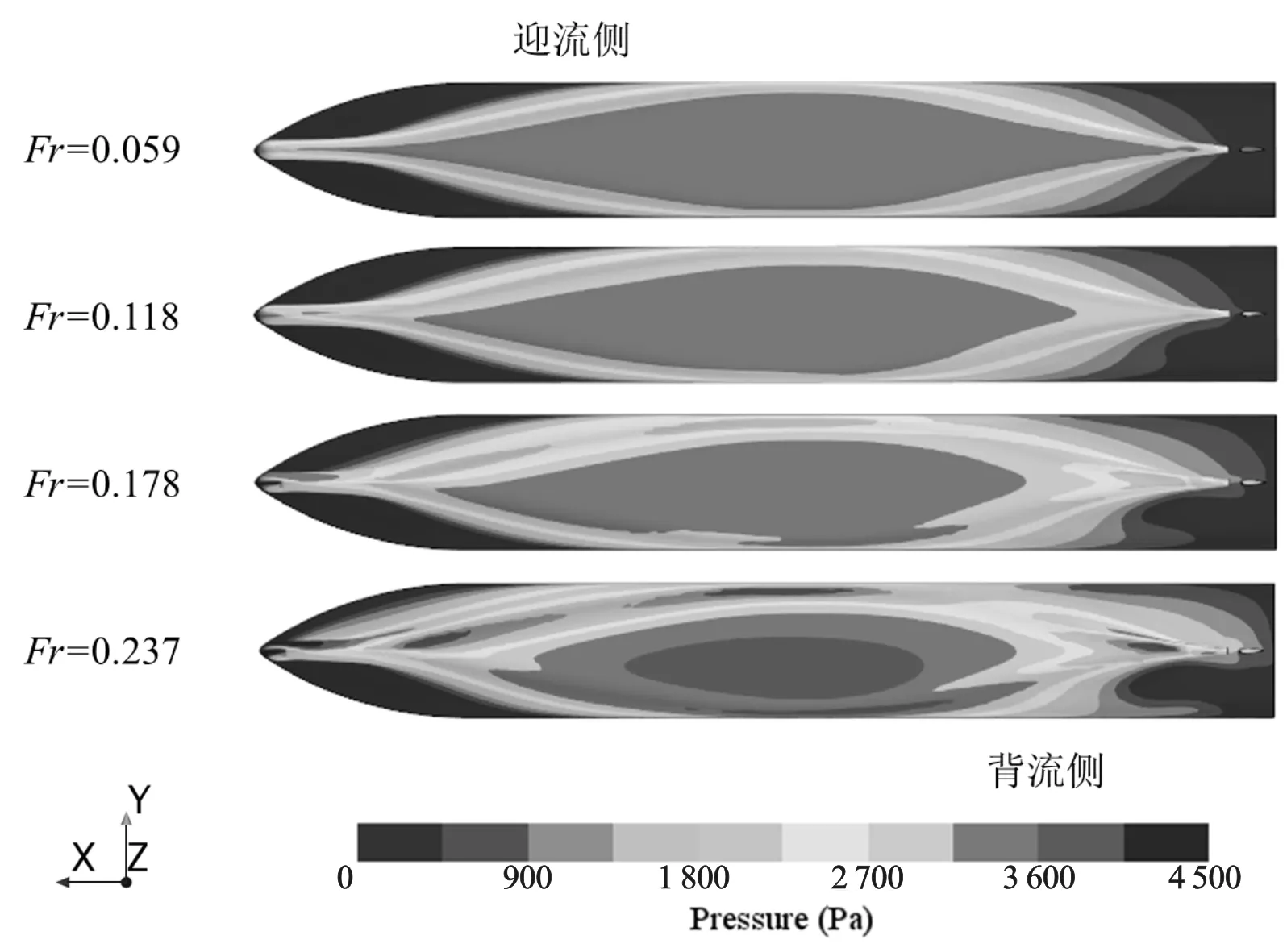
图14 β=45°时不同Fr下系泊船底部压力分布Fig.14 Bottom pressure distribution of mooring ship under different Fr when β= 45°

图13给出系泊船在不同β下的垂荡、纵摇和横摇随Fr变化的曲线。随着Fr的增大，系泊船垂荡值和纵摇值也逐渐增大，增加的速率也逐渐增大。另外，Fr的增大使船体迎流面受力增加，造成船体较大的纵摇。系泊船横摇值变化受水流流向的影响，当β<45°时系泊船横摇值为负，随Fr的增大逐渐减小，当β>45°时系泊船横摇值为正，并随着Fr的增大逐渐增大，其原因与图10中出现负值的原因一致。

图14给出β=45°时不同Fr下系泊船底部压力分布。从图中可以看出，随着Fr的增大，系泊船迎流侧舭部压力减小，背流侧舭部压力增大，船艏和船艉底部低压区面积增大，使系泊船垂荡和纵摇逐渐增大。大流速Fr和大流向角β的组合对系泊船的稳定性更为不利，尤其是当Fr=0.237或0.178且β=60°或90°时，系泊船三个方向的运动量均较大，有较大可能出现安全事故，需要在工程中重点关注。

3.2 复杂流态下系泊船的水动力特性

3.2.1 水动力系数

为明确复杂流态(水流流向角沿水深变化)对系泊船水动力特性的影响，将复杂流态与常规工况系泊船水动力系数和运动响应进行比较，发现在复杂流态作用下，系泊船水动力系数及运动响应随Fr变化的曲线与常规流态中某一流向工况相似。因此，后文在讨论复杂流态下系泊船水动力系数及运动响应时与该工况进行了对比。

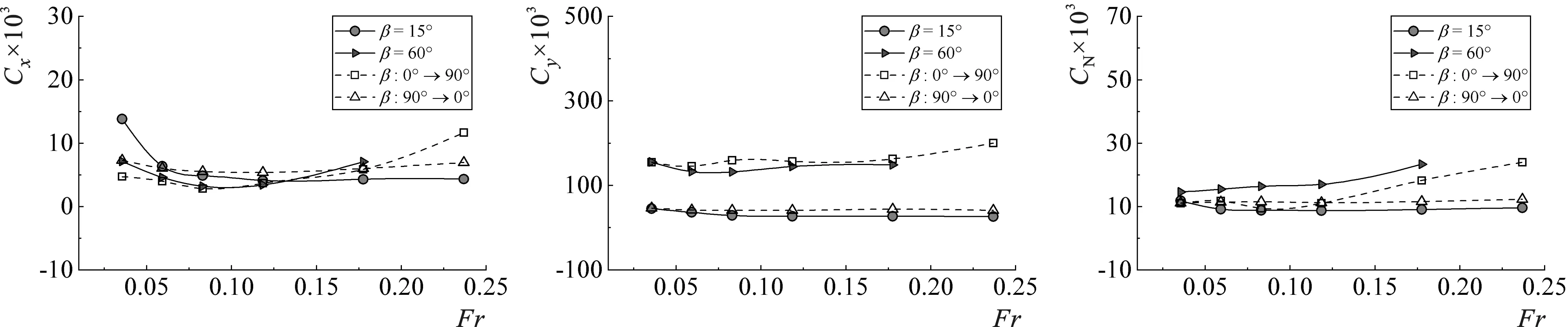
图15给出复杂流态下系泊船水动力系数随Fr变化的曲线。复杂流态下系泊船水动力系数随Fr变化的规律与常规流态工况基本一致。当β为0°→90°时，系泊船的横向力系数Cy、纵向力系数Cx随Fr增大的变化曲线与β=60°时(常规流态)较为接近，艏摇力矩系数CN随Fr增大的变化曲线在Fr=0.118～0.237范围内逐渐上升。当β为90°→0°时，系泊船横向力系数Cy及艏摇力矩系数CN的变化曲线与β=15°时(常规流态)十分接近，但纵向力系数Cx随Fr增大的变化曲线与β=15°时(常规流态)有所差异。另外，β为0°→90°时系泊船的横向力系数Cy要远大于β为90°→0°工况。

3.2.2 运动响应

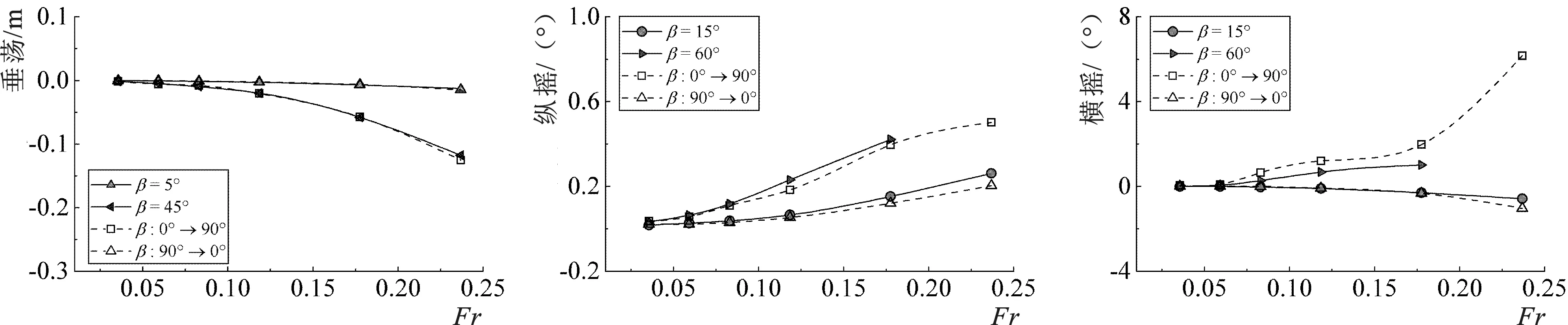
图16给出复杂流态下系泊船运动响应随Fr变化的曲线。从整体上来看，系泊船垂荡、纵摇、横摇随Fr变化的趋势与常规流态工况基本一致，系泊船运动量随Fr的增大而增大。当β为0°→90°时，系泊船垂荡值随Fr增大的变化曲线与β=45°时(常规流态)几乎重合；纵摇值随Fr增大的变化曲线与β=60°的常规流态比较接近，但纵摇值较β=60°小；横摇值随Fr增大的变化曲线与β= 60°或90°工况的常规流态较为相似，在Fr=0.237时横摇值突然增大。当β为90°→0°时，系泊船垂荡值随Fr增大的变化曲线与β=5°的常规流态基本重合；纵摇值随Fr增大的变化曲线与β=15°的常规流态较为接近，但纵摇值较β=15°小。横摇值随Fr增大的变化曲线与β=15°的常规流态基本重合，在Fr=0.237时有所差异。另外，β为0°→90°时系泊船运动响应均大于β为90°→0°工况。

复杂流态下系泊船水动力系数及运动响应变化规律与某一流向角的常规流态工况相似，说明在两种复杂流态工况下，系泊船受到水流作用力会与某一流向角较为接近。另外，系泊船各方向的运动与水动力系数相似的流向角并不完全一致，例如：当β为90°→0°时，系泊船Cy及CN变化曲线与β=15°时十分接近，但是Cx随Fr增大的变化曲线与β=15°时有所差异，这与复杂流态下不同水深处水流流向不同有关。

4 结论

本文基于STAR-CCM+平台，应用计算流体力学方法，通过约束系泊船横荡、纵荡和艏摇三个方向的自由度近似替代缆绳的作用，建立了系泊船简化模型粘性绕流场的数值模型，对常规流态和复杂流态下系泊船模的水动力特性进行了研究，分析了不同流态条件下系泊船水动力系数和运动响应的变化规律，获得了以下主要结论：

(1)常规流态下，随着水流流向角的增大，系泊船纵向力系数变化较为复杂，横向力系数逐渐增大，艏摇力矩系数先逐渐增大后逐渐减小，并关于流向角β= 45°对称。随着水流流速的增大，系泊船纵向力系数变化受水流流向的影响较大，横向力系数和艏摇力矩系数变化较小；(2)常规流态下，随着水流流向角和水流流速的增大，系泊船垂荡和纵摇均逐渐增大，但增大的趋势不同；系泊船横摇值在流向角β< 45°时出现负值，这与系泊船水流作用力的作用点位置有关；(3)复杂流态下，系泊船水动力特性与某一常规流向角工况相似。当β为0°→90°时，水流对系泊船的作用与β≥ 60°的水流较为接近，当β为90°→0°时，水流对系泊船的作用更偏向于水流流向β≤15°的情况。β为0°→90°时系泊船横向力系数及运动响应均大于β为90°→0°工况，说明在实际工程中，β为0°→90°的复杂流态条件对系泊船泊稳安全的影响更大，应对此工况重点关注，并且在研究类似复杂流态条件下系泊船水动力特性及系缆布置时，可以按照某一相似流向的水流工况进行近似处理或参考；(4)当水流流速Fr=0.237且水流流向角β=60°或90°时，系泊船因横摇值较大发生倾覆，严重威胁系泊船的泊稳安全，在实际工程中应给予重点关注。