基于蚁群算法的列车节能驾驶策略优化算法研究

褚心童,张亚东,郭 进,高 豪,李 耀,刘芯宏

(1.西南交通大学信息科学与技术学院,成都 611756； 2.电子科技大学光电科学与工程学院,成都 611731)

近年来，随着中国城市轨道交通的蓬勃发展，运输能耗成本也日益增加。虽然相较于其他交通方式，同等运力下轨道交通能耗仅为小汽车的1/9，公交车的1/2，但由于实际运量大，其总能耗依旧十分巨大[1]。根据中国城市轨道交通协会统计，2018年北京城市轨道交通路网耗能约19亿kW·h，年均增长近9.20%[2]。另外，城市轨道交通系统的能耗主要分为列车牵引能耗和动力照明能耗，其中列车牵引能耗占总能耗的50%～60%[3]。因此，降低列车牵引能耗，对城市轨道交通企业节能降耗具有重要现实意义。

目前轨道交通系统中，对列车驾驶策略的优化是减少列车运行能耗的主要方法之一[4]。卫东等进行了多目标ATO驾驶策略的优化研究，并提出巡航工况模式相较于组合工况模式耗能较高[5]；张勇等研究了惰行距离的延长对节能的影响[6]。同时，智能算法的引入为列车目标速度曲线的寻优提供了更好的解决方案，学者采用人工蜂群算法[7]、粒子群算法[8]、遗传算法[9]、模糊PID算法[10]等，对驾驶曲线进行了节能优化方面的研究工作。

国内外学者虽然在驾驶策略改进和目标速度曲线优化方面进行了广泛的研究，但在ATO驾驶策略中往往使用巡航工况对目标速度进行精准跟踪，耗能较大[11]；传统曲线优化采用的各类智能算法由于计算分区多、缺乏收敛方向引导，存在计算速度慢、算法效率低的问题[12]。

综上所述，从优化列车目标速度曲线和改进ATO驾驶策略两方面对降低列车牵引能耗进行了综合研究。首先建立推荐速度曲线优化模型，给定运行约束条件；其次使用蚁群算法，结合司机驾驶经验，引导算法收敛方向，对列车推荐速度曲线进行多目标优化；然后提出节能巡航驾驶策略，对原有ATO驾驶策略进行优化，以达到节能目的；最后结合北京地铁亦庄线数据实现算法的仿真与验证。

1 列车推荐速度曲线优化建模

1.1 列车动力学方程

列车在运行过程中，其受力可大致分为4类：重力G，列车牵引力F，列车制动力B和列车运行总阻力W，如图1所示[13]。

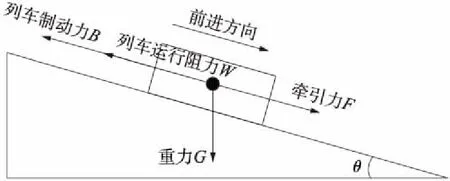
图1 单质点列车受力分析示意

列车牵引力是列车运行的动力，是与列车运行方向相同并可以根据运行状况人为控制的外力。牵引力F在不同速度下存在不同的最大值Fmax=fF(v)。

列车制动力是与列车运行方向相反、阻碍列车运行且可以由司机根据需求进行调节的外力。制动力B在不同速度下存在不同的最大值Bmax=fB(v)。

列车运行阻力W是与列车运行方向相反且不可以由司机控制的外力。根据列车运行中产生阻力的原因，运行阻力可分为基本阻力和附加阻力。基本阻力是在运行过程中一直存在的阻力，其单位阻力计算公式如式(1)所示，附加阻力是在个别情况下产生的阻力，如坡度附加阻力、曲线阻力、隧道阻力等，其单位阻力计算公式分别如式(2)、式(3)、式(4)所示。

w0=a+bv+cv2

(1)

wi=i

(2)

wr=600/R

(3)

ws=0.000 13Ls

(4)

式中，a、b、c为与机械阻力有关的经验常数；v为列车速度，m/s；i为列车所在坡道的千分数；R为曲线半径，m；Ls为隧道长度，m。

综上所述，列车运行总阻力为

W(v)=(w0+wi+wr+ws)×g×M

(5)

其中，g为重力加速度，通常取9.8 m/s2；M为列车质量，kg。

理想状态下，单质点列车运动方程可描述为

ct=fF(vt)-fB(vt)-W(vt)

(6)

其中，ct为时间t时列车所受合力；vt为列车运行速度。

1.2 能耗计算方程

列车在站间运行时根据所在位置的线路数据获取限制速度，限制速度周期性更新，列车运行过程中不允许超过该限制速度，期间通常包含4种运行工况：牵引、巡航、惰行和制动[14]，如图2所示。

图2 站间运行示意

牵引阶段：列车加速，发动机处于耗能状态，计算公式如式(7)。式中，E为牵引能耗，T为运行时间，F(t)为t时刻的牵引力；v(t)为t时刻的列车运行速度。

(7)

巡航阶段：列车匀速运行所受合力为0，发动机能耗取决于列车运行总阻力，计算公式同式(7)。

惰行阶段：列车既不牵引也不制动，列车运行状态受列车运行总阻力影响，发动机不耗能。

制动阶段：列车减速，发动机不耗能。

1.3 推荐速度曲线优化模型

1.3.1 连续变量的离散化

本文使用蚁群算法的离散组合优化技术对推荐速度曲线进行寻优，该方法要求对模型中的连续数据进行离散化处理，包括站间线路数据和速度数据的离散化，如图3所示。

图3 线路数据离散化示意

传统线路数据离散化方式采取距离等分法，但该方法容易造成同一区段上线路数据不唯一的问题，导致计算困难。因此提出将线路基于限速、坡度、曲率数据离散化为N个区段，保证每个离散化区段上的各线路数据为常数，便于算法计算。

为方便计算，可将列车所在位置的最大允许速度等分离散为M个等级的速度码，表示为

Vm={m×VM/M，m=1，2，…，M}

(8)

1.3.2 目标及约束

根据上述分析，推荐速度曲线优化模型为

(9)

可以看出，本模型将总长度S的列车运行线路划分为N个离散段，(sj-1，sj]表示从位置sj-1到位置sj的区段Xj，同一区段上任意位置限速vk、曲线半径Rk、坡度ik均为常数；将列车所在区段Xj的最大允许速度vmax等分为M个速度等级，并从中选取区段Xj的推荐速度码，用Vj表示；同时列车实际运行时间T应与计划运行时间Td保持在允许误差范围内；列车在区段Xj的运行能耗用Ej表示。

2 基于蚁群算法的推荐速度曲线优化

经过离散化建模，列车推荐速度曲线节能优化问题可转化为多目标下的寻优问题。本文采用最大最小蚁群算法对问题进行优化求解。

最大最小蚁群算法是蚁群算法的改进算法，通过控制信息素设置范围、初始值及信息素释放规则等，避免了算法过早停滞，提高了搜索能力，对组合优化问题具有良好的适应性[15]。

在列车节能优化问题上，最大最小蚁群算法主要具有以下优势。

(1)利用其分布式计算、近似计算的特点，对推荐速度曲线进行离散组合寻优。

(2)优化收敛速度快。

(3)启发信息素的设置可与司机驾驶经验相结合，适应行业特点，提高优化能力。

2.1 数据初始化

2.1.1 线路数据读取并处理

首先读取线路数据，包括线路限速、坡度、曲率信息。由于列车在启停阶段的实际运行速度可能远小于线路限速，直接使用线路限速进行速度数据离散化会产生大量不可行解，降低算法效率。因此先计算列车站间运行时间最短的最速曲线，再根据最速曲线和坡度、曲率信息完成线路数据和速度数据的离散化。

2.1.2 算法参数设定

初始化蚂蚁数量Ant_Num、信息素矩阵τ、算法最大迭代次数NC_max。

2.1.3 基于司机驾驶策略的启发信息素设置

启发信息素的设置对蚂蚁搜索下一离散区段路径的概率有一定影响，可以改变搜索方向，加快算法收敛速度[16]。在实际驾驶中，司机在下坡时偏向加速，上坡时偏向惰行[17]，本文据此制定启发信息素设置原则，如表1所示，有效改善算法性能。

表1 基于司机驾驶策略的启发信息素设置原则

2.2 迭代过程

在算法设计中，每只蚂蚁相当于一列列车，各蚂蚁互相独立。每次迭代过程相当于一次推荐速度曲线计算过程，该过程包含N步，N为站间离散化区间数目。每只蚂蚁在各区段中按照路径选择规则选取速度等级并完成追踪运行，计算能耗数据。每代能耗最低的蚂蚁称为当代最优蚂蚁，历史迭代最优蚂蚁称为至今最优蚂蚁。

2.2.1 路径构建

在每个离散化区段上，列车以上一区段末速度作为初速度，结合线路数据、车辆数据计算本区段可达到的末速度范围，并根据路径选择规则，选取一个可行的末速度作为本区段推荐速度。重复N次后，即可获得一条推荐速度曲线。

路径选择规则采用随机比例原则，其计算公式如下

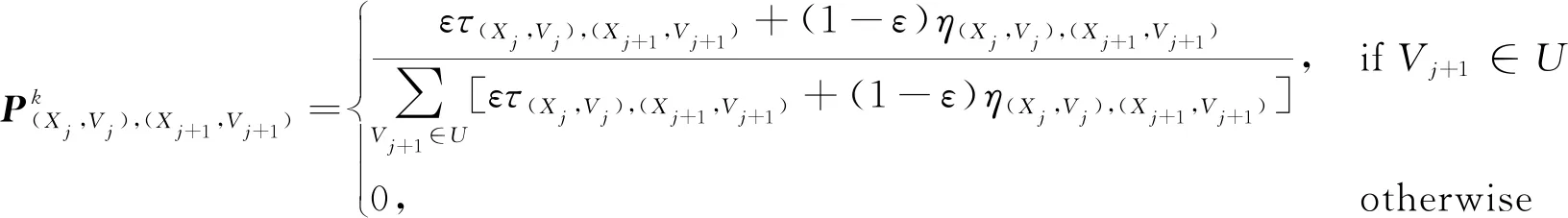
(10)

2.2.2 评价数据计算和筛选

完成一代中所有蚂蚁的路径构建后，可计算列车在每条路径运行的能耗及时间。若某路经不满足运行时间限制，则该路径为不可行解，应予以舍弃。其余蚂蚁中，能耗最低的蚂蚁作为当代最优蚂蚁，并将其与至今最优蚂蚁的能耗进行比较，若当代最优蚂蚁能耗较低，则更新至今最优蚂蚁数据。

2.2.3 信息素更新

根据当代最优蚂蚁和至今最优蚂蚁数据，按下述式(11)规则完成信息素更新。

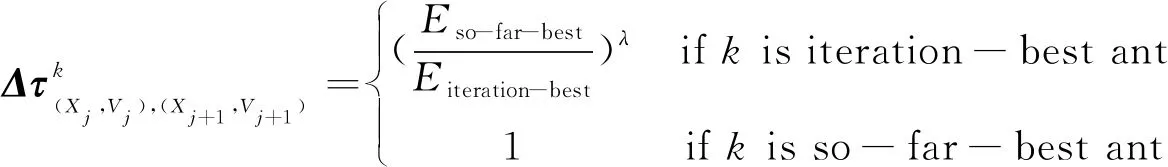
(11)

2.2.4 算法终止条件

当迭代次数超过算法设置的最大迭代次数时，结束运算。此时的至今最优蚂蚁对应的推荐速度曲线就是算法优化的最终结果。

2.2.5 算法流程图

本优化算法的详细流程如图4所示。

图4 线路数据离散化示意

3 ATO驾驶策略改进

传统的ATO驾驶策略中，列车完成起步牵引，运行速度达到推荐速度后会切换至巡航工况继续运行，保持对推荐速度的精准跟踪[18]。但由于实际列车运行控制级位的约束，长时间使用精准巡航工况会反复实施牵引力和制动力的转换，能耗较大[19]。因此将巡航工况拆分成多个牵引-惰行组合工况，实现节能巡航，如图5所示。

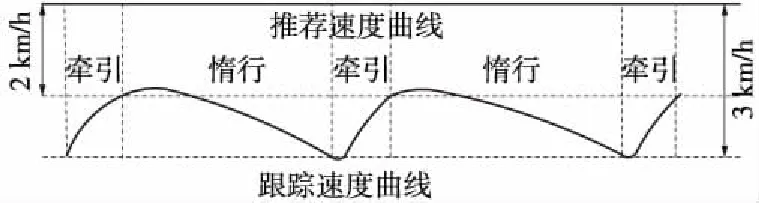
图5 ATO巡航控制策略示意

当推荐速度与实际运行速度差值小于2 km/h时，列车切除牵引转为惰行工况，在节能的同时防止列车超速运行，保证行车安全；当差值大于3 km/h时，列车再次施加牵引，提升列车运行速度，保证列车站间运行时间。

4 仿真计算与结果分析

本文基于北京地铁亦庄线实际数据，对该算法进行仿真验证。

4.1 线路数据

北京地铁亦庄线的实际线路数据和运营数据见表2[20]。

表2 北京地铁亦庄线实际线路运营数据

4.2 车辆数据

北京地铁亦庄线常用车型的牵引制动特性曲线经多项式拟合后，得到最大牵引力为[21]

(12)

最大制动力为

(13)

其他相关车辆性能参数见表3[22]。

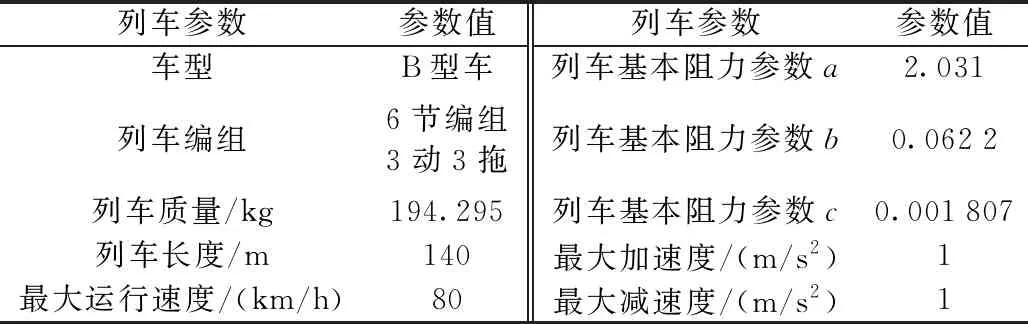
表3 车辆性能参数

4.3 算法参数设置

在蚁群算法寻优中，涉及到的重要参数设置值见表4。

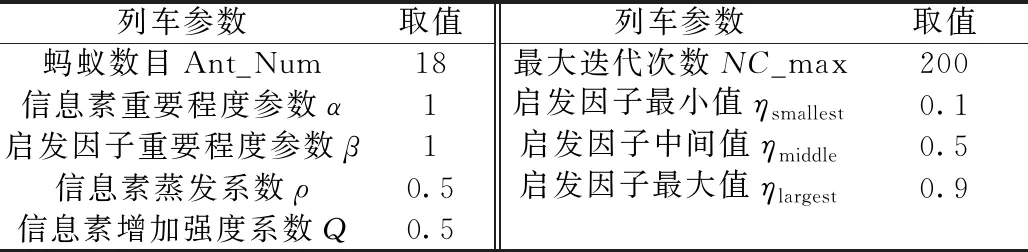
表4 算法参数设置

4.4 仿真结果分析

以列车上行亦庄文化园站到万源街站为例，根据线路数据统计，未优化的列车站间实际运行消耗15.3 kW·h，站间运行时间144 s。为验证本文结合司机驾驶经验的蚁群算法和ATO节能巡航驾驶策略有效，使用Matlab R2018b进行两次仿真对比。

首先，不加入司机驾驶策略，仅采用常规蚁群算法对推荐速度进行优化，获得的蚁群算法优化曲线如图6(a)所示，算法收敛情况如图6(b)所示。此时，列车消耗能耗12.779 2 kW·h，节能效果约16.48%，列车走行时间126.24 s，满足运行时刻要求。算法迭代20次后收敛，计算时间消耗1.348 8 s。

然后，引入司机驾驶经验，即采用表4中启发因子参数对蚁群算法进行参数整定，优化后的蚁群算法优化曲线如图6(c)所示，算法收敛情况如图6(d)所示。此时，列车消耗能耗12.647 6 kW·h，节能效果提升至17.16%，列车走行时间130.417s。算法迭代次数下降至17次，计算时间下降至1.327 7 s。由此可见，结合司机驾驶经验，在能耗降低方面效果虽不明显，但能使蚁群算法收敛速度加快，引导算法搜索方向，提升整体算法的优化性能。

最后，采用ATO节能巡航驾驶策略，对图6(c)中蚁群算法优化曲线进行仿真追踪运行，获得的ATO节能驾驶优化曲线如图6(c)所示。经计算，列车消耗能耗11.792 6 kW·h，节能效果进一步提升至22.92%，列车走行时间137.243 3 s，满足运行时刻要求。由此可见，引入ATO节能巡航驾驶策略，虽延长了部分走行时间，但能大幅提升节能效果。

综上所述，结合司机驾驶经验的蚁群算法较常规蚁群算法收敛速度更快，算法性能更好，与ATO节能巡航驾驶策略合并使用，可以获得更好的节能效果，为后续研究提供了新思路。

图6 亦庄文化园站—万源街站仿真运行曲线及算法收敛情况

5 结论

针对城市轨道交通中列车牵引能耗大的问题，建立推荐速度曲线优化模型，使用结合司机驾驶经验的蚁群算法和ATO节能巡航驾驶策略对ATO控制曲线进行优化，最后使用北京亦庄线实际运营数据进行仿真验证。结果显示，使用该算法优化后，列车站间牵引能耗可下降22.92%，节能效果明显。同时，本算法计算消耗时间仅为1.3277s，收敛速度快。上述结果验证了该算法在列车节能驾驶策略优化方面的有效性。