基于发电机组最大调节速率的电网负荷指令调度优化

魏梦瑶,王建东,杨子江

(山东科技大学电气与自动化工程学院，青岛 266590)

随着新能源产业的快速发展，大规模风电、光伏等并网发电。但新能源具有间歇性、波动性、周期性等特点，并网后加剧了电网频率波动，对电网稳定运行带来挑战。通过建设大规模储能系统[1-2]，增大跨区域外送[3]、优化新能源调度[4]、改进光伏电站功率控制策略[5]等措施可以减少弃风、弃光现象，提升电网新能源消纳能力。

自动发电控制(automatic generation control，AGC)能在大负荷变化或其他干扰下维持系统频率稳定性，是提高电力系统安全性的辅助服务之一。当电网频率波动时，根据电网功率偏差产生一个总AGC指令，电网调度中心依照某种分配方法把总AGC指令分配给每台机组，然后，机组通过增大或减少出力，消除电网功率偏差，保证电网安全稳定运行。所以，依据机组运行特性，建立科学合理的负荷调度策略，对于电网平稳运行和新能源发电消纳具有重要意义。

在实际电网AGC指令分配方面，电网调度中心通常采用平均分配法，高宗和[6]提到了按机组容量和按机组响应速率将总AGC指令分配到每台机组；Chen等[7]依照发电机组对降低电网功率误差的贡献率，提出了一种按机组容量平均分配的方法；谢俊等[8]使用多智能体一致性算法，以发电机组的增量成本和柔性负荷的增量效益作为一致性变量，设计了一种用于未来电力系统分布式调度的方法；张孝顺等[9]为了最小化机组的最大爬升时间，使调节速率快的机组承担更多的负荷，采用爬升时间一致性算法解决互联电网AGC功率的动态分配问题，但各台机组之间需要保持信息互联，就目前条件在实际生产中难以广泛应用。

为加快消除电网频率波动，实现大规模新能源并网条件下的电网安全平稳运行，现提出一种基于机组最大调节速率估计的负荷指令调度优化方法。在机组实际运行过程中，机组的最大调节速率与初始设置值是不完全匹配的，所以获得机组真实的最大调节速率是关键。在所提出的AGC指令分配方法中，通过数据挖掘技术从机组的实发功率历史数据中得到最能体现机组真实能力的调节速率样本，首先，对机组实发功率历史数据分段线性表示，由各数据段的幅值变化和持续时间估计机组调节速率样本，采用贝叶斯估计判断调节速率样本分布的稳定性，以获得机组最大调节速率的可靠估计；然后，以最短负荷调节时间为优化目标建立负荷指令调度优化模型，确定按机组最大调节速率分配电网总AGC指令的调度方法；最后，通过实际工业案例和标准电网区域模型仿真，验证该方法的有效性。

1 问题描述

电力调度是结合电网实际运行参数等数据信息，发布操作指令，使机组调整出力，从而确保电网持续安全稳定运行的一种管理手段。如图1所示，调度中心收到一个总AGC指令，在获取机组数据信息的基础上，通过某种优化分配方法将总AGC指令分配到每台机组。

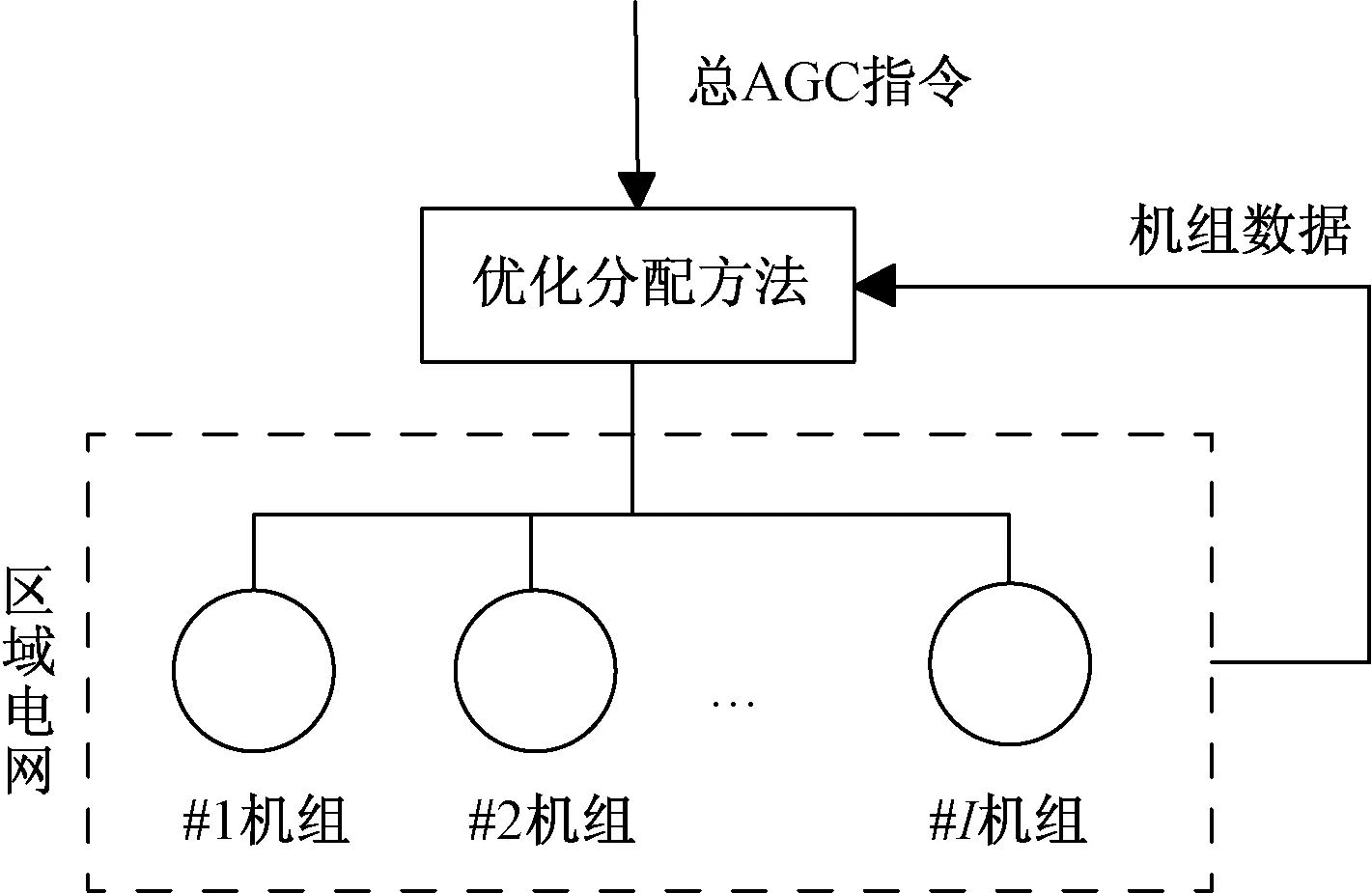
图1 总AGC指令分配结构图Fig.1 The framework of AGC demand dispatched

假设区域电网有I台机组，当前电网总AGC指令的调整负荷为ΔP，通过某种优化分配方法将总AGC指令分配到每台机组。那么，I台机组的调整负荷分别为：ΔP1,ΔP2,…,ΔPI。根据机组调节速率可以计算每台机组的调节时间以及完成电网总AGC指令所需时间。

研究旨在保证电网安全稳定运行的前提下，对电网总AGC指令优化分配，让调节速率快的机组承担更多的调整负荷，使机组能在最短时间内完成负荷调整，消除电网频率波动。

2 最大调节速率

机组最大调节速率指在一段时间内使机组有功功率出力产生上升或下降幅度变化的最快速度。首先，通过分段线性表达技术从机组的实发功率历史数据中得到机组调节速率样本，然后，采用贝叶斯估计判断调节速率样本分布的稳定性，得到机组最大调节速率估计。

2.1 分段线性表示

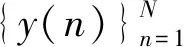
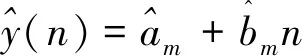
(1)

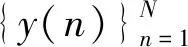
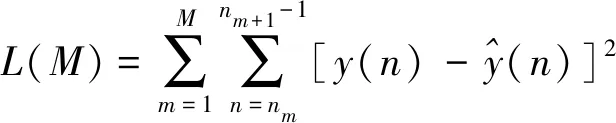
(2)

其中，分段数M可由Keogh等[11]提出的方法确定：

(3)

机组实发功率的PLR结果如图2所示，蓝色为机组实发功率数据，红色线段为PLR结果。第m段数据的幅值变化和持续时间可以表示为

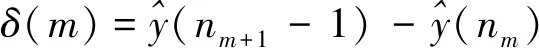
(4)

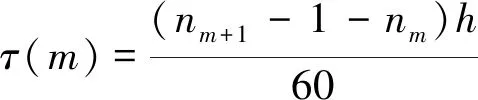
(5)

式中：h为实发功率时间序列的采样周期，s；δ为幅值，MW；τ为时间，min。

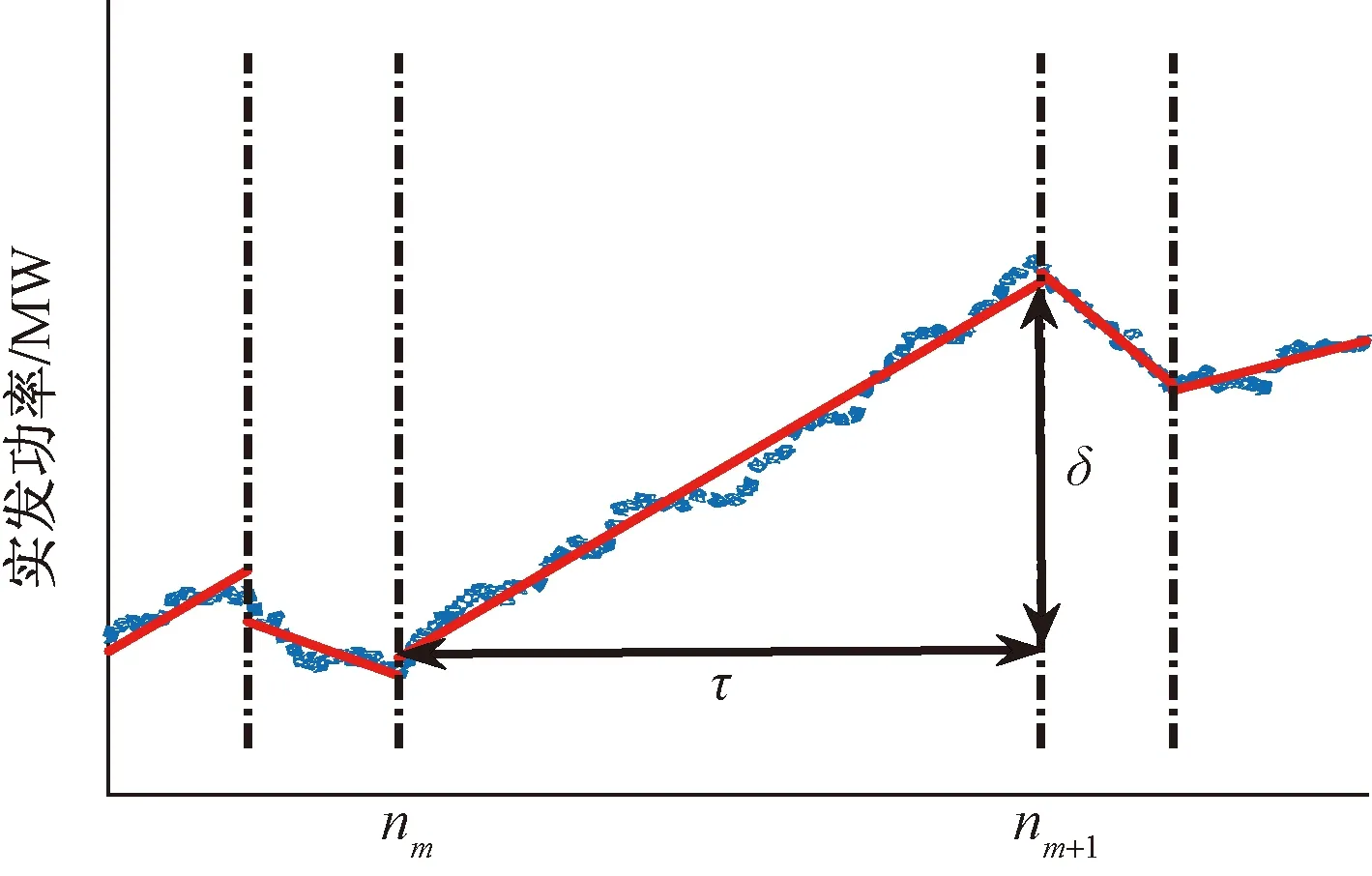
图2 实发功率PLR结果Fig.2 The PLRs of generated active power

第m段数据估计的机组调节速率为

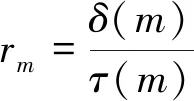
(6)

由所有数据段计算得到机组调节速率，并将它们分为上升速率和下降速率两个速率值集合，表示为

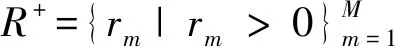
(7)

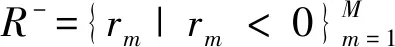
(8)

2.2 贝叶斯估计判断样本分布稳定性

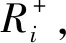
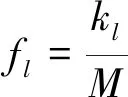
(9)

假设先验分布为均匀分布，即fl～U(0，1)，那么，离散概率密度函数为

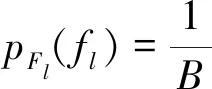
(10)

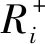
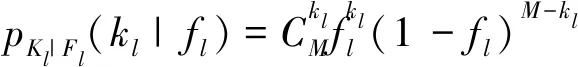
(11)

根据贝叶斯公式，联合分布的概率密度函数为

pKl,Fl(kl,fl)=pKl|Fl(kl|fl)pFl(fl)

(12)

然后，可得到Fl的后验分布

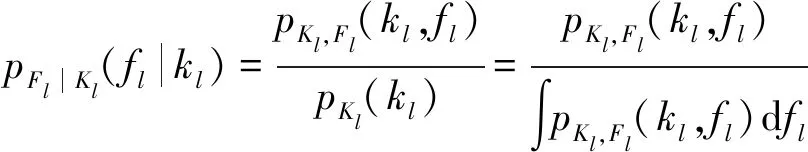
(13)

根据Fl的后验分布，由式(14)可得到fl的1-α置信区间[fl,low,fl,high]，即

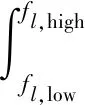
(14)

定义组频率fl的稳定指标判断样本区间分布的稳定性，即

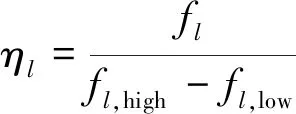
(15)

如果ηl>ηl,th，则认为第l个区间样本稳定。为判断整个集合的样本稳定性，定义样本分布稳定性指标

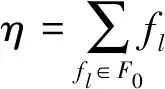
(16)

式(16)中：F0={fl|ηl>ηl,th,l∈[1,L]}，如果η>ηth，则认为集合中样本分布稳定。反之，需要增加集合中样本的数量，重新判断集合中样本稳定性。阈值ηl,th和ηth取决于用户的选择，默认值为ηl,th=3，ηth=0.8。

取pFl|Kl(fl|kl)的(1-β)%分位数为机组最大调节速率的估计，即机组的最大上升速率为

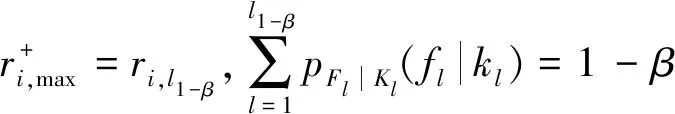
(17)

3 负荷指令调度优化

3.1 线性规划模型

为获得调节时间最短时总AGC指令的分配结果，建立优化模型：

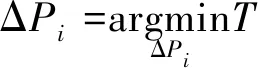
(18)

约束条件为

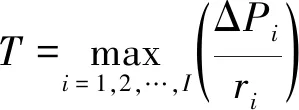
(19)

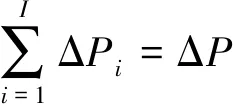
(20)

式中：ΔPi和ri分别为第i台机组的AGC指令调整负荷和最大调节速率；T为电网总调节时间，数值上等于I台机组中最大的调节时间。

3.2 按机组最大调节速率分配

采用拉格朗日乘子法引入拉格朗日算子计算得到模型的最优解。

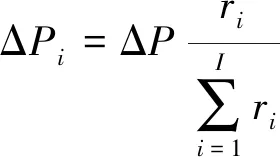
(21)

因此，按机组最大调节速率分配可在最短调节时间内完成总AGC指令。

由于机组的上升和下降速率不同，所以调度优化前，要根据调整负荷ΔP确定第i台机组的最大调节速率。当需要通过增大机组出力才能达到电网总AGC指令要求时，机组最大调节速率取最大上升速率；反之，取最大下降速率。

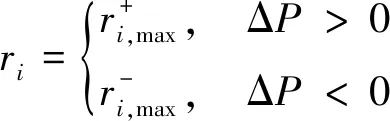
(22)

图3 基于最大调节速率的AGC指令分配流程图Fig.3 Flow chart of AGC demand dispatching based the maximum rates

为确保机组能正常执行AGC指令，第i台机组的调整负荷ΔPi必须在机组可调节范围内，即

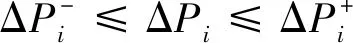
(23)

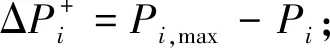
如果第j台机组不满足约束条件式(23)。那么，以当前机组最大可调容量分配调整负荷。然后，剔除第j台越限机组，ΔP更新为

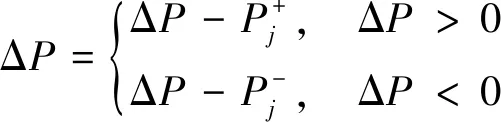
(24)

根据式(21)重新分配ΔP，直到分配给各台机组的调整负荷ΔPi都满足式(23)。

当机组的调整负荷过小时，机组无法根据指令改变出力。为确保机组能正常执行AGC指令，要使调整负荷大于机组最低限值Δp，即

|ΔPi|≥Δp

(25)

其中，不同类型机组的Δp存在差异[12]。

如果第j台机组的调整负荷小于Δp，则剔除第j台机组，由式(21)对总AGC指令调整负荷ΔP重新分配，直到各台机组的调整负荷满足式(23)、式(25)，得到最终的分配结果。

综上所述，基于机组最大调节速率对总AGC指令优化分配的算法流程如图3所示，可以简述为以下步骤。

步骤1：根据式(21)计算每台机组的AGC指令调整负荷为：ΔPi,i=1,2,…,I。

步骤2：判断ΔPi是否满足式(23)，如果不满足，剔除越限机组并更新ΔP，重复步骤1～步骤2。

步骤3：判断ΔPi是否满足式(25)，如果不满足，剔除越限机组，重复步骤1～步骤3。

4 方法验证

4.1 工业案例

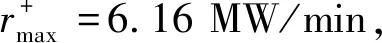
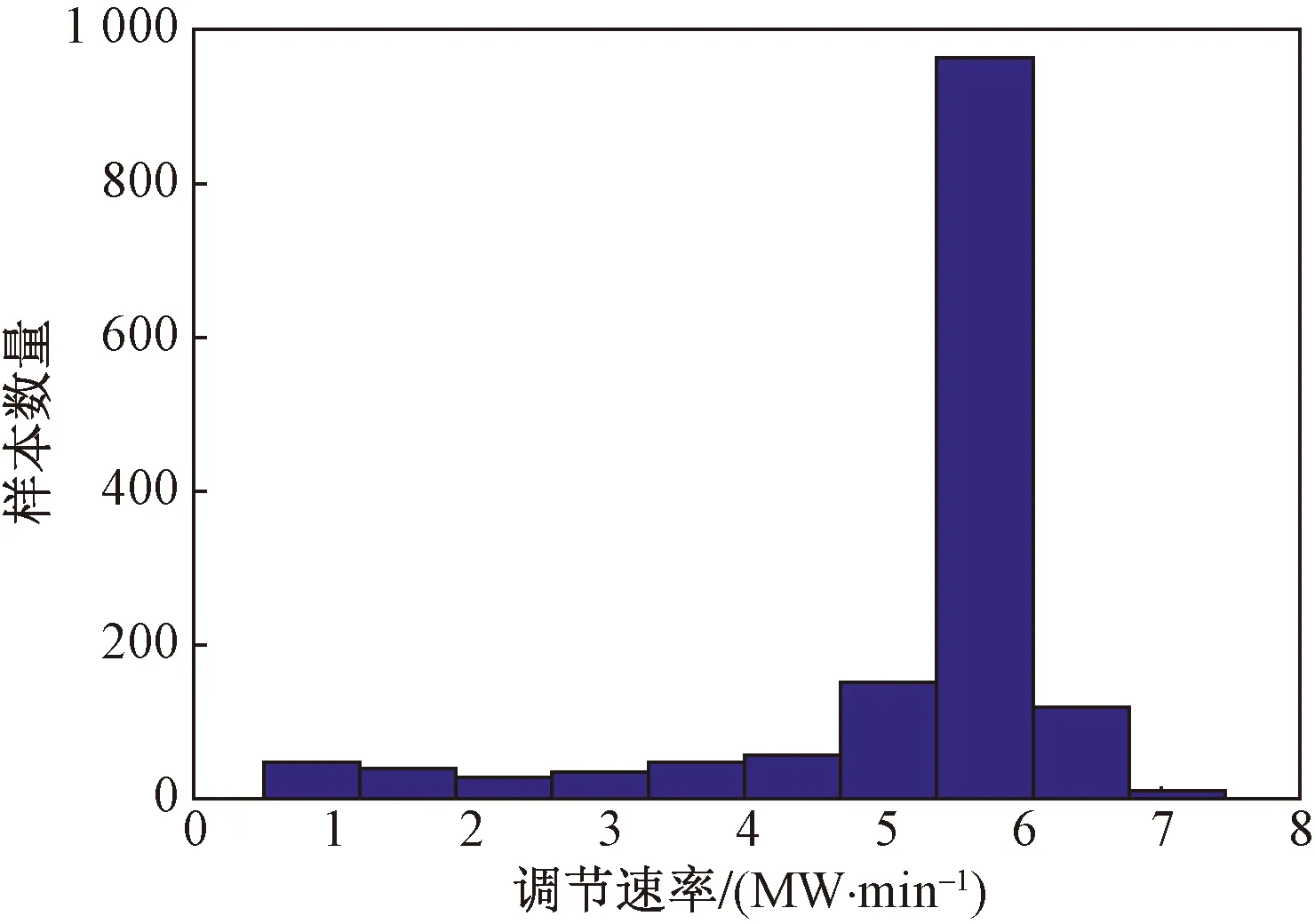
图4 调节速率样本分布图Fig.4 The distribution map of ramp rate samples

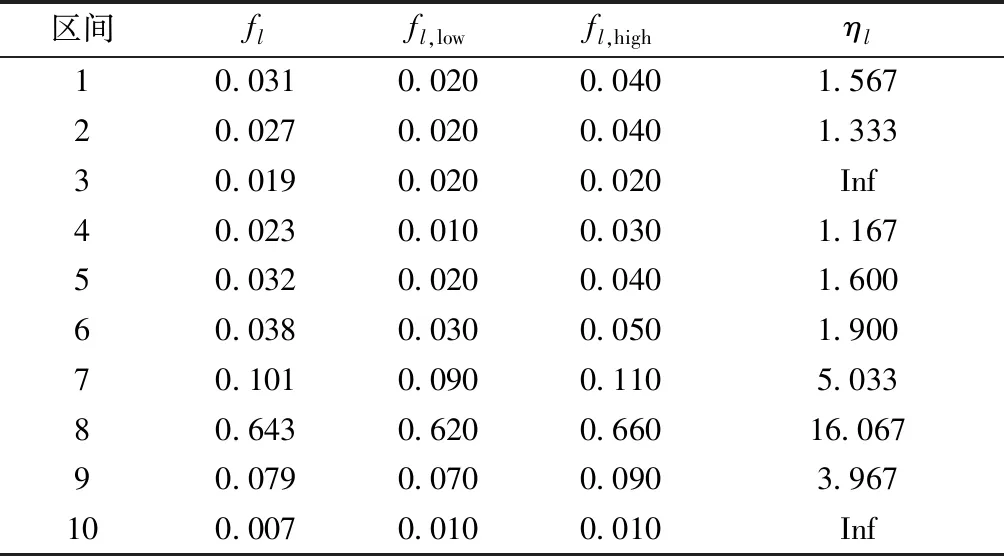
表1 样本区间的相关指标Table 1 The interval’s relevant indicators

4.2 仿真案例

使用Simulink搭建一个标准单区域模型[13-14]，其中，区域内5台机组的基本参数如表2所示，案例1和案例2在不同状态下仿真验证本文方法的有效性，案例3与现有分配方法进行对比。

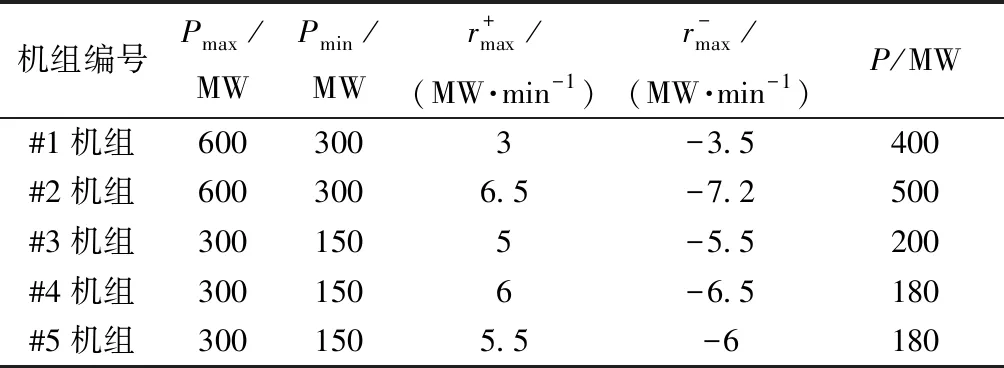
表2 发电机组基本参数Table 2 Parameters of power generation units

4.2.1 仿真案例1

当区域电网总AGC指令调整负荷为ΔP=10 MW，根据式(21)分配给5台机组的调整负荷分别为1.15、2.5、1.92、2.31、2.12 MW。#1机组负荷调节的最低限值Δp=1.2 MW，显然，#1机组不满足约束式(25)，剔除该机组，保持总AGC指令的调整负荷ΔP不变，最终的分配结果为0、2.8、2.2、2.6、2.4 MW。

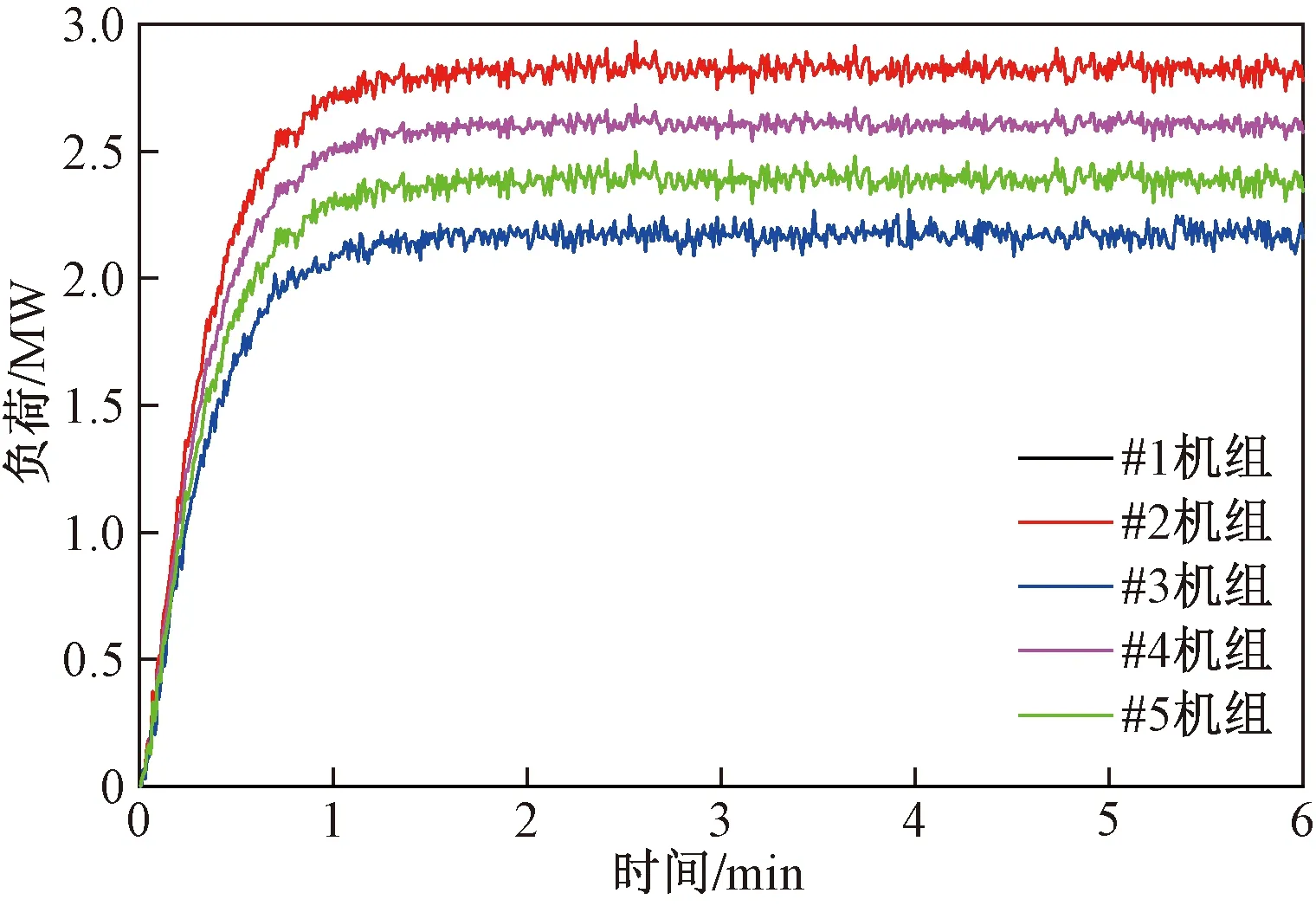
图5 机组AGC响应图Fig.5 The graph of units AGC response

各台机组的AGC指令响应如图5所示，#1机组不需要调整机组出力，由其余4台机组调整机组出力，大约需要1 min可以完成总AGC指令响应。

4.2.2 仿真案例2

当电网总AGC指令调整负荷为ΔP=100 MW，#2机组的AGC指令P2=580 MW，即机组上调容量为200、20、100、120、120 MW。首先，确定机组最大调节速率，根据式(21)分配给5台机组的AGC指令调整负荷为：11.5、25、19.2、23.1、21.2 MW。显然，#2机组的调整负荷超出限制，取机组最大可调容量ΔP2=20 MW。然后，更新ΔP并剔除#2机组，5台机组的最终分配结果为12.3、20、20.5、24.6、22.6 MW。

每台机组的响应情况如图6所示，#2机组因其自身上调容量的限制，最多可调节20 MW，在大约4 min后，可以完成总AGC指令响应。

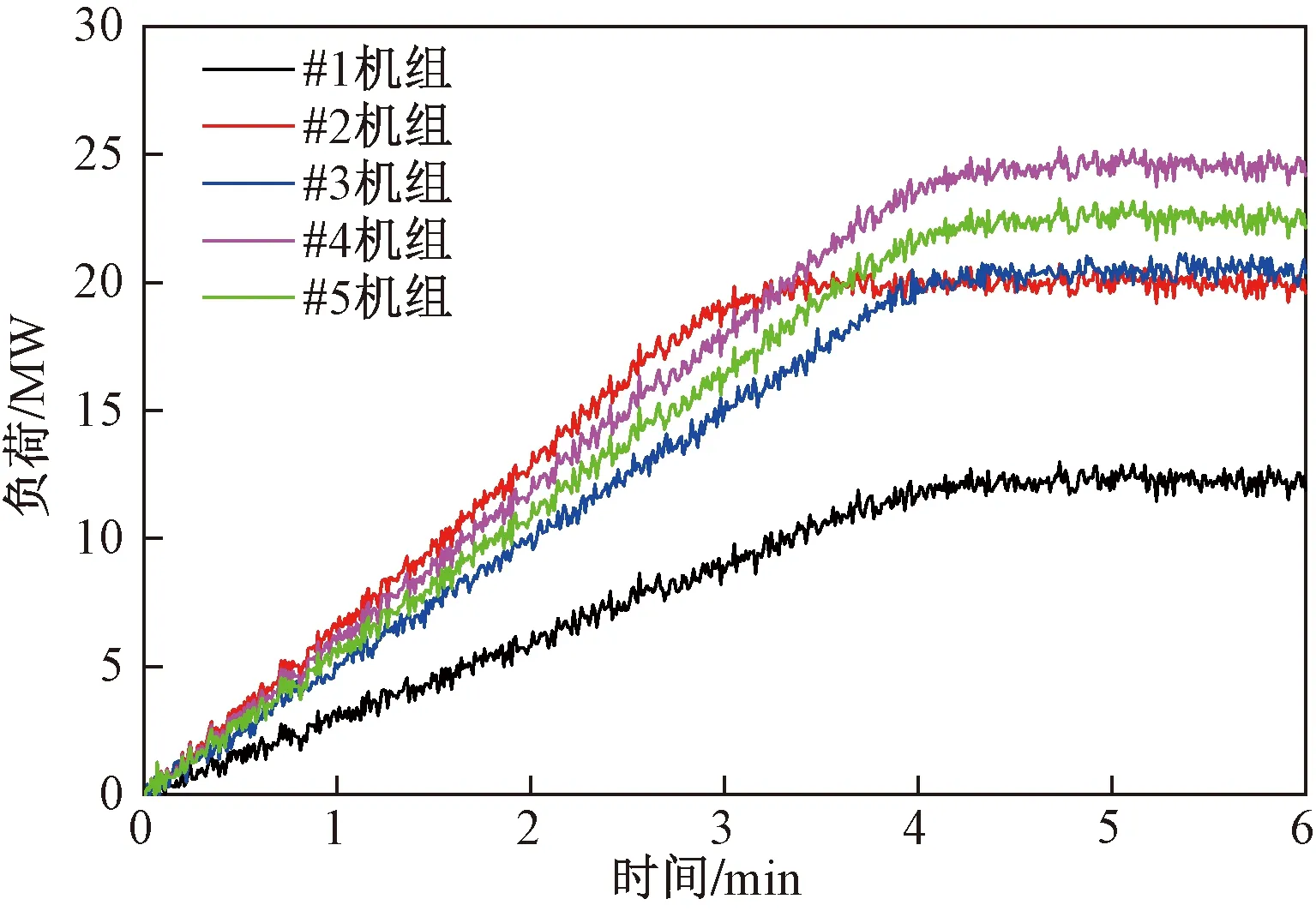
图6 机组AGC响应图Fig.6 The graph of units AGC response

4.2.3 仿真案例3

区域电网的总AGC指令调整负荷ΔP=100 MW，参与负荷调节的5台机组参数如表2所示。按照本文方法，5台机组分配的调整负荷如表3所示。各台机组AGC指令调整负荷的响应情况如图7所示，大约需要4 min可完成100 MW的AGC指令调整。

电网调度中心通常会使用平均分配法或按机组容量比例分配法对总AGC指令负荷调整量进行分配，使用平均分配法、机组容量分配法得到每台机组的调整负荷如表3所示。

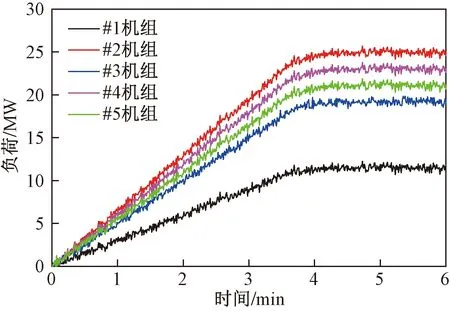
图7 机组AGC指令响应图Fig.7 The graph of units AGC response

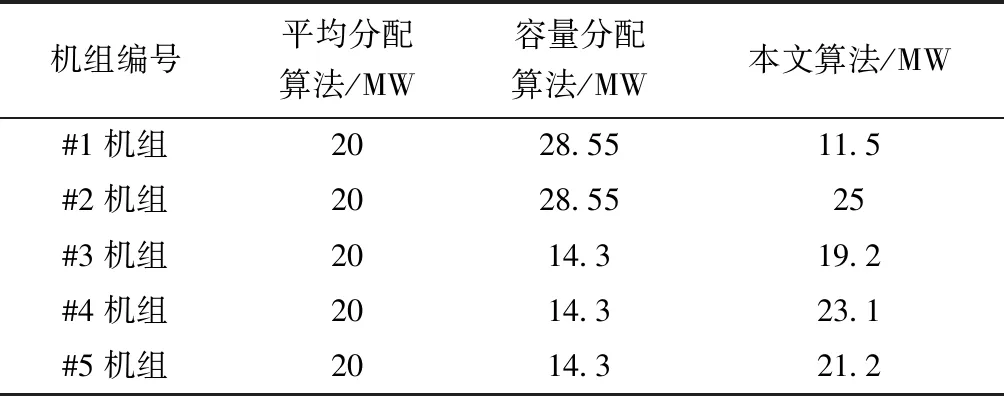
表3 3种算法的AGC分配结果Table 3 AGC dispatching results of three algorithms

整体机组对总AGC指令调整负荷的响应如图8所示，可以看出，在相同机组条件和运行状态下，当调整负荷ΔP相同时，按平均分配算法大约需要7 min完成响应；按机组容量比例分配算法大约需要9.5 min完成；按机组最大调节速率比例分配算法大约需要4 min。显然，按机组最大调节速率分配法能实现总AGC指令的快速响应。

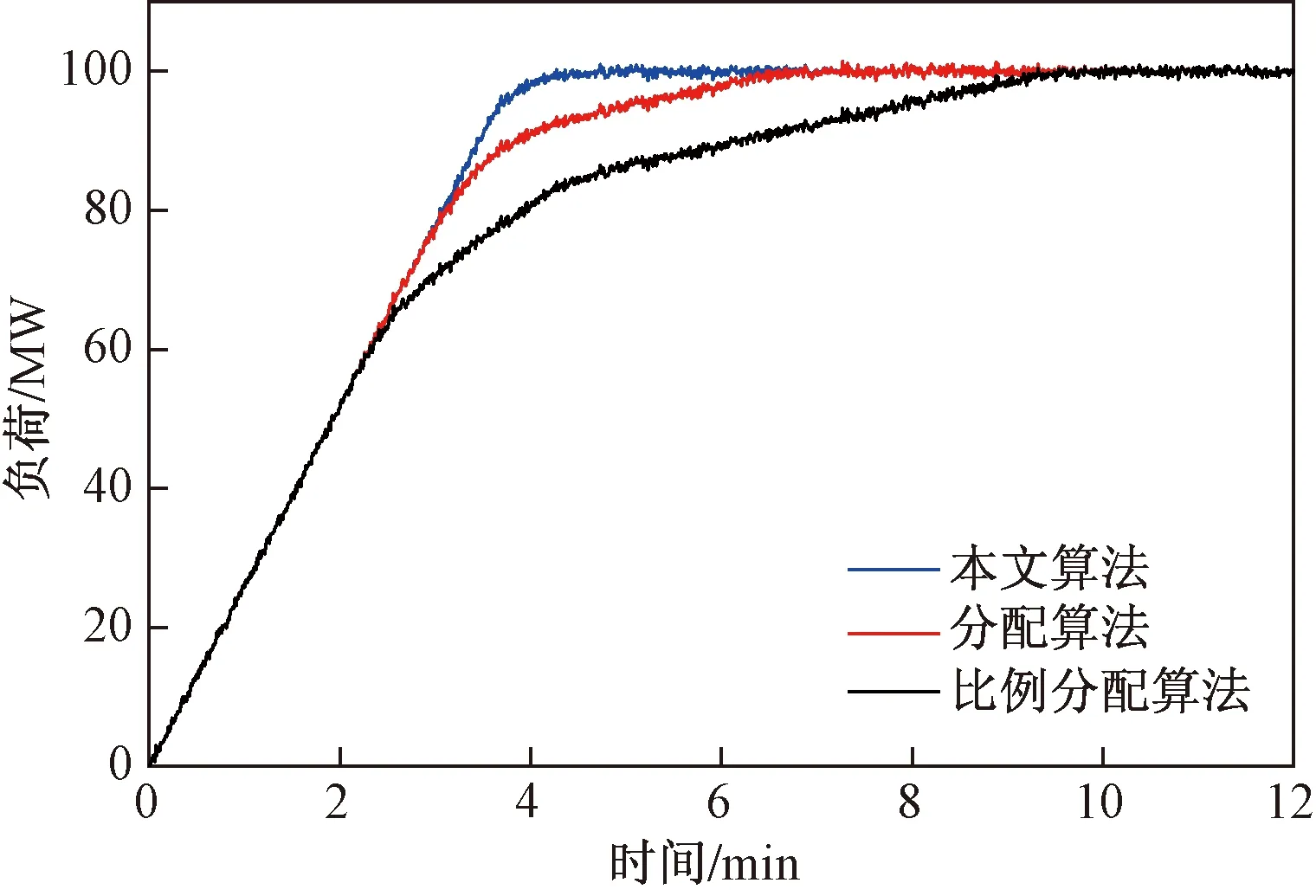
图8 机组AGC响应图Fig.8 The graph of units AGC response

5 结论

解决了电网负荷指令的调度优化问题，提出了一种基于机组最大调节速率估计的负荷指令调度方法。从机组实发功率历史数据中估计机组调节速率，基于贝叶斯估计得到机组最大调节速率的可靠估计；建立以最短调节时间为目标的优化模型，确定按机组最大调节速率比例将总AGC指令分配到每台机组；最后，通过区域模型仿真结果表明：本文算法在获取机组真实调节速率的基础上，实现了在最短调节时间内完成电网总AGC指令，有效抑制了新能源并网发电带来的电网功率偏差，达到了快速消除电网频率波动的目的。