3-SPS/PPS并联机构运动学分析

周毅钧，傅 敏，郑小东

(安徽理工大学机械工程学院，淮南 232001)

与六自由度并联机构不同，少自由度并联机构由于受到的约束增加，该类型的并联机构具有结构简单紧凑、运动平稳、承载能力大、实用性和可控性能好等优点，且少自由度并联机构可以将原本的机械机构得到相应的简化，所以少自由度并联机构得到了快速发展，研究的人员也有很多[1-5]，在工程应用方面中使用很广泛，并且并联机构也成了很多设备的核心机构，所产生的机构类型有很多，并且广泛应用于机床、微型操作、机器人、航天、液压支架等其他场合[6-9]。

空间五自由度并联机构是少自由度并联机构的一种，它可以分为三转动两平移和两转动三平移两种运动形式，例如，曹毅等[10]提出三转动两平移并联机器人机构型综合，通过理论分析了并联机构所需满足的条件以及运动性能。张东胜等[11]提出了以五自由度并联机构2-RPU/UPR为基础的混联机器人，该机构有动态响应快、运动灵活、工作范围大等特点，并通过机构的构型分析了该机构的运动学与动力学，利用数值仿真验证了机构的模型。陈修龙等[12]提出了一种4UPS/RPS并联机构，它可以实现三维转动和两维移动的五自由度运动，通过分析了机构的灵巧度综合指标，计算出并联机构的最佳结构参数，对该机构的运动学性能进行优化。

在并联机构的构造中，需要考虑所要约束的运动方向和需要实现的运动形式，以及并联机构的合理性。目前比较常用的是约束综合理论[13]和构型演变[14]两种方法。约束综合理论是通过每条支链之间的连接和运动关系，一起组合而成。由于支链可为末端的执行部分提供驱动、约束两种不同作用，所以支链可简单分为四种：无约束的主动驱动支链；恰约束的从动支链；欠约束的主动驱动支链；恰约束的主动驱动支链。构型演变的方法是在已有并联机构模型的基础上，对机构的支链数、结构参数等方面进行改进，它的变化也有很多，可以形成多种自由度的并联机构。例如，王庚祥等[15]通过以上两种方法，提出了4-SPS/CU为构型的少自由度并联机构。

现通过约束综合理论和构型演变两种分析方法，构建一种五自由度的并联机构，该机构的构型为3-SPS/PPS，它是由上平台、下平台以及四条支链组成的，其中的四条支链是三条SPS支链和一条PPS支链。该并联机构可以绕三个方向转动且可以沿两个方向移动。通过建立三维结构模型分析3-SPS/PPS并联机构的特点，计算求解并联机构的位置表达式，并且利用ADAMS仿真软件进行机构运动学仿真。

1 3-SPS/PPS并联机构的构型

将已有的6-SPS结构改变为3-SPS结构形式，机构的自由度数目没有发生变化，只是支链数由六条变成了三条，然后增加一条中间支链，且该支链恰好可以约束掉一个多余的自由度，构成了五自由度并联机构。

该机构的构型过程如下，其中3-SPS机构的运动螺旋系的标准基为

(1)

根据并联机构运动的特点，需要在3-SPS并联机构的基础上约束一个沿X轴方向的移动自由度，根据式(1)得到五自由度运动螺旋系的标准基为

(2)

式(2)中：螺旋＄′1、＄′2和＄′3可分别看成绕X轴、Y轴和Z轴的转动副(R副)；将螺旋＄′4看成一个沿Y轴方向的移动副(P副)；将螺旋＄′5看成一个沿Z轴方向的P副，其中的三个转动副可以组成一个球面副(S副)，可以得到PPS支链，再组合三条SPS支链和上下两个平台，就构成一种新型的3-SPS/PPS并联机构。

将式(2)所示的标准螺旋系进行线性组合，可以得到其中一组五自由度运动螺旋系：

(3)

式(3)中：l1、m1、n1为第一运动副在坐标系中的位移量；r1、r2、r3、r4、r5为运动副在坐标系中转动量。

3-SPS/PPS并联机构共有四条支链，如图1所示为3-SPS/PPS并联机构的结构图。机构有三条驱动支链(SPS支链)和一条从动支链(PPS支链)共四条支链。三条驱动支链的结构都是由一个P副和两个S副所组成的，与定平台相连的是第一运动副，分别是通过三个球面副相连接，用S11、S21、S31表示；中间的运动副是第二运动副，分别是通过三个移动副连接，用P12、P22、P32表示；与动平台相连的是第三运动副，也是通过三个球面副连接，用S13、S23、S33表示；而中间的支链是由两个P副和一个S副所组成，分别用P41、P42、S43表示，PPS支链的运动副P41中心位于定平台的中心，它的轴线与运动副P42的轴线垂直，球面副S43的中心位于动平台的中心。

图1 3-SPS/PPS并联机构结构图Fig.1 3-SPS/PPS parallel mechanism structure

在3-SPS/PPS并联机构的上下两个平台上建立坐标系，方向如图2所示。O-XYZ是在定平台上建立的坐标系，p-xyz是在动平台上建立的坐标系。O点位于A1A2A3组成的三角形中心，X轴与A2A3平行，Y轴与A2A3的垂线相平行，Z轴垂直定平台向上；p点位于B1B2B3组成的三角形中心，x轴与B2B3平行，y轴与B2B3的垂线相平行，z轴垂直动平台向上。

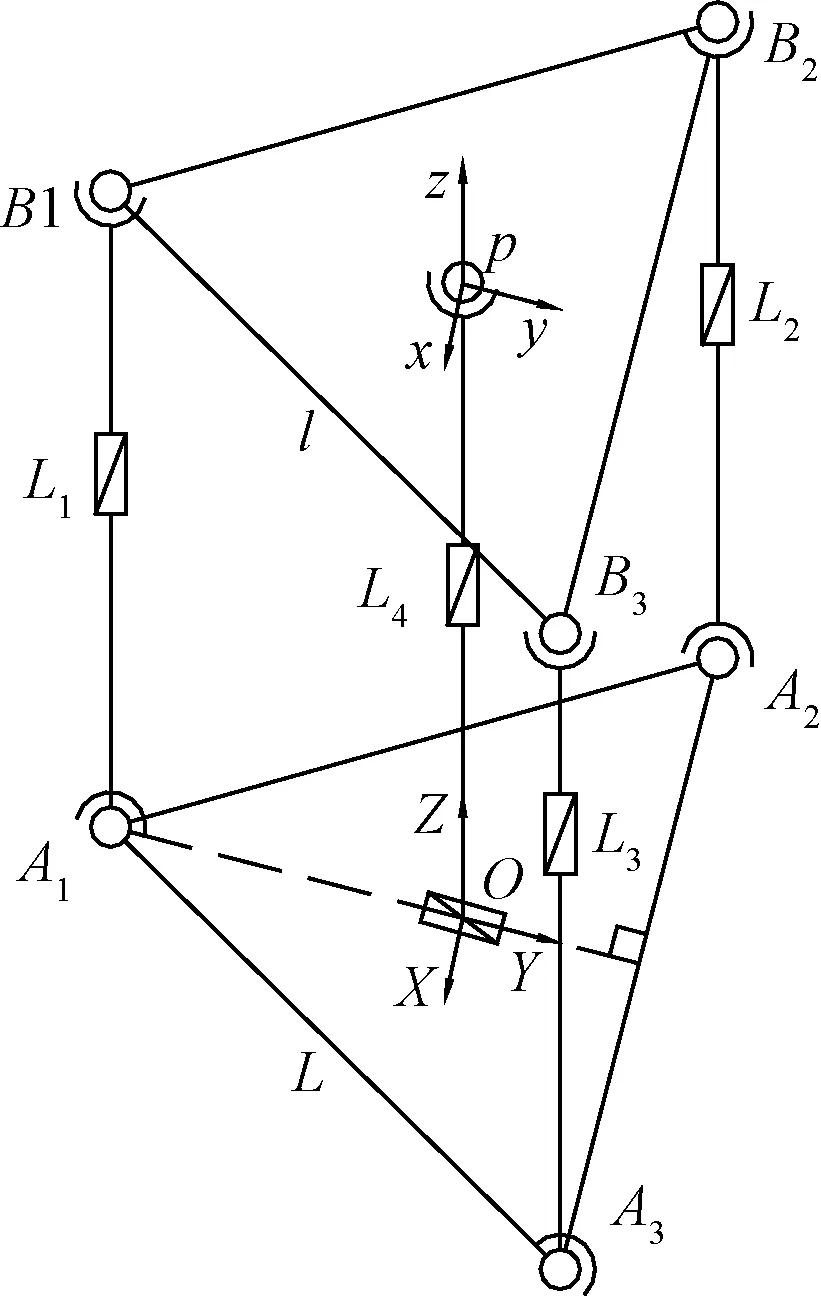
图2 3-SPS/PPS并联机构坐标系图Fig.2 3-SPS/PPS parallel mechanism coordinate system diagram

2 3-SPS/PPS并联机构的自由度分析

首先分析三条SPS支链，由于该机构三条支链的结构一致，只需考虑一条支链就可以得到三条支链的特点。根据图2所建立的O-XYZ坐标系，建立其中一条SPS支链的旋量分解图，各分量的方向如图3所示。

图3 SPS支链旋量图Fig.3 SPS branch chain spin diagram

采用螺旋理论进行计算，可以得到三条SPS支链的自由度。三条SPS支链运动旋量的表示

(4)

式(4)中:pi、qi为第一运动副在定坐标系O-XYZ中的位置；ui、vi、wi为第二运动副在定坐标系中的位置；li、mi、ni为第三运动副在定坐标系中的位置。

由式(4)可知，七个运动螺旋方程中的六个方程线性无关，所以反螺旋方程为

＄r=(LrMrNr;PrQrRr)

(5)

因为该方程组没有解，所以没有反螺旋存在，说明该螺旋系对定平台没有产生任何的约束，所以该支链的自由度数为6。

根据图2动坐标系p-xyz建立中间PPS支链的螺旋系分量，如图4所示。

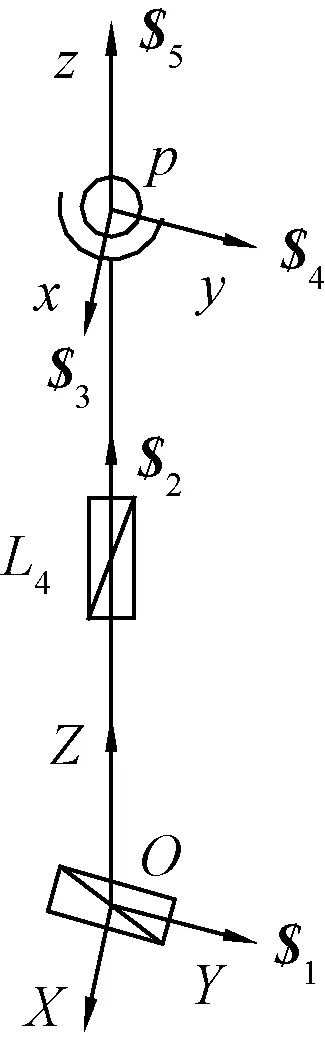
图4 PPS支链旋量图Fig.4 PPS branch chain spin diagram

根据图4的旋量示意图可以得出中间支链的运动旋量表示为

(6)

计算可得，式(6)的向量组线性无关，设此螺旋系的反螺旋系为

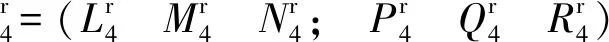
(7)

根据螺旋理论，通过式(6)可以解出一组线性无关的反旋量为

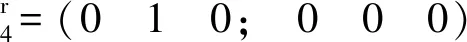
(8)

从式(8)所得的反旋量可以看出，中间的PPS支链约束了关于X轴方向的一个移动自由度，所以并联机构所有支链的反螺旋去除公共约束后的反螺旋数目和最大无关组分别为t=1、k=1，冗余约束数目根据公式v=t-k=0。

根据3-SPS/PPS并联机构整体来看，每条SPS支链都存在一个局部自由度，所以机构的局部自由度ξ=3。按照修正后的G-K公式计算并联机构的自由度[16]得

M=6×(10-12+1)+26-3=0

(9)

所以该并联机构的自由度数为5。它的动平台能实现空间三转动两移动的运动。

3 3-SPS/PPS并联机构的运动分析

3.1 3-SPS/PPS并联机构的位置分析

根据图2所示的3-SPS/PPS并联机构，机构的位置逆解就是根据各构件的结构参数以及动平台上的位姿参数，进而求解出并联机构每条驱动支链的位移长度。

假设3-SPS/PPS并联机构定平台和动平台分别是边长为L、l所组成的正三角形，图5所示为该机构初始位置时的俯视图。

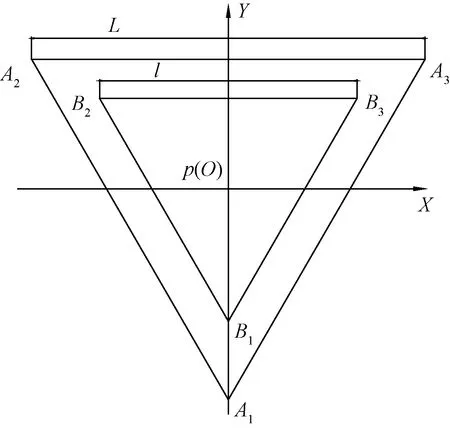
图5 3-SPS/PPS并联机构俯视图Fig.5 Top view of 3-SPS/PPS parallel mechanism

设(y,z,α,β,γ)为动平台上坐标系p-xyz相对于定平台参考坐标系O-XYZ的位移和转角。因为动平台在空间上只能作三维转动和沿Y轴、Z轴的平移运动，因此可得X=0；由A点在O-XYZ参考坐标系中的位置，Ai点的坐标可以表示为Ai=[AiXAiYAiZ]T；根据B点在p-xyz动坐标系中的位置，Bi点的坐标可以表示为Bi=[BiXBiYBiZ]T。

则动平台和定平台上各点的坐标为

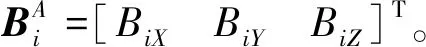
[BiXBiYBiZ]T=T[BixBiyBiz]T

(10)

式(10)中：T是余弦矩阵，而且

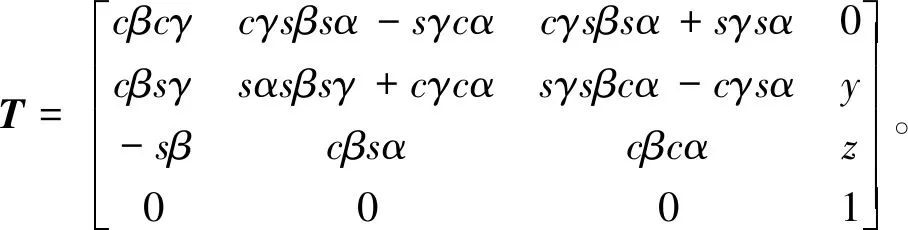
式中：矩阵T中的c代表cos函数；s代表sin函数。

当并联机构的结构参数一定时，已知动平台上的位置参数，并且通过式(10)可以求出动平台上B点坐标转换后的参数值，再根据并联机构上每个点的坐标值，可以得出3-SPS/PPS并联机构的位置反解的方程，即

(11)

式(11)中：M=cαsγ-cγsαsβ；N=cαsγ+sαsβsγ；Li(i=1,2,3)为驱动支链的位移长度。

并联机构的位置反解与正解是对立的，因此并联机构的位置正解就是通过3个输入杆的位移长度L1、L2、L3，求解并联机构动平台上的位置参数(y,z,α,β,γ)。

3.2 3-SPS/PPS并联机构的速度分析

根据上述分析，该并联机构的SPS支链为机构的驱动支链，把它作为广义输入可以记为L=[L1L2L3]T；动平台上的广义输出记为φ=[yzαβγ]T；移动副的广义输入速度表达为L′=[L′1L′2L′3]T；动平台上的广义输出速度表达为φ′=[y′z′α′β′γ′]T。

根据式(11)的方程对时间t求导数，可以得到3-SPS/PPS并联机构的速度逆解为

L′=J′φ

(12)

式(12)中：

矩阵J为系数矩阵，其中的各个元素都可以通过求导计算出，如果矩阵J为满秩矩阵时，得到并联机构的速度正解为

φ′=J-1L′

(13)

3.3 3-SPS/PPS并联机构的加速度分析

根据3.2节并联机构速度分析，则并联机构移动副的广义输入加速度表达为L″=[L″1L″2L″3]T；动平台上广义输出加速度记为φ″=[y″z″α″β″γ″]T。

根据式(12)再对时间t求导数，可得

L″=J″φ+J′φ′

(14)

如果J-1为非奇异矩阵，可得

φ″=J-1′+J-1L″

(15)

通过式(14)和式(15)可以求解出并联机构的加速度正解和逆解。

4 3-SPS/PPS并联机构的仿真分析

4.1 3-SPS/PPS并联机构的逆解仿真

由于ADAMS软件建立并联机构的三维模型比较复杂，因此使用建模软件SolidWorks来建立3-SPS/PPS并联机构的三维模型，并另存为Parasolid(*.x_t)的文件格式，然后把建好的机构模型导入到ADAMS软件中，如图6所示。

3-SPS/PPS并联机构的初始位置是动平台中心与定平台中心重合，通过ADAMS软件里面模块进行设置，首先在物体模块对机构的材料属性等设置，在连接模块对并联机构的运动进行连接，然后通过驱动模块设置驱动函数，在这里选择动平台的中心点处，驱动选择为一般驱动，各个参数的函数设置如式(16)所示。

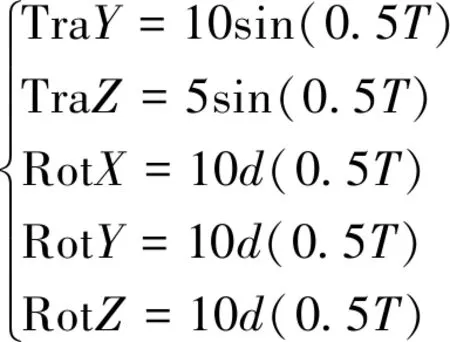
(16)

式(16)中：T为时间，s；d为弧度，rad。

在设计模块设置测量参数，然后在仿真模块设置机构运动的时间为20 s，步长为200，最后可以得到3-SPS/PPS并联机构驱动杆的位移变化范围，通过后处理模块显示曲线图，如图7所示。

图6 3-SPS/PPS并联机构模型Fig.6 3-SPS/PPS parallel mechanism model

图7 位移曲线变化图Fig.7 Change curve of displacement curve

从图7中可以看出，曲线1、2、3分别表示驱动杆L1、L2、L3位移长度的变化，都有随着周期变化的规律，杆的位移长度没有明显的突变，验证了它的正确性。

4.2 3-SPS/PPS并联机构的正解仿真

根据图6所示的并联机构模型，在驱动模块中对驱动方式和驱动位置进行修改，由3-SPS/PPS并联机构的驱动副是移动副，所以在机构的驱动副上添加驱动函数，函数设置为：50sin(πT)。

运动仿真的时间设置为10 s，步长为200，通过仿真得到了3-SPS/PPS并联机构动平台运动的位移曲线、速度曲线、加速度曲线分别如图8～图10所示。

图8 动平台位移曲线Fig.8 Moving platform displacement curve

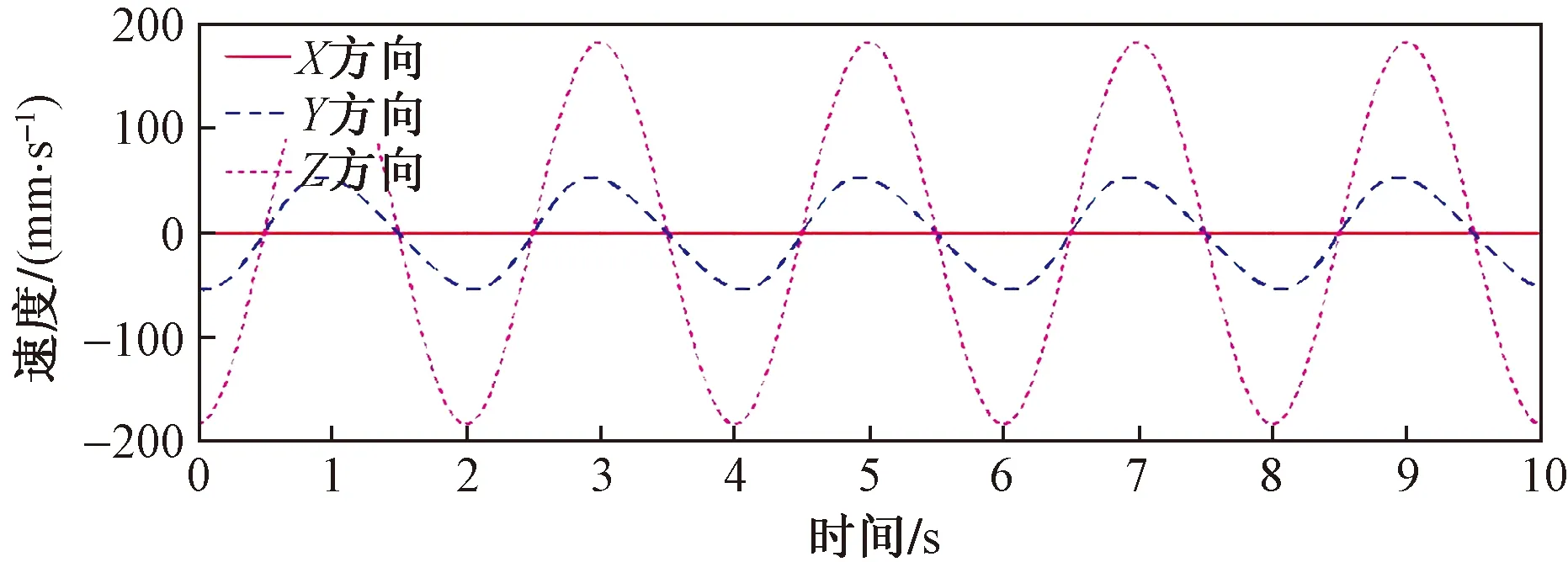
图9 动平台速度曲线Fig.9 Moving platform speed curve

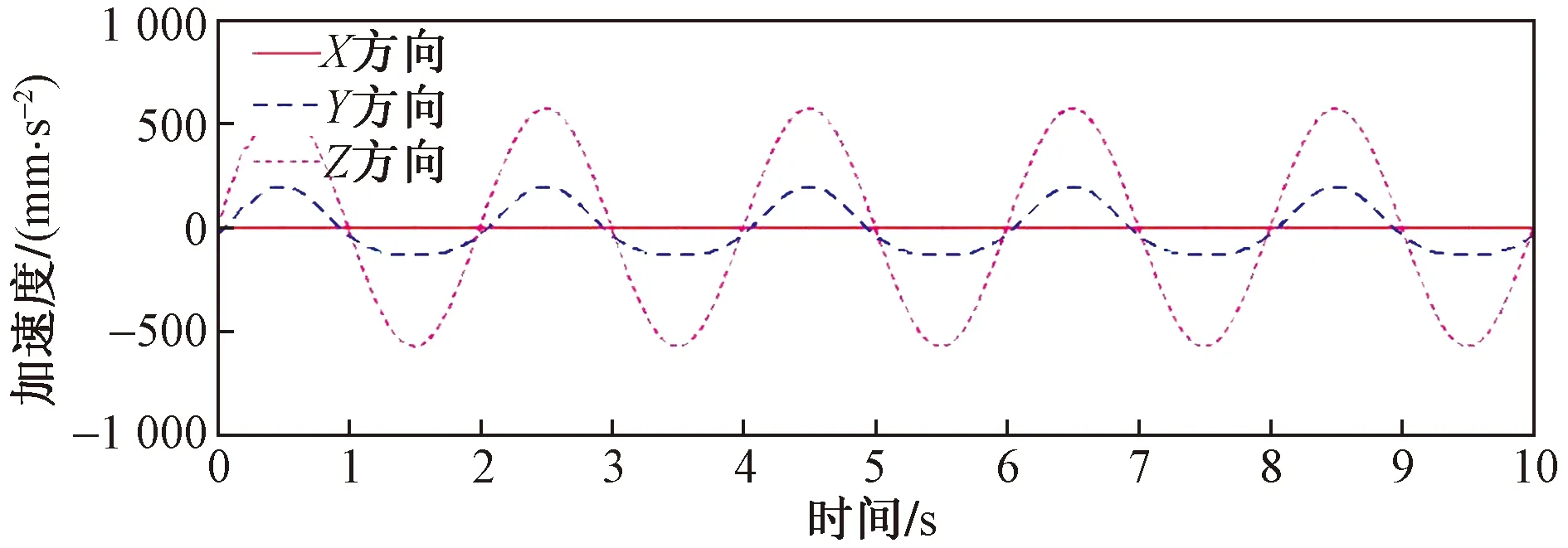
图10 动平台加速度曲线Fig.10 Acceleration curve of moving platform

由图8～图10可以看出，坐标轴x、y、z方向的曲线都很平滑，而且3-SPS/PPS并联机构的加速度曲线只有在运动仿真开始的时候出现一个很小的突变，随后也呈现规律性的、周期性的变化。

5 结论

(1)通过构型综合和恰约束原理的方法，对并联机构进行演变，得到了一种三转动两平移的五自由度并联机构。

(2)结合3-SPS/PPS并联机构的特征，通过螺旋理论分析了机构的自由度，计算求解了并联机构的位置方程表达式。

(3)运用SolidWorks软件建立3-SPS/PPS并联机构的三维模型，并通过ADAMS软件对机构进行运动平台的仿真分析，得出了并联机构的运动学模型，仿真的结果与原理分析基本一致，验证了并联机构在运动学方面的可行性，为并联机构的应用提供了理论参考。