数学期望在工业企业经济决策中的应用

张 娜，郝子硕

（1.佳木斯大学理学院，黑龙江 佳木斯 154007；2.佳木斯大学机械工程学院，黑龙江 佳木斯 154007）

1.引言

近年来，随着社会的不断发展，我国整体经济水平出现了明显的提高。在经济发展的过程中，工业企业起到了至关重要的推动性意义。经济决策是工业企业经营期间最重要的一项工作，会直接决定企业的经营状态与发展效益。在经济决策中引入数学期，望能够大大提高经济结构的安全性，降低风险。

2.数学期望与工业企业经济决策之间的关系

首先，数学期望能够提高企业在经济决策中的高效性。客观来说，由于社会环境的多变复杂，当前我国工业领域企业的竞争压力逐渐提高。面对复杂多面对社会背景，企业在进行经济决策时也很容易会陷入迷茫状态，造成较大的风险。其次，数学期望能够提高企业在经济决策中的科学性。随着社会的不断发展以及理念的不断更替，当代大众对于客观事物所存在的认知已逐渐出现了更新状态。数学可以辅助大众保持冷静客观的状态，提高在实践以及决策中的科学性，精准性。很多工业企业的管理者在分析问题时会下意识地应用感性思维，在进行某项经济决策时，也会由于思维的影响而出现问题。

3.数学期望在工业企业经济决策中的应用步骤

3.1 确定决策目标

经济决策是一项综合性比较强的活动，并且会对整个企业的经济发展与项目效益产生直接的影响。对此，需要受到工作人员的高度关注。在进行经济决策时，明确具体的决策目标是工作人员需要开展的首要工作。只有目标明确，工作人员才能够有计划，有方向地开展后续操作，并为整体工作打下良好基础。工作人员需要站在科学的角度上，综合分析经济决策项目中的潜在风险与客观因素，保证特定条件与有效资源可达到项目推进条件的前提下，明确目标，根据目标创设后续方案[1]。

3.2 计算影响概率

在进行经济决策时，企业管理者会收到很多不同的备选方案。为了保证决策的有效性，降低决策风险，管理人员需要客观冷静分析这些方案，找出彼此之间存在的差异以及各方案中所存在的可控因素与不可控因素。在确定好这些基本条件后，其还需要借用数学期望对这些因素可能会出现的概率加以计算综合考量，为下一步的分析工作奠定基本保障。

3.3 计算预期收益

在确定好各项影响因素可能会出现的概率之后，管理人员需要重新分析备选方案，并站在统计学的角度上，利用数学期望对不同方案的预期收益以及预期风险加以合理计算预测，确保所获得的收益值与相应概率之间能够达到统一状态。

4.数学期望在工业企业经济决策中的应用策略

4.1 在最佳生产批量决策中应用

最佳生产批量指的是工业企业在进行生产工作时所能够达到的成本最低，效率最高的综合生产批量。一般来说，工业企业所进行的生产工作规模相对较大，所涉及到的批次也相对较多，如果没有一个经济合理的决策方案以及决策目标，很容易会造成成本浪费、效益损失的问题。所以，企业方面需要选择最佳生产批量方案，以此降低生产成本，提高经济利润，而在该项工作中，数学期望可达到较高的应用价值。

例1：某工业企业正在进行2021 年的生产量决策。现阶段，企业工作人员已将历年的生产资料与市场销售报告收集到了一起，通过有效的分析与预测，明确了2021 年的市场销路概率。按照差中好的标准将其划分为0.2、0.5 以及0.3。并且工作人员按照生产批量规模将其划分为大中小。整体市场销路状况与生产批量如下表所示。

结合数学期望分析来看，三种不同批量所形成的预期利润分别如下。

按照相同计算方式，B 生产批量的预期利润为43，C 生产批量的预期利润为37。三者之间相互比对，利润最大的为B生产批量。

通过这一方式，工作人员能够直接了解利润最高的生产批量，从而有效加强工作效益。

4.2 在投资决策中应用

4.2.1 机械更新应用

在工业企业运营的过程中，机械设备是其中必不可少的一种工具，也是企业发展的基本物质基础。机械设备大多具有固定的使用年限，为了保证整体的生产质量，推动企业的长期发展，企业方面需要定期做好机械设备的更新。但由于机械设备规模较大，专业应用性较强，所以在更新阶段会产生较大的投资成本，需要企业做好有效的投资决策。管理人员可适当引入数学期望，利用数学期望对投资中的不可见因素与可预见因素展开有效分析，综合获取最适合的决策方案[2]。

例2：某工业企业决定替换一批新型机械设备。负责该项工作的人员通过深入市场，确定了两种不同的设备。在对设备长期产生进行分析以及检验的过程中，明确AB 设备的次品产生概率，具体如下表所示。

A 设备概率

B 设备概率

结合数学期望分析上述数据，可知A 设备的次品率为0.7，B 设备的次品率为0.6，次品率越低的方案效益越高，所以在此次经济决策中，企业方面应该选择B 设备。

4.2.2 机械故障的解决

科技发展日新月异，更多工业企业已经步入全面机械化生产阶段。在企业的投资和生产阶段，需要将机械故障问题考虑其中，并将故障出现之后损失情况计算出来，保证在特定时间之内能够达到对应利润值，上述目标的实现可利用数学期望加以解决。

例3：某企业的工厂当中一台机器运行过程故障发生概率0.2，若此类机械故障发生，那么可导致全厂停工，如果一个星期(按照5 天计算)，机械不发生故障，那么该企业能够获得10 万元利润；故障出现一次，那么可获5 万元利润；如果故障出现两次；企业不盈利也不亏损，故障超过三次，企业就会亏损2 万元；可利用企业一周数学期望计算出利润。

那么该工厂的期望利润计算如下：

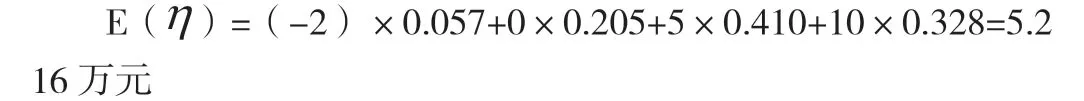
4.2.3 最佳进货量确认

对于工业企业来讲，无论是计划生产，还是制定决策，都和数学期望息息相关。针对企业进货量确认问题，就可利用数学期望，分析最大利润值。若某工业企业在月初计划储存特定商品，数量y 个，该商品每售出一个，就能获取c 元利润，若该商品当月难以售出，那么就会亏损e 元，如果该商品市场需求量属于不确定变量ε，趋近均匀分布，公式为：

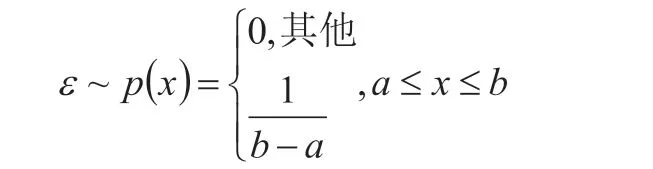
那么该企业需要在月初储存多少该商品，才能获取最高利润？

对于此问题展开分析，如果该企业存储商品数量y 个，利润可用如下公式表示

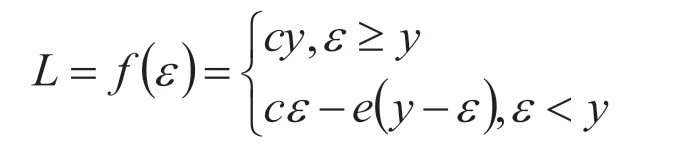
例5：假设某企业销售一种商品，该商品市场需求量为x，取值在100～300 之间，若该商品进货时间在月初进行，并且每月只进行一次进货。企业销售此商品一个的利润500 元。如果销售期间出现供过于求的现象，需要进行打折处理，那么一个商品亏损100 元；若销售期间出现供不应求的现象，可从其他企业进行调货，那么销售一件该商品可获得300 元利润。那么如何做好进货数量的确认，才能使得企业获得最高利润？求出最高利润期望？

对于此案例展开分析，因为商品需求量x 属于不确定值，也就是随机变量，处于区100～300 区间范围之内并且均匀分布，销售该商品利润y 为商品数量x 的函数，本案例当中也将其视为随机变量。由于题目涉及最高利润属于数学期望，也就是平均利润最高值。所以在求解过程，可先将y 与x 二者之间函数关系先行确认，之后将y 期望值计算出来，使用极值思想寻找期望最高值。求解过程可以假设企业月初进货量为a 个，那么可列出函数：

y=500+300(x-a)，当x ≥时，y=28a+300x；

y=5x-100(a-x)，当x ＜a 时，y=600x-100；

通过上述计算过程可以看出，该企业每月初进货233 个，能够获取最高利润，利润期望93333 元。可见,通过数学期望还能对于企业进货投资方案的确定提供辅助作用。

5.结语

综上所述，本文主要以数学期望为核心要点，通过分析其与工业企业经济决策之间的关系以及应用策略的方式，明确其具体的应用价值。在工业企业经济决策中，数学期望的应用能够大大提高整体工作的安全性，对此工作人员需要正确看待数学期望的应用价值，并能够将其融入到经济决策的整体步骤中。