Appell 函数和Humbert 函数的积分表达

王晓霞,袁学颖

(上海大学理学院, 上海 200444)

近年来, Brychkov 等[1-4]研究了双变量超几何级数函数的积分表达式, 如Appell 函数的积分表达式

另外, Saad[5]建立了Gordon 积分以及相关的恒等式; Sascha 等[6]建立了一系列超几何级数的积分表达式. 受到这些已有结果的启发, 本工作建立了一些关于双变量超几何函数的积分表达式, 包括Appell 函数和Humbert 函数的积分表达式.

为了论文的完整性, 本工作给出了Bailey[7]和Slater[8]提出的一般超几何函数的定义:

这里, 所有的参数属于复数域, 分母参数为非负正整数, 关于一般超几何函数pFq更多的性质和应用可以参考文献[7, 9]. 复数a的n次升阶乘(a)n为

式中: Γ 函数[10]的定义为

与Γ 函数关系密切的Beta 函数[10]定义为

接下来, 给出Srivastava 等[11]提出的双变量超几何函数的定义为

式中: 所有的参数属于复数域, 分母参数为非负正整数;An表示序列(A1,A2,··· ,An), 以及((Aa))n= (A1)n(A2)n ···(Aa)n[11]. 本工作所研究的双变量超几何函数及一般超几何函数都是在其一致收敛的情况下讨论的.

双变量超几何函数在超几何函数领域中具有重要的研究意义, 其中著名的Appell 函数[12]定义为

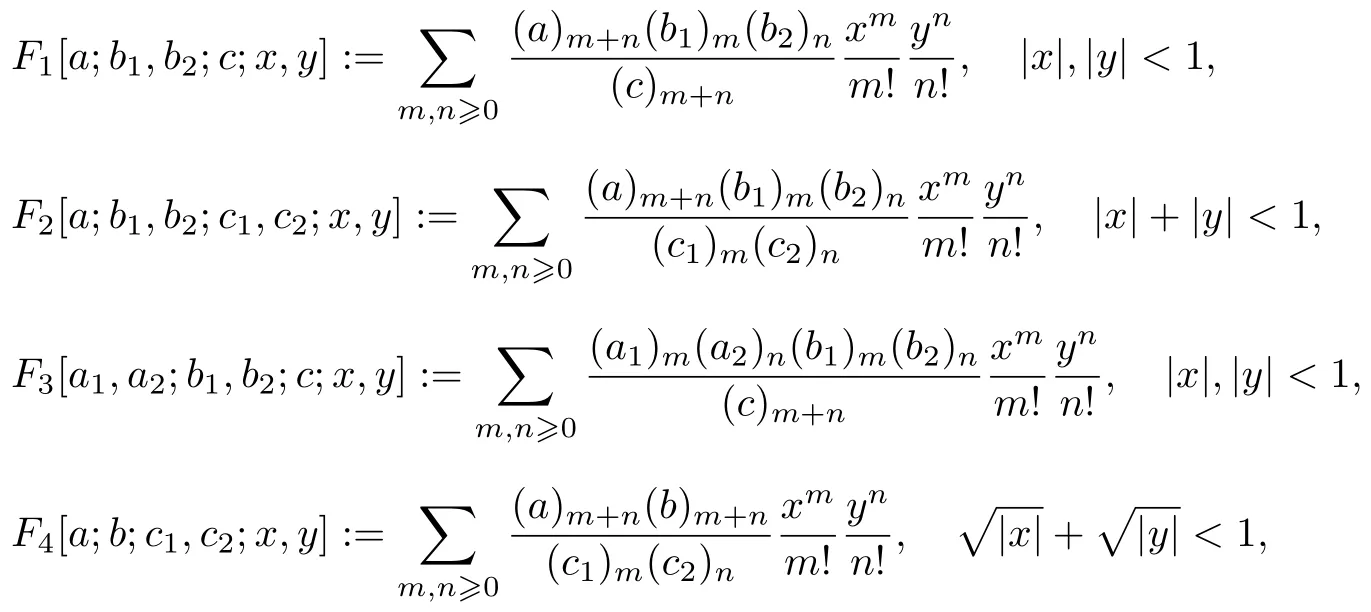
同样具有重要研究意义的Humbert 函数[13]包含

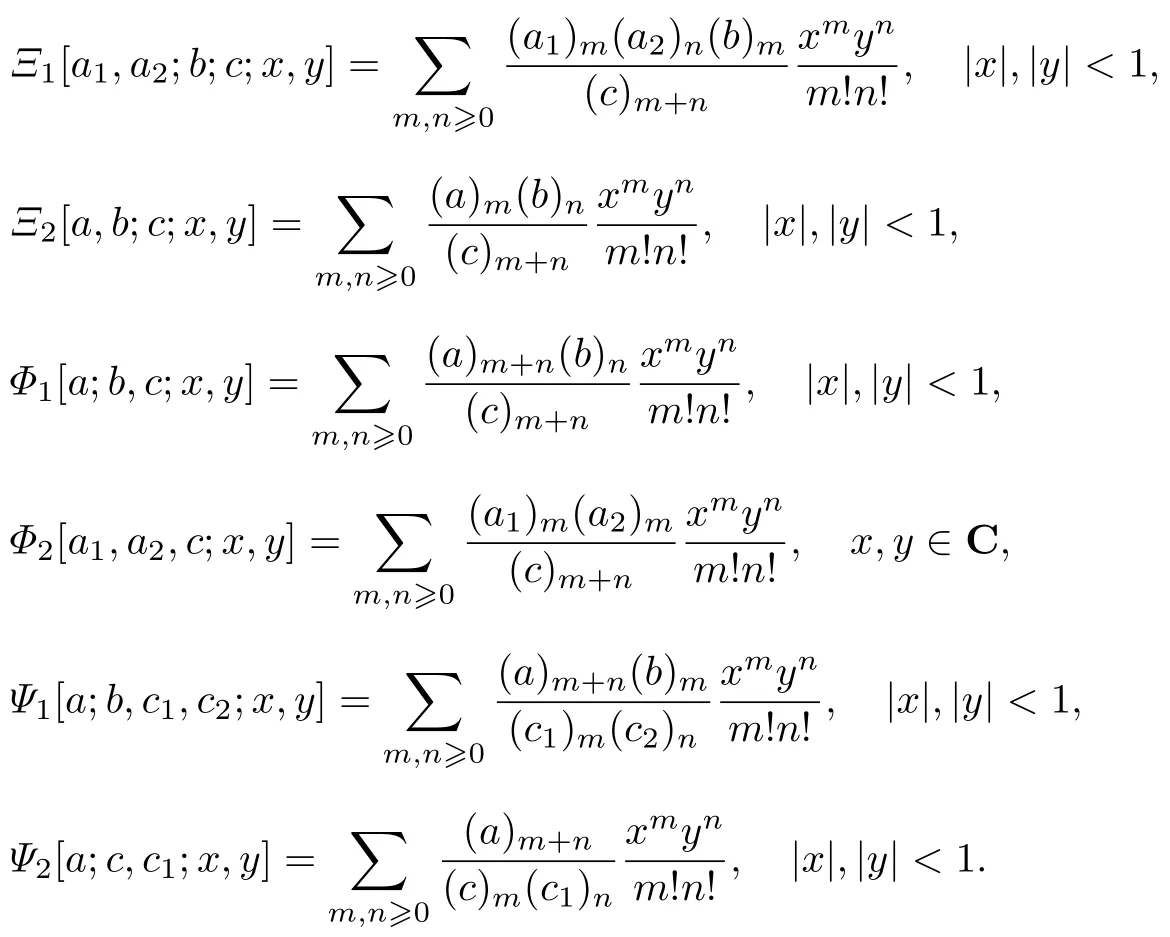
1 双变量超几何函数积分表达

借助Γ 函数和Beta 函数的定义, 本工作将给出对双变量超几何函数积分的表达式. 适当选择定理中的参数, 可以得到Appell 函数和Humbert 函数的积分表达式.

定理1下面的积分表达式是正确的:

证明 这里只证明式(1), 式(2)可同理证明. 根据双变量超几何函数的定义, 式(1)的左边形式可以表示为

这里, 认定上式中的双变量求和式是一致收敛的, 则可改变上式中求和运算与积分运算的顺序, 可以很容易地得到

令u/w →t, 根据Beta 函数的定义, 得到

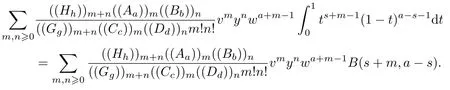
经过整理, 可以得到式(1)的右边形式, 证毕.

适当地选择定理1 中的参数, 可以得到Appell 和Humbert 函数的积分表达式.

例1 (Appell 函数的积分表达式)

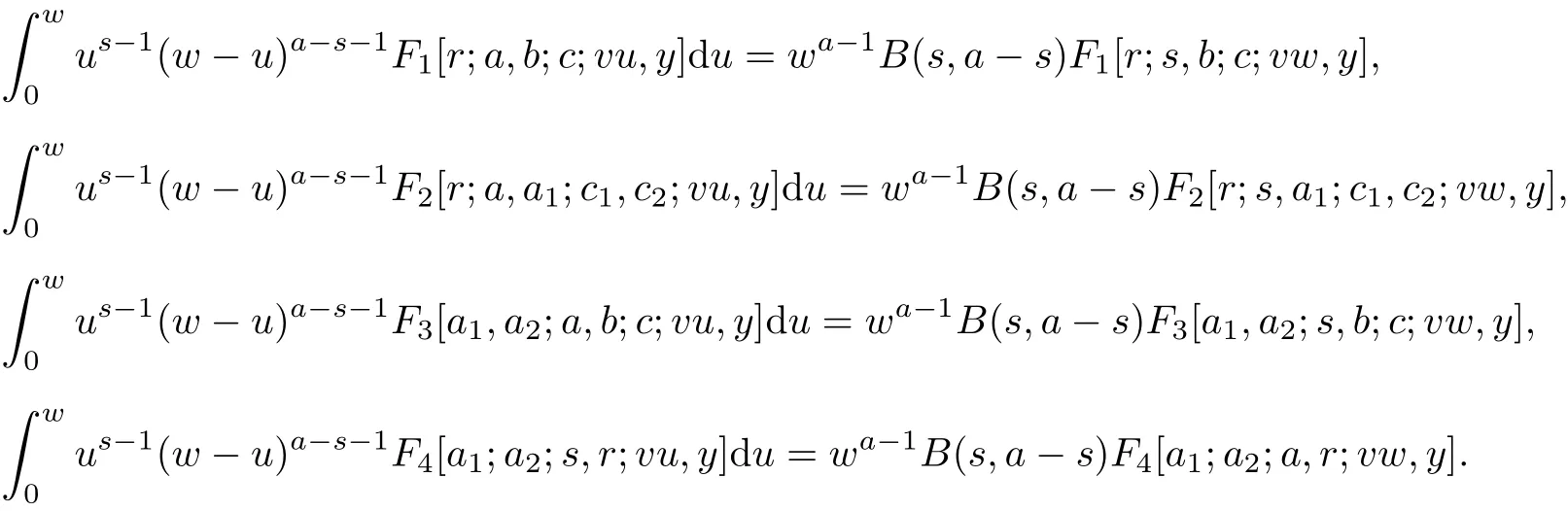
Brychkov 等在文献[1-4]已经给出这4 个积分表达式.

例2 (Humbert 函数的积分表达式)

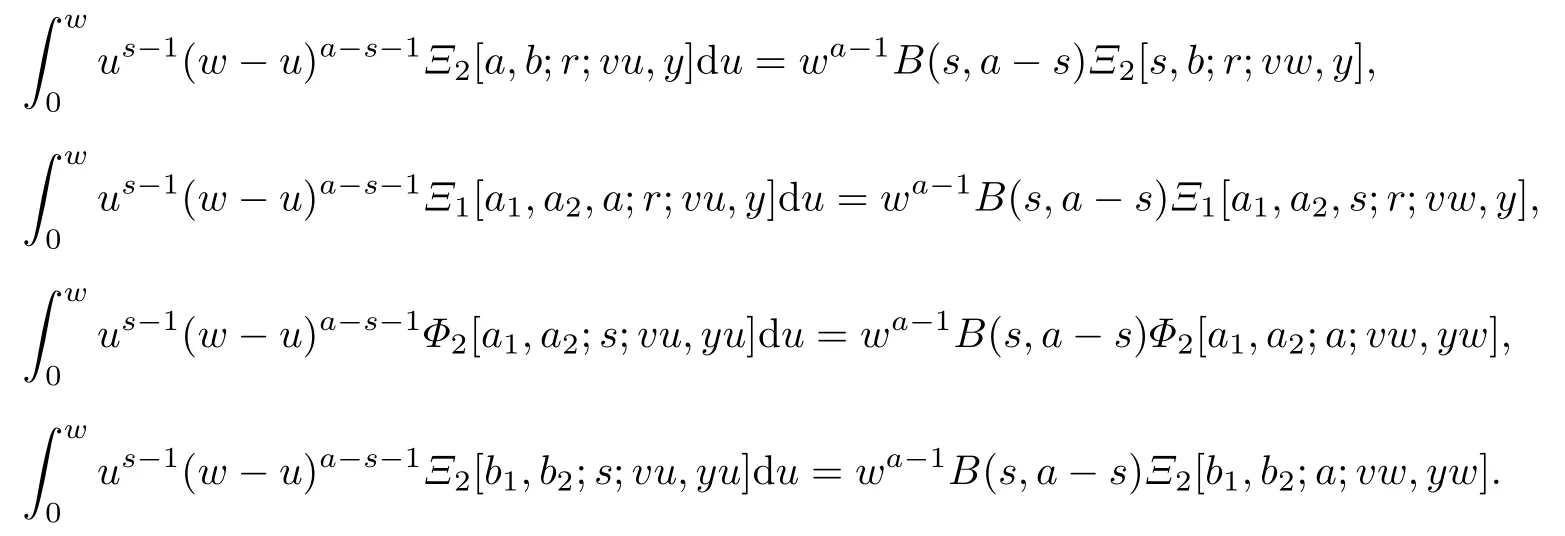
定理2下面的积分表达式是正确的:

证明 利用双变量超几何函数的定义, 式(3)的左边形式为

根据Beta 函数的定义, 得到

经过整理, 即可得到式(3)的右边形式, 同理可证式(4), 证毕.

给定定理2 中的参数, 就可以得到Appell 函数的积分表达式.

例3 (Appell 函数的积分表达式)

根据Beta 函数的定义, 还可以得到如下定理.

定理3下面的积分表达式是正确的:

证明 这里, 认定式(5)中的双变量求和式是一致收敛的, 根据双变量超几何函数的定义,式(5)的左边形式为

通过变量代换cu/w →t以及Beta 函数的定义, 可得

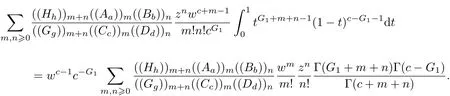
经过整理可以得到式(5)的右边形式, 证毕.

从定理3 出发, 得到了Appell 函数和Humbert 函数的积分表达式.

例5 (Appell 函数的积分表达式)

定理4下面的积分表达式是正确的:

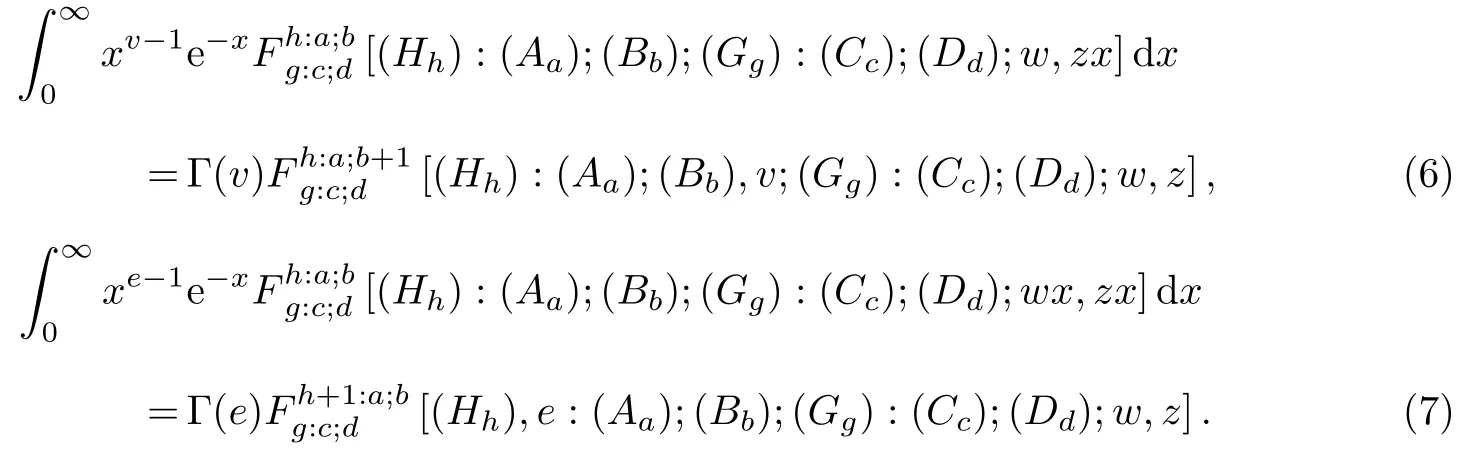
证明 此处给出式(6)的证明, 式(7)同理可证. 这里, 认定上式中的双变量求和式是一致收敛的, 根据双变量超几何函数的定义, 式(6)的左边形式为

根据Γ 函数的定义, 可得

经过整理, 可以得到式(6)的左边, 证毕.

关于定理4, 这里给出Appell 函数和Humbert 函数的积分表达式.

例7 (Appell函数的积分表达式)

在定理4 中选择合适的参数, 还可以得到Humbert 函数的积分表达式.

例8 (Humbert 函数的积分表达式)

除了Appell 和Humbert 函数的积分表达式外, 上述4 个定理还可以得到其他结果.

2 一般超几何级数积分表达

定理5下面的积分表达式是正确的:

证明 根据一般超几何函数的定义, 式(8)的左边形式为

这里, 认定式(8)中的单变量求和式是一致收敛的, 可改变上式中求和运算与积分运算的顺序,并令px →t, 得到

然后, 上述式子可以简化为

经过整理, 得出式(8)的右边形式, 证毕.

将定理5 中的参数进行特殊化, 可以得到下面几个积分表达式.

“凡有血气，皆有争心”暗示“争”是伴随血气之生而来的一种本能冲动，是“六志”不得协调的结果。而“六志”经由礼乐文化的疏导和满足才可能达致协调，当“变法”活动成为春秋后期的一股潮流之时，叔向、蔡史墨及仲尼这样一些深谙礼乐精神的贤人已经指出，那些改变礼乐传统所塑造的社会形态的改革活动，将不可避免地导向“锥刀之末，将尽争之”的乱境。礼与争的对立关系，或许在“受天地之中以生”的人群中有其根源。这一认识构成了荀子礼论的重要基础。

例9 (Humbert 函数的积分表达式)

借助著名的Euler 求和定理, 本研究建立了其他双变量超几何函数的积分表达式.

定理6下面的积分表达式是正确的:

证明 这里仅给出式(9)的证明, 同理可证其他3 个公式. 认定上式中的单变量求和式是一致收敛的, 根据一般超几何函数pFq的定义, 式(9)左边形式为

上述公式中, 本工作运用了Euler 求和定理[8]

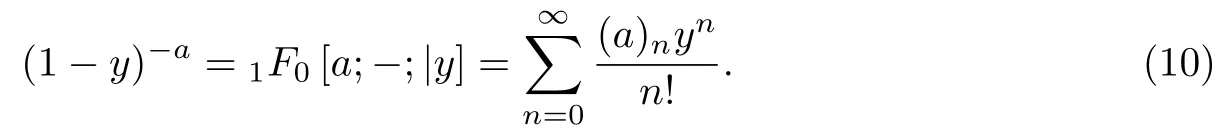
式(9)得证.

适当地选择定理6 的参数, 给出Appell 函数与Humbert 函数的积分表达式.

例10 (Appell 函数与Humbert 函数的积分表达式)

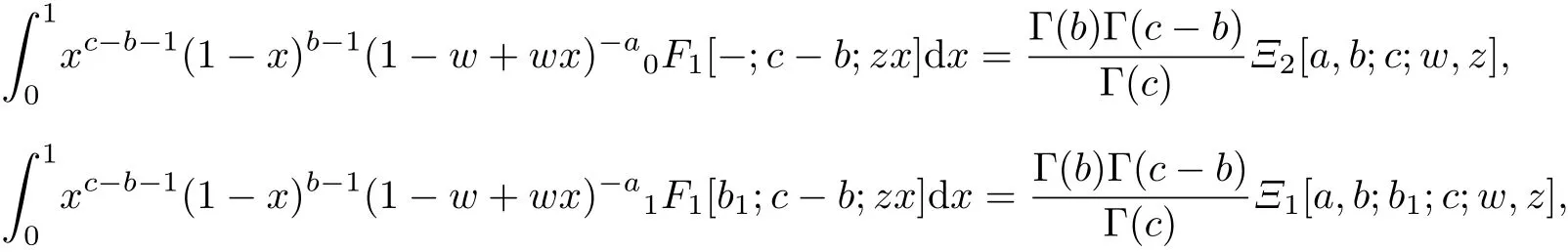
根据Gauss 求和式(12), 本工作建立了双变量超几何级数的积分表达式.

定理7下面的积分表达式是正确的:

证明 根据一般超几何函数的定义, Euler 求和定理(见式(10))和Guass 求和公式[12]

将式(11)的左边形式简化为

经过整理, 得到式(11)的右边形式, 证毕.

适当选择定理7 中的参数, 可以得到Appell 函数的积分表达式.

例11 (Appell 函数的积分表达式)

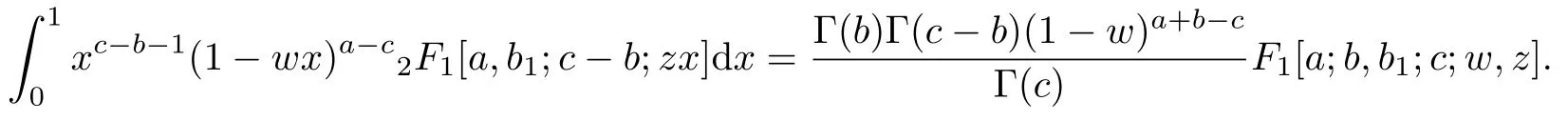
Brychkov 等[1]已经研究了这个积分表达式. 接下来, 通过泰勒展开式(15), 可以建立定理8 中的双变量超几何函数的积分表达式.

定理8下面的积分表达式是正确的:

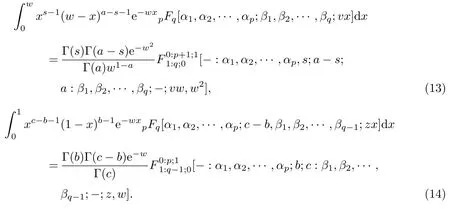
证明 下面仅证明式(13), 同理可证式(14). 这里, 认定上式中的单变量求和式是一致收敛的, 根据一般超几何函数的定义, 式(13)的左边形式为

根据ex的泰勒展开式[10], 即

得到

经过整理, 得到式(13)的右边形式, 证毕.

从定理8 出发, 给出以Φ2和1函数为例的积分表达式.

例12 (Φ2和1函数的积分表达式)